M. R. Pinheiro
IICSE University Delaware, Australia
Correspondence to: M. R. Pinheiro, IICSE University Delaware, Australia.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper is about The Barber Paradox. It mentions a bit of the history of the problem, places it in the context of the Russell’s Paradox and describes it mathematically. There is a brief discussion on three of the most interesting solutions presented so far: one from St. Thomas and two from Conway. While St. Thomas says that the barber is another person when shaving himself, Conway presents Venn diagrams to make his points come across. St. Thomas’ solution is proven not to be a solution using Conway’s argument, originally written to support it. Conway’s solutions are explained from Conway’s perspective. Were they sound, they would have come attached to a linguistic description of the problem that is purely mathematical and therefore out of human reality, what makes the problem not be a popular paradox anymore, but a purely mathematical problem instead. It is then changing the nature of the problem and therefore it is not good. Notwithstanding, we prove that Conway’s solutions can only fit a universe in which the mathematical elements have been misused and are therefore not actual solutions. A new solution, which fixes the issues presented with Conway’s studies involving the Venn Diagram, is then presented. It involves refining the current linguistic description of the problem and fixing its mathematical descriptions.
Keywords:
Barber, Russell, Paradox, Logic, Solution, Conway, St. Thomas
Cite this paper: M. R. Pinheiro, On Four Solutions to the Barber Paradox, International Journal of Advances in Philosophy, Vol. 6 No. 1, 2024, pp. 8-13. doi: 10.5923/j.ap.20240601.03.
1. Introduction
Quine would have written (Conway 1962, p. 161):“Catastrophe may lurk. . . in the most innocent-seeming paradox. More than once in history the discovery of paradox has been the occasion for major reconstruction at the foundations of thought. For some decades, indeed, studies of the foundations of mathematics have been confounded and greatly stimulated by confrontation with two paradoxes, one propounded by Bertrand Russell in 1901 and the other by Kurt Godel in 1931.As a first step onto this dangerous ground, let us consider another paradox [the article having been opened by the relatively facile paradox of Frederic in The Pirate of Penzance, who, because he was born on February 29, turns out, after 21 years, to be “a little boy of five”] : that of the village barber. This is not Russell’s great paradox of 1901, to which we shall come, but a lesser one that Russell attributed to an unnamed source in 1918.In a certain village there is a man, so the paradox runs, who is a barber; this barber shaves all and only those men in the village who do not shave themselves. Query: Does The Barber shave himself?” To understand what is involved in this problem, we first need to understand what is involved in any paradox:“For Quine, a paradox is an apparently successful argument having as its conclusion a statement or proposition that seems obviously false or absurd” (Lycan 2010, p. 615).The Barber Paradox then arises because we may reason like this: if The Barber shaves himself, then he is not shaven by The Barber, but The Barber is himself, contradiction (or absurdity)! On the other hand, if The Barber does not shave himself, then he is shaven by The Barber, but The Barber is himself, contradiction (or absurdity)!In this paper, we discuss The Barber and propose a new solution to it. In Development, we discuss three solutions to The Barber: two of them proposed by Conway and one of them proposed by St. Thomas. We prove that all three are equivocated. We then propose our own solution. In Conclusion, we summarize the article and its findings.
2. Development
Mathematical Shape of The Russell’s and The BarberRaclavsky (2014, p. 271) explains that The Russell’s Paradox is there to challenge the Comprehension Axiom. The Comprehension Axiom says that it is always possible to find a set of individuals satisfying a given condition/predicate (Raclavsky 2014, p. 271): 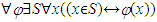 The condition given for the Russell’s Paradox is that the set cannot belong to itself, that is, we want to form a collection of sets S such that S does not belong to itself or, in mathematical language (Raclavsky 2014, p. 271):
The condition given for the Russell’s Paradox is that the set cannot belong to itself, that is, we want to form a collection of sets S such that S does not belong to itself or, in mathematical language (Raclavsky 2014, p. 271): 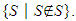 Comprehension Axiom applied to this condition,
Comprehension Axiom applied to this condition, 
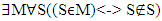 | (1) |
We cannot really find this set because if the set belongs to itself, MϵM, but the implication with arrow to the right then tells us that M then obeys the condition. The problem is that the condition is that M∉M, contradiction! On the other hand, if the set doesn’t belong to itself, M∉M, we can rewrite this as negation of the consequent of the implication with arrow to the left, what implies that the antecedent is also negated, and therefore MϵM, contradiction!Some people connect The Barber with The Russell’s. They think the paradoxes are similar. Raclavsky states: “The Barber Paradox is often introduced as a popular version of Russell’s Paradox” (Raclavsky 2014, p. 269). In mathematical symbols, The Barber could read (Raclavsky 2014, p. 272):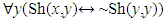 , where x is freeThe symbols mean that for all individuals, who we call y, x will shave the individual if and only if it is not true that the individual shaves themselves. It is missing saying that x is The Barber, not free. The correct mathematical description of what Raclavsky was trying to say is:
, where x is freeThe symbols mean that for all individuals, who we call y, x will shave the individual if and only if it is not true that the individual shaves themselves. It is missing saying that x is The Barber, not free. The correct mathematical description of what Raclavsky was trying to say is: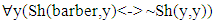 | (2) |
where y and The Barber live in the designated village, there is only one barber in the village, who we call barber here, and living in the village means satisfying a few criteria, including being there for more than three months.y=barber -> Sh(barber,barber) or ~Sh(barber,barber).a) Sh(barber,barber) -> ~[~ Sh(barber,barber)] (double negation)The negation of the consequent leads to the negation of the antecedent in the implication to the right in (2), so that it is true that ~ Sh(barber,barber) but the premise was Sh(barber,barber), so contradiction! b) ~Sh(barber,barber) implies antecedent of implication to the left being true in (2) and therefore implies that the consequent of the same implication is true and therefore what comes before the arrow to the left is verified, so Sh(barber,barber), contradiction again!We could also write The Barber in a way to make it look more similar to the mathematical description of The Russell’s Paradox (1):φ=doesn’t shave himself, S=individual who lives in the village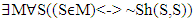 | (3) |
Therefore there is a set M, which we can describe as the set of those who are shaven by The Barber, such that for all Ss, each of them an inhabitant of the village, S belongs to M if and only if S does not shave himself. The similarities between The Russell’s and The Barber stop by there: the mathematical symbols that may be used to describe the problem. Philosophically, these problems are very different: the main issue in The Russell’s is that we ask about the inclusion of a set that is not yet formed in a set that is its alternative mathematical description, but the main issue in The Barber is that we ask about the inclusion of an individual who is fully formed in a set that is not a mathematical description of this individual. The Russell’s has to do with time of formation of a set, since the set under analysis has not yet been formed when the central question to the problem is asked. For more on this, consult (Pinheiro 2012) and (Pinheiro 2016), but The Barber has nothing to do with time of formation of the set. Yet the time issue is the core of all trouble in the Russell’s, so that these paradoxes are not really, philosophically speaking, similar to each other, even though they may be told to resemble each other when it comes to their mathematical descriptions. Discussion of Three Solutions to The Barber (Conway’s Solutions)We now come back to the linguistic interpretation of the mathematical description of The Barber we mentioned before, in this very paper, which we will prove, later on, is equivocated: “Therefore there is a set M, which we can describe as the set of those who are shaven by The Barber, such that for all Ss, each of them an inhabitant of the village, S belongs to M if and only if S does not shave himself.” Now, does The Barber belong to this set?If he does, he lives in the village, so that he is an S, and does not shave himself, so that he belongs to M and M is the set of those who will be shaven by The Barber, who is himself, contradiction! If he doesn’t, he shaves himself or he doesn’t inhabit the village. If he shaves himself, M is the set of all those from the village who are shaven by The Barber, and he is The Barber, so that he has to belong to M, contradiction! He cannot not inhabit the village because of (2), but observe that, if he doesn’t inhabit the village, there is no paradox.Conway (1962, pp. 163-166) tells us that St. Thomas proposes that the barber who shaves himself and the teacher who teaches himself are in the same situation, that of not being a teacher or a barber per se at that moment, of doing it (teaching or shaving) to themselves. Instead, they would be a teacher and a barber per accidens when doing that (teaching or shaving) to themselves.That does not solve the paradox because even though we can say that who shaves themselves is not the barber, but the barber per accidens instead, barber is the same person as barber per accidens and therefore we still end up with the contradiction. Conway (1962, pp. 163-166) solves this by saying that there is no contradiction and it is just our equivocated way of interpreting things, the scarcity of linguistic terms and so on. His reasoning seems to work well for the case in which we talk about professions, but not people, since the physical identity of the barber per se and the barber per accidens is still the same, even though the profession might be seen as different, and the paradox is about that, not their profession by the moment of shaving or being shaven. Conway then comes up with an illustration using the Venn Diagram, which is supposed to be a proof that the barber from The Barber does not shave at all or is shaven by a barber that comes from another location (Conway 1962, p. 166): | Figure 1 |
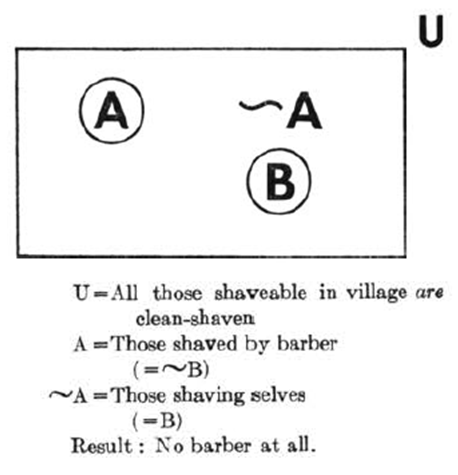 | Figure 2 |
Obs.: Please notice that it is missing saying ‘in the village’ after clean-shaven in the Figure 1’s description.Call the only barber in our village Mike, just for the sake of putting the problem more real.With the Figure 1, we have that Mike can be in A, B or U-(AUB). If he is in B, he shaves himself. Since he is The Barber, he would have to be in A as well. However, A and B are disjoints, so that there is nobody in the intersection and therefore that is not possible. If he is in A, he is shaven by himself and therefore should also be in B. Again the same problem. In this case, he can only be in U-(AUB) and therefore he is never shaven, says Conway (pp. 166-167). Notice that if Mike does not live in the village, there is no conflict and the root of this solution is that A and B are disjoints, so that, if we prove that that is not the case, this solution is proven to be incorrect as well. On the other hand, if Mike is bearded, he doesn’t shave himself and lives in the village, so that he HAS to be shaven by The Barber, since otherwise we are disobeying the conditions of the problem, and he then has to be shaven by himself and therefore he cannot be bearded. Besides, observe that one of the conditions of the problem is that Mike lives in the village (2).With the Figure 2, we have that Mike can be in A, B or U-(AUB). If he shaves himself, he is in B. Since he is then shaven by The Barber, he is also in A, what is impossible because A and B are disjoints. If he is shaven by The Barber, he is in A. Since The Barber is himself, he also shaves himself and is in B. Again an impossibility. In this case, he can only be in U-(AUB) and therefore he was shaven by someone else, says Conway (p. 167). Conway says that they then had to have a barber from another community coming to serve them and that barber would have to shave the entire community (Conway 1962, p. 167). Our Mike then has to live outside of the village or not be The Barber. Notice that this solution is also based on the assumption that A and B are disjoints, so that, once more, if we prove that is not the case, we are also proving that this solution is incorrect. One of the conditions of the problem is that Mike lives in the village, though, and another condition is that he is the only barber in it and shaves all who don’t shave themselves, so that this solution is not actual anyway (if Mike does not live in the village, there is no paradox as well). Conway (1962) must have believed that he solved the Barber Paradox, even though that is not the idea we get about his beliefs when we read his paper. Either Mike is never shaven or he does not live in the village, according to him.Let’s then assume, for the moment being, that Conway’s solutions are sound. We then have that nobody can be happy with them for real. Deep inside, we all know that The Barber would have shaven himself, being him the only barber in the place, even though we could imagine some aberrations, such as he asks someone else, who is not a barber, to shave himself. The problem seems acceptable in the way it is proposed. It seems to us that it is just natural stating things like that even if The Barber shaves himself, so that Conway (1962) solves the paradox in a mathematical way, but the solution must then be something a bit outside of Mathematics. Conway’s solutions - and he presented two of his own therefore – are comparable to destroying the doll by splitting it into two for having been given the instruction of making two children equally happy through it. It also compares to retracting the article that is being the object of authorship dispute, solution sometimes adopted in research (Faulkes 2018, p. 2). In one case, both children are equally happy, but that just means that they are both unhappy, and in the other the public is left without the result, which could have even saved lives. It is not really good solving things like this: Injuring Mike in one of them, since he is now not allowed to live in the village and be its barber, and, in the other, inventing he never got shaven. It is worth observing here that Russell’s Paradox was also mathematically solved: one of the mathematical solutions was given by the own Russell (Pinheiro 2016, pp. 110-111). The problem with Russell’s solution to his own paradox is how unnatural it all looks philosophically and mathematically speaking, since it adds axioms to Set Theory (for more on The Russell’s and Russell’s solution, see (Pinheiro 2016)).It is maybe for noticing all this that Conway comes up with another solution, which is a mathematical interpretation of what St. Thomas said, using a Venn Diagram (Conway 1962, p. 167):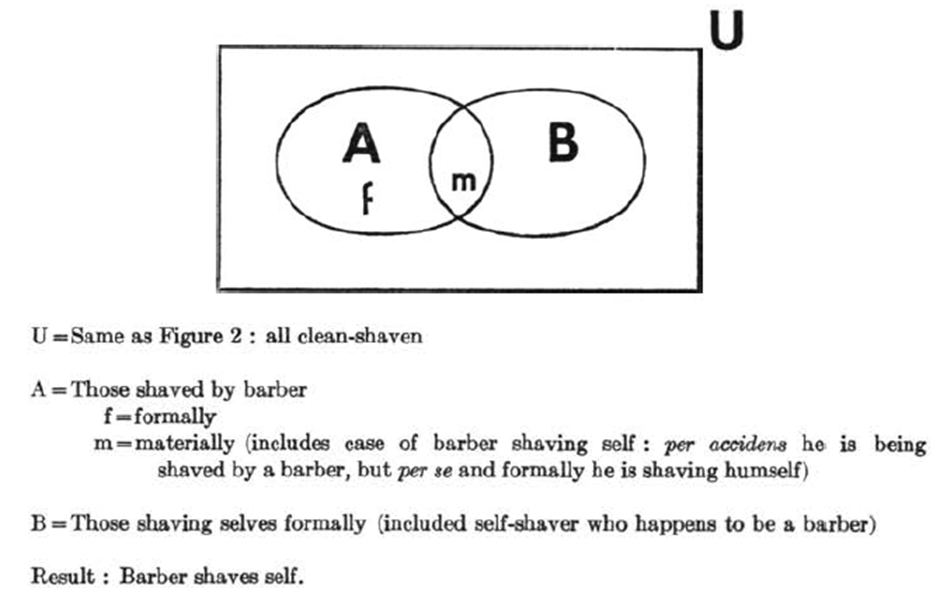 | Figure 3 |
The problem with this ‘solution’ is that we either use the rules of Mathematics or we don’t use the Venn Diagram. There cannot be any intersection between A and B, according to Conway and Figure 1, because it is said that The Barber shaves only those who don’t shave themselves. It is either the case that A and B are not disjoints or that they are such: it cannot be both, not in Mathematics, sorry, Conway. There is no such a thing as material and formal pertinence here. It is all about individuals and Mike is the same one, regardless of occupying a position of barber per se or barber per accidens. A and B are sets of people, not their professions… . According to the description of Figure 3 presented by Conway, A is not ‘those shaven by The Barber’, but ‘those shaven by The Barber materially or formally’, since the boundary of A covers both cases. He then says that B is ‘those shaving themselves formally’, so that we understand it is not materially. Yet he puts m, which can only stand for materially shaven, inside of the line marking who belongs to B, so that the diagram is not a true representation of the situation, therefore it is absolutely incorrect.We can however say that St. Thomas has tried to come up with new terms to explain the only possible reality to those not accepting it, so that he did solve the paradox but created a bit of confusion with his words. One can say that, after reading St. Thomas’ solution, we get tempted to describe things as Conway did in Figure 3.Our SolutionThe solution to this problem is reality. We need to model reality, not distortions of such. It is impossible for The Barber to shave everyone in the village all the time. There is always going to be someone who couldn’t attend the saloon, as a minimum thing (sickness, duties, work, etc.). Some would refuse to be shaven as well. Since the problem involves humans, we need to consider not those who don’t shave themselves, but those who don’t shave themselves and pay1 The Barber to shave them (still things to be considered, such as if they can afford) or are the own barber. One could still say that The Barber is sure he shaves all men in the village who don’t shave themselves. We must remember that nowadays we have women choosing ‘himself’ to refer to themselves, and being legally allowed to do that, and those don’t shave themselves, and wouldn’t be shaven by The Barber either, for the hair doesn’t grow. Well, some might choose to shave to have it growing as well, but… . We would then have to define man as being someone naturally born with a penis, and say S belongs to the set iff S is a man, lives in the village, and does not shave himself. We need to know if The Barber lives in the village, since if he does not live there there is no paradox. We want to have a paradox, we will go to the last drop of effort for that purpose, so let’s assume he does live there. We also want to make the paradox be as objective as possible, so let’s just say that The Barber shaves those who don’t shave themselves AND pay for him to shave them.If we split the set of the village people into two, one containing those who are shaven by The Barber, and another containing those who shave themselves, we have to know that The Barber may be in the intersection, since he may shave himself and, because he is The Barber, he is then going to be part of the set of those shaven by him. He cannot choose not to shave because everyone who doesn’t shave themselves is shaven by The Barber. He cannot pay someone else to shave him because it is assumed that he is the only barber in the village and all are shaven by him if shaven. In the Venn Diagram description, we would then have A and B not being disjoints with Universe being all inhabitants of the village and intersection being The Barber.We must remember, when looking at these diagrams, that it is a condition of the problem that all inhabitants who don’t shave themselves are shaven by The Barber, so that there will be nobody in U-(AUB) in Figure 4. Therefore, in Figure 4, AUB=U. AUB=U->A=U-B+(AՈB). In other words, A is the set of those who don’t shave themselves or are The Barber in Figure 4. 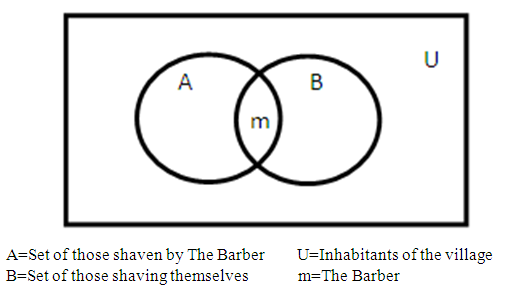 | Figure 4 |
Our solution, which is just a reading of the diagram, must then reflect this reality.The linguistic description of The Barber could then be: There is a set M, which we can describe as the set of those who are shaven by The Barber, such that for all Ss, each of them an inhabitant of the village, S belongs to M if and only if S lives in the village, is not The Barber, pays The Barber to get a shave and does not shave himself or is The Barber. Notice that we can also simplify it even more, if wanting to go closer to its original description: There is a set M, which we can describe as the set of those who are shaven by The Barber, such that for all Ss, each of them an inhabitant of the village, S belongs to M if and only if S lives in the village, is not The Barber and does not shave himself or is The Barber. The mathematical description of The Barber could then be: ∀y(Sh(Mike,y)<->(((~Sh(y,y) Λ Pay(y,Mike)) Λ y≠Mike) v y=Mike)). Now, if y is The Barber, Sh(barber,barber), no contradiction anymore.Notice that we can also simplify it even more, if wanting to go closer to its original description: ∀y(Sh(Mike,y)<->((~Sh(y,y) Λ y≠Mike) v y=Mike)).
3. Conclusions
The Barber Paradox is not a popular version of the Russell’s Paradox: both paradoxes can mathematically be described in a similar way but their philosophy is very different. The paradoxical element, for The Barber, appears in Philosophy, not in Mathematics, since, in Mathematics, all is solved. In The Russell’s, with the theory of types from the own Russell, one can say that there is still margin for doubt inside of the own Mathematics, not only in Philosophy (Pinheiro 2016): Would making changes to Set Theory be a wanted solution, we wonder? Shouldn’t we try everything that is not that before taking this radical step?Many have proposed solutions to these paradoxes in the past. The most interesting ones, in what regards The Barber, come from St. Thomas and Conway. While St. Thomas proposes that The Barber is someone else when he shaves himself, Conway uses the Venn Diagram to prove his points, one of them involving St. Thomas’ solution to The Barber. The identity of The Barber is still the same, his physical identity, so that he has to be the same in both situations, that of shaving himself and that of shaving others. That puts down St. Thomas’ solution: The Venn Diagram proves that only if B had another description the solution would be acceptable. The Venn Diagram is also used by Conway to try to prove that it is not possible to have The Barber living in the village and shaven if the rules of the problem are followed to the last dot. The Barber would have to not be shaven if The Barber lives in the village and shaves all and only those who don’t shave themselves. Notwithstanding, we proved that the rules were far from being obeyed to the last dot in his diagrams, so that he didn’t present a single actual solution to the problem in his Venn Diagram illustrations. We then proved that the Venn Diagram descriptions of the problem created by Conway are all incorrect, what means that his three solutions are not actual solutions. He forgot to mention that The Barber can shave himself and be in the set of those shaven by The Barber, so that his sets, A and B, are not really disjoints. The Barber cannot not shave because then he is shaven by The Barber, according to the conditions of the problem, and we then get contradiction. The Barber cannot be from outside of the village or not exist either because it is given that he does exist and lives in the village. It is important working on the linguistic description of the problem. We then propose that we become more realists: it would be impossible to guarantee that The Barber always shaves everyone in the village who doesn’t shave themselves. People might not be able to attend the saloon, might not have money to pay for the shave. Might dislike The Barber all of a sudden and refuse to shave with him as well. So many possibilities… .In this case, it can never be an absolute truth that The Barber always shaves everyone who doesn’t shave themselves. We have to reword this. We propose that we say that The Barber shaves everyone who pays to be shaven by him and is not himself or himself. Mathematically, this would read: ∀y(Sh(Mike,y)<->(((~Sh(y,y) Λ Pay(y,Mike)) Λ y≠Mike) v y=Mike)).Mathematics finally agrees with Language and Psychology once more and The Barber shaves himself and is also shaven by The Barber, who is himself.
Note
1. The initial proposal was ‘ask The Barber to shave them’. A reviewer pointed out that The Barber could ask himself to be shaven. That is not really something that could happen in reality apart from abnormal people, who talk to themselves. However, we then say ‘pay’ because if asking is something the reviewer sees as normal for The Barber to do, paying has to be abnormal. Nobody would expect The Barber to pay himself in reality for his own shave.
References
| [1] | Conway, P. H. (1962). The <<Barber>> Paradox. Laval Theologique et Philosophique, 18(2), 161–176. https://www.erudit.org/en/journals/ltp/1962-v18-n2-ltp0961/1020024ar.pdf. |
| [2] | Lycan, W. G. (2010). What Exactly is a Paradox? Analysis, 70(4), 615–622. https://academic.oup.com/analysis/article/70/4/615/106991. |
| [3] | Raclavsky, J. (2014). The Barber Paradox: On Its Paradoxicality and Its Relationship to Russell’s Paradox. Prolegomena, 13(2), 269–278. https://hrcak.srce.hr/file/191533. |
| [4] | Pinheiro, I. M. R. (2012). Concerning the Solution to the Russell’s Paradox. E-Logos, 20, 1-15. https://elogos.vse.cz/pdfs/elg/2012/01/21.pdf. |
| [5] | Faulkes, Z. (2018). Resolving Authorship Disputes by Mediation and Arbitration. Research Integrity and Peer Review, 3(12), 1-7. https://researchintegrityjournal.biomedcentral.com/articles/10.1186/s41073-018-0057-z. |
| [6] | Pinheiro, M. R. (2016). Russell’s Paradox, Our Solution, and the Other Solutions. International Journal of Theoretical and Applied Mathematics, 2(2), 110-114. https://www.sciencepublishinggroup.com/article/10.11648/j.ijtam.20160202.22. |



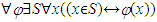 The condition given for the Russell’s Paradox is that the set cannot belong to itself, that is, we want to form a collection of sets S such that S does not belong to itself or, in mathematical language (Raclavsky 2014, p. 271):
The condition given for the Russell’s Paradox is that the set cannot belong to itself, that is, we want to form a collection of sets S such that S does not belong to itself or, in mathematical language (Raclavsky 2014, p. 271): 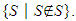 Comprehension Axiom applied to this condition,
Comprehension Axiom applied to this condition, 
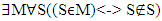
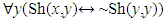 , where x is freeThe symbols mean that for all individuals, who we call y, x will shave the individual if and only if it is not true that the individual shaves themselves. It is missing saying that x is The Barber, not free. The correct mathematical description of what Raclavsky was trying to say is:
, where x is freeThe symbols mean that for all individuals, who we call y, x will shave the individual if and only if it is not true that the individual shaves themselves. It is missing saying that x is The Barber, not free. The correct mathematical description of what Raclavsky was trying to say is: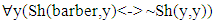
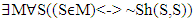




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML