1. Introduction

It is usually hard to convert what is in the language of Philosophy into the language of Mathematics since Philosophy allows for degrees of vagueness and uncertainty that Mathematics cannot tolerate.

The Sorites are part of the intersection between Mathematics and Philosophy since they involve operations, such as addition, recipes to produce inferences, such as induction, semantics, and syntax, and so on.

“The sorites paradox is the name given to a class of paradoxical arguments, also known as little-by-little arguments, which arise as a result of the indeterminacy surrounding limits of application of the predicates involved.” [1]

Soros is Greek for heap [1], so that The Sorites would be arguments involving things that are similar or equal to heaps. An example involves heaps of wheat [1]: “since one grain of wheat does not make a heap, it follows that two grains do not; and if two do not, then three do not; and so on. This reasoning leads to the absurd conclusion that no number of grains of wheat make a heap.”

A way to further illustrate the argument involved: if adding one grain of wheat to a nonheap does not make a difference, then let me add one grain per second and tell me what made us end up with an accumulation of wheat that is undeniably a heap by the end of one year.

Yet another way to further illustrate this argument: 1) Adding one grain of wheat does not make any difference; 2) There is an accumulation of n grains of wheat, where n was attained from adding grains of wheat one by one to the existing accumulation, which had initial amount of grains zero, and n is large enough to constitute a heap; 3) The accumulation of n grains of wheat must be both a heap and a nonheap of wheat.

Wheat and its grains1

Another example involves accumulation of hair ([2], p. 198):

Horatio and his baldness

A way to further illustrate the argument involved: if adding one hair to a bald man does not make a difference, then let me add one hair per second and tell me what made us end up with an accumulation of hair that means undeniably non-bald by the end of one year.

Yet another way to further illustrate this argument: 1) Adding one hair does not make any difference; 2) There is an accumulation of n hairs, where n was attained from adding hairs one by one to the existing accumulation, which had initial amount of hairs zero, and n is large enough to make us see a non-bald person; 3) The accumulation of n hairs must mean both bald and non-bald.

[3] brings the following definition of the Principle of Mathematical Induction: “If, for any statement involving a positive integer, n, the following are true:

1. The statement holds for n=1 and

2. Whenever the statement holds for n=k, it must also hold for n=k+1

then the statement holds for all positive integers, n.”

The Sorites start with a candidate to nonheap/bald that has zero grains/hairs, so, let’s call the number of grains/hairs n, the property of being a nonheap/bald P and the first element to be assigned/not the property n_1. P(n₁)=P(1)=nonheap/bald. We know that one grain/hair does not make any difference and, from there, P(n_k)->P(n_k+1) or the property nonheap/bald of the person with k hairs or of the accumulation with k grains implies the property nonheap/bald of the person with k+1 hairs or the accumulation with k+1 grains.

[4] brings the following definition for syllogism: “A syllogism is a deduction consisting of three sentences: two premises and a conclusion. Syllogistic sentences are categorical sentences involving a subject and a predicate connected by a copula (verb).”

In the above illustrations, steps 1 and 2 bring premises and step 3 brings a conclusion.

The Sorites is then deeply connected to the theories of syllogism and mathematical induction. It is just that it actually presents a structure that has not been described by Aristotle and therefore points at the incompleteness/inaccuracy of his theories or to the inadequacy of the Sorites as a logical argument and a counterexample to the mathematical induction since, as it stands at the moment, it represents its failure.

We then investigate these issues deeper. The proposed solution is that the results of Aristotle that we here study are inaccurate and The Sorites looks like a counterexample to the mathematical induction, but it is actually adding to the completeness of its justification.

The study explores from the simplest statements of The Sorites to its most elaborated presentation in terms of syllogism and mathematical induction. What justifies such exploration is the fascination of academics with the problem. Hyde once said it took him his entire life to study The Sorites (Personal communications, University of Queensland, Australia, 2000), meaning to study it properly. Our initial investigations of this problem happened at the University of Queensland in 2000 ([5], [6]²) and the results were mainly around there being a private logic to each one of us and a line that was determined by the lexicon, the lexicographers having the best solution to the problem that far. We defended that, contrary to what Hyde defended back then, which was a universal line splitting heaps from nonheaps, we had several lines, which were all fine, even if each human being had their own. We then put some algebra on The Sorites and told the same things in [7]. [8] brings a summary on our findings up to the year of 2016. The idea was always that The Sorites is a statement about how wealthy human language is when put against logic, that it is an allurement, but not a paradox or a problem. In not being a paradox or a problem, The Sorites could still be an allurement that is used as a tool to prove that there is something wrong with the mathematical induction or the Aristotelian Logic. We here prove that it is not a tool to prove that there is something wrong with the Aristotelian Logic and the mathematical induction still remains strong after being tested against it.

2. Material and Methods / Experimental Details / Methodology

The material used is scientific articles, academic encyclopedias, personal communications, academic books, and academic websites.

The methods used are systematic Bloom’s analysis of the results of the scholastic application of logical tools to relevant data sets and Bloom’s synthesis.

3. Results and Discussion

Syllogism is one of the sigmatoids [9] we use here: two premises and a conclusion.

“A syllogism is a deduction consisting of three sentences: two premises and a conclusion. Syllogistic sentences are categorical sentences involving a subject and a predicate connected by a copula (verb). These are in turn divided into four different classes: universal affirmative (a), particular affirmative (i), universal negative (e) and particular negative (o).” [4]

From [4]: “universal affirmative (a), particular affirmative (i), universal negative (e) and particular negative (o), written by Aristotle as follows:

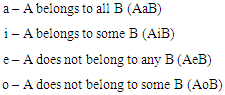The tag ‘nonheap/bald’ (A) then belongs to all accumulations of wheat/hair, B since adding one grain/hair does not make any difference and every new accumulation of wheat/hair will be the result of adding one grain/hair and we can always regress to the initial point, which is zero grains/hair. With this, AaB on the first step.

At the same time, we will unavoidably find a B that we will classify as a heap/nonbald and, with that B, many will come since it suffices adding one grain/hair to the accumulation, so that A does not belong to some B or AoB on the second step.

These premises (AaB and AoB, when put together) lead to no conclusion in Aristotelian Logic, which is summarized in [4], and therefore The Sorites is not an argument that is described in Aristotelian Logic and therefore it is not an acceptable argument in it.

Aristotle wrote: “It is impossible that the same thing can at the same time both belong and not belong to the same object and in the same respect, (…).” [10]

This is the Law of Non-Contradiction or LNC [10].

The Sorites then represents a serious flaw in Aristotelian Logic and it is a counterexample to the LNC unless we can prove that the contradictory conclusions are due to us having a ‘different respect’ instead of the ‘same respect’. AaB contradicts AoB and therefore gives an impossible result in Aristotelian Logic, for the same thing cannot belong and not belong to the same object and in the same respect.

Absolutes are difficult things to deal with if we talk about the physical perception of an individual or their private logic [7] and therefore also about the result of the efforts of the ego when having to contain the pressures of the id and the superego while passing that perception through personal filters, then selecting best decisions and actions [11].

Happiness in humans involves believing we are different from machines and therefore are freer and can choose to say heap/nonbald as we point to no wheat/no hair at all to make a joke, which would bring laughs to plenty, laughs being regarded as motivation to keep on living.

The introduction of the expression to the World of Science however brings what is exact and machine-like to the table and Science would like to reject whatever does not have that nature, of absolute exactness.

That is when we felt obliged to describe The Sorites as a universal affirmative, so, ‘all those objects are nonheaps’, because we are obliged to agree that one grain does not make a difference for all situations, so forms and shapes of nonheaps since all could be told to come from an accumulation that was one less grain from the previous one and therefore the universal negative, ‘every nonheap plus one grain is not a heap’, leads to that and a particular affirmative (this is a heap).

Notwithstanding, the human mind tends to assign a world reference [12] to a sigmatoid and stick to it to the end of a proposal, especially if the proposal is a syllogism: nobody will change the world reference in the middle of the syllogism. That is when the human mind picks the simplest case scenario for The Sorites: in the case of the grains of wheat, it will subconsciously design a horizontal accumulation since that follows from thinking of the mathematical induction and the mind immediately associates the problem to the mathematical induction. In this way, each new grain is placed sideways and in a perfect row with the previous grain, what will indeed never lead to a heap since we associate heaps to vertical accumulations, not horizontal ones. In the case of the hairs, it picks a single hole in the head and we end up with a ponytail, but nobody associates the ponytail to non-bald. That is still a bald person, however with a ponytail… .Yet, when asked to ‘shake it’, when warned therefore, the human mind will think that the heap could be formed traditional way, so vertically and each hair could be added at a distance x from the previous hair, distance possibly measured by a circumference. That is when we do have a heap and a non-bald person at a certain stage, so that it is indeed a bald and a non-bald person, a heap and a non-heap AT THE SAME TIME. In this case, the mathematical induction is fine for the case of one dimension and we have problems only with the Aristotelian Logic.

When the syllogism is rebuilt to accommodate these findings, we get

Mathematical heaps: 1) Adding one grain of wheat does not make any difference if we add it in a way to form a horizontal line with the previous grains; 2) Any accumulation of n grains of wheat, where n was attained from adding grains of wheat one by one to the existing accumulation, which had initial amount of grains zero, is a nonheap; 3) The accumulation of n grains of wheat is a nonheap of wheat.

Non-mathematical heaps: 1) Adding one grain of wheat makes a difference because, for every linear, and vertical, accumulation of grains of wheat there will be a breakage moment, when the grains will flatten up and the column will break because that other grain was added; 2) There is an accumulation of n=n₂ grains of wheat, where n was attained from adding grains of wheat one by one to the existing accumulation, which had initial amount of grains zero and n is large enough to constitute a heap; 3) The accumulation of n grains of wheat, n greater than or equal to n₂ is a heap.

Mathematical baldness: 1) Adding one hair does not make any difference if the hair is added by inserting it in the same follicle where there was a hair since a ponytail of hairs on a head still means a bald person; 2) Any accumulation of n hairs, where n was attained from adding hairs one by one to the existing accumulation by inserting them in the same follicle, which had initial amount of hairs zero, means a bald person; 3) The accumulation of n hairs means a bald person.

Non-mathematical baldness: 1) Adding one hair makes a difference if the hair is added to the circumference whose center is 1cm away from the previous circumference center and distinct from all other centers of all other circumferences already used, but still on the external surface of the head of the person; 2) There is an accumulation of n=n₂ hairs, where n was attained from adding hairs one by one to the existing accumulation, which had initial amount of hairs zero and n is large enough to constitute a non-bald person; 3) The accumulation of n hairs, n greater than or equal to n₂, means a non-bald person.

In Logic, the method of accumulation should matter, so that we now have entirely logical arguments, which can finally be addressed exclusively by Logic.

For both The Sorites of The Heap and The Sorites of the Bald, we now have:

Mathematical version: AaB in the first step. AaB in the second step. AiB in the conclusion.

Non-mathematical version: AiB in the first step. AoB in the second step. AiB in the conclusion.

These syllogisms are also not accounted for in [4], what proves that Aristotle’s Logic is incomplete or is not entirely described in [4] since it is just natural that AiB plus AiB give AiB and AaB gives BiA, which is the same as AiB according to [4]. It is also natural that if A belongs to some B and A does not belong to some B, A belong to some B.

These syllogisms are seen in Set Theory, in Mathematics, and are therefore acceptable there. Aristotle’s Logic has frequently been described in Set Theory terms, so that it is expected that these are truths also in his system. In Set Theory, The Sorites is not acceptable because also there the LNC reigns supreme.

4. Conclusions

We then have an unacceptable syllogism since it is nowhere described in [4]. Either The Sorites is a fact and therefore the Aristotelian Logic needs to be replaced with a more scientific or exact Logic, or it is possible to find some flaw with this argument.

In case the Aristotelian Logic needs replacement, we need a logical system that does not embrace LNC, such as Priest’s Logic of the Paradox, LP [13].

Human language seems to be reducing three-dimensional elements, namely a human being, and an accumulation of wheat, to one dimension in this argument, but we are then perhaps obliged to state the problem more properly: adding one grain of wheat to the tallest vertical row won’t make any difference as to the classification of the object (heap or not) or adding one grain of wheat to the longest horizontal row won’t make any difference. Notice that the latter is usually true and we could then add one grain ad infinitum in the horizontal direction without ever feeling compelled to say that is a heap since heap is usually associated with vertical growth… . In the same way, we could say adding a hair to the circumference of the circle with diameter 2mm from the previous hair added won’t make any difference and similar things.

There is no problem with the mathematical induction because when the human mind focuses on horizontal row and adding one grain in perfect alignment with the previous grains, it clearly sees that there will never be a heap. In the same way, when it focuses on a single hole in the head and adding one hair to it, it clearly sees that there is never going to be a non-bald person. It is then an issue with simply describing the problem in other terms; more mathematical and more in alignment with the definition of mathematical induction, which was made for one dimension, not for a vertical accumulation of grains or a circular distribution (as explained above) of hairs, which would have to be three-dimensional images.

The Aristotelian Logic is either only partially described in [4] or incomplete since we have found at least a couple of syllogisms that are not listed there and are acceptable. On the other hand, The Sorites is not a tool to prove it is somehow wrong because when things are told to belong, the world reference is X and, when things are told not to belong, the world reference is Y and X is different from Y. The description of Aristotle’s Logic in [4] is clearly incomplete since it does not bring LNC.

[4] tells us: “Avicenna is quick to point out that neither general nor special absolute sentences behave as expected. For example, they do not fit the traditional square of opposition. ‘Every B is A’ on the general reading does not contradict ‘Some B is not A’.” There is then no impossibility in Aristotle’s Logic for reasoning to develop in terms of symbols and the premises of The Sorites. The Aristotelian Logic is then only partially described by the symbols in [4], so that if a syllogism does not figure there it does not mean it is unacceptable in Aristotle’s Logic. Yet, LNC makes The Sorites unacceptable through Set Theory. With this, The Sorites is not a tool to produce evidence on there being something wrong with the mathematical induction, despite the initial impression, but it is an unacceptable argument in Mathematics because of Set Theory and LNC. In Philosophy, it might be possible to add it to the list of syllogisms in Aristotle’s Logic.

ACKNOWLEDGEMENTS

We would like to thank Hyde and Priest for the infinite efforts made in the year of 2000 to introduce us properly to the World of Logic and The Sorites.

Competing Interests

There are no competing interests.

Definitions, Acronyms, Abbreviations

LNC: Law of Non-Contradiction

LP: Logic of the Paradox

Notes

1. https://www.bakingbusiness.com/articles/47076-a-larger-than-expected-russian-wheat-crop-burdens-futures and https://www.southernexposure.com/api/redirects/product/2173

2. We had long discussions about this problem with both Hyde and Priest in the year of 2000 while doing our Postgraduate Diploma in Logic at the University of Queensland, this since the first semester of the course, when Hyde introduced us to the problem through one of his lectures. We also developed our theories with the help of Priest during our Special Topic with him, where he supervised us in the project A Solution to The Sorites and this was during the second semester of 2000.