1. Introduction

One could think that if we change a small rule in Classical Logic, we have a nonclassical system, even because that is what we ourselves said in a previous text (Pinheiro, 2016). Rigorously, therefore, what we are about to study here is possibly a nonclassical system. We then have to think of the difference between assessment, isolation of mistakes, and correction of mistakes (three items) and boredom, imagination, and breaking rules (another group of three items): Perhaps Classical Logic is not as perfect as we initially thought it was.

If we do have mistakes, we’d better fix those.

There is what we would like to call theoretical utility of a concept and what we would like to call material utility: In theory, everything is useful, even a single letter in isolation. We are sure some people could spend even an entire life talking about the beauty of a letter in isolation. In practice, the theory is another, as they say everywhere on earth.

Drawing a line to split what is application from what isn’t is something very difficult to do: In 2001, Doctor Dragomir asked us to find applications for S-convexity. We did not hesitate: The faculty where we worked was an Engineering faculty. We simply went around explaining what it was and asking if they could imagine some utility.

What he actually meant, he would later on clarify, was applying the concept of S-convexity to Inequalities, what obviously made immediate sense to us as soon as he said it.

It is applying the concept, no doubts about it, but we still saw that as Pure Mathematics, since it is all inside of Pure Mathematics in our Inner Reality (Pinheiro, 2016a). Coming from Brazil, we do expect Applied Mathematics to be something like foam that dissolves in the environment in record time, what they once produced at UNICAMP.

When we apply things inside of the same piece of Science, is that an application or an attempt to further investigate how the phenomenon we refer to behaves?

We tend to think it is the latter.

When we think of Classical Logic, a piece devised by very respectable researchers, as for all we know about them so far, people like Frege, we immediately think of Mathematics.

At the same time, we never really stopped to think about how we apply Classical Logic inside of Mathematics until we saw the work of Doctor Corcoran, we now realize: Our proofs, those we print so proudly in our books, never ever respected the principle of explosion or the (0,0) or the (0,1) match in the material implication.

We always say that if we get a contradiction, we have proved that our assumptions are equivocated. If we start by assuming that X is true, for instance, and we get to the end of our mathematical proof, and, as a conclusion, we find out that X is false, we decide that X is not true, and therefore that X can only be false.

What we have actually done here was applying the rules from Classical Logic and reaching a contradiction after producing some inferences.

We get that X is true and we get that X is false in the example given. Since Classical Logic says that contradictions imply all possible assertions in the system (Explosion Law), we get the Ex Falso Quodlibet principle (as Hyde would put it: Falsity spreads).

(Berto, 2009)

We can see Classical Logic as our CSTJ¹ Biology professor saw human beings (moving conglomerates of molecules, like she said she actually saw that after studying the discipline for that long), and therefore as a conglomerate of 0s and 1s plus connectors, or we can see Classical Logic as Doctor Corcoran sees it: It is applicable to real life.

That is what tells us if we are from Pure or Applied Mathematics, we reckon.

The reaction of every pure mathematician to the World of Corcoran would probably be the reaction we had: Oh, dear, why bother?

It is only when we lose prejudice against the Actual World that we can see that he might be right in one or two of his points.

We say that Classical Logic is the logical system we use to build the own Mathematics, but how can that be if we never ever apply anything that has to do with the conglomerate {(0,1),(0,0), =>}?

At most we use the proof by contradiction in what comes to the preferred topics for Logicians that originate in Mathematics: If it is and it isn’t, nonsense, and then it can only be that our assumptions are equivocated.

That is the Exclusion Law: It is either (with exclusivity) this or that, never both at the same time.

The Exclusion Law or the Law of the Excluded Middle (LEM) comes attached to the symbol for .and. and that is ꓥ, not =>.

(Horn, 2016)

As a nasty detail, however, there is a strong connection between => and ꓥ in Classical Logic: A material implication is only true, and therefore can only be used for inferences, if the antecedent is false or the consequent is true. That means that only implications that find their conglomerate in the set {(0,0,=>), (0,1,=>), (1,1,=>)} would be good for us to produce inferences.

If we put them together, implication and conjunction, we then have, as a result, that if we get the assertion and its negation as an antecedent or (exclusively) the assertion and its negation as a consequent, we should not be able to use the implication for anything.

Instead, the rule we actually use in Mathematics is that that receives a zero, a verdict of the type false, and therefore it is all actually useful when we produce inferences (we are obviously referring to the proof by contradiction).

Oh, dear: Charming Corcoran now! We have been using other rules all the time in Mathematics, like we have never actually respected Frege and his fellows: In practice, the theory is another, basically.

We simply pass a grotesque liquid paper brush over the Fregean rules as we do Mathematics, and this since the start!

Oh, well, if we actually make that be the system for Mathematics, the one we actually use, we are either going to have a better version of Classical Logic, say what they actually intended, or a new system that is just the formalization of what we already use (so how excruciatingly interesting this all is? - We ask Tom Cruise (The Mummy, version Tom Cruise, marketing token said by Vergara).

Oh, well, this does not look easy. It is like messing up with the untouchable gods of Science, but, to hell, we would not have lost our precious and priceless lives suffering atrocity for nothing, is it not?

We will proceed, Anna Fillipecki (do not cross the line, oppressor and oppressed).

Here we go, for better or worse, whatever may come, please be kind, yet read and criticize.

For completeness, see an extract of a book of ours (Pinheiro, 2016b):

CORCORAN: MATERIAL IMPLICATION x LOGICAL IMPLICATION

Professor Corcoran in The Founding of Logic, Modern Interpretations of Aristotle's Logic (Corcoran, 2016), states that:

To see that not every truth-preserving process is consequence-conservative it is sufficient to consider the rule of mathematical induction which, for example, when applied to the two propositions 'zero is even' and 'every natural number which is the successor of an even natural number is even' results in 'every natural number is even.' This resultant is materially implied by the given premise-set since the second premise is false and, of course, every proposition is materially implied by every set of propositions having a false member. On the other hand, the resultant is not logically implied by the given premise-set. To see this use the method of counterarguments: 'zero is integral' and 'every real number which is the successor of an integral real number is integral' are both true whereas 'every real number is integral' is false, of course; one-half is not integral, for example.

My remarks are as follows:

We all know that (0 and 0) does not give us l in Classical Logic, right? We also know that (1 and 0) does not give us l in CL.See Slide 7 of (Leifer, 2009).

Let's assume, for the sake of the argument, that 0 is an even number, since plenty of people defend that on the Internet. In this case, you have a 1. Even so, the successor of an even is not even, so that the second premise is wrong and you then have to agree that you have a 0 there. As said before, (1 and 0) will give you a zero in CL. Professor Corcoran agrees with all this, for he is saying that it is not logically implied.

zero is even and every natural number which is the successor of an even natural number is even results in every natural number is even.

Here you must notice that this is not a Classical Logic inference because we do not have a few essential premises, such as every natural number is zero or is an even number or is the successor of an even number.

If we were to code that, we would get perhaps A = zero is even, B = every natural number which is the successor of an even natural number is even, C = set of the even numbers, D = every natural number is even, and s(x) = successor of the natural number x. That would result in (0 ∈ C ∧ x ∈ N ∧ (x = s(y), s(y) = y+1, y ∈ C => x ∈ C) ⇒ (x ∈ N ⇒ x ∈ C) or A ∧ B ⇒ D.

Since 0 is an even number, this according to the previous assumptions, v(A) = 1. B is obviously false, so that v(B) = 0. With this, v(A ∧ B) = 0. V(D) = 0 is then as acceptable as v(D)=1, since, when the antecedent is 0 in Classical Logic, all can be implied. If so, we cannot really say that D is true or we cannot really say that D is false, what then matches our information: We do not have enough premises to hang on to. In this case, it is not sound to say that A ∧ B results in D or that

zero is even and every natural number which is the successor of an even natural number is even results in every natural number is even.

Professor John then talks about material implication and the fact that any falsehood, of any premise, would give us anything in exchange, but, we think that would be a reference to something like the Explosion Law and therefore it only happens if we have an implication and a false antecedent, like we see in (Weisstein, 1999).

In this case, when the antecedent is false, the consequent is irrelevant for the result, which is always true. We think that is what Professor Corcoran was referring to here, but it (maybe) ended up containing a bit of inaccuracy.

Here we seem to have a conjunction, and therefore there is no explosion. We always get a zero as a result instead, not one, if we want it to be logically valid. As a result, there is no material inference, only logical: v(A ∧ B ⇒ D) =1 if we assume that v(A) = 1 and v(B) = 1. v(D) must also be 1. Notwithstanding, it is clearly not a material implication because when we put the suggested words there, we do not get soundness.

Having said that, we directed ourselves to (Encyclopaedia, 1998) and found out that some people say that Material Implication is the same as Logical Implication. In this case, the implication mentioned by Doctor Corcoran is actually always materially true.

See:

In most systems of formal logic, a broader relationship called material implication is employed, which is read If A, then B, and is denoted by A ⊃ B or A → B. The truth or falsity of the compound proposition A ⊃ B depends not on any relationship between the meanings of the propositions but only on the truth-values of A and B; A ⊃ B is false when A is true and B is false, and it is true in all other cases. Equivalently, A ⊃ B is often defined as ∼(A·∼B) or as ∼A∨B (in which ∼ means not, · means and, and ∨ means or). This way of interpreting ⊃ leads to the so-called paradoxes of material implication: grass is red ⊃ ice is cold is a true proposition according to this definition of ⊃.

What could then happen is that the implication would not be true in terms of real life, since it is missing elements for us to connect those things as we do, let's say, in a police investigation. We should then invent a new term for that, so say Natural Implication, since Logic is more than logic, which connects to logical systems.

Clarke (1996) states that

A large volume of research shows that humans reason poorly about conditional statements and that the formal notion of material implication is difficult to learn. Textbooks on Logic have used a variety of approaches to the introduction and justification of a truth-functional definition of material implication.

and that

Most commonly, material implication is defined by truth table or some verbal equivalent such as X-->Y is always true if X is false and also if Y is true [HILB50 p4] or A conditional sentence is false if the antecedent is true and the consequent is false; otherwise it is true [SUPP57 p6].

We are then relieved because the term seems to have brought confusion to the writing and understanding of logicians.

(Planetmath.org, 2016) defines Logical Implication and it then looks like both concepts will coincide in the case we here mention: Logical Implication and Material Implication.

We did not feel the necessity of doing the Brazilian and American thing here, just of creating a new term, which is then Natural Implication, to denote what we feel in terms of real life and the Material Implication from Mathematics/Classical Logic.

2. Development

The matter at stake is, first of all, what do we actually use in Mathematics, what logical system?

We obviously only accept (1,1,=>) as a possible entry when the set of possible entries, in Classical Logic, was {(0,0,=>),(0,1,=>), (1,1,=>)} in terms of the material implication instead.

We say that P: a ꓥ~a is false, and therefore we say that v(a ꓥ~a) = 0.

In Classical Logic, P is inadmissible, and therefore there is no P.

We say Contradiction and stop right there, where the conjunction became inconsistent.

Let’s then observe the truth-tables for Classical Logic:

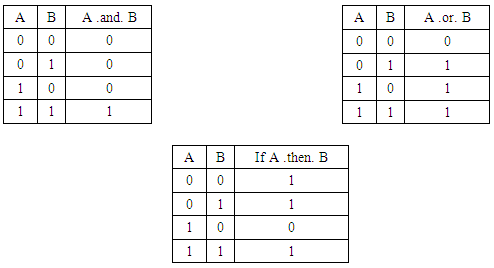Now what we actually use in Mathematics:

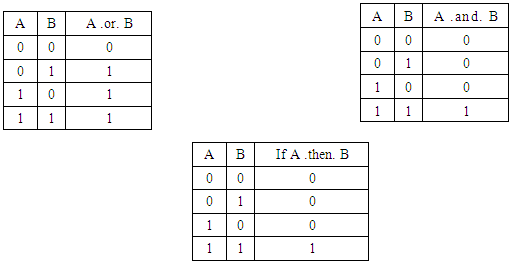Our logical inferences do seem to follow the rules of ordinary thinking, so that if we are both black and beautiful, black and beautiful are things that we can use to make inferences about ourselves. If we are black but not beautiful, we can only use black. If all blacks have dark skin, then it is true that if a person is black they have dark skin.

On the other hand, if we are neither blue nor black, and we say that if we are black then we are blue, this assertion (if we are black then we are blue) can be used to make inferences, so that if we are black and blue then there is no earth is a sound inference.

We can now see the idea of the Ex Falso better, since the falsity has spread, yet this is very confusing, since contradictions should lead nowhere in Mathematics; we discard reasoning whenever we reach a contradiction.

This is not a contradiction. Yet, we do have the sensation that falsity has spread: The antecedent was false, we get a false consequent, and everything is OK.

On the other hand, if the consequent were true in the same situation, everything would also be OK, and that is the thing.

This is true, a true inference in Classical Logic (considering the truth values we had before): If we are black then we are blue.

Yet, we will never use it to prove anything inside of Mathematics.

How can we explain such an amount of incoherence, please?

That is why we’d better change this.

Two lines in a table is not that much mistake.

Could it have been a typo when extracting things from the work of Frege?

It is to wonder.

Not to be believed, that is exactly what we read in Currie (1987): There was a typo when assigning truth-values to the elements of the material implication.

It is either this or we were taught wrong: That Classical Logic was the logical system used in Mathematics.

See (Currie, 1987):

An inference . . . is the passing of a judgment [Urteilsfάllung] made in accordance with logical laws on the basis of previously passed judgments. Each of the premises is a determinate Thought recognized as true; and in the conclusion too, a determinate Thought is recognized as true. [16], pp. 303-304; [10], p. 318

From false premises nothing at all can be concluded. A mere Thought, which is not recognized as true, cannot be a premise. Only after a Thought has been recognized by me as true, can it be a premise for me. Mere hypotheses cannot be used as premises. [18], p. 1823

. . . we can infer something only from true sentences. Thus if a group of sentences contains a sentence whose truth is not yet known, or which is certainly false, then this sentence cannot be used for making inferences. . . .

When we infer we recognize a truth on the basis of other previously recognized truths according to a logical law. [17] in [29], p. 30 and in [25], pp. 16-17

Of course we cannot infer anything from a false Thought. [22] in [16], p. 364 and in [10], p. 375

. . . before recognizing its truth one cannot use a Thought as a premise of an inference, nor can one infer or conclude anything from it. [11] in [16], p.390 and in [10], p. 402

Now the problem becomes this: Would inference be different from implication?

We must go back to the origins of the truth-tables to find out whether there was some mistake in the translation of the words of Frege into those tables.

A relevant extract says that Wittgenstein might have been the murderer. Let’s see (Biletzki, 2014):

Wittgenstein supplies, in the Tractatus, a vivid presentation of Frege’s logic in the form of what has become known as truth-tables. This provides the means to go back and analyze all propositions into their atomic parts, since every statement about complexes can be analyzed into a statement about their constituent parts, and into those propositions which completely describe the complexes (TLP 2.0201). He delves even deeper by then providing the general form of a truth-function (6). This form, [p¯,ξ¯,N(ξ¯)][p¯,ξ¯,N(ξ¯)], makes use of one formal operation (N(ξ¯))(N(ξ¯)) and one propositional variable (p¯)(p¯) to represent Wittgenstein’s claim that any proposition is the result of successive applications of logical operations to elementary propositions.

And a relevant extract from Tractatus is: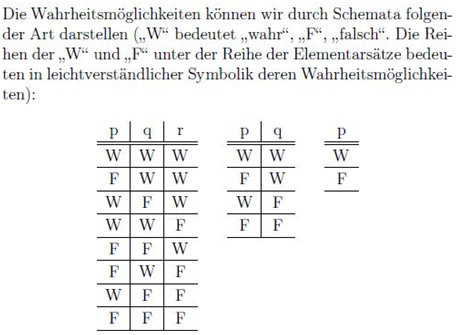

(Wittgenstein, p. 120, 2010)

It is perhaps clear enough that F is for false. W therefore is for true.

It appears to us that he is just trying to get us used to how things work in his logical system, so that there is no actual relationship for us to make sense of. This seems to be a slow teaching method, which starts with us getting familiarized with the way things work.

R there could stand for result. He is then referring to the parts of the assertion, those before and after the connector, so say =>. It is just for us to get used to the idea of truth-values being assigned to those parts and a result being attained: A true or a false.

(Wittgenstein, p. 56, 2010)

That seems to have a lot in common with what some of the opponents of the Classical Logic system have been claiming throughout time: There should be some connection in terms of sense between antecedent and consequent in an implication.

(Wittgenstein, p. 56, 2010)

5.1241 seems to clearly agree with what we saw previously in this paper: (1, 1, =>) is definitely seen as a true assertion in the Classical Logic system.

(Wittgenstein, p. 58, 2010)

(Wittgenstein, p. 59, 2010)

(Wittgenstein, p. 57, 2010)

(Wittgenstein, p. 36, 2010)

Since this is all we found that could be relevant in the Tractatus, it is clearly the case that nothing like the Ex Falso was ever mentioned, and it is still precisely the opposite, it seems: It all seems to consistently point at what we currently use in our mathematical proofs, that is, (1,1,=>) is the only acceptable way to go in an inferential move.

(Birjukov, 2012) brings very interesting pieces of information:

go, if-then is only supposed to be used with formal implications, like we should only translate => into if-then in that situation. The material implication is a situation in which we could never ever use if-then.

That that would be the correct understanding of Frege’s work… .

(Edgington, 2014)

Here we then reinforce the view that the material implication is the one with the table we currently attribute to Classical Logic.

(Weber, 2016)

(Weber, 2016)

Here we see mention to the Ex Falso, but the interesting thing is that it is not coming from those who wrote Classical Logic if we consider what we know from studying the texts here: It is coming exclusively from the people who wrote the source, that is, from Weber.

Here we have the truth tables we usually call Classical Logic being mentioned once more.

(Wittgenstein, p. 53, 2010)

Here we can see that Wittgenstein says that from contradiction we infer nothing. We still see that contradictions should be false, so that we here have what we have called, in this paper, the Mathematical Logic instead.

Yet another source states:

E. Wittgenstein’s philosophy of logic: Some very basic commitments of the Tractatus:

1. Every proposition has a modal status, i.e., is either a tautology (thus necessary), a contradiction (thus impossible), or has sense (thus contingent) (4.464, 5.525).

(Boedeker, 2017)

In this way, it seems that our proposed fixing is more than adequate.

It is missing studying soundness and completeness, Priest’s style (Priest, 2001), in what regards our new Classical Logic or our Classical Logic’.

Let’s then, for this purpose, study the proposed truth tables once more: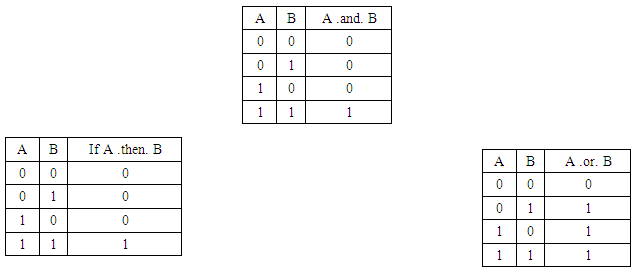

The only table that changed was the implication table, so that we must worry only about that one.

Given A => B false, that would be because B is false (if B is false, the implication is always false) or A is false (whenever A is false, the implication is false).

Given A => B true, we have that B is true and A is true or that not (B false or A false).

If A is false, the implication is false. If B is false, the implication is false. If neither A is false nor B is false, the implication is true.

OK.

In Classical Logic, we say that either the antecedent is false or the consequent is true for us to have a true implication. That won’t be true anymore.

That won’t change any theorem we currently have, however: All we use is (1,1,=>), as said before, this in all mathematical proofs.

The Ex Falso is told to be an issue with Classical Logic. If we replace Classical Logic with Classical Logic’, we won’t have this issue anymore.

3. Conclusions

It seems that the so called formal implication, which is the implication we use in Classical Logic, was not seen as a place where the symbol => or Ɔ could be translated into an if-then, so that it is a mistake doing that. Frege, in more recent writings, started doing that, however.

Material implication should mean can be applied to Purely Human Language (Pinheiro, 2013), and formal implication should mean not necessarily.

In this case, the counter-examples here presented, including those presented by Doctor Corcoran, would not be that relevant in what comes to proving that Classical Logic has something that should be changed.

In compensation, we have investigated the issue deeper and found out that the logical system we currently apply in Mathematics (the one we have always applied) is not really what we currently call Classical Logic: We actually apply a system that is very similar but differs when it comes to the implications.

We could perhaps call this new system, with truth-tables exhibited in this paper, Mathematical Logic, but we could also fix Classical Logic in order to make it match our intuition (so that we would not have the counter-examples we here present anymore) and the human discourse (so that material and formal implication would equate).

Since Classical Logic comes from the sigmatoid classicists, classical period in Logic, that would connect to Frege, Russell, and Peano. In this case, we must also consider Wittgenstein. All seems to form a coherent body of information that leads us to believe that the only possible intention was the Mathematical Logic.

In this case, Classical Logic is the Mathematical Logic and what we have is a generalized mistake in the interpretation of what the creators of Classical Logic said.

If we replace Classical Logic with Classical Logic’, no major problems will occur. With all that we have in Mathematics so far, in terms of results, nothing changes.

Ex Falso will stop being an issue, however.

We will also have to change the so famous sentence, if the antecedent is false or the consequent true, we have a true implication. We will now say that if the antecedent or the consequent is false, we have a false implication.

Nothing changes in terms of The Sorites, The Liar, The Hanging or Zeno’s Paradox, since, as one can see in (Pinheiro, 2016c), (Pinheiro, 2016d), (Pinheiro, 2016e) and (Pinheiro, 2012), the solution to these paradoxes doesn’t have a lot to do with Classical Logic.

Contradictions would now be evaluated as false, what does not allow us to infer anything from them. We have always used this in our mathematical proofs: We get a contradiction and we then say that our assumption is false.

Note

1. Colegio da Compania Santa Teresa de Jesus (College of the Company Saint Therese of Jesus)