1. Introduction

Critical node detection problems (CNDP) are a family of optimization problems defined on graphs, where one is required to select a small set of nodes to remove in order to make the remaining graph as disconnected as possible, according to some connectivity measure. In particular, the connectivity measure analyzed in this paper is the so-called pairwise connectivity, formalized in [5], which counts the number of node pairs that are connected to each other by a path. This class of problems has attracted the interest of many researchers in the last two decades, because of its relevance in a number of practical applications. The applications involve scenarios in which the goal is to either secure the most critical nodes in a network or attack the most critical nodes in order to have the fewest connections between any two nodes in the network. Below are some of the most important applications of critical node detection problems.

The connections between pairs of nodes are minimized after the most critical nodes are removed from a supply chain network. A military supply chain network [33], for example, consists of battalions and support battalions as nodes and the connections between them as links. By attacking the most critical nodes in this network, the connectivity between supply and demand nodes will be reduced. As a result, solving the critical node detection problem (CNDP) is critical in military tactical attacks during wars.

Terrorists can be represented as nodes in a graph using information obtained from a covert network, with social interactions between them as links. We can reduce terrorist communication by targeting the most critical individuals in the networks [18].

In order to analyze the influence of epidemics in genuine social networks [22], people and their connections are represented as nodes and links in a graph. Since random mass vaccines are expensive [22], numerous solutions for targeted vaccinations were offered to reduce the spread of infectious illnesses in genuine social networks. However, the best vaccine technique is to identify and vaccinate important nodes in order to reduce pairwise connectivity between persons in a community [5], assuming that higher pairwise connectivity causes faster outbreaks.

Telecommunication networks, such as the Internet, telephone networks, and computer networks, can be visualized as graphs, with each node representing a terminal and links representing communication between terminals. In telecommunication networks, we aim to stop a virus from spreading or discover a strategy to decrease network [6] communication as much as feasible. Also, with network vaccination [19], where a graph reflecting individuals's contacts is provided, only a certain number of people can be vaccinated, and we intend to keep the virus [10,34] from spreading.

The CNDP's applications are not restricted to those listed above; it has a wide range of uses in a variety of fields, including transportation engineering [17], computational biology [24,32], the analysis of complex networks [8,14], security/vulnerability issues in networks [13,23,30,31], homeland security [9,15,16], energy [27], etc.

Since problems of this type usually turn out to be NP-hard for general graphs, and often also for quite special classes of graphs [2,11,28,29,30], several heuristic approaches as well as methods based on integer programming formulations have been proposed in the literature; see, e.g., [1,3,5,12,23,25,26]. Polynomial algorithms are instead available only for some particular cases, which are usually limited to graphs with bounded treewidth, in particular trees and series-parallel graphs [2,4,7,11,20,28]. We refer the interested reader to the survey [21] for a detailed overview.

2. The Problems that We Study

In this paper we study the Critical Node Detection Problem on a path which can be seen as a very special case of a tree. Given a path grap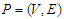h with 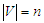nodes and an integer 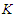, the CNDP on a path seeks to find a set 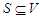of at most 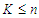nodes, the deletion of which minimizes pairwise connectivity in the remaining path graph 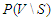. We will tackle the so-called Distance-based Critical Node Detection Problem (D-CNDP) over paths as described in [4]. The NP-completeness of D-CNDP over paths for some specific distance functions has been already established [4]. We look at some particular versions of CNDP on paths that fall into the D-CNDP on paths and provide closed-form solution for optimality of the objective function. The variants that we analyze in this paper are the following:

1. Minimizing the number of node-pairs connected by a path with upper bound of length at most .

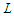2. Minimizing the number of node-pairs connected by a path with lower bound of length at least .

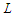3. Minimizing the number of node-pairs connected by a path of length precisely .

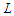4. Minimizing the number of node-pairs connected by a path of length between 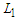and 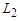where 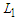and 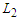are the lower and upper bound respectively.

The term balanced solution is an important concept that we will utilize in the following statements. We call the solution balanced if the difference between the length of the shortest and longest components is either 0 or 1.

Before deriving the exact solution of the objective function for the four variants introduced above, we first present the following result without any lower or upper bound on the length of the connecting path.

Proposition 1. For the CNDP on a path without any lower or upper bound, the optimal solutions are the balanced solutions.

Proof. Let 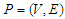be a path graph with 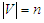nodes and let 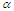be the average number of nodes of the sub-paths obtain after removing 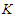nodes, where .

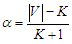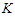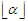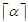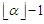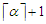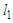Assume that we are given an optimal solution after removing nodes. Suppose by contradiction that in the given optimal solution, not all the sub-paths have length or . Since the solution is unbalanced, there are at least two sub-paths in this solution in which one of the component has length at most and another component has length at least . Let and 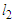be the number of nodes of the shortest and the longest components respectively, i.e., 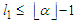and 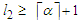(see Figure 1). Now we construct a new solution by adding one node in the shortest component, i.e., 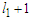and by subtracting one node in the longest component, i.e., 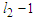and the length of the other components are unchanged (see Figure 2). We want to show that this new solution is better than the given solution.

So the claim is

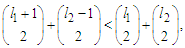where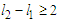

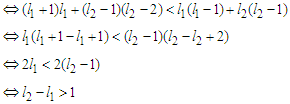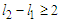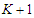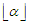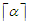which is true by assumption because we are assuming , and we will continue this perturbation until we have components of size and , and this shows that every optimal solution is balanced. Observe that all balanced solutions have the same cost and hence they are equivalent. Since all balanced solutions are equivalent, this proves that all balanced solutions are optimal.

We now state the result when the graph is a path and the problem is to remove 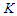nodes in order to minimize the number of pairs that are connected by a path of length at most 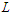, for some given natural number .

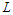Proposition 2. For the CNDP on a path with upper bound 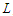, any solution that removes 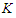nodes and creates 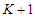components with cardinality at least 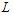is optimal. If no such a solution exists, then any solution that removes 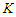nodes and creates balanced components is optimal.

Figure 1. Example of a solution after removing K = 2 nodes

Figure 2. Modification of the solution of Figure 1

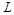Proof. First we prove the second part of the statement which means there is no way to make all the components with cardinality at least and in this case we want to prove that balanced solutions are optimal.

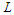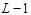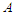Assume by contradiction that we are given an optimal solution which is not balanced. Since we are assuming that there is no way to make all the components with cardinality at least , there is at least one sub-path with cardinality at most . Let be the shortest component and 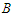be the longest component of the solution. With a slight abuse of notation we will denote by 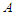and 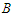also the number of nodes in the component. Then 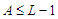and 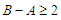because the solution is not balanced. Now we do the perturbation by adding one node in the shortest component and by subtracting one node in the longest component and by keeping the cardinality of all other components unchanged. Now if 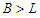and we subtract a node from 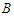, then we lose 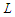connections, while if 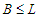and we subtract a node from 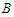, then we lose 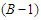connections because we have to count only the paths of length 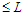. Since 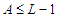, if we add an extra node to 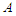, then we have 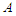new connections. Thus we have the following two cases when we do the perturbation.

Case 1: If 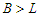, then the improvement is .

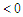Case 2: If 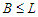, then the improvement is 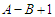which becomes 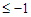because we are assuming that

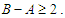So with the property 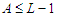, we have always a negative improvement (case 1 and 2), i.e., we reduce the objective function and this proves that any unbalanced solution is not optimal. Since all balanced solutions are equivalent, this proves that all balanced solutions are optimal.

Now we prove the first part of the statement which means that it is possible to make all the sub-paths with cardinality at least 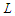. In this case still it is possible that in the solution the shortest component is smaller than 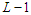and we know by the above argument that this solution is not optimal.

In the following we prove that all the solutions that creates 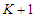sub-paths with cardinality at least 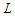are equivalent.

When we remove 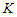nodes from the path, we create 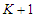components. Suppose 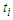is the number of edges of every sub-path. Now if we take a path with 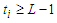edges, then the contribution is given by 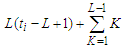, because in a component of 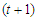nodes, we have 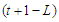nodes which gives a contribution of length 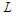and the remaining 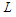nodes gives the contribution of 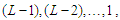respectively, which is given by 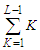. In the last component, the number of edges is given by 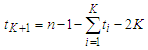, because we have 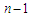edges initially, then we have to discard all the edges of the sub-paths which is given by 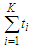and when we are removing 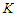nodes, we are deleting 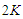edges, since we are assuming that we are creating 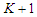components that means we are not removing two adjacent nodes. So the contribution of the 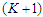th component is given by 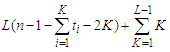. Hence the total contribution is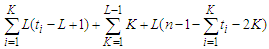

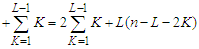which is independent of 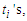that means it does not matter what is the length of the sub-paths as long as their cardinality is at least

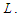Now we show that all the solutions that create all components with cardinality at least 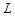are optimal. Define 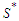as the set of solutions which have the property that all components have at least 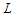nodes. Since there is at least one solution with all the components with cardinality at least 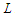, the set 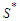is nonempty. Take a solution in 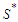. This solution has the property that the total number of nodes in the surviving components is at least 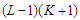as after removing 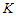nodes we have 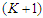components and each of cardinality at least 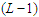. 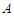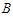Let's call again and be the shortest component and the longest component respectively in 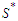. Take any solution which is not in 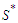, which means that it has at least one component whose cardinality must be smaller than 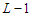, so that 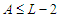. We claim that the cardinality of the longest component is at least 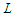, i.e., 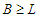. If this is not true, then 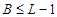. In this case the total number of nodes in the surviving components is at most 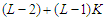, which is at least one unit smaller than 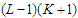and this is a contradiction because we know that the total number of nodes can not be changed as we always remove 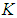nodes. So any solution which is not in 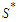has the property that 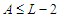and 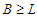and this means that the solution is not balanced. Since the solution is not balanced, we apply the perturbation and by the previous arguments (case 1 and case 2) we know that when we do the perturbation we always improve. After the perturbation either we find a solution which is in 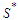and we are done, or we find a solution which has still the property that 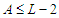and 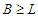and we will continue this perturbation until the solution is balanced. When we get a balanced solution, we are in 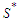and this proves that the set 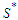is optimal.

The following result holds for the case when the graph is a path and the problem calls for minimizing the number of node-pairs still connected by a path of length at least 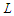, for some given natural number 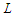, surviving in a path after having removed at most 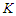nodes..

Proposition 3. For the CNDP on a path with lower bound 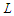, any solution that removes 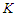nodes and creates 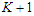components with cardinality at most 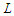is optimal. If no such a solution exists, then any solution that removes 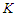nodes and creates balanced components is optimal.

Proof. First consider that we can make all the components with cardinality at most 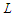and in this case all the solutions are equivalent and hence optimal, because the objective value is 0 and in this incident, it does not matter whether the solution is balanced or not as long as all the components have cardinality at most .

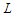Now we prove the second part of the statement which means there is no way to make all the components with cardinality at most 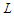and in this case we want to prove that balanced solutions are optimal.

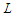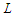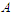Assume by contradiction that we are given an optimal solution which is not balanced. Since we are assuming that there is no way to make all the components with cardinality at most , there is at least one sub-path with cardinality greater than . Let be the shortest component and 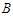be the longest component of the solution. With a slight abuse of notation we will denote by 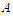and 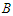also the number of nodes in the component. Then 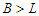and 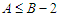because the solution is not balanced. Now we do the perturbation by adding one node in the shortest component and by subtracting one node in the longest component and by keeping the cardinality of all other components unchanged. Now if 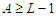and we add an extra node to 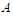, then we have 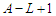new connections while if 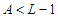and we add an extra node to 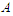, in this case we create 0 connection, because we have to count only the paths of length 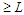. Since 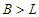and we subtract a node from 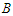, we lose 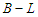connections. Thus we have two cases when we do the perturbation.

Case 1: If 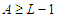, then the improvement is 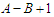which becomes 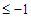because we are assuming that .

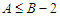Case 2: If 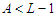, then the improvement is 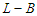which becomes 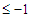because .

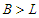So when we have at least one sub-path with cardinality at least 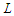, we always get a better solution and this proves that any unbalanced solution is not optimal. Since all balanced solutions are equivalent, this proves that all balanced solutions are optimal.

When the graph is a path, and we want to minimize the number of node-pairs still connected by a path of precise length 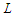, for some given natural number 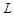, surviving in a path after having removed at most 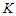nodes, the following result holds.

Proposition 4. For the CNDP on a path of precise length 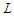, any solution that removes 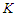nodes and creates 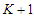components with cardinality at least 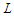is optimal. Otherwise, any solution that creates 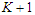components with cardinality at most 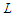is optimal. If no such a solution exists, then any solution that removes 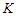nodes and creates balanced components is optimal.

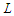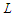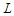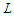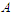Proof. Assume by contradiction that we are given an optimal solution which is not balanced. We are assuming that there is no way to make all the components with cardinality at least or all the components with cardinality at most . Then there is at least one sub-path with cardinality less than and at least one sub-path with cardinality greater than . Let be the shortest component and 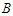be the longest component of the solution. With a slight abuse of notation we will denote by 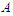and 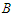also the number of nodes in the component. Then 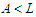, 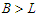and 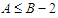because the solution is not balanced. Now we do the perturbation by adding one node in the shortest component and by subtracting one node in the longest component and by keeping the cardinality of all other components unchanged. Since 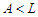, when we add an extra node to 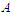, we create 0 connection, because we have to count only the paths of length precisely 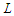. Again since 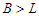, when we subtract a node from 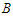, we lose 1 connection. Thus we have the following case when we do the perturbation.

Case 1: If 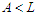and 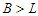, then the improvement is .

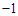In the following we prove that all the solutions that creates 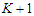sub-paths with cardinality at least 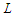are equivalent.

When we remove 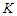nodes from the path, we create 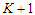components. Suppose 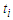is the number of edges of every sub-path. Now if we take a path with 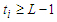edges, then the contribution is given by 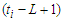, because in a component of 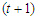nodes, we have 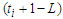nodes which gives a contribution of length exactly 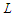. In the last component, the number of edges is given by 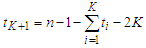, because we have 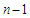edges initially, then we have to discard all the edges of the sub-paths which is given by 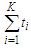and when we are removing 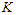nodes, we are deleting 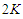edges, since we are assuming that we are creating 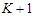components that means we are not removing two adjacent nodes. So the contribution of the 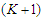th component is given by 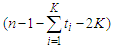. Hence the total contribution is

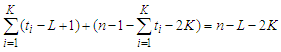which is independent of 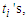that means it does not matter what is the length of the sub-paths as long as their cardinality is at least 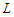and this proves that all the solutions that creates long components are all equivalent.

Now we show that all the solutions that create all components with cardinality at least 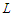are optimal. Define 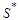as the set of solutions which have the property that all components have at least 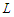nodes. Since there is at least one solution with all the components with cardinality at least 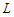, the set 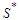is nonempty. Take a solution in 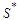. This solution has the property that the total number of nodes in the surviving components is at least 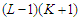as after removing 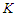nodes we have 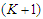components and each of cardinality at least 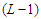. 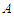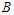Let's call again and be the shortest component and the longest component respectively in 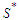. Take any solution which is not in 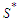, which means that it has at least one component whose cardinality must be smaller than 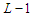, so that 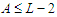. We claim that the cardinality of the longest component is at least 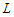, i.e., 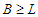. If this is not true, then 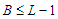. In this case the total number of nodes in the surviving components is at most 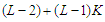, which is at least one unit smaller than 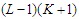and this is a contradiction because we know that the total number of nodes can not be changed as we always remove 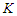nodes. So any solution which is not in 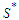has the property that 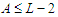and 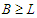and this means that the solution is not balanced. Since the solution is not balanced, we apply the perturbation and by the previous arguments (case 1) we know that when we do the perturbation we always improve. After the perturbation either we find a solution which is in 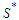and we are done, or we find a solution which has still the property that 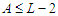and 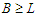and we will continue this perturbation until the solution is balanced. When we get a balanced solution, we are in 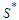and this proves that the set 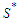is optimal.

Similarly, if we can make component in such a way that the cardinality of all components is shorter than 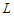, then all the solutions are equivalent and hence optimal, because the objective value is 0 and in this incident, it does not matter whether the solution is balanced or not as long as all the components have cardinality at most .

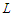Otherwise, if we can not make solution in which all the components have cardinality at least 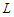or at most 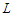, then obviously we are in case 1, because case 2 is not possible and in this case we always have a negative improvement, i.e., we reduce the objective function and this proves that any unbalanced solution is not optimal. Since all balanced solutions are equivalent, this proves that all balanced solutions are optimal.

In the following we state the result when the graph is a path and the problem is to remove 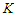nodes in order to minimize the number of pairs that are connected by a path of length at least 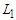and at most .

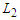Now we consider the case in which we have a lower bound 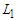and an upper bound 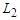and we consider the connections which are between 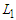and .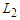

Proposition 5. For the CNDP on a path with lower bound 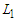and upper bound 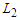, any solution that removes 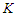nodes and creates 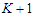components with cardinality at least 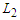is optimal. Otherwise, any solution that creates 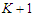components with cardinality at most 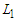is optimal. If no such a solution exists, then any solution that removes 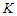nodes and creates balanced components is optimal.

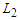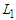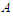Proof. Assume by contradiction that we are given an optimal solution which is not balanced. We are assuming that there is no way to make all the components with cardinality at least or all the components with cardinality at most . Let be the shortest component and 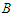be the longest component of the solution. With a slight abuse of notation we will denote by 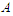and 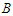also the number of nodes in the component. Then 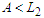, 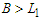and 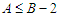because the solution is not balanced. Now we do the perturbation by adding one node in the shortest component and by subtracting one node in the longest component and by keeping the cardinality of all other components unchanged. Since we want to count the paths of length between 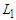and , if 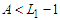and we add an extra node to , then we have new connection while if 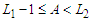and we add an extra node to 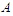, in this case we create 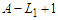connections. Again if 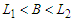and we subtract a node from 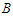, then we lose 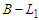connections while if 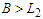and we subtract a node from 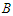, then we lose 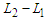connections. Thus we have the following cases when we do the perturbation.

Case 1: If 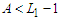and 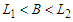, then the improvement is 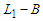which becomes 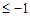because .

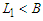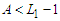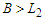Case 2: If and , then the improvement is 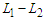which becomes 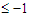since .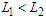

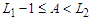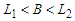Case 3: If and , then the improvement is 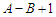which becomes 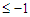because we are assuming that .

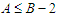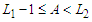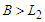Case 4: If and , then the improvement is 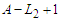which becomes 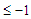because .

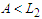If we can make all the components with cardinality at most 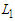, then all the solutions are equivalent and hence optimal, because the objective value is 0.

In the following first we prove that all the solutions that creates 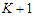sub-paths with cardinality at least 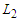are equivalent.

When we remove 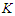nodes from the path, we create 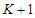components. Suppose 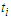is the number of edges of every sub-path. Now if we take a path with 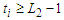edges, then the contribution is given by 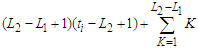, because in a component of 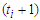nodes, we have 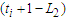nodes which gives a contribution of 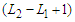and the remaining 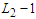nodes gives the contribution of 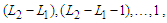respectively, which is given by 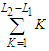. In the last component, the number of edges is given by 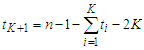, because we have 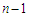edges initially, then we have to discard all the edges of the sub-paths which is given by 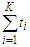and when we are removing 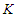nodes, we are deleting 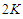edges, since we are assuming that we are creating 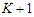components that means we are not removing two adjacent nodes. So the contribution of the 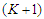th component is given by 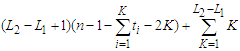. Hence the total contribution is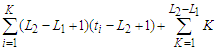

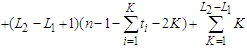
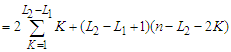which is independent of 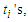that means it does not matter what is the length of the sub-paths as long as their cardinality is at least 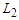and this proves that all the solutions that creates long components are all equivalent.

Now we show that all the solutions that create all components with cardinality at least 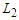are optimal. Define 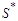is the set of solutions which has the property that all components have at least 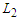nodes. Since there is at least one solution with all the components with cardinality at least 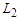, the set 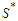is nonempty. Take a solution in 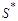. This solution has the property that the total number of nodes in the surviving components is at least 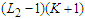as after removing 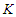nodes we have 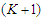components and each of cardinality at least 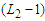. 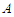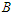Let's call again and be the shortest component and the longest component respectively in 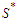. Take any solution which is not in 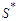, which means that it has at least one component whose cardinality must be smaller than 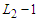, so that 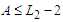. We claim that the cardinality of the longest component is at least 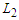, i.e., 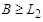. If this is not true, then 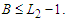In this case the total number of nodes in the surviving components is at most 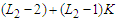, which is at least one unit smaller than 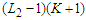and this is a contradiction because we know that the total number of nodes can not be changed as we always remove 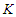nodes. So any solution which is not in 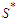has the property that 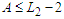and 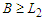and this means that the solution is not balanced. Since the solution is not balanced, we apply the perturbation and by the previous arguments (case 2 and case 4) we know that when we do the perturbation we always improve. After the perturbation either we find a solution which is in 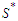and we are done, or we find a solution which has still the property that 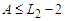and 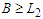and we will continue this perturbation until the solution is balanced. When we get a balanced solution, we are in 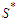and this proves that the set 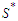is optimal.

Otherwise, if we can not make solution in which all the components have cardinality at least 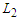or at most 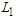, then we are in one of the four cases and in every case we always have a negative improvement, i.e., we reduce the objective function and this proves that any unbalanced solution is not optimal. Since all balanced solutions are equivalent, this proves that all balanced solutions are optimal.

3. Conclusions

In this paper we focused our study on identifying critical nodes from a graph, whose deletion results in the minimum pairwise connectivity among the remaining nodes. We studied a particular case of the critical node detection problem, namely the Distance-based Critical Node Detection Problem (D-CNDP) over paths. We considered four versions of the D-CNDP on paths and provided closed-form solution to solve the problems.