1. Introduction

Transportation is important for human being activity as the economy grows. Under rapid growing economy, it always happens negative impact by growing transportation because of transportation demand versus infrastructure development such as road construction, traffic control management system, public transportation implementation, and so on. Negative impact occurs as traffic congestion, traffic accident, unnecessity fuel consumption, environment destruction, air pollution, noise pollution, traffic fatality as transportation issues in general. There is no exception but this transportation issue in the world, not only developing countries but also advanced countries. Therefore it is important to understand traffic flow condition and mechanism of traffic congestion reason at least. After collecting traffic data and analysis, it digs into traffic flow problem and shows important traffic flow parameter for traffic congestion with using actual traffic measurement data in major cities. Traffic models can be used for several applications, and much attention has been given to research on traffic models. The traffic flow model first developed by Lighthill and Whitham (1955) and Richard (1956)] shortly is known as LWR model [1-3]. In [5-9] describe finite difference scheme for a fluid dynamic traffic flow model.

The basic features of the LWR model prescribe in Klar [2], Habermann (1977) [4]. Additions are made after the development of these traffic models and other models have been developed. There are different types of traffic flow models and they can be classified in various ways. A good number of numerical solutions for macroscopic multilane traffic flow models are found in literature [10-15]. Thus, the main objective of this paper three lane traffic model approximated a linear velocity-density relationship which is system of first order hyperbolic partial differential equation with unknown variable density. It is impossible to find the exact solution of the multilane traffic model. So, there is a demand to find the numerical solution of considered traffic model and present the descretization which leads to the first order explicit upwind difference scheme (EUDS) and also second order Lax-Wendroff difference scheme (LWDS). The numerical simulation of 10 km highway of three lane is performed for 6 minutes using both the numerical schemes based on artificially generated initial and boundary data. Finally, we verify some experimental results for both schemes. The stability conditions of EUDS and LWDS for considered model are 0.0668 and 0.5171 respectively. Three lane mathematical model of traffic flow in section 2. In section 3-4, numerical solution of first and second order and section 5 performing computed numerical experiments and finally we conclusions.

2. Mathematical Equation of Three Lane Traffic Flow Model

Consider multilane traffic flow model for three lanes

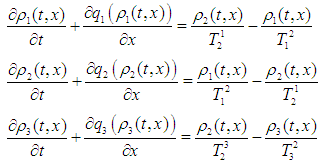(1)

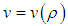Here, velocity as a function of density and flux 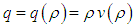and Greenschield’s linear density-velocity relation is 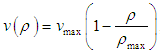where 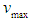is maximum velocity and 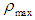is maximum density. Therefore, the flux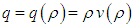

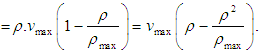
3. First Order EUDS for Three Lane Traffic Flow Model

The first order system of non-linear partial differential equation for three lane traffic flow model as follows:

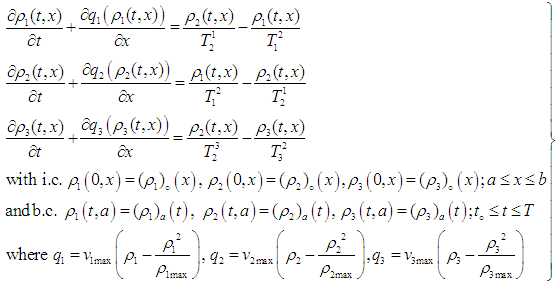(2)

We discretize the time derivatives by the first order forward difference in time and the space derivatives by first order backward difference in space. Therefore, the explicit upwind difference scheme [15] of the non-linear first order PDE (2) takes the form

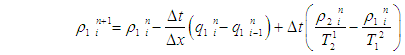(3)

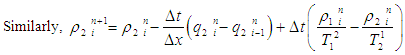(4)

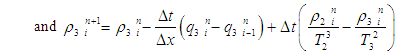(5)

Where

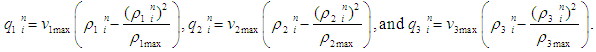So, equations (3), (4) and (5) are the explicit upwind difference scheme for the IBVP (2).

The well-posed-ness and stability condition of EUDS [8] is guaranteed by the simultaneous conditions 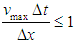and 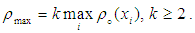In case of three lane traffic flow model are also remain unchanged for our considered model of above condition.

4. Second Order LWDS for Three Lane Traffic Flow Model

The numerical solution of second order Lax-Wendroff difference scheme as an IBVP with two sided boundary conditions reads as follows:

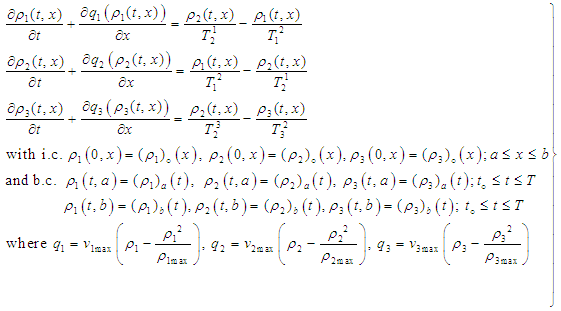(6)

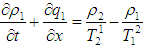In this method, we discretize the time derivatives by the first order forward difference in time and the space derivatives by second order centred difference in space and also in Taylor’s series expansion the time derivatives can be replaced space derivatives in , by Cauchy-Kawalewski technique. Then the Lax-Wendroff difference scheme [14] of the first order non-linear PDE (6) takes the form

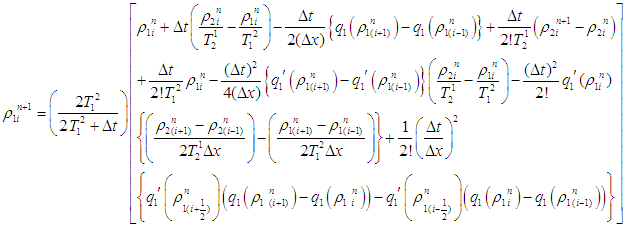(7)

Similarly,

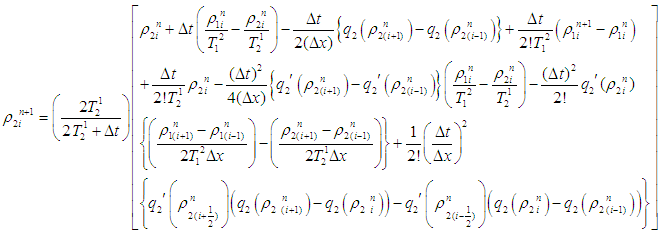(8)

and

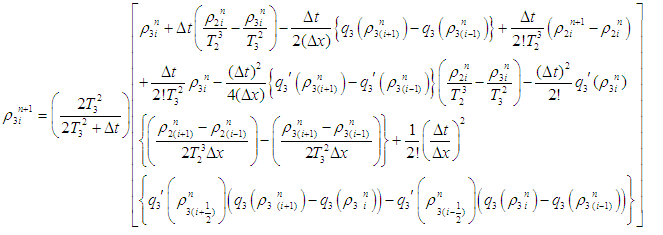(9)

where

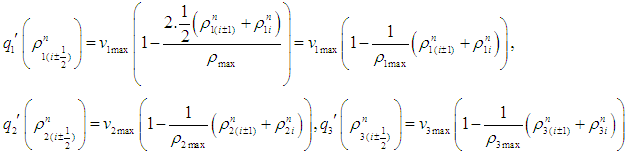and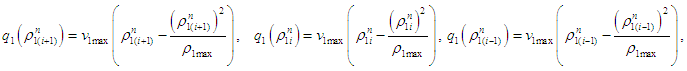

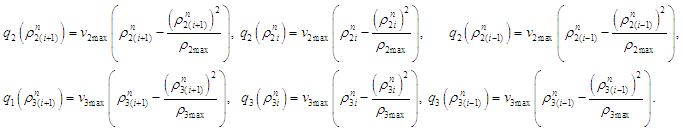Equations (7), (8) and (9) are the Lax-Wendroff schemes for the IBVP (6).

The well-posed-ness and physical constraint conditions of Lax-Wendroff difference difference scheme [9] is guaranteed by the simultaneous conditions 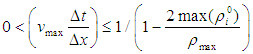and 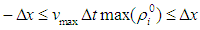and also remain unchanged for our considered three lane traffic flow model.

5. Numerical Results and Discussion

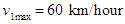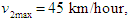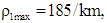
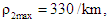
In this section, we implement the numerical schemes of first order EUDS and second order LWDS and also present the outcome of traffic flow simulation for a variety of traffic flow parameters. Here, we choose maximum velocity, and of three lanes respectively. For satisfying the CFL condition we pick the unit of velocity as km/sec and choose maximum density 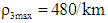and perform the numerical experiment for 6 minutes. We consider the different initial density of multilane traffic flow model for three lanes are 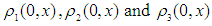. The transition rate from the second lane to the first lane 20%, the first lane to the second lane 10%, the second lane to the third lane 20% and the third lane to the second lane 10%. We implement of above artificial initial and boundary data of three lane traffic flow model of EUDS and LWDS. Also we verify the well-known qualitative behaviors of different traffic flow variables of multilane traffic flow model for three lanes. We run the program and attain the initial density profiles as shown in figure 1.

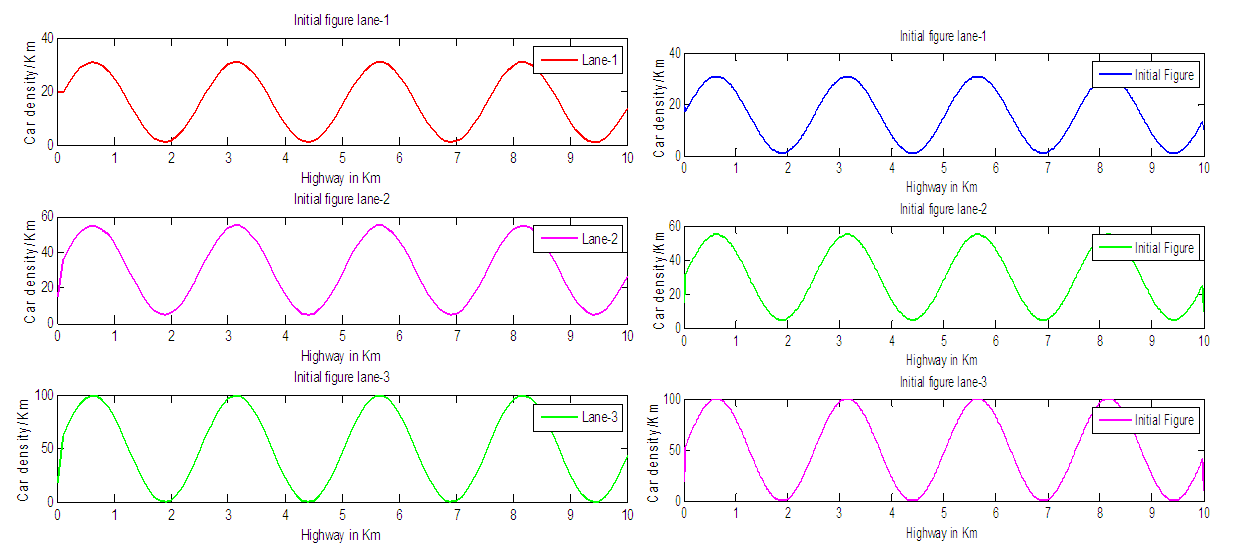Figure 1. Initial density profile of EUDS and LWDS

We run the behavior of car density with respect to highway in 10 km with the different initial density, maximum density and maximum velocity of three lanes respectively for 6 minutes. The computed density profile as shown in figure 2 and desired traffic waves are moving much slower than that in lane-1. Also we observed that as time goes on the traffic wave is moving forward with reducing wave height and the traffic waves in lane-1 are also faster than lane-2 & lane-3.

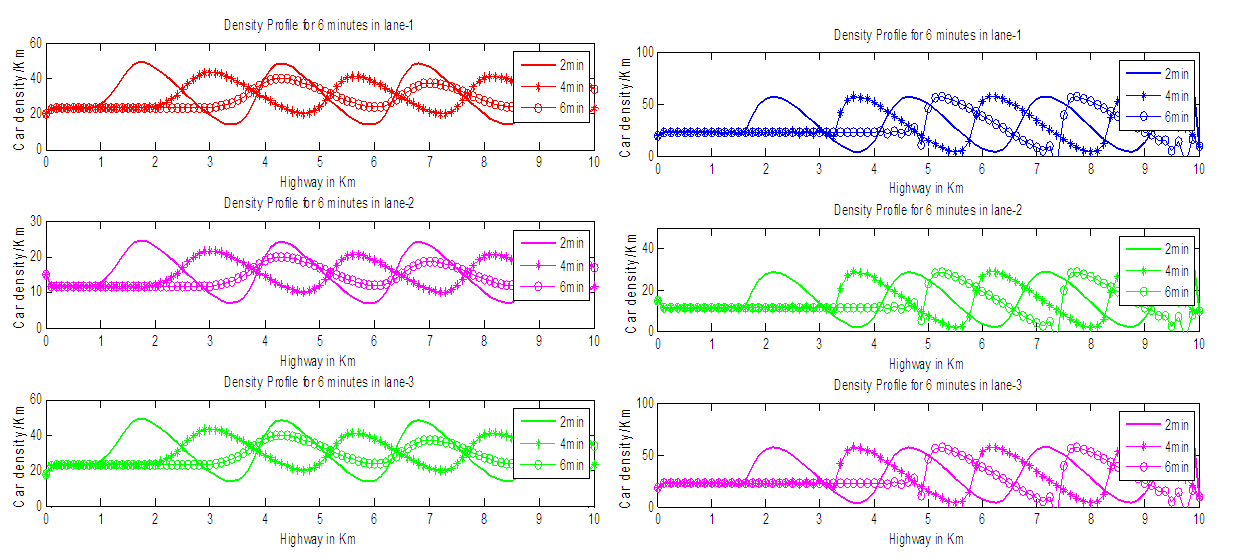Figure 2. Density profile of EUDS and LWDS

The corresponding velocity profile of three lanes with respect to the distance. We run the behavior of car velocity with respect to highway in km for 6 minutes. Here we observe that, as time goes on, the traffic wave is moving forward.

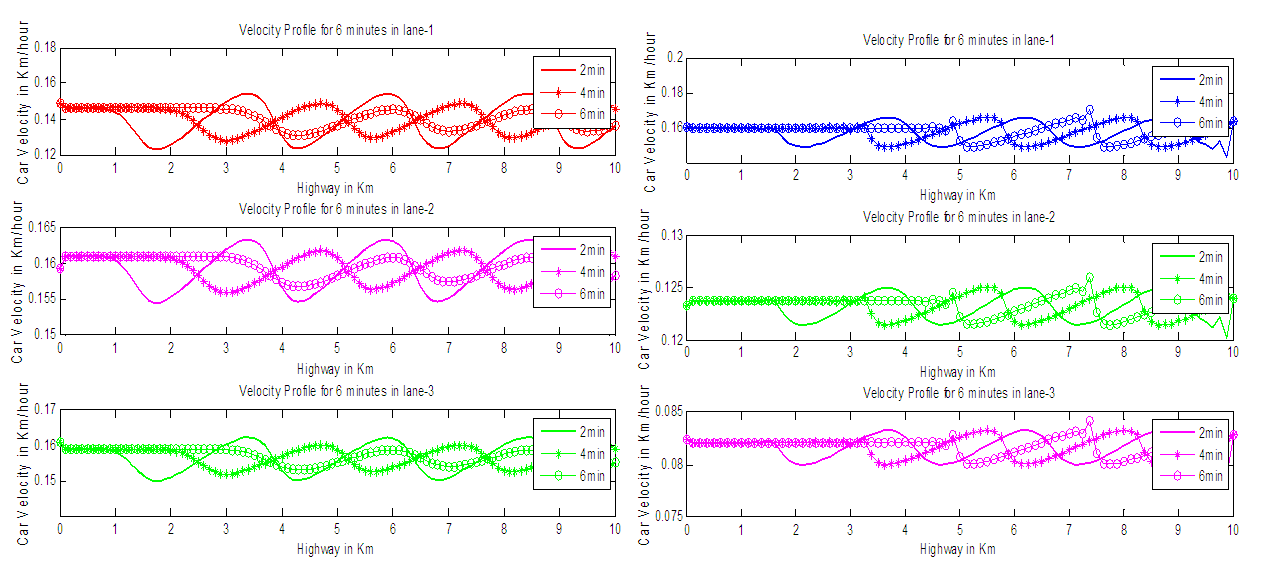Figure 3. Computed velocity profile using EUDS and LWDS

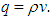We calculate the flux profile of three lanes using flux-density formula Figure 4 represents the computed flux with respect to the distance for 6 minutes. Here we observe that, as time goes on, the traffic wave is moving forward.

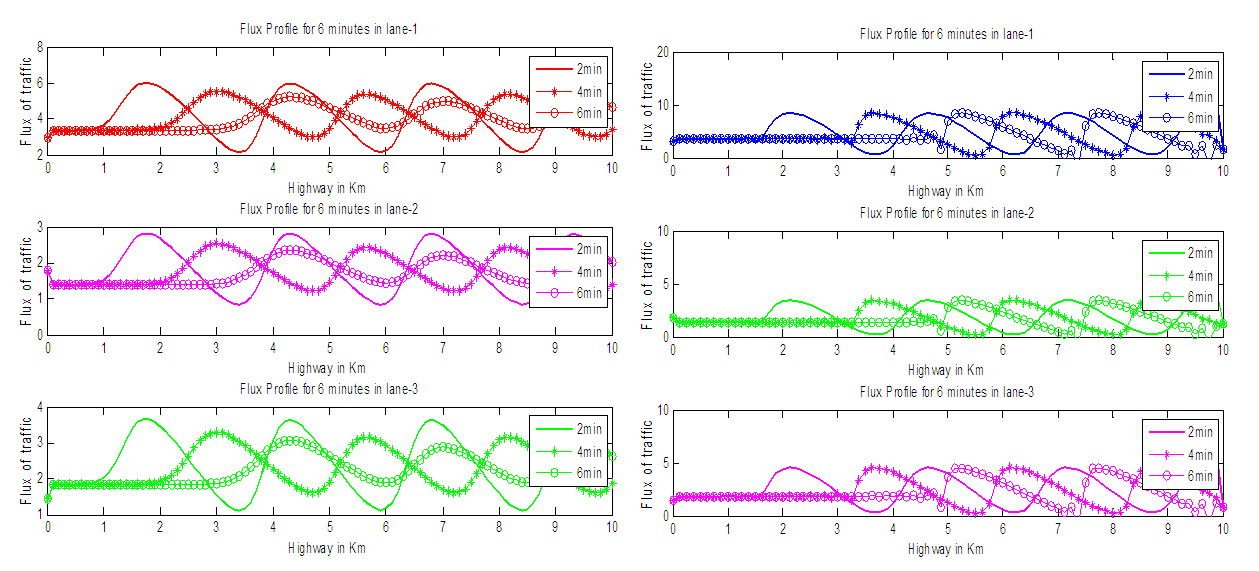Figure 4. Flux profile of EUDS and LWDS

The velocity also is plotted with respect to the density in the following figure 5 using linear velocity-density functions. Here, we conclude that the velocity and density relationship is linear which agrees accurately with our assumptions.

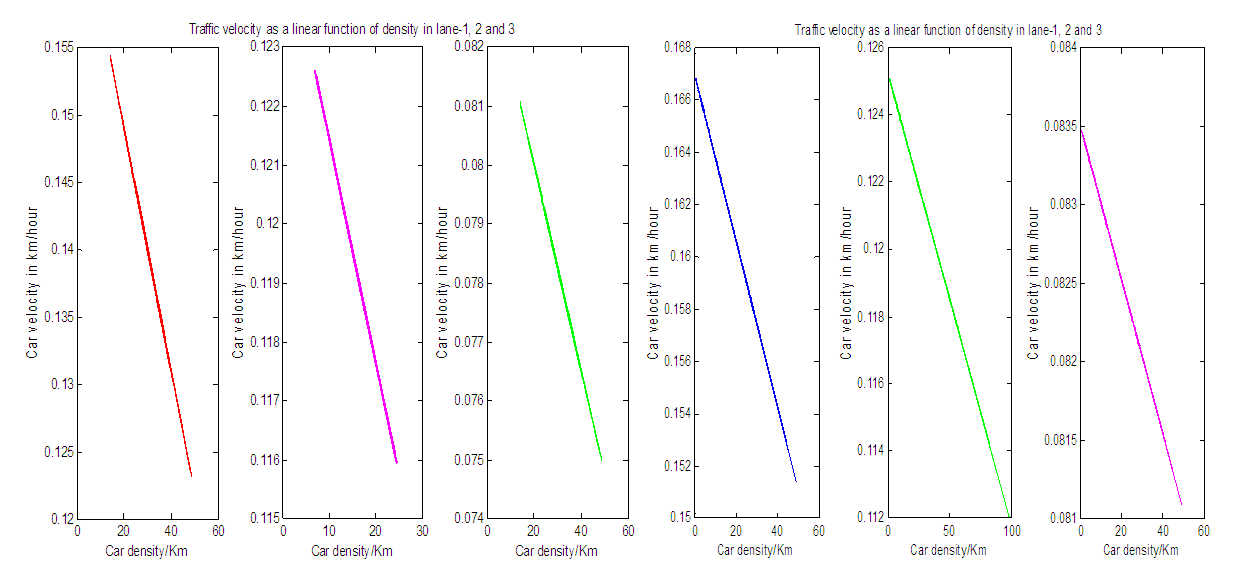Figure 5. Traffic velocity as a linear function of density in case of EUDS and LWDS

In total traffic density we add the computed density of three lanes which is presented in figure 6 according to the distance. The total density of three lanes agrees with density profile for single lane traffic flow model as in same.

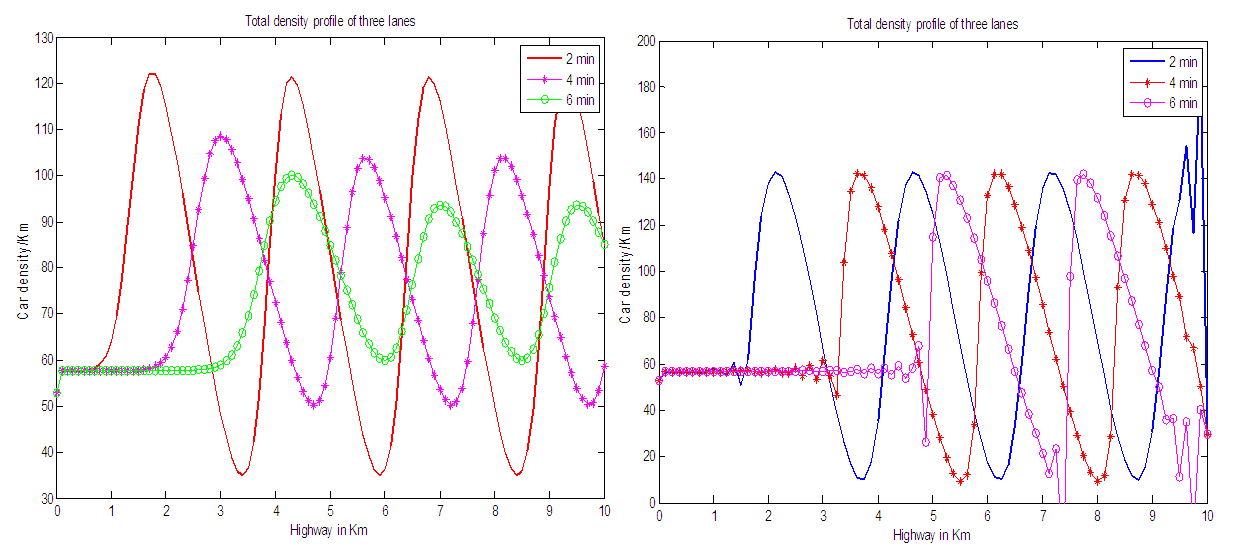Figure 6. Total density profile of three lanes in case of EUDS and LWDS

The numerical solution converges for decreasing temporal and spatial grid sizes, which is very good qualitative behavior of the numerical solution of multilane traffic flow model for three lanes.

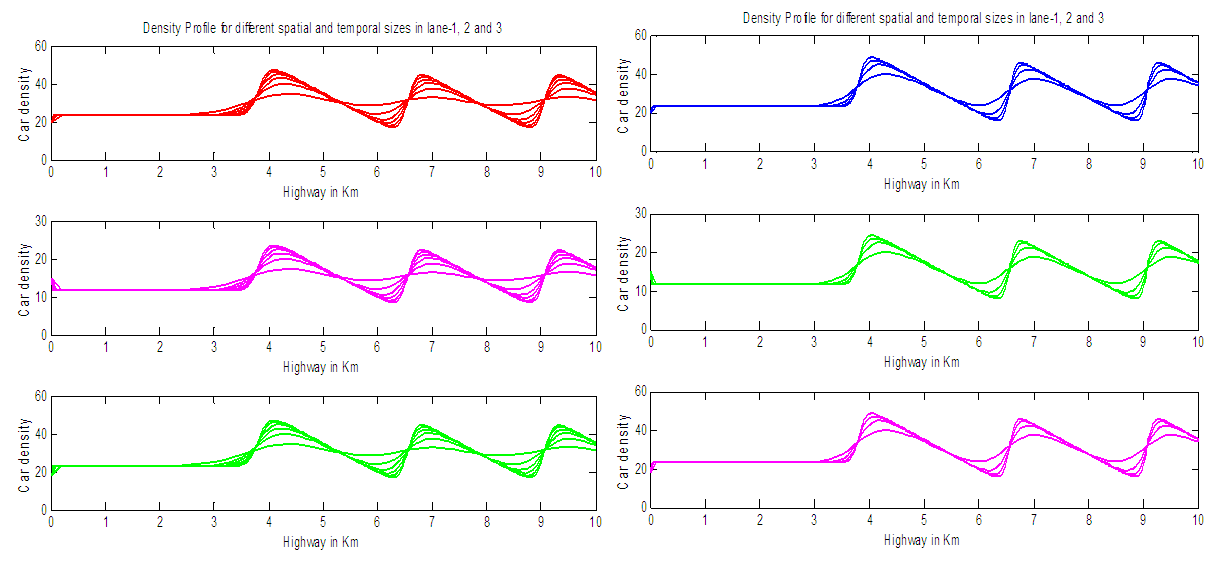Figure 7. Density Profile for different spatial and temporal step sizes using EUDS and LWDS

6. Conclusions

We have shown that the numerical result based on the explicit finite difference scheme and Lax-Wendroff difference scheme agrees with basic some qualitative behavior of multilane traffic flow model for three lanes. This qualitative behavior agreement verified the implementation of numerical schemes for the multilane traffic flow model with sufficient accuracy. Also we present that the sum of the flow of three lanes is in same nature as the flow of the single lane traffic flow model. Finally we have shown that the numerical solution converges for decreasing temporal and spatial grid sizes where the rate of convergence of LWDS is higher than EUDS.