-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2021; 11(2): 21-22
doi:10.5923/j.am.20211102.02
Received: Jun. 14, 2021; Accepted: Jul. 11, 2021; Published: Jul. 15, 2021

A P-Series Formula
Ameha Tefera Tessema
Commercial Bank of Ethiopia, Addis Ababa, Ethiopia
Correspondence to: Ameha Tefera Tessema, Commercial Bank of Ethiopia, Addis Ababa, Ethiopia.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Let 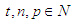 such that
such that 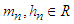 then
then 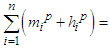
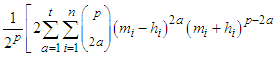
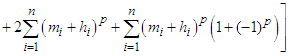 Where p=2t+1 for all p odd Natural numbers(N), p=2t+2 for all p even natural numbers(N).
Where p=2t+1 for all p odd Natural numbers(N), p=2t+2 for all p even natural numbers(N).
Keywords: Power series, Formula
Cite this paper: Ameha Tefera Tessema, A P-Series Formula, Applied Mathematics, Vol. 11 No. 2, 2021, pp. 21-22. doi: 10.5923/j.am.20211102.02.
Article Outline
1. Introduction
- In the early time fermat, a French number theorist, had stated that the equation
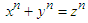 has no solution in integers, if n>2 [1]. The problem to find the exact value of z is enhanced as the number of terms increases rather than power two. Let us have n terms each of which has a common power p in the series then the series is called a p-series which is applied by the following theorem for p>2 which is also an answer for the claim of fermat.Theorem 1. Let
has no solution in integers, if n>2 [1]. The problem to find the exact value of z is enhanced as the number of terms increases rather than power two. Let us have n terms each of which has a common power p in the series then the series is called a p-series which is applied by the following theorem for p>2 which is also an answer for the claim of fermat.Theorem 1. Let 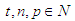 such that
such that 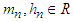 then
then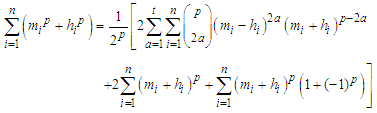 Where p=2t+1 for all p odd Natural numbers(N), p=2t+2 for all p even natural numbers.Proof. Let
Where p=2t+1 for all p odd Natural numbers(N), p=2t+2 for all p even natural numbers.Proof. Let  such that
such that  if
if  where
where 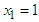 then multiplying
then multiplying 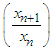 up to n times we get
up to n times we get 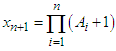 , therefor we can write this expression to p power as
, therefor we can write this expression to p power as 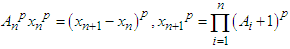 If the binomial theorem for expansion
If the binomial theorem for expansion 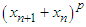 .Can be written as
.Can be written as 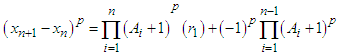 Where
Where 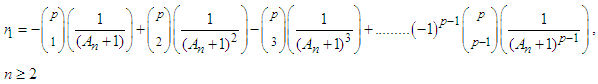 , Putting
, Putting 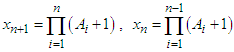 and dividing both sides by
and dividing both sides by 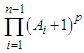 we get
we get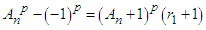 | (1) |
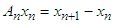 is
is 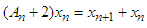 which can be written to p power as
which can be written to p power as 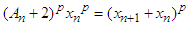 If binomial theorem for expansion
If binomial theorem for expansion 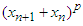 can be written as
can be written as 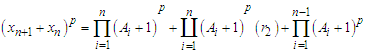 Where
Where 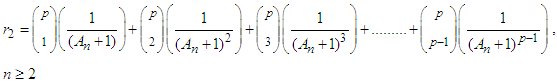 ,Putting
,Putting 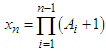 in
in 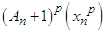 and dividing both sides by
and dividing both sides by 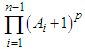 we get
we get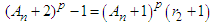 | (2) |
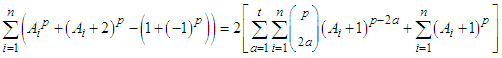 Where p=2t+1 for all p odd natural numbers, whereas p=2t+2 for all p even natural numbersLet put
Where p=2t+1 for all p odd natural numbers, whereas p=2t+2 for all p even natural numbersLet put 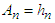 and if
and if 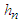 be divided by
be divided by 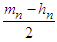 such that
such that 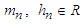 (Real numbers) then we get the following result
(Real numbers) then we get the following result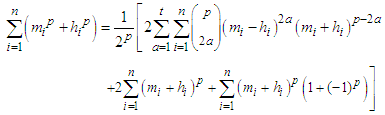 This result led us to a conclusion that every couple terms which have common power can undergo this formula.
This result led us to a conclusion that every couple terms which have common power can undergo this formula. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML