-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2021; 11(1): 12-14
doi:10.5923/j.am.20211101.03
Received: Apr. 8, 2021; Accepted: Apr. 24, 2021; Published: Apr. 26, 2021

A Short Note on Converting a Series into a Form of Fraction
Ameha Tefera Tessema
Strategic Planning, Commercial Bank of Ethiopia, Addis Ababa, Ethiopia
Correspondence to: Ameha Tefera Tessema, Strategic Planning, Commercial Bank of Ethiopia, Addis Ababa, Ethiopia.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Let for all 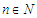 and
and 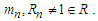 If the sum of a series defined as
If the sum of a series defined as 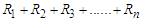 and if
and if 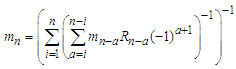 where
where 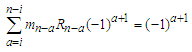 for n=i,
for n=i, 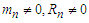 ,
,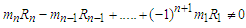 then the sum of a series can be converted into fraction as follows
then the sum of a series can be converted into fraction as follows 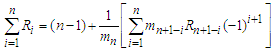 .
.
Keywords: Fractional series, Continued fraction, Series
Cite this paper: Ameha Tefera Tessema, A Short Note on Converting a Series into a Form of Fraction, Applied Mathematics, Vol. 11 No. 1, 2021, pp. 12-14. doi: 10.5923/j.am.20211101.03.
1. Introduction
- Continued fraction can be defined as dividing the numerator by successive real numbers. Continues fraction algorism is a general factoring method which has received a great deal of attention in recent years and in order to implement it on a highly parallel computer, like the massively parallel processor, it is necessary to be able to compute certain numbers which occur at widely-spaced intervals within the continued fraction expansion of
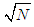 where N is the number to be factored [8]. The Massively Parallel Processor (MPP) is a highly parallel scientific computer which was originally intended for image processing and analysis applications but it is also suitable for a large range of other scientific applications [6]. Continued fractions are used in analysing Frieze patterns [5], in R_dseth's formula for Frobenius numbers [2], in computing the Jacobi symbol [4], in stream ciphers [1], in pseudo-random number generators [7], in cryptanalysis of the RSA public-key cryptosystem with small private exponents [3]. There are numerous beautiful continued fractions developed by Euler, Lagrange, Gauss, Stieltjes, Ramanujan and so on using various methods. However, according to this paper the sum of real numbers can be written as
where N is the number to be factored [8]. The Massively Parallel Processor (MPP) is a highly parallel scientific computer which was originally intended for image processing and analysis applications but it is also suitable for a large range of other scientific applications [6]. Continued fractions are used in analysing Frieze patterns [5], in R_dseth's formula for Frobenius numbers [2], in computing the Jacobi symbol [4], in stream ciphers [1], in pseudo-random number generators [7], in cryptanalysis of the RSA public-key cryptosystem with small private exponents [3]. There are numerous beautiful continued fractions developed by Euler, Lagrange, Gauss, Stieltjes, Ramanujan and so on using various methods. However, according to this paper the sum of real numbers can be written as 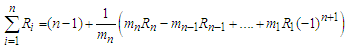 where
where 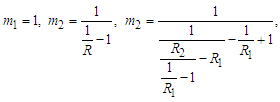 and so on.Still nowadays there is no any stated general formula which serves to transform every kind of series into a form of fraction since the formulas existed function valid only for specific values of rational integers. However, on this paper I want to show that how every kind of series can be converted into a form of fraction. Transforming a series into a form of fraction will help to solve various mathematical problems since any series can be converted into fractional series or rational fraction series. Since rational function, which can be defined by rational fraction, can be used in the series, converting a series into form of fraction can be used to approximate or model more complex equations in science and engineering including fields and forces in physics, spectroscopy in analytical chemistry, enzyme kinetics in biochemistry, electronic circuitry, aerodynamics, medicine concentrations in vivo, wave functions for atoms and molecules, optics and photography to improve image resolution, and acoustics and sound [9].Theorem 1: Let for all
and so on.Still nowadays there is no any stated general formula which serves to transform every kind of series into a form of fraction since the formulas existed function valid only for specific values of rational integers. However, on this paper I want to show that how every kind of series can be converted into a form of fraction. Transforming a series into a form of fraction will help to solve various mathematical problems since any series can be converted into fractional series or rational fraction series. Since rational function, which can be defined by rational fraction, can be used in the series, converting a series into form of fraction can be used to approximate or model more complex equations in science and engineering including fields and forces in physics, spectroscopy in analytical chemistry, enzyme kinetics in biochemistry, electronic circuitry, aerodynamics, medicine concentrations in vivo, wave functions for atoms and molecules, optics and photography to improve image resolution, and acoustics and sound [9].Theorem 1: Let for all 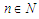 and
and 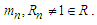 If the sum of a series defined as
If the sum of a series defined as 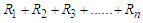 and if
and if 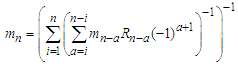 where
where 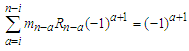 for n=i
for n=i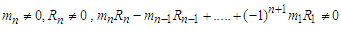 then the sum of a series can be converted into fraction as follows
then the sum of a series can be converted into fraction as follows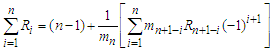 Proof. Suppose
Proof. Suppose 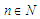 and
and 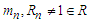 such that
such that 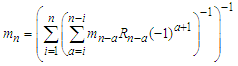 where
where 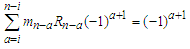 for n=i
for n=i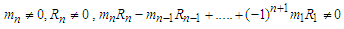 and
and 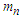 can be calculated as follows
can be calculated as follows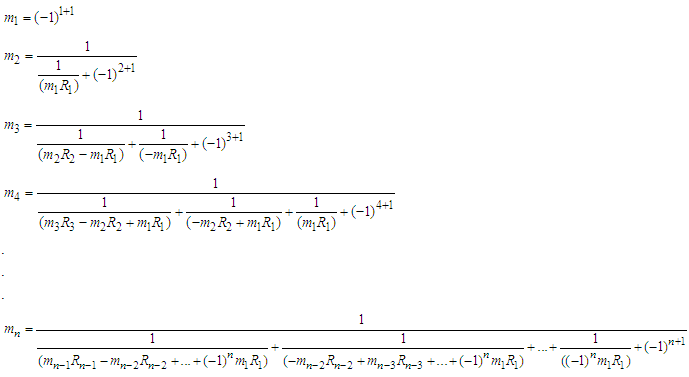 The sum of real numbers can be represented as
The sum of real numbers can be represented as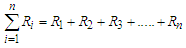 which can also calculate as follows
which can also calculate as follows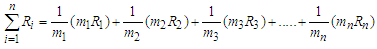 In order to get cancellation one, split the terms in brackets in the following form
In order to get cancellation one, split the terms in brackets in the following form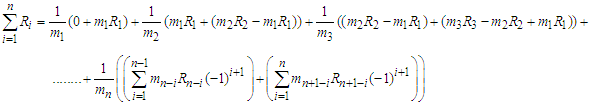 Collecting like terms, we have the following series
Collecting like terms, we have the following series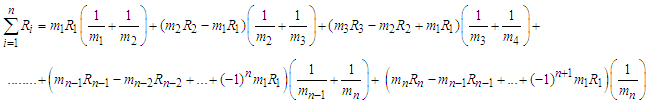 And putting the value of
And putting the value of 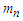 in the above series, we have
in the above series, we have 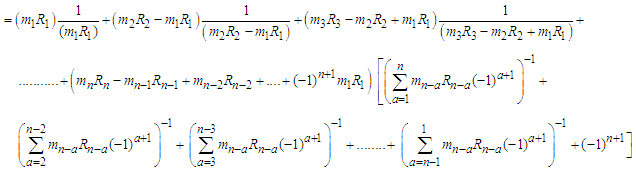 Thus we have a series converted in the form of fraction as follow
Thus we have a series converted in the form of fraction as follow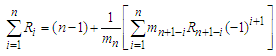
2. Conclusions
- Since
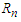 is arbitrary real number, the sum of
is arbitrary real number, the sum of 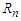 can be represented as a form of fraction. The difference between consecutive fractional terms,
can be represented as a form of fraction. The difference between consecutive fractional terms, 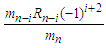 where i=0,1,2,…., diminishes without limit for each
where i=0,1,2,…., diminishes without limit for each 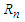 is divided by
is divided by 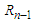 up to
up to 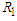 and since the form of fraction are finite in number, the fraction is said to be definite. Therefor the formula developed by this paper serves as a general formula to convert every kind of series into a form of fraction.
and since the form of fraction are finite in number, the fraction is said to be definite. Therefor the formula developed by this paper serves as a general formula to convert every kind of series into a form of fraction.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML