Mousumi Datta, Md. Shah Alam, Umme Hahiba, Nigar Sultana, Md. Babul Hossain
Department of Mathematics, Mawlana Bhashani Science and Technology University, Santosh, Tangail, Bangladesh
Correspondence to: Md. Shah Alam, Umme Hahiba, Nigar Sultana, Md. Babul Hossain, Department of Mathematics, Mawlana Bhashani Science and Technology University, Santosh, Tangail, Bangladesh.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This article explores a new approach to achieving an exact solution of a special type of both linear and non-linear partial differential equation (LNLPDE) with mixture derivatives, namely Goursat problems by Double Elzaki Decomposition Method (DEDM). The process utilizes characteristics of Double Elzaki Transform and Adomian Polynomials to obtain an exact solution for Goursat problems. Moreover, Adomian polynomials are used to decompose the non-linear terms. The findings indicate the proposed method is very easy to use and more effective than other techniques because of seed and computational time. It can easily be expanded to other mixed-type LNLPDEs and the approximation task size can be simplified.
Keywords:
Linear and Non-linear PDEs, Double Elzaki Transform, Mixed Partial Derivatives, Adomian Polynomials, Goursat Problem
Cite this paper: Mousumi Datta, Md. Shah Alam, Umme Hahiba, Nigar Sultana, Md. Babul Hossain, Exact Solution of Goursat Problem with Linear and Non-linear Partial Differential Equations by Double Elzaki Decomposition Method, Applied Mathematics, Vol. 11 No. 1, 2021, pp. 5-11. doi: 10.5923/j.am.20211101.02.
1. Introduction
LNLPDE describes many problems in different fields of applied mathematics and sciences. These equations arise in various scientific models such as the fluid dynamics, chemical reaction-diffusion, shallow water wave propagation, and Schrodinger wave equation models. LNLDEs naturally occurs in various fields of study such as in engineering, physics, and applied mathematics. Many mathematicians and scientists have drawn too much attention to the extensive effectiveness of these equations. In the analysis of physical phenomena and applied sciences, the Goursat partial differential equation occurs in LNLPDEs including mixed-type derivatives and it is known as hyperbolic PDE of second order. The standard form of the Goursat problems with conditions [7-10] is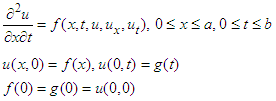 Several computational techniques, such as Variation Iteration Method (VIM) [7], Laplace Substitution–Variational Iteration Method (LSVIM) [15], Adomian Decomposition Method (ADM) [11], Two-Dimensional Differential Transform Method (DTM) [8], Modified Variational Iteration Methods [12], Runge-Kutta Method [10] and Finite Difference Method (FDM) [13] and Homotopy Analysis Method (HAM) [14] have been developed to resolve the linear and nonlinear form of Goursat Problems. Previously, the ESM was used [16-17] to solve second-order linear and non-linear PDEs containing mixed partial derivatives. Recently, inspired and encouraged by research work in these fields, we introduce a new method named DEDM, based on Elzaki transform [1] and Double Elzaki Transform [2-6]. The proposed technique is combined the Double Elzaki Transform with the Adomian polynomials for solving non-linear Goursat problems. Here in section (2), definitions and partial derivatives of the Double Elzaki transform will be described. In Section (3), explanation of main advantage of DEDM applied directly without linearization or interruption to Goursat problems are presented. To clarify the applicability and effectiveness of the proposed method for several linear and non-linear problems are presented in section (4). We finally conclude the result at last section.
Several computational techniques, such as Variation Iteration Method (VIM) [7], Laplace Substitution–Variational Iteration Method (LSVIM) [15], Adomian Decomposition Method (ADM) [11], Two-Dimensional Differential Transform Method (DTM) [8], Modified Variational Iteration Methods [12], Runge-Kutta Method [10] and Finite Difference Method (FDM) [13] and Homotopy Analysis Method (HAM) [14] have been developed to resolve the linear and nonlinear form of Goursat Problems. Previously, the ESM was used [16-17] to solve second-order linear and non-linear PDEs containing mixed partial derivatives. Recently, inspired and encouraged by research work in these fields, we introduce a new method named DEDM, based on Elzaki transform [1] and Double Elzaki Transform [2-6]. The proposed technique is combined the Double Elzaki Transform with the Adomian polynomials for solving non-linear Goursat problems. Here in section (2), definitions and partial derivatives of the Double Elzaki transform will be described. In Section (3), explanation of main advantage of DEDM applied directly without linearization or interruption to Goursat problems are presented. To clarify the applicability and effectiveness of the proposed method for several linear and non-linear problems are presented in section (4). We finally conclude the result at last section.
2. Preliminaries
2.1. Elzaki Transform
The Elzaki transform for exponential order of function f, in the set A is defined by: 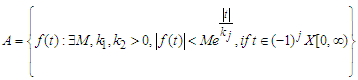 | (1) |
where M is a finite constant and 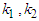 are finite or infinite in set A.The Elzaki transform symbolized by the operator E (.) and expressed by the integral equation-
are finite or infinite in set A.The Elzaki transform symbolized by the operator E (.) and expressed by the integral equation-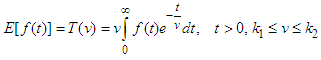 | (2) |
where 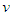 is used to factor the variable
is used to factor the variable 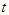 in the argument of function
in the argument of function 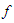 .
.Table 1
 |
| |
|
2.2. Inverse Elzaki Transform
If 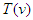 is the Elzaki transforms of
is the Elzaki transforms of 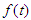 then
then 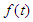 is called the inverse Elzaki transform of
is called the inverse Elzaki transform of 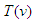 and in mathematical terms, it can be expressed as
and in mathematical terms, it can be expressed as 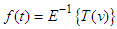 , where
, where 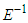 is an operator and is called inverse Elzaki transform.
is an operator and is called inverse Elzaki transform.
2.3. Double Elzaki Transform
The function 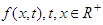 which can be expressed as an infinite convergent series, as a consequence Double Elzaki Transform is:
which can be expressed as an infinite convergent series, as a consequence Double Elzaki Transform is: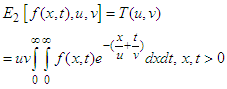 | (3) |
where 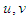 are complex.
are complex. Table 2
 |
| |
|
2.4. Partial Derivatives of Double Elzaki Transform
Using Integration by parts to produce double Elzaki transforms of partial derivatives of 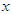 and
and 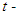
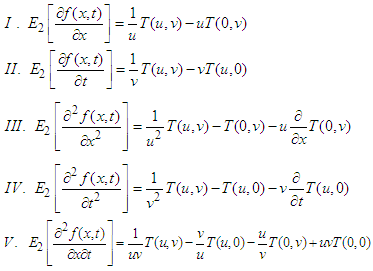 Proof: By the definition of double Elzaki transform-
Proof: By the definition of double Elzaki transform-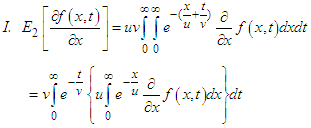 Using first partial derivatives of Elzaki transform, the inner integral provides
Using first partial derivatives of Elzaki transform, the inner integral provides 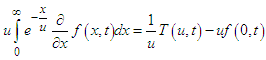 Therefore,
Therefore, 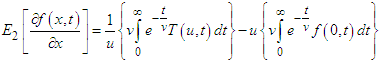 Taking Elzaki transform with respect to
Taking Elzaki transform with respect to  the above integrals is converted to
the above integrals is converted to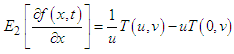
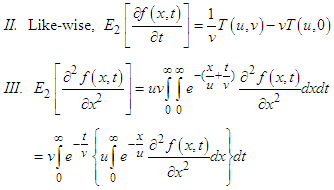 By second order partial derivatives of Elzaki transform, the inner integral becomes-
By second order partial derivatives of Elzaki transform, the inner integral becomes- 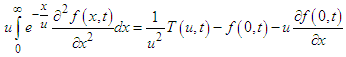 Therefore,
Therefore, 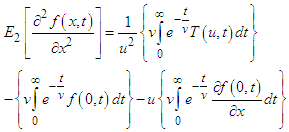 Taking Elzaki transform with respect to
Taking Elzaki transform with respect to 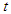
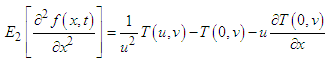 IV. Similarly the following formula can be established
IV. Similarly the following formula can be established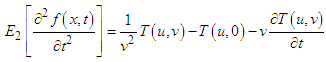
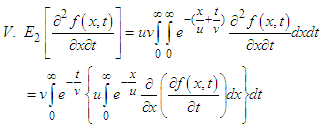 The inner integral reduces to
The inner integral reduces to 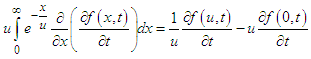 Therefore,
Therefore, 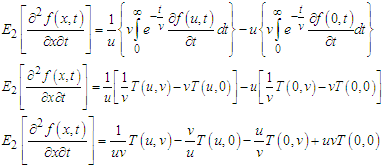
3. DEDM for Goursat Problem
In order to explain the solution procedure for DEDM, considering a general Goursat problem rolling mixed partial derivatives with conditions is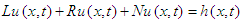 | (4) |
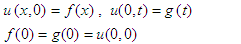 | (5) |
where 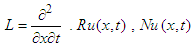 and
and 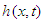 are linear term, non-linear differential term and source term respectively.Consequently, equation (4) becomes-
are linear term, non-linear differential term and source term respectively.Consequently, equation (4) becomes- 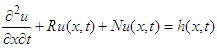 By double Elzaki transform the above equation is converted to-
By double Elzaki transform the above equation is converted to-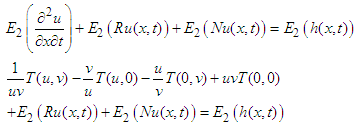 | (6) |
Again taking single Elzaki transform in equation (5), then the equation reduces to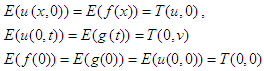 | (7) |
Substituting these values in equation (6), implies that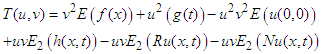 Now, on both sides of the above equation using inverse double Elzaki transform, finally-
Now, on both sides of the above equation using inverse double Elzaki transform, finally-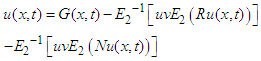 | (8) |
where initial conditions are prescribed and 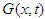 reflects the resulting source term.Consider an infinite series solution to solve non-linear mixed type PDEs by DEDM is
reflects the resulting source term.Consider an infinite series solution to solve non-linear mixed type PDEs by DEDM is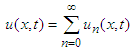 | (9) |
Then the non-linear term is reduced to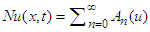 | (10) |
where 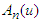 are Adomian polynomials with components
are Adomian polynomials with components 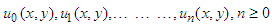 are defined by
are defined by 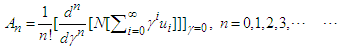 | (11) |
Substituting u(x, y) and Nu(x, y) in equation (8), the equation is converted to-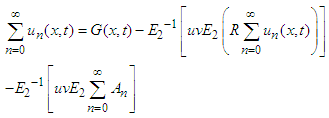 | (12) |
Comparing on both sides of the above equation, obtained relationships are 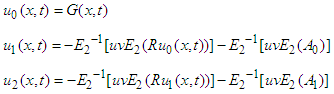 In general, the recursive relations are
In general, the recursive relations are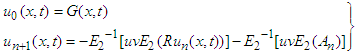 The values of all
The values of all 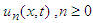 are obtained from the above recursive relation and substitute in equation (9), then the series solution for the given equation is found.
are obtained from the above recursive relation and substitute in equation (9), then the series solution for the given equation is found.
4. Applications
The DEDM for LNLPDEs with mixed type derivatives will be explained by considering Goursat problems in a linear and non-linear form.
4.1. Linear Homogeneous Goursat Problem
Considering a Goursat problem which is linear and homogeneous 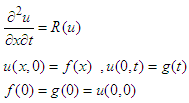 where,
where, 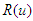 is a function of first degree.Example 1: Considering a Goursat problem which is linear and homogeneous-
is a function of first degree.Example 1: Considering a Goursat problem which is linear and homogeneous- 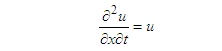 | (13) |
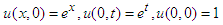 | (14) |
Equation (13) is converted to this new one by double Elzaki transform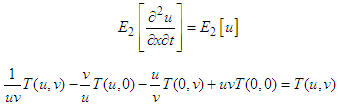 | (15) |
Operating single Elzaki transform, equation (14) reduces to 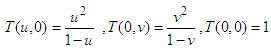 Using the above initial values, the equation (15) is reduced to-
Using the above initial values, the equation (15) is reduced to- 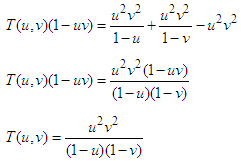 The exact solution is found by using inverse double Elzaki transform
The exact solution is found by using inverse double Elzaki transform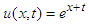 which is verified by the results obtained by VIM and ADM.
which is verified by the results obtained by VIM and ADM.
4.2. Linear Non-Homogeneous Goursat Problem
Consider a Goursat problem which is linear and non-homogeneous- 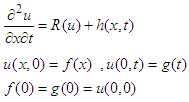 Where
Where 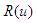 is a function of first degree.Example 2: Considering linear non-homogeneous Goursat problem-
is a function of first degree.Example 2: Considering linear non-homogeneous Goursat problem- 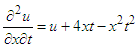 | (16) |
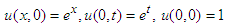 | (17) |
Taking double Elzaki transform in equation (16) 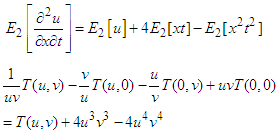 | (18) |
By single Elzaki transform equation (17) becomes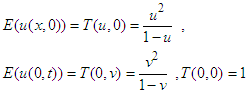 with the above conditions, the equation (18) is converted to
with the above conditions, the equation (18) is converted to 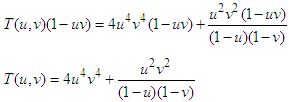 Applying inverse double Elzaki transform in the above equation
Applying inverse double Elzaki transform in the above equation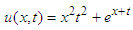 Which is the required exact solution. This result is completely similar with the result obtained by VIM and DTM.
Which is the required exact solution. This result is completely similar with the result obtained by VIM and DTM.
4.3. Non-linear Goursat Problem
To illustrate the proposed DEDM, two non-linear homogeneous and non-homogeneous Goursat problem is considered.Example 3: Considering the non- linear non-homogeneous Goursat problem 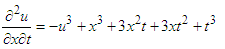 | (19) |
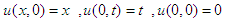 | (20) |
Directly use the double Elzaki transform in equation (19) implies that 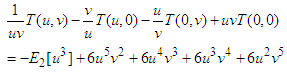 Applying single Elzaki transform in equation (20), conditions reduce to
Applying single Elzaki transform in equation (20), conditions reduce to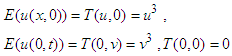 The transformed equation reduces with these conditions as
The transformed equation reduces with these conditions as 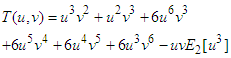 Again apply inverse double Elzaki transform in the above equation on both sides,
Again apply inverse double Elzaki transform in the above equation on both sides, 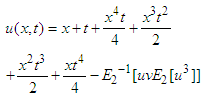 | (21) |
In DEDM, solution is represented in infinite series form as below,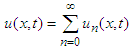 | (22) |
And the non-linear term can be written as follows, 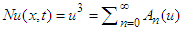 | (23) |
where 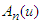 are Adomian polynomials of components
are Adomian polynomials of components 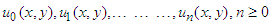 which is defined by the formula (11).Some Adomian polynomials of
which is defined by the formula (11).Some Adomian polynomials of 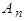 are found as
are found as 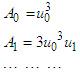 Then the equation (21) is transformed to
Then the equation (21) is transformed to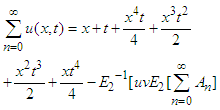 The following recursive relation is found by comparing the above equation on both sides,
The following recursive relation is found by comparing the above equation on both sides, 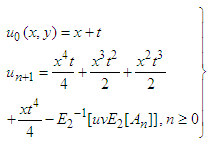 The following few components of un (x, y), n>0 are determined from the above relation
The following few components of un (x, y), n>0 are determined from the above relation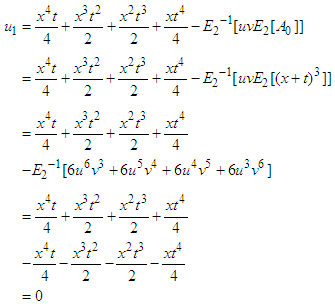 Consequently,
Consequently, 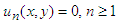 Substituting all values of un (x, y), n≥0 in equation (22), finally the series solution of the given equation is
Substituting all values of un (x, y), n≥0 in equation (22), finally the series solution of the given equation is 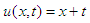 This results are in complete compliance with the result given by VIM and DTM.Example 4: Consider the non-linear homogeneous Goursat problem
This results are in complete compliance with the result given by VIM and DTM.Example 4: Consider the non-linear homogeneous Goursat problem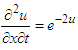 | (24) |
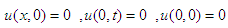 | (25) |
Applying double Elzaki transform the equation (24) becomes- 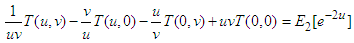 Using the single Elzaki transform the conditions in equation (25) reduces to
Using the single Elzaki transform the conditions in equation (25) reduces to 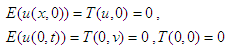 with these new conditions the above equation gives
with these new conditions the above equation gives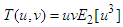 Operating inverse double Elzaki transform, find that
Operating inverse double Elzaki transform, find that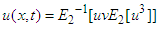 | (26) |
The infinite series solution in DEDM is presented by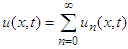 | (27) |
and the non-linear term can be written as-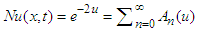 | (28) |
where 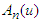 are Adomian polynomials of components
are Adomian polynomials of components 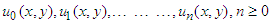 which is defined by the formula (11). Adomian polynomials
which is defined by the formula (11). Adomian polynomials 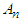 are
are 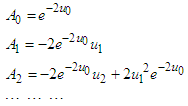 Then the equation (26) becomes
Then the equation (26) becomes 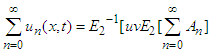 The recursive relationships are obtained by comparing both sides of the above equation
The recursive relationships are obtained by comparing both sides of the above equation 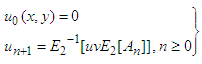 The following new components of
The following new components of 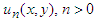 have been found from the above relationship.
have been found from the above relationship.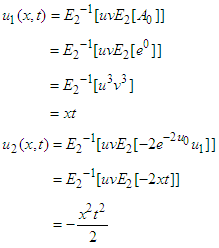 Like-wise
Like-wise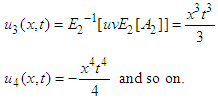 Putting all values of un (x, y), n≥0 in equation (27), finally the series solution of the given equation is
Putting all values of un (x, y), n≥0 in equation (27), finally the series solution of the given equation is 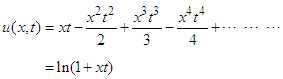 This finding is in complete compliance with the result obtained by VIM and DTM.
This finding is in complete compliance with the result obtained by VIM and DTM.
5. Conclusions
To find the approximate series solutions we successfully implemented the DEDM of linear and non-linear Goursat problems. The mentioned process eliminates the computational difficulties that occur in other existing methods and is directly implemented without the use of linearization, transformation, discretization or limiting assumptions. By applying DEDM, many examples of linear and non-linear Goursat problems were evaluated and the findings have shown noticeable and more satisfactory results. The improvement of this methodology would lead to the possibility of increasing the order and accuracy of the system further.
References
| [1] | Elzaki, T. M. (2011). Application of new transform “Elzaki transform” to partial differential equations. Global Journal of pure and applied Mathematics, 7(1), 65-70. |
| [2] | Hassaballa, A. A., & Salih, Y. A. (2015). On Double Elzaki Transform and Double Laplace Transform. IOSR Journal of Mathematics (IOSR-JM), 11(1), 35-41. |
| [3] | Elzaki, T. M., Hilal, E. M., Arabia, J. S., & Arabia, J. S. (2012). Solution of Telegraph Equation by Modified of Double Sumudu Transform" Elzaki Transform. Mathematical Theory and Modeling, 2(4), 95-103. |
| [4] | Idrees, M. I., Ahmed, Z., Awais, M., & Perveen, Z. (2018). On the convergence of double Elzaki transform. Int Journal of Advanced and Applied Sciences, 5(6), 19-24. |
| [5] | Hassan, M. A. (2020). Double Elzaki Transform Decomposition Method for Solving Non-Linear Partial Differential Equations. Journal of Applied Mathematics and Physics, 8(8), 1463-1471. |
| [6] | MAHGOB, M. (2015). Solution of partial integro-differential equations by double Elzaki transform method. Mathematical Theory and Modeling, 5(5), 61-65. |
| [7] | Wazwaz, A. M. (2007). The variational iteration method for a reliable treatment of the linear and the nonlinear Goursat problem. Applied Mathematics and Computation, 193(2), 455-462. |
| [8] | Taghvafard, H., & Erjaee, G. H. (2010). Two-dimensional differential transform method for solving linear and non-linear Goursat problem. International Journal for Engineering and Mathematical Sciences, 6(2), 103-106. |
| [9] | Wazwaz, A. M. (1995). The decomposition method for approximate solution of the Goursat problem. Applied Mathematics and Computation, 69(2-3), 299-311. |
| [10] | Day, J. T. (1966). A Runge-Kutta method for the numerical solution of the Goursat problem in hyperbolic partial differential equations. The Computer Journal, 9(1), 81-83. |
| [11] | Ahmad J, Mushtaq M. (2015). Exact Solution of Linear and Non-linear Day, J. T. (1966). A Runge-Kutta method for the numerical solution of the Goursat problem in hyperbolic partial differential equations. The Computer Journal, 9(1), 81-83. Goursat Problems. Univers J Comput Math. 3 (1): 14-17. |
| [12] | Noor, M. A., & Mohyud-Din, S. T. (2008). Modified variational iteration method for Goursat and Laplace problems. World Applied Sciences Journal, 4(4), 487-498. |
| [13] | Pandey, P. K. (2014). A Finite Difference Method for Numerical Solution of Goursat Problem of Partial Differential Equation. Open Access Libr J, 1, 1-6. |
| [14] | Usman M, Zubair T, Ali U, Mohyud-din ST. (2012). On Goursat Problems. Int J Mod Math Sci.3 (3): 63-76. |
| [15] | Al-Fayadh, A., & Faraj, D. S. (2019). Laplace Substitution–Variational Iteration Method for Solving Goursat Problems Involving Mixed Partial Derivatives. American Journal of Mathematical and Computer Modelling, 4(1), 16-20. |
| [16] | Hossain, M. B. & Datta, M. (2018). Solutions of Linear Partial Differential Equations with Mixed Partial Derivatives by Elzaki Substitution Method. American Journal of Computational and Applied Mathematics 8:59-64. |
| [17] | Datta, M., Habiba, U., & Hossain, M. B. (2020). Elzaki Substitution Method for Solving Nonlinear Partial Differential Equations with Mixed Partial Derivatives Using Adomain Polynomial. International Journal, 8(1), 6-12. |



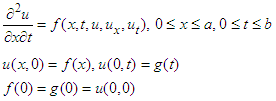 Several computational techniques, such as Variation Iteration Method (VIM) [7], Laplace Substitution–Variational Iteration Method (LSVIM) [15], Adomian Decomposition Method (ADM) [11], Two-Dimensional Differential Transform Method (DTM) [8], Modified Variational Iteration Methods [12], Runge-Kutta Method [10] and Finite Difference Method (FDM) [13] and Homotopy Analysis Method (HAM) [14] have been developed to resolve the linear and nonlinear form of Goursat Problems. Previously, the ESM was used [16-17] to solve second-order linear and non-linear PDEs containing mixed partial derivatives. Recently, inspired and encouraged by research work in these fields, we introduce a new method named DEDM, based on Elzaki transform [1] and Double Elzaki Transform [2-6]. The proposed technique is combined the Double Elzaki Transform with the Adomian polynomials for solving non-linear Goursat problems. Here in section (2), definitions and partial derivatives of the Double Elzaki transform will be described. In Section (3), explanation of main advantage of DEDM applied directly without linearization or interruption to Goursat problems are presented. To clarify the applicability and effectiveness of the proposed method for several linear and non-linear problems are presented in section (4). We finally conclude the result at last section.
Several computational techniques, such as Variation Iteration Method (VIM) [7], Laplace Substitution–Variational Iteration Method (LSVIM) [15], Adomian Decomposition Method (ADM) [11], Two-Dimensional Differential Transform Method (DTM) [8], Modified Variational Iteration Methods [12], Runge-Kutta Method [10] and Finite Difference Method (FDM) [13] and Homotopy Analysis Method (HAM) [14] have been developed to resolve the linear and nonlinear form of Goursat Problems. Previously, the ESM was used [16-17] to solve second-order linear and non-linear PDEs containing mixed partial derivatives. Recently, inspired and encouraged by research work in these fields, we introduce a new method named DEDM, based on Elzaki transform [1] and Double Elzaki Transform [2-6]. The proposed technique is combined the Double Elzaki Transform with the Adomian polynomials for solving non-linear Goursat problems. Here in section (2), definitions and partial derivatives of the Double Elzaki transform will be described. In Section (3), explanation of main advantage of DEDM applied directly without linearization or interruption to Goursat problems are presented. To clarify the applicability and effectiveness of the proposed method for several linear and non-linear problems are presented in section (4). We finally conclude the result at last section.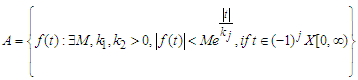
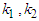 are finite or infinite in set A.The Elzaki transform symbolized by the operator E (.) and expressed by the integral equation-
are finite or infinite in set A.The Elzaki transform symbolized by the operator E (.) and expressed by the integral equation-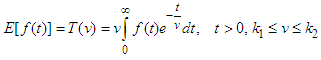
 is used to factor the variable
is used to factor the variable 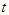 in the argument of function
in the argument of function 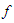 .
.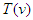 is the Elzaki transforms of
is the Elzaki transforms of 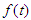 then
then 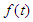 is called the inverse Elzaki transform of
is called the inverse Elzaki transform of 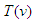 and in mathematical terms, it can be expressed as
and in mathematical terms, it can be expressed as 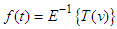 , where
, where 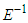 is an operator and is called inverse Elzaki transform.
is an operator and is called inverse Elzaki transform.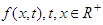 which can be expressed as an infinite convergent series, as a consequence Double Elzaki Transform is:
which can be expressed as an infinite convergent series, as a consequence Double Elzaki Transform is: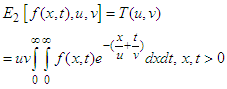
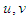 are complex.
are complex. 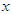 and
and 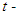
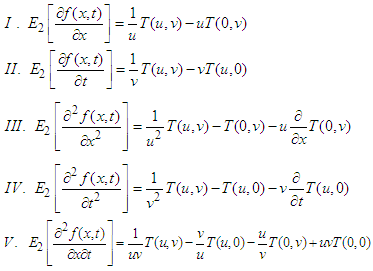 Proof: By the definition of double Elzaki transform-
Proof: By the definition of double Elzaki transform-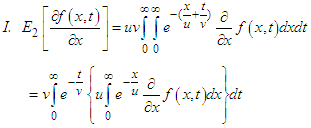 Using first partial derivatives of Elzaki transform, the inner integral provides
Using first partial derivatives of Elzaki transform, the inner integral provides 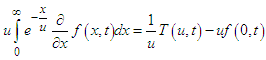 Therefore,
Therefore, 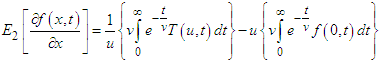 Taking Elzaki transform with respect to
Taking Elzaki transform with respect to 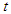 the above integrals is converted to
the above integrals is converted to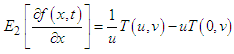
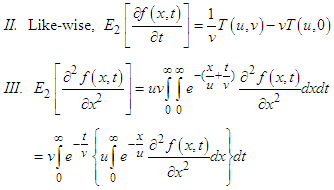 By second order partial derivatives of Elzaki transform, the inner integral becomes-
By second order partial derivatives of Elzaki transform, the inner integral becomes- 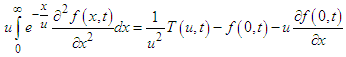 Therefore,
Therefore, 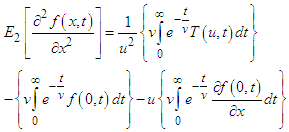 Taking Elzaki transform with respect to
Taking Elzaki transform with respect to 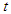
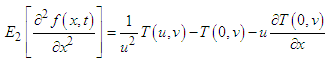 IV. Similarly the following formula can be established
IV. Similarly the following formula can be established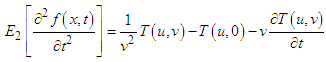
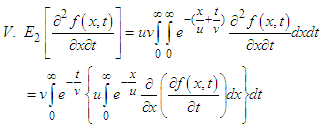 The inner integral reduces to
The inner integral reduces to 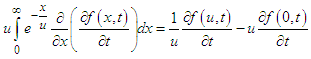 Therefore,
Therefore, 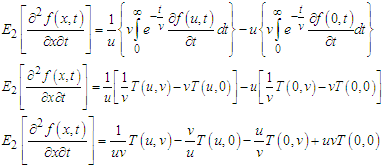
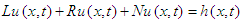
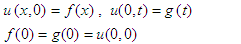
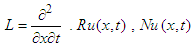 and
and 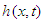 are linear term, non-linear differential term and source term respectively.Consequently, equation (4) becomes-
are linear term, non-linear differential term and source term respectively.Consequently, equation (4) becomes- 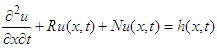 By double Elzaki transform the above equation is converted to-
By double Elzaki transform the above equation is converted to-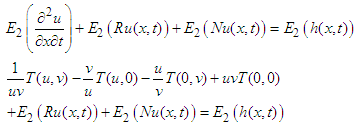
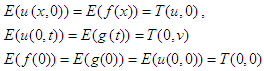
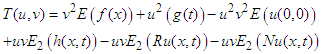 Now, on both sides of the above equation using inverse double Elzaki transform, finally-
Now, on both sides of the above equation using inverse double Elzaki transform, finally-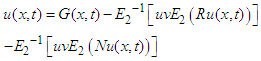
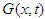 reflects the resulting source term.Consider an infinite series solution to solve non-linear mixed type PDEs by DEDM is
reflects the resulting source term.Consider an infinite series solution to solve non-linear mixed type PDEs by DEDM is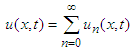
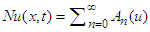
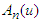 are Adomian polynomials with components
are Adomian polynomials with components 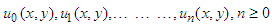 are defined by
are defined by 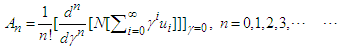
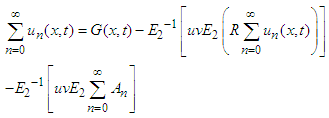
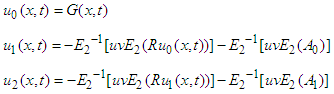 In general, the recursive relations are
In general, the recursive relations are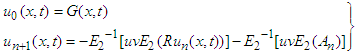 The values of all
The values of all 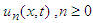 are obtained from the above recursive relation and substitute in equation (9), then the series solution for the given equation is found.
are obtained from the above recursive relation and substitute in equation (9), then the series solution for the given equation is found. 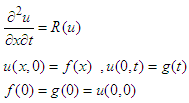 where,
where, 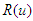 is a function of first degree.Example 1: Considering a Goursat problem which is linear and homogeneous-
is a function of first degree.Example 1: Considering a Goursat problem which is linear and homogeneous- 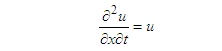
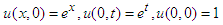
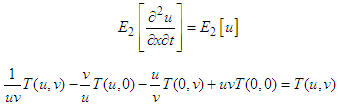
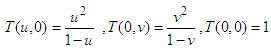 Using the above initial values, the equation (15) is reduced to-
Using the above initial values, the equation (15) is reduced to- 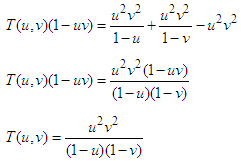 The exact solution is found by using inverse double Elzaki transform
The exact solution is found by using inverse double Elzaki transform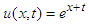 which is verified by the results obtained by VIM and ADM.
which is verified by the results obtained by VIM and ADM.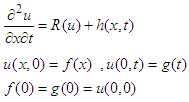 Where
Where 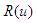 is a function of first degree.Example 2: Considering linear non-homogeneous Goursat problem-
is a function of first degree.Example 2: Considering linear non-homogeneous Goursat problem- 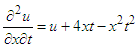
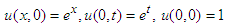
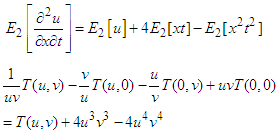
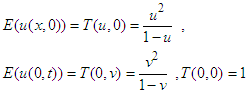 with the above conditions, the equation (18) is converted to
with the above conditions, the equation (18) is converted to 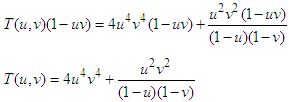 Applying inverse double Elzaki transform in the above equation
Applying inverse double Elzaki transform in the above equation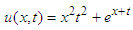 Which is the required exact solution. This result is completely similar with the result obtained by VIM and DTM.
Which is the required exact solution. This result is completely similar with the result obtained by VIM and DTM.
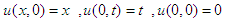
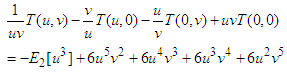 Applying single Elzaki transform in equation (20), conditions reduce to
Applying single Elzaki transform in equation (20), conditions reduce to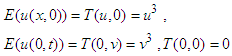 The transformed equation reduces with these conditions as
The transformed equation reduces with these conditions as 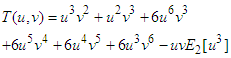 Again apply inverse double Elzaki transform in the above equation on both sides,
Again apply inverse double Elzaki transform in the above equation on both sides, 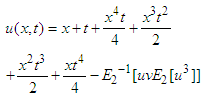
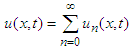
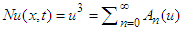
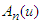 are Adomian polynomials of components
are Adomian polynomials of components 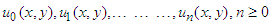 which is defined by the formula (11).Some Adomian polynomials of
which is defined by the formula (11).Some Adomian polynomials of 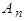 are found as
are found as 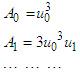 Then the equation (21) is transformed to
Then the equation (21) is transformed to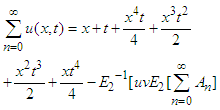 The following recursive relation is found by comparing the above equation on both sides,
The following recursive relation is found by comparing the above equation on both sides, 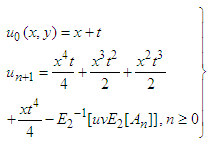 The following few components of un (x, y), n>0 are determined from the above relation
The following few components of un (x, y), n>0 are determined from the above relation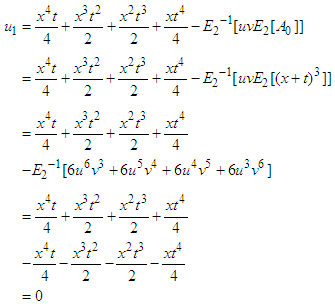 Consequently,
Consequently, 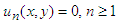 Substituting all values of un (x, y), n≥0 in equation (22), finally the series solution of the given equation is
Substituting all values of un (x, y), n≥0 in equation (22), finally the series solution of the given equation is  This results are in complete compliance with the result given by VIM and DTM.Example 4: Consider the non-linear homogeneous Goursat problem
This results are in complete compliance with the result given by VIM and DTM.Example 4: Consider the non-linear homogeneous Goursat problem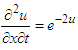
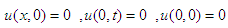
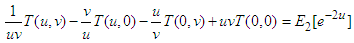 Using the single Elzaki transform the conditions in equation (25) reduces to
Using the single Elzaki transform the conditions in equation (25) reduces to 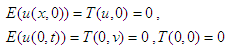 with these new conditions the above equation gives
with these new conditions the above equation gives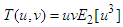 Operating inverse double Elzaki transform, find that
Operating inverse double Elzaki transform, find that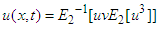
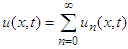
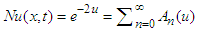
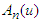 are Adomian polynomials of components
are Adomian polynomials of components 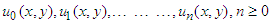 which is defined by the formula (11). Adomian polynomials
which is defined by the formula (11). Adomian polynomials 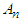 are
are 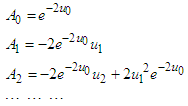 Then the equation (26) becomes
Then the equation (26) becomes 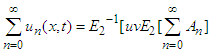 The recursive relationships are obtained by comparing both sides of the above equation
The recursive relationships are obtained by comparing both sides of the above equation 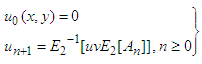 The following new components of
The following new components of 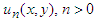 have been found from the above relationship.
have been found from the above relationship.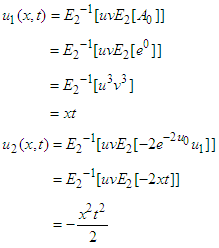 Like-wise
Like-wise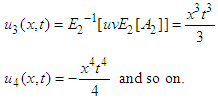 Putting all values of un (x, y), n≥0 in equation (27), finally the series solution of the given equation is
Putting all values of un (x, y), n≥0 in equation (27), finally the series solution of the given equation is 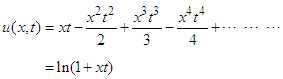 This finding is in complete compliance with the result obtained by VIM and DTM.
This finding is in complete compliance with the result obtained by VIM and DTM.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
