-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2021; 11(1): 1-4
doi:10.5923/j.am.20211101.01
Received: Jan. 21, 2021; Accepted: Feb. 21, 2021; Published: Feb. 28, 2021

An Application of Decision Theory for the Treatment of Bipolar Disorder
Alua Shakenova1, Roza Shakenova2
1Department of Mathematical and Computer Modelling, International Information Technologies University, Almaty, Kazakhstan
2Institute of Cybernetics and Information Technology, Kazakh National Research Technical University after K.I.Satbayev, Almaty, Kazakhstan
Correspondence to: Alua Shakenova, Department of Mathematical and Computer Modelling, International Information Technologies University, Almaty, Kazakhstan.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Bipolar disorder is a mental problem and causes difficulties in an individual’s life. Both mania and depressive states dissipate the energy required for normal functioning. Often untreated patients lose their families, jobs, and meaning of life, which is a dangerous situation. In severest cases, people may end up taking their own life. The authors constructed the transition probability matrix from empirical data of observations for a concrete patient. Furthermore, we calculated the limiting probabilities for states. After, we offered an efficient policy to treat bipolar disorder. The global factors which affect the individual’s happiness are health, career, and social contacts. Thus, the efficient policy needs to consider all these factors. The initial vector of potential energy was introduced. Here, the reward was the energy gained. Consequently, the final rewards were calculated. The main goal is to maximize potential energy for a normal state by decreasing the limiting probabilities of being in manic and depressive states. Boltzmann established that probability and energy are mutually related. These quantities are directly proportional. Boltzmann's idea was followed in this article, so the initial vector is given as the initial energy vector. The final result is potential energy. The recommendations for further research are given.
Keywords: Bipolar Disorder, Transition probabilities, Policy, Reward
Cite this paper: Alua Shakenova, Roza Shakenova, An Application of Decision Theory for the Treatment of Bipolar Disorder, Applied Mathematics, Vol. 11 No. 1, 2021, pp. 1-4. doi: 10.5923/j.am.20211101.01.
Article Outline
1. Introduction
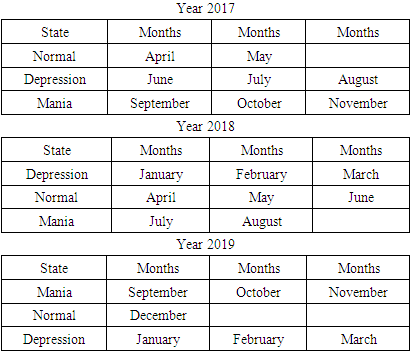
- Around 45 million of the population suffered from Bipolar disorder in 2017 [1]. This mental disease is characterized by instant mood changes. Mostly, there are two stages manic and depressive. Mania occurs shorter time and has the following symptoms: the deprivation of sleep, optimistic mood (euphoria), verbosity, and the abundance of incredible ideas. Depression takes a longer time and may last for years; bad mood, oversleeping, decreased mental and physical activity, hopeless thoughts, and loss of interest in life. The switches are happening at a random time thus cannot be controlled. Most of the patients diagnosed with depression lost the meaning of life. The life seemed worthless; the connections between them and their close ones vanished within a time of disease. The majority felt rejected, isolated from society, thus felt lonely, concentrated on failures, and could not find happy moments. At those times, they demonstrated the weak will to change a life. The patients diagnosed with bipolar disorder are at risk of committing suicide [2]. Hence, the idea of this paper is to construct the transition probabilities matrix from a dataset, interpret the results, and give further recommendations for treatment.
2. Literature Review
- Alafchi et al. [3] used the maximum likelihood method to obtain a probability transitional matrix for two states: mania and depression. Staying in state 1 was 0.76, and remaining in state 2 was 0.93. He concluded that the patient tends to stay in one of the persistent states (not transitional). Prisciandaro et al. [4] identified three mood states: euthymic (stable), depressed and mixed. The mixed state showed the similar symptoms as the manic state. For three states the transitional probabilities were found to be 0.94, 0.72 and 0.37 accordingly. However, they both did not calculate the final state probabilities, which are essential for treatment. Therefore, our research paper considers three states: mania, depression, and normal state. Moreover, we have calculated the limiting probabilities of these states (they were 1/3 each). This means that the patient has an equal chance, if untreated, to stay at any of these states. Zimmerman et al. [5] stated that the patients get the correct diagnosis only after 10 years. This delays the receipt of adequate treatment, increasing the costs of treatment. He recommends inquiring more about the history of mania to detect Bipolar disorder carefully. In this study, the mania and depression history were assessed carefully for the patient.
3. A Physical Interpretation of Bipolar Disorder
- No uniform allocation of energy is seen in bipolar patients. The lowest energy level is in the depression episode and the highest in mania (or hypomania). The target is to distribute the energy uniformly in the two episodes. Minimize it in the mania and maximize in the depression
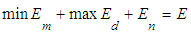 | (1) |
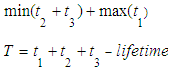 | (2) |
 | Figure 1. The global factors defining happiness |
|
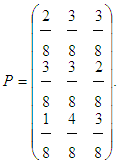 | (3) |
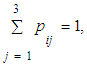 | (4) |
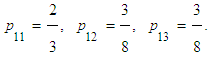 Therefore our objective is to increase the values
Therefore our objective is to increase the values 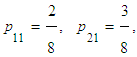
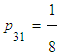 [6], [7], [8] for this purpose let’s introduce the initial vector. It is the energy, which should be allocated efficiently by the individual (potential energy). Decreasing entropy shows that the person is curing. The different policies are offered for a patient
[6], [7], [8] for this purpose let’s introduce the initial vector. It is the energy, which should be allocated efficiently by the individual (potential energy). Decreasing entropy shows that the person is curing. The different policies are offered for a patient 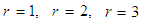 [9], [10], [11]. For first policy , clinical psychologist offers the therapy that improves health by sticking to a diet and exercising.For the second
[9], [10], [11]. For first policy , clinical psychologist offers the therapy that improves health by sticking to a diet and exercising.For the second 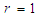 the patient is advised to switch the job or change the specialty. For third, the doctor offers to change the surrounding environment, update the social contacts. Initial vector of energy:
the patient is advised to switch the job or change the specialty. For third, the doctor offers to change the surrounding environment, update the social contacts. Initial vector of energy: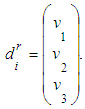 | (5) |
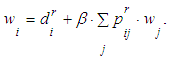 | (6) |
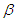 is the discount factor,
is the discount factor, 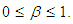 Let the first policy to have the initial vector of energy
Let the first policy to have the initial vector of energy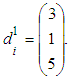 | (7) |
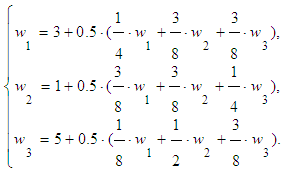 | (8) |
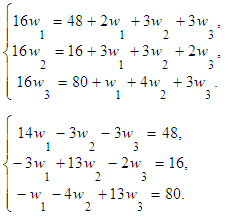 Obtain the final results:
Obtain the final results: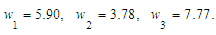 Explaining the initial reward vector,
Explaining the initial reward vector,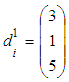 | (9) |
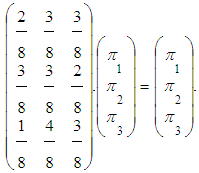 | (10) |
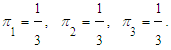 This paper deals with a case with one patient. Based on the observations, a transitional matrix of probability was obtained. This matrix shows the patient's states change from normal to depressive, from depressive to manic, and vice versa. A clinical psychologist should select the individual treatment for a patient. We selected the patient who gave conscious consent for examination. The limitation of the study: genetic predisposition to bipolar disorder was not assessed.At the physical level, a person's state can be interpreted as potential energy. The energy vector is introduced as the initial energy vector.
This paper deals with a case with one patient. Based on the observations, a transitional matrix of probability was obtained. This matrix shows the patient's states change from normal to depressive, from depressive to manic, and vice versa. A clinical psychologist should select the individual treatment for a patient. We selected the patient who gave conscious consent for examination. The limitation of the study: genetic predisposition to bipolar disorder was not assessed.At the physical level, a person's state can be interpreted as potential energy. The energy vector is introduced as the initial energy vector.4. Conclusions
- For the second and third policies analogically, the corresponding values can be obtained [12]. We calculate the limiting probabilities. A policy with a limiting probability for a normal state greater than the limiting probability for depressive and manic states is selected as the best. At the same time, the number of policies may increase. Different combinations of strategies can be generated. Each strategy includes a chain of policies. Consequently, select the optimal strategy among the proposed. The result is the highest potential energy for the normal state by reducing the transitional probabilities for depressive and manic states. This article launches a series of papers on mathematical applications to bipolar disorder treatment. Bipolar disorder is a particular issue in developing countries because dictatorship suppresses the human rights of individuals. Therefore, the main focus of this article is not the theory of pure mathematics but the applications of applied mathematics. We propose the basic ideas of a patient's correct treatment direction. The problem turns out to be the wrong distribution of the patient's energy. In subsequent articles, this problem will find its further development. The optimal energy distribution for the treatment of bipolar disorder has been studied hardly. Even though we sought all relevant articles, we could not find a similar approach. Therefore, we achieved a novelty.
ACKNOWLEDGEMENTS
- Funding: This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML