-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2020; 10(2): 28-33
doi:10.5923/j.am.20201002.02
Received: Sep. 16, 2020; Accepted: Oct. 12, 2020; Published: Oct. 26, 2020

Solving Fourth Order Boundary Value Problem by Using Extended Quantic B-spline Interpolation
Intidhar Zamil Mushtt, Saad Shakir Mahmood, Dunya Mohamed Hamed
Mustansiriyah University, College of Education, Baghdad, Iraq
Correspondence to: Intidhar Zamil Mushtt, Mustansiriyah University, College of Education, Baghdad, Iraq.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The aim of this paper is to solve the fourth order boundary value problem by using quantic b-spline where the rectangular system be solved by using singular value decomposition technique (SVD), and because the solution is not unique we used the least square optimization to optimal the numerical solution of the BVP. Numerical results are reported where we make a comparison between the exact solution and the approximate solution using the new technique.
Keywords: Quantic b-spline, Fourth order BVP, Approximate solution, Exact solution, SVD
Cite this paper: Intidhar Zamil Mushtt, Saad Shakir Mahmood, Dunya Mohamed Hamed, Solving Fourth Order Boundary Value Problem by Using Extended Quantic B-spline Interpolation, Applied Mathematics, Vol. 10 No. 2, 2020, pp. 28-33. doi: 10.5923/j.am.20201002.02.
1. Introduction
- Differential equations are an important tool in constructing mathematical models for physical phenomena. This modeling allows for a much clearer understanding and interpretation of the particular event. Finding the analytical and approximate solution of these models with boundary conditions thus becomes essential. Many analytical and approximate methods were developed solution of ordinary differential equation with boundary value conditions and a many these method as [1,2,3,4].In this paper, the approximate solution of fourth order boundary value problem will be determine via Quantic B-spline, and comparisons with current studie will be made in the literature where the extended are given by the continuous least square optimization.Since the fourth order B.V.P which is in the from:
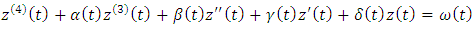 | (1) |
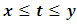 , and
, and 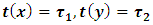 Where
Where 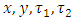 are all constants, and
are all constants, and  are all a continuous functions defined on interval
are all a continuous functions defined on interval 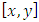 .Hence there has been much research activity concerning B-spline for solving boundary value problem we refer the reader [5,6,7,8,9,10].Quantic B-spline interpolation method [11]The interval
.Hence there has been much research activity concerning B-spline for solving boundary value problem we refer the reader [5,6,7,8,9,10].Quantic B-spline interpolation method [11]The interval 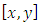 of domain has been subdivided as
of domain has been subdivided as 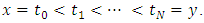 To provide the support for the quantic B-spline near the end boundaries, ten additional knots have been introduced as
To provide the support for the quantic B-spline near the end boundaries, ten additional knots have been introduced as 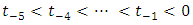 and
and 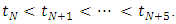 The basis function
The basis function 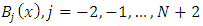 of quantic B-spline are as:
of quantic B-spline are as: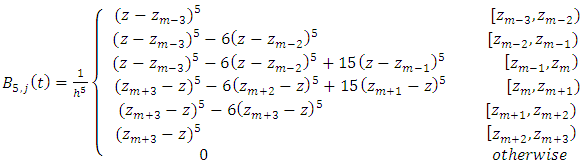 | (2) |
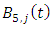 form a basis over the region
form a basis over the region 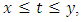 the global approximation defined using quantic B-spline:
the global approximation defined using quantic B-spline: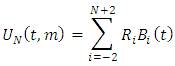 | (3) |
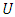 and it's derivatives of
and it's derivatives of 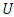 to fourth order are given in terms of the parameters
to fourth order are given in terms of the parameters 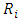 from the use of spline (2) and the trial solution (3).
from the use of spline (2) and the trial solution (3).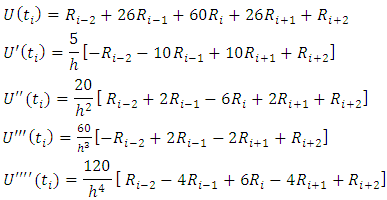 Definition: [13]Any real number
Definition: [13]Any real number  matrix
matrix 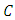 can be decomposed as
can be decomposed as 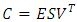 where
where 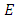 is
is 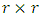 and column orthogonal (it's column are eigenvectors of
and column orthogonal (it's column are eigenvectors of 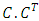 )
) 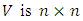 and orthogonal (it's column are eigenvectors of
and orthogonal (it's column are eigenvectors of 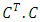 )
) 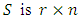 diagonal (non-negative real values called singular values)
diagonal (non-negative real values called singular values)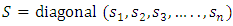 order so that
order so that 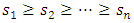 (if
(if 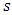 is a singular value of
is a singular value of 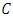 it's square is an eigenvalue of
it's square is an eigenvalue of 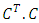 ).Extended Quantic B-spline by using SVD and continuous least square errorConsider the Fourth order BVP:
).Extended Quantic B-spline by using SVD and continuous least square errorConsider the Fourth order BVP: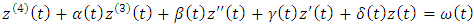 On
On 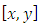 such that
such that 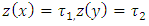 , where
, where 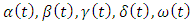 are a continuous function defined on
are a continuous function defined on 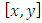 , and
, and 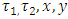 are all constants.The quantic B-spline is defined in equation (2)Then
are all constants.The quantic B-spline is defined in equation (2)Then 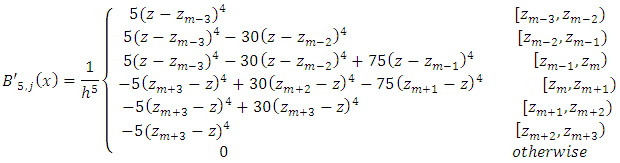 And
And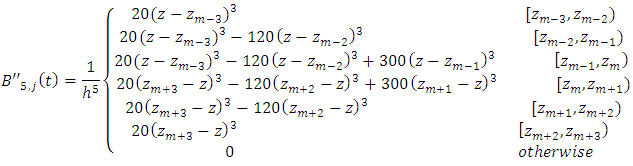
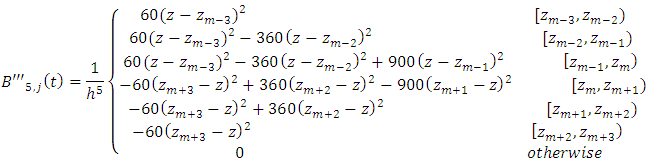
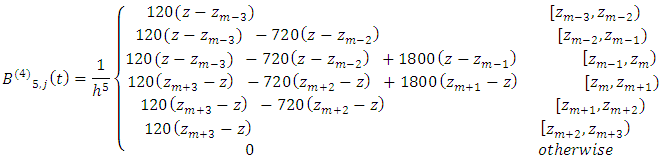 Let
Let 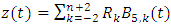 , be an approximate solution of equation (1) where
, be an approximate solution of equation (1) where 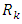 is unknown real coefficients, let
is unknown real coefficients, let 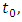
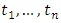 are
are 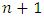 grid points in the interval
grid points in the interval 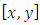 and also
and also 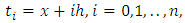
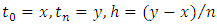 in order to get a matrix of transactions that is contrary to the matrix of transaction that is contrary to the matrix from behind to make the image on the following form:
in order to get a matrix of transactions that is contrary to the matrix of transaction that is contrary to the matrix from behind to make the image on the following form: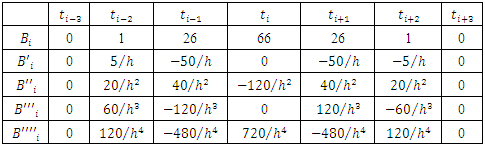 This system can be written in matrix form as follows
This system can be written in matrix form as follows 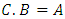 such that
such that  Where
Where 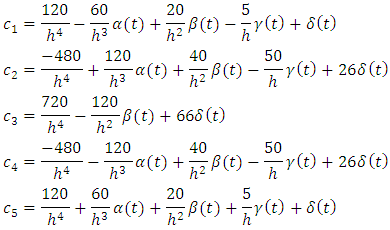 And
And 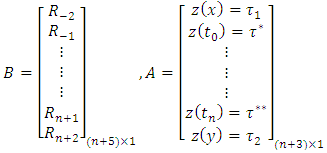 The singular decomposition of
The singular decomposition of 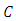 has the form
has the form 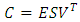 so
so 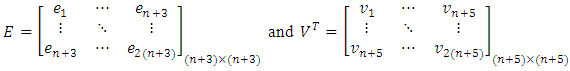 and
and 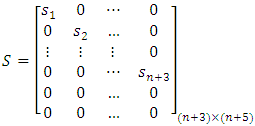 So
So 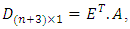 let
let 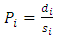 then
then 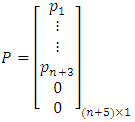 and
and 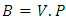 Hence
Hence 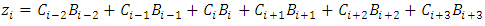
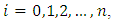 then we have
then we have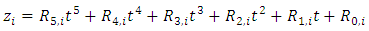 be the solution of ODE by Quintic B-spline on the interval
be the solution of ODE by Quintic B-spline on the interval 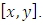 The last equation can be solved by using continuous least square error to obtain the values of the constants with make the difference between the left-hand side and the right –hand side of BVP (1) is minimum.Example 1: Consider the following ODE
The last equation can be solved by using continuous least square error to obtain the values of the constants with make the difference between the left-hand side and the right –hand side of BVP (1) is minimum.Example 1: Consider the following ODE 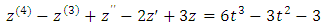 With boundary conditions
With boundary conditions 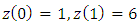 and the exact solution is
and the exact solution is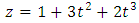 Now let
Now let  then
then 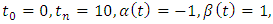
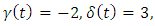
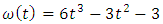 This system can be written as follows:-
This system can be written as follows:-  Such that
Such that 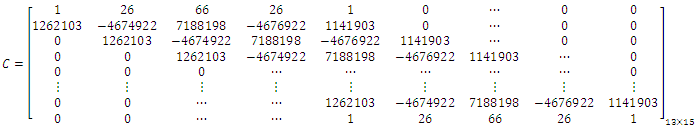 And
And 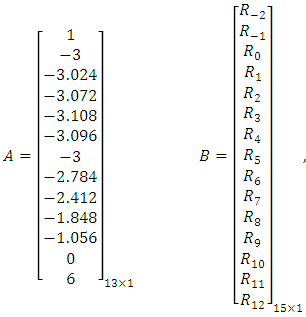 Since
Since 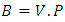 be the values of the coefficient
be the values of the coefficient 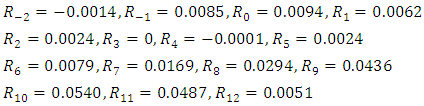
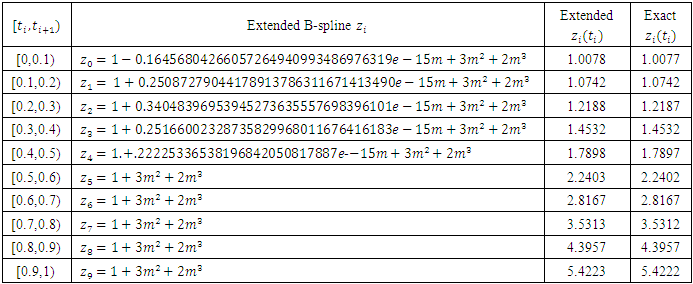
|
2. Conclusions
- Fourth order boundary value problem solved by using the extended quantic B-spline with continuous Least Square approximation and singular value decomposition technique. The numerical results showed that the extended quantic B-spline approximations are considered very well.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML