-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2020; 10(1): 12-19
doi:10.5923/j.am.20201001.03
Received: July 21, 2020; Accepted: August 5, 2020; Published: August 29, 2020

Joint Influence of Double Sampling and Randomized Response Technique on Estimation Method of Mean
Nadia Mushtaq1, Muhammad Noor-ul-Amin2
1Department of Statistics, Forman Christian College University, Lahore
2COMSATS Institute of Information and Technology Lahore, Pakistan
Correspondence to: Nadia Mushtaq, Department of Statistics, Forman Christian College University, Lahore.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this article, the problem of estimation under two-phase random sampling using randomized response technique is considered. In two-phase (double) sampling, the expression of bias and mean square error (MSE) up to the first-order approximations are derived for the proposed estimators. Simulation studies and real data are presented to demonstrate the performance of proposed estimators.
Keywords: Double Sampling, Sensitive Variable, Randomized Response Technique
Cite this paper: Nadia Mushtaq, Muhammad Noor-ul-Amin, Joint Influence of Double Sampling and Randomized Response Technique on Estimation Method of Mean, Applied Mathematics, Vol. 10 No. 1, 2020, pp. 12-19. doi: 10.5923/j.am.20201001.03.
Article Outline
1. Introduction
- It is common practice in sample survey we obtain the information about auxiliary variable(s) from a larger sample at first phase and relatively small sample from the second phase by using two-phase sampling procedure. Many authors worked on two-phase random sampling such as: Sukhatme (1962), Singh and Vishwakarma (2007), Sahoo et al. (2010) Noor-ul-amin and Hanif (2012), Sanaullah et al. (2014), etc.In survey sampling information on sensitive variable would be collected by using randomized response technique introduced by Warner (1965), because direct reliable information on variable of interest is sometime may not possible. Several authors have worked on randomized response techniques on estimation of mean, including Eichhorn and Hayre (1983), Gupta et al. (2002), Chang et al. (2005), Huang (2008). Sousa et al. (2010) introduced ratio estimators by using non-sensitive auxiliary information. Gupta et al. (2014) presented ratio and regression estimator using optional scrambling. Mushtaq et al. (2017) presented a family of estimators of a sensitive variable using auxiliary information in stratified random sampling. Noor-ul-amin et al. (2018) proposed estimation of mean using generalized optional scrambled responses in the presence of non-sensitive auxiliary variable. Saleem I. et al (2019) presented estimation of mean of a sensitive quantitative variable in complex survey: improved estimator and scrambled randomized response model. Partha Parichha et al. (2020) discuss the development of estimation procedure of population mean in Two-Phase Stratified Sampling.Encourage the above work, we have suggested a generalized class of estimators in two-phase sampling using randomized response technique. The main purpose is to suggest a strategy of two-phase (double) sampling in randomized response technique and proposed general family of estimators for estimating the finite population mean of a sensitive variable with non-sensitive auxiliary variable based on RRT in two- phase (double) random sampling.
2. Sampling Strategy
2.1. Notations & Scheme of Selection of Sample
- We consider the finite population
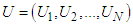 in which
in which 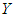 be the sensitive study variable,
be the sensitive study variable, 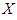 be non-sensitive auxiliary variable which is correlated with
be non-sensitive auxiliary variable which is correlated with 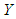 and
and 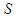 be scrambling variable independent of
be scrambling variable independent of 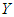 and
and 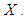 The reported response of the respondents is
The reported response of the respondents is 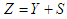 , and
, and 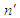 is the number of units in the first sample whereas n is the number of units in the second sample. Only in the second sample both study and auxiliary variables are observed, in the first sample only auxiliary variable is observed because study variable is expensive.The two-phase sampling strategy is given below:1. The first phase, a large sample of a fixed size
is the number of units in the first sample whereas n is the number of units in the second sample. Only in the second sample both study and auxiliary variables are observed, in the first sample only auxiliary variable is observed because study variable is expensive.The two-phase sampling strategy is given below:1. The first phase, a large sample of a fixed size 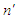 is drawn from N to observe only
is drawn from N to observe only 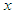 or auxiliary variable.2. The second phase sample, a sub-sample of fixed size
or auxiliary variable.2. The second phase sample, a sub-sample of fixed size 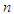 is drawn from
is drawn from 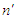 to observe
to observe 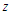 and
and 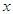 , so that
, so that 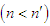 .Let define the following notations:
.Let define the following notations: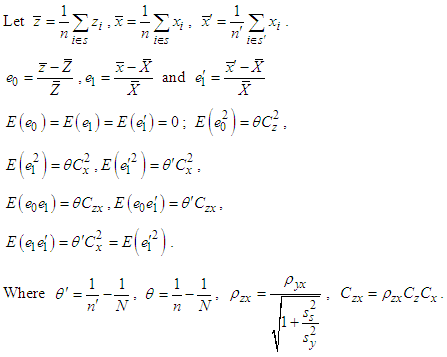
2.2. Discussion on Estimators in Double Sampling Strategy in RRT
- Firstly, we introduce some existing estimators in double sampling using RRT.The mean and variance of the usual mean estimator in RRT is given by
 | (2.1) |
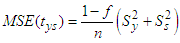 | (2.2) |
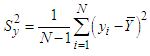 and
and 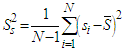 .A ratio estimator in two-phase sampling in RRT is given as:
.A ratio estimator in two-phase sampling in RRT is given as: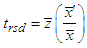 | (2.3) |
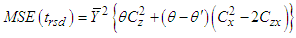 | (2.4) |
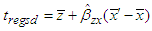 | (2.5) |
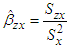
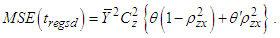 | (2.6) |
3. Proposed Estimators
- We propose the following a class of generalized estimators in two-phase sampling:
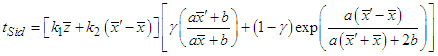 | (3.1) |
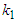 and
and 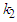 are weights whose values are to be determined,
are weights whose values are to be determined, 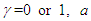 and
and 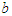 are the parameters of the auxiliary variables.From
are the parameters of the auxiliary variables.From 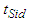 for
for 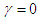 , we obtain the following estimators
, we obtain the following estimators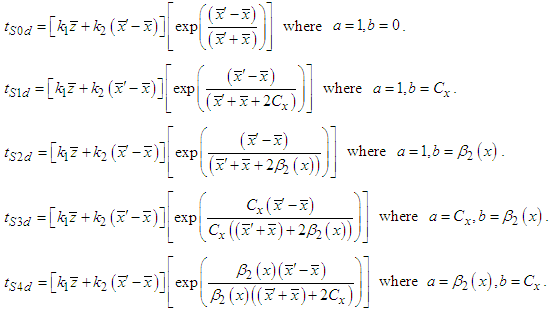 From
From 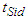 for
for 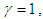 we obtain the following estimators
we obtain the following estimators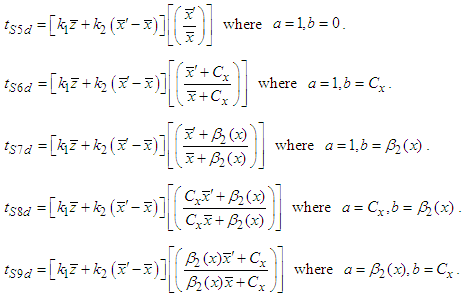 Expanding (3.1), we have
Expanding (3.1), we have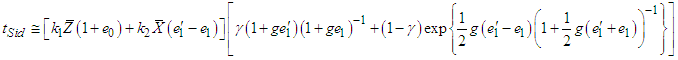 | (3.2) |
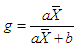
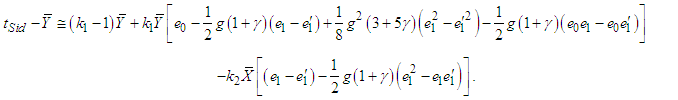 | (3.3) |
 and
and  of
of  are given by
are given by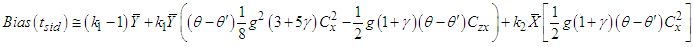 | (3.4) |
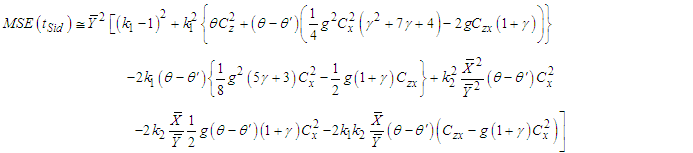 | (3.5) |
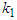 and
and 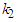 , respectively, are found as,
, respectively, are found as,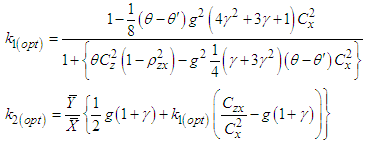 Substituting these optimum values in (3.5), the minimum
Substituting these optimum values in (3.5), the minimum 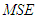 of
of 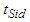 is given by
is given by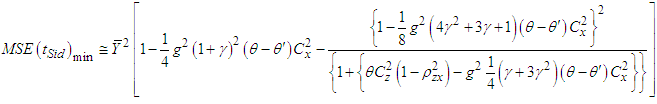 | (3.6) |
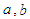 and
and 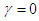 or
or 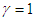 , we can get the minimum
, we can get the minimum 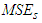 of
of 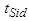
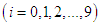 .
.4. Simulation Study & Efficiency Comparison of Proposed Estimators
- We use the simulation studies for efficiency comparison by empirically and theoretically. Two populations for simulation studies of size 1000 each from bivariate normal populations for (Y, X), with different covariance matrices are used. The Scrambling variable
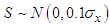 and
and 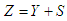 . Population 1 Mean of
. Population 1 Mean of 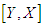 given as
given as 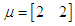
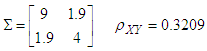 Population 2 Mean of
Population 2 Mean of 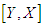 given as
given as 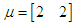
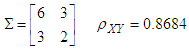 For all populations, we consider four sample sizes:
For all populations, we consider four sample sizes: 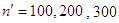 and
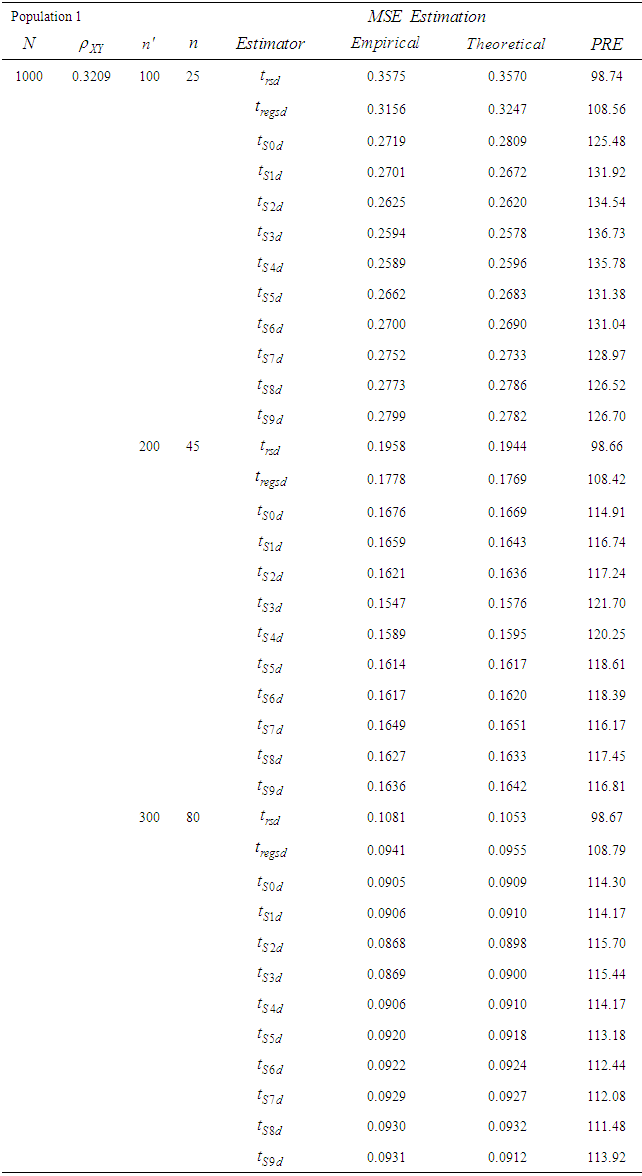
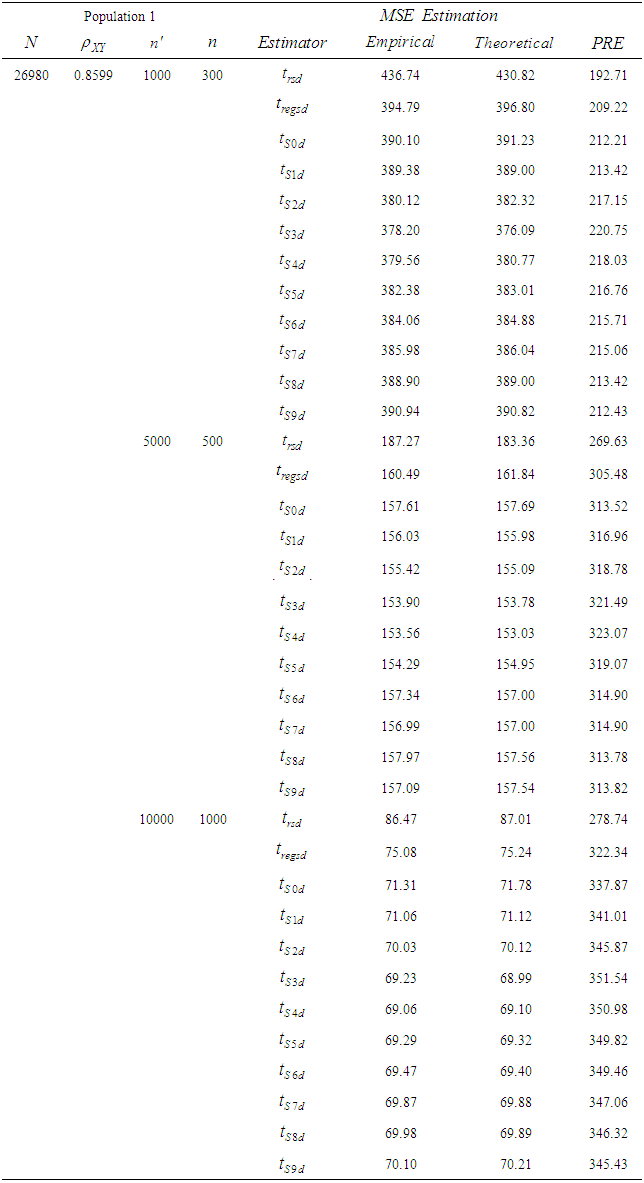
and 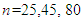 respectively. The empirical and theoretical MSE’s for various sensitive mean estimators are given in Tables 1-2. We estimate the empirical MSE using 10000 samples of different sizes selected from each population.
respectively. The empirical and theoretical MSE’s for various sensitive mean estimators are given in Tables 1-2. We estimate the empirical MSE using 10000 samples of different sizes selected from each population. 5. Real Data Set Application of Two-Phase or Double Sampling in RRT
- For this analysis, we consider the real population used in Gupta et al. (2012). Let
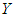 be the monthly salaries amount in 2010,
be the monthly salaries amount in 2010, 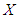 is the number of employees available from business data register and
is the number of employees available from business data register and 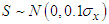 . For this population, we have:
. For this population, we have: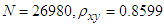 ,
, 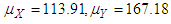 (in thousands of)
(in thousands of) 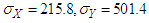 and
and 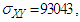
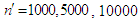 and
and 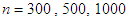 respectively.Numerical results of empirical and theoretical MSE based on population data is given in Table 3.The following expression is used to obtain percent relative efficiency (PRE) of different estimators with respect to
respectively.Numerical results of empirical and theoretical MSE based on population data is given in Table 3.The following expression is used to obtain percent relative efficiency (PRE) of different estimators with respect to 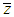 :
: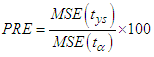 Where
Where 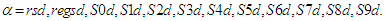 In Table 3 we present the empirical and theoretical results of MSE estimates and PRE of the various estimators in the stratified sample.
In Table 3 we present the empirical and theoretical results of MSE estimates and PRE of the various estimators in the stratified sample. 6. Conclusions
- In this study, we suggested the idea of two-phase sampling in randomized response technique. We consider a general class of estimators for mean of sensitive variable based on randomized response technique in two-phase sampling. In Tables 1-3, we present the results of the theoretical and empirical MSE and PRE of the estimators in two-phase sampling using randomized response technique. These results are computed with a simulation studies and using a real data set.
Appendix
|
|
|
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML