-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2020; 10(1): 7-11
doi:10.5923/j.am.20201001.02
Received: July 4, 2020; Accepted: August 5, 2020; Published: August 26, 2020

Mathematical Analysis of the Operating Characteristics of a Barbering Shop in Kumasi Using Queuing Theory
Douglas Kwasi Boah
Department of Mathematics, C. K. Tedam University of Technology and Applied Sciences, Navrongo, Ghana
Correspondence to: Douglas Kwasi Boah, Department of Mathematics, C. K. Tedam University of Technology and Applied Sciences, Navrongo, Ghana.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Most barbering shops in Ghana do not receive optimal patronage as a result of unscientific ways of operation and this problem affects the shops immensely. In this paper, the concept of queuing theory has been applied to analyze the operating characteristics of a barbering shop in Kumasi, Ghana and come out with suggestions as to how the shop should optimize its operations so as to receive higher patronage. Multi-Server Queuing Model with Poisson Arrivals and Exponential Service Times was adopted for the study. Close observation was used to collect primary data for the study. Based on the collected data, Management Scientist Version 5 Software was used to perform the analysis. Specifically, the probability of no customers in the shop, the average number of customers in the shop, the average number of customers in a waiting line, the average time a customer spends in the shop, the average time a customer spends in a waiting line and the probability that an arriving customer must wait for service have been obtained for the manager of the shop. Finally, the study has proposed some recommendations for optimal operation of the shop.
Keywords: Queuing Theory, Waiting Lines, Service Facility, Multi-Server Queuing Model, Customers, Optimal Operation
Cite this paper: Douglas Kwasi Boah, Mathematical Analysis of the Operating Characteristics of a Barbering Shop in Kumasi Using Queuing Theory, Applied Mathematics, Vol. 10 No. 1, 2020, pp. 7-11. doi: 10.5923/j.am.20201001.02.
Article Outline
1. Introduction
- Waiting for service is part of everyday life. We wait for service in banks, restaurants, airports, post offices, supermarkets, toll booths, hospitals, cafeteria, ticket booths, bus stops, workshops, fuel stations, fitting shops and so on. The waiting phenomenon is not an experience limited to human beings. Jobs wait to be processed on a machine, planes circle in stack before given permission to land, and cars stop at traffic lights. Eliminating waiting completely is not a feasible option because the cost of installing and operating a service facility can be prohibitive. Our only recourse is to strike a balance between cost of offering a service and the cost of waiting experienced by customers. Queuing theory is the vehicle for achieving this. Sundarapandian [1] defined queuing theory as the mathematical study of waiting lines, or queues. Queuing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. According to Taha [2], the principal players in a queuing situation are the customer and the server. The one who demands the service is the customer whereas the one, who provides the service, is the server. The customers arrive at a service facility from a source which may be finite or infinite. A finite source limits the number of arriving customers whereas an infinite source is, for all practical purposes, forever abundant. Queue discipline which represents the order by which customers are served or attended to plays a significant role in queuing theory. According to Laguna [3], first in first out also called first-come, first-served (FCFS) is a principle that states that customers are served one at a time and that the customer that has been waiting the longest is served first. According to Penttinen [4], last in first out principle serves customers one at a time, but the customer with the shortest waiting time will be served first. It is also known as a stack. Also, for processor sharing principle, service capacity is shared equally among customers. Moreover, for priority principle, customers with high priority are served first. Priority queues can be of two types, non-pre-emptive (where a job in service cannot be interrupted) and pre-emptive (where a job in service can be interrupted by a higher-priority job). According to Sharma [5], a patient customer waits in the queue until served and does not switch between waiting lines. A balking customer does not join the queue either by seeing the number of customers already in a service facility or by estimating the excessive waiting time for the desired service. A reneging customer, after joining the queue, waits for some time but leaves before being served on account of certain reasons. A jockeying customer moves from one queue to another hoping to receive service more quickly. Variations in the elements of a queuing situation gave rise to a variety of mathematical queuing models.Most barbering shops in Ghana do not receive optimal patronage as a result of unscientific ways of operation and this problem affects the shops immensely. In this paper, the concept of queuing theory has been used to analyze the operating characteristics of a barbering shop in Kumasi, Ghana and come out with suggestions as to how the shop should optimize its operations so as to receive higher patronage. Waiting for service at the barbering shop studied can be very stressful and this causes a number of customers to renege or balk. This problem among others necessitated the choice of that particular barbering shop for the study. The barbering shop requires anonymity and so its name has been withheld throughout the paper.
2. Literature Review
- According to Sundarapandian [1], queuing theory has its origins in research by Agner Krarup Erlang when he created models to describe the Copenhagen telephone exchange. The ideas have since received much attention. A number of papers in the theory and applications of queuing theory have been reported in the literature. Schrage [6] presented analysis and optimization of a queuing model of a real-time computer control system. Fomundam and Herrmann [7] carried out a survey of queuing theory applications in healthcare. Shanthikumar et al [8] applied queuing theory to semiconductor manufacturing systems. Mishra and Yadav [9] presented a computational approach to cost and profit analysis of clocked queuing networks. Mishra and Yadav [10] used computing algorithms to calculate the total expected cost, the total expected revenue and the total optimal profit in a finite capacity optimization model of a loss-queuing system. Ghimire and Basnet [11] presented a finite capacity queuing system with vacation and service breakdown. Goswami and Laxmi [12] presented performance analysis of a renewal input bulk service queue with accessible and non-accessible batches. Kamoun [13] presented performance analysis of two priority queuing systems in Tandem. Tabari et al [14] applied queuing theory to human resource management. Ammar [15] carried out transient analysis of two-heterogeneous servers queue with impatient behaviour. Ayyappan et al [16] performed transient analysis of single server queuing system with batch service under catastrophe. Brahma [17] presented queuing theory and customer satisfaction: a review of terminologies, trends and applications to hospital practice. Jiang et al [18] developed a three-velocity queuing model for congested traffic flow simulation. Kumar et al [19] modelled insurance business facing customer impatience using queuing theory. Lade et al [20] used queuing theory to simulate the total waiting time, average queue length, average waiting time etc. of patients in hospitals. Chakravarthy [21] presented a multi-server queuing model with server consultations. Gong and Li [22] developed a queuing time decision model taking into consideration call center customer abandonment behaviour. Sani and Daman [23] presented mathematical modelling in heavy traffic queuing systems. Singla and Garg [24] presented transient and numerical solution of a feedback queuing system with correlated departures. Zeng et al [25] developed a transient queuing model for analyzing and optimizing gate congestion of railway container terminals. Vahdani and Mohammadi [26] presented a bi-objective interval-stochastic robust optimization model for designing closed loop supply chain network with multi-priority queuing system. Vass and Szabo [27] applied queuing theory to patient flow in an emergency department. Sadjadi et al [28] applied a queuing approach to a stochastic location-inventory problem with two different mean inventory considerations. Babadi et al [29] designed a reliable multi-objective queuing model of a petrochemical supply chain network under uncertainty. Cho et al [30] used queuing theory to analyse changes in outpatients’ waiting times in hospitals before and after the introduction of Electronic Medical Record (EMR). Gumus et al [31] applied queuing theory to a fast food outfit. Wang [32] applied queuing theory to characterize and optimize passenger flow at airport security checkpoints. Adeke [33] applied queuing theory to airport check-in systems using Manchester and Leeds-Bradford Airports for the study. Zhang et al [34] presented user-based discrete-time queuing analysis for opportunistic spectrum access in cognitive radio networks.From the reviewed literature and to the best of my knowledge, application of queuing theory to a barbering shop appears non-existent thereby necessitating this study so to fill the knowledge gap.
3. Materials and Methods
- According to Sharma [5], different models in queuing theory are classified by using special (or standard) notations described initially by Kendall [35] in the form (a/b/c). Later, Lee [36] added the symbols d and e to the Kendall notation. Now, in the literature of queuing theory, the standard format used to describe the main characteristics of parallel queues is given as {(a/b/c): (d/e)}, where a = arrivals distribution, b = service time (or departures) distribution, c = number of service channels (servers), d = maximum number of customers allowed in the system (in queue plus in service) and e = queue (or service) discipline.The following descriptive notations are used for the arrival and service time distribution (i.e. to replace notations a and b): M = Markovian (or Exponential) inter-arrival time or service-time distribution; D = Deterministic (or constant) inter-arrival time or service time; G = General distribution of service time (departures), i.e. no assumption is made about the type of distribution with mean and variance; GI = General probability distribution-normal, uniform or any empirical distribution, for inter-arrival time and Ek = Erlang-k distribution for inter-arrival or service time with parameter k (i.e. if k =1, Erlang is equivalent to exponential and if k = ∞, Erlang is equivalent to deterministic). For example, a queuing system in which the number of arrivals is described by a Poisson probability distribution, the service time is described by an exponential distribution, and there is a single server, would be represented by M/M/1. For a detailed discussion of the concept of queuing theory, the interested reader is referred to Taha [2], Sharma [5] and Hillier and Lieberman [37]. Multi-Server Queuing Model with Poisson Arrivals and Exponential Service Times was adopted for the study. Here, there are multiple but identical servers in parallel, for handling arriving customers. For this queuing model, it is assumed that arrivals follow a Poisson probability distribution at an average rate of λ customers per unit of time. It is also assumed that they are served on a first-come, first-served basis by any of the servers. The service times are distributed exponentially, with an average of μ customers per unit of time. It is further assumed that only one queue is formed. If k is the number of service channels or servers, the following are some of the equations usually used in multiple-server queuing model for which the overall average service rate, kµ, is greater than the average arrival rate, λ.The probability that all k service channels are idle (i.e., the probability of zero customers in the system) is given by:
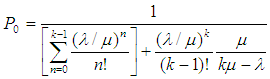 | (1) |
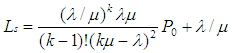 | (2) |
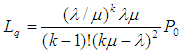 | (3) |
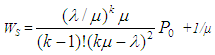 | (4) |
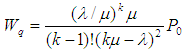 | (5) |
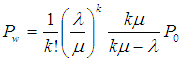 | (6) |
4. Results and Discussions
- The barbering shop considered in the study has four (4) equally competent barbers. Close observation was used to collect primary data for the study as shown in Table 1.
|
5. Conclusions
- The concept of queuing theory has been successfully used to analyze the operating characteristics of a barbering shop in Kumasi, Ghana. Specifically, the probability of no customers in the shop, the average number of customers in the shop, the average number of customers in a waiting line, the average time a customer spends in the shop, the average time a customer spends in a waiting line and the probability that an arriving customer must wait for service have been obtained for the manager of the shop. It is recommended that, for optimal operation of the barbering shop in order to receive higher patronage, the manager should• Urgently employ at least two additional barbers. • Create an inviting environment. To do this, all customers should receive a warm greeting as soon as they enter the shop. Also, the barbers should be trained to have a decent sense of humor so as to entertain the customers. • Invest in subscriptions to the most popular news and sports television channels.• Ensure that the barbering shop is always clean and comfortable.• Always offer consistent service. To ensure this, the shop should always be opened on time and sometimes stay opened a little while longer.• Build a healthy relationship with the customers. The study has contributed significantly to knowledge by providing scientific and optimal ways by which every barbering shop can operate so as to receive higher patronage. Also, the study has filled the knowledge gap of application of queuing theory to a barbering shop which appeared non-existent.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML