-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2020; 10(1): 1-6
doi:10.5923/j.am.20201001.01

A Technique of Discretizing Continuous Data for Programming Adaptive Deterministic Cubature Methods in Moderate Dimensions
Dinh Van Tiep, Tran Thi Hue
Faculty of International Training, Thai Nguyen University of Technology, TNU, Thai Nguyen, Vietnam
Correspondence to: Dinh Van Tiep, Faculty of International Training, Thai Nguyen University of Technology, TNU, Thai Nguyen, Vietnam.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Cubature methods has been used and well developed to approximate integrals in high dimension for a long time. However, the number of functions evaluations increasing enormously large make a weak point for such methods. In that situation, adaptive cubature is often preferred choice because of a high efficiency and a low cost of calculation it brings back for the approximation problem. However, the data of the integrated regions and of values of the integrand must be continuous due to the theory of integration. It is infeasible to store in computer memory. To deal with this, the discretization of data for both of the region and the function values are used by constructing the net of the potential mesh points. This technique is acceptable since the result we want to extract is only an approximation within a requisite error. The paper aims to present that technique and some remarkable results.
Keywords: Adaptive Cubature Program, Approximation Techniques, Discretization, Continuous Data
Cite this paper: Dinh Van Tiep, Tran Thi Hue, A Technique of Discretizing Continuous Data for Programming Adaptive Deterministic Cubature Methods in Moderate Dimensions, Applied Mathematics, Vol. 10 No. 1, 2020, pp. 1-6. doi: 10.5923/j.am.20201001.01.
Article Outline
1. Introduction
1.1. Background and Problem Statement
- The algorithm of the Adaptive cubature as well as other methods of numerical integration in high dimension are developed and have been used for a very long time. It definitely has the advantage of accuracy, but also has the drawback of the cost for computation such as the consummation of time and memory since the increasing complexity in calculation. With the help of computers, the implementations of such algorithm in high dimension need to be adjusted. Moreover, in the general case of high dimension, a program for the algorithm have not been provided yet. A primary obstacle of programming the algorithm is the fact that the integrated domain in high dimension with the smooth boundary are described by hypersurfaces which are produced by continuous data of points. Unfortunately, it is impossible to find enough memorized space of hardware to store the data. This makes the algorithm somewhat theoretical and impractical with a tremendous mass of computation. The algorithm itself amends this by a prescribed error, called the tolerance, which requires the accepted estimate error of the approximation must not exceed this tolerance. This reduces quite a lot the number of calculation, but this itself is not enough to make the algorithm feasible to implement because we still need a strategy to store the information we need in the computation process about the values of the integrand on the boundary of the integrated domain.
1.2. Background and Problem Statement
- The cubature is the term introduced by Krommer and Ueberhuber [1,2] to indicate the numerical computation of multiple integral. It includes many techniques such as the Monte Carlo and Quasi-Monte Carlo cubature, Bayesian cubature, adaptive cubature. To adaptive cubature, in 2003, Genz and Cools published an algorithm of adaptive cubature for simplices [3] as well as CUBPACK in FORTRAN90. We knew, in high dimensions, the Monte Carlo cubature is the most preferable choice for a numerical integration because of the advantage in dialing with the curse of dimensionality. But this method only yields, in general, a rate of convergence
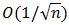 which is quite slow for the number of
which is quite slow for the number of  sample points. Another shortcoming of this method, especially in the case of no permission for using the probability error, is that the order of convergence is only represented in the randomized terms. That is, the estimate error produced by the Monte Carlo method is not deterministic [4] and it is unsuitable if the cubature problem needs a guaranteed error. That is an indirect reason why we still need to invoke the deterministic cubature, especially in a moderate number of dimensions (say, less than 7). The authors Genz and Malik, Berntsen and Espelid and Genz, Dooren and Ridder presented in [5,6,7] their works on the adaptive cubature, however, these were developed on a hyper-cube, which is the simplest region in high dimensions. A natural development for an adaptive cubature on more general region in high dimensions is discussed in this paper.
sample points. Another shortcoming of this method, especially in the case of no permission for using the probability error, is that the order of convergence is only represented in the randomized terms. That is, the estimate error produced by the Monte Carlo method is not deterministic [4] and it is unsuitable if the cubature problem needs a guaranteed error. That is an indirect reason why we still need to invoke the deterministic cubature, especially in a moderate number of dimensions (say, less than 7). The authors Genz and Malik, Berntsen and Espelid and Genz, Dooren and Ridder presented in [5,6,7] their works on the adaptive cubature, however, these were developed on a hyper-cube, which is the simplest region in high dimensions. A natural development for an adaptive cubature on more general region in high dimensions is discussed in this paper.1.3. Contribution
- In this paper, we derive an algorithm for the numerical integration over more general regions which are enclosed by measurable surfaces. In some sense, the storage of data describing the region is another challenge. We cannot store all data of this boundary because it composes continuous surfaces. With the need of a strategy to store the data required for calculation in each iterated step, we establish a net of the stored data with the mesh points become denser on the region over which the estimate error is not less than the corresponding tolerance distributed over this region. The technique is the way of discretizing the continuous data of the integrated region. The extracted phase to get the data is organized in an adaptive way in which only the values needed for calculation in the next iteration are invoked. The introduction of this technique for the general domain of dimension n is the main contribution of the paper. In addition, the creation of data points and well organize them in the form of a net so that we can easily access the data also reveals another challenge to program the general algorithm. In the paper, we propose a solution to this problem by a simple approach using the bisection in not too high dimensions. This approach in such dimensions is useful to simplify the structure of the program and this definitely contributes to speed up the computation process.
1.4. Organization of the Paper
- The paper is divided into 4 section. The second section is intended to briefly describe the basis of the adaptive cubature for approximating the multiple integrals over the quite general region, so called the non-rectangular hyper-boxes. The idea is developed from two specified methods, the Simpson’s rule and the Composite Simpson’s rule with 4 subintervals developed for the multiple integrals. The challenges are not only from the curse of dimensionality, but also from the complicated of the integrated region. For this point, as the aforementioned discussion, the complication in depicting the general region can be overcome in a somewhat temporarily acceptable approach in which we store discretely a set of data points that establish the skeleton of the region. We are not going to use these points all at once, but with the accommodation to fit the requirement each checking time. This does not makes the memory of computer working without overloading. Another benefit of this approach is the same as that of a usual adaptive cubature with the flexibility in subdividing the integrated region by adjusting the size of the sub-regions for the next iteration incorporating with the estimate of the error obtained from the use of the two methods applied at this step.The third section shows off the algorithm of the method which is organized and presented generally in the style of the Matlab language. An illustration for the proper operation of the algorithm is also presented in the case of the dimension 2, the approximation of double integrals. In the last section, we briefly conclude the feature of the algorithm discussed including its advantages and shortcoming.
2. Adaptive Cubature
2.1. Approximation of the Multiple Integrals over Non-rectangular Hyper-boxes
- Consider the problem of approximating multiple integral I of a function
 which is continuously differentiable up to order 4 on a region
which is continuously differentiable up to order 4 on a region 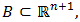 a non-rectangular hyper-box
a non-rectangular hyper-box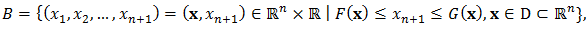
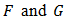 are continuous functions on the rectangular hyper-box
are continuous functions on the rectangular hyper-box 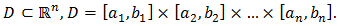 Our aim now is to formulate an approximation for
Our aim now is to formulate an approximation for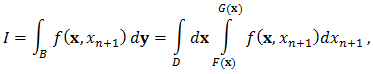 | (1) |
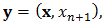 by using the Simpson’s rule and the Composite Simpson’s rule with
by using the Simpson’s rule and the Composite Simpson’s rule with 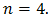 Simpson’s rule. Firstly, the inner integral of (1) is that of one variable, and treated as
Simpson’s rule. Firstly, the inner integral of (1) is that of one variable, and treated as 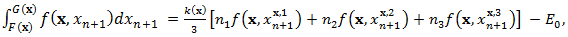 | (2) |
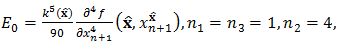
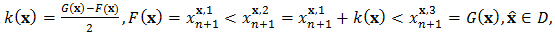 the notation
the notation 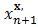 indicates that
indicates that 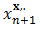 depends on the fixed point
depends on the fixed point 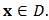 Theorem 1 (Simpson’s rule)
Theorem 1 (Simpson’s rule)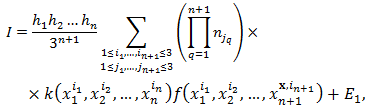 | (3) |
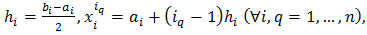 and
and 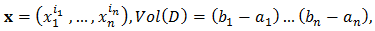
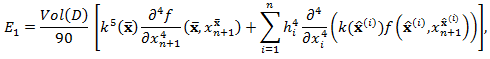 for some
for some 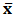 and
and 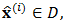 and some
and some 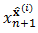 in the interval
in the interval 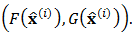 PROOF: Integrate both sides of (2) over
PROOF: Integrate both sides of (2) over 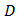 with respect to with the use of Mean Value Theorem for the multiple integral of the term
with respect to with the use of Mean Value Theorem for the multiple integral of the term 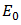 over
over 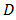 to get
to get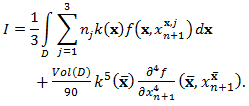 | (4) |
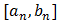 for terms in the sum of the first term of (4), denoting that
for terms in the sum of the first term of (4), denoting that 
 to get the first term of (4) to be
to get the first term of (4) to be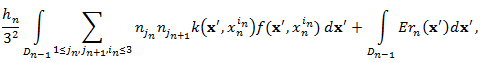 | (5) |
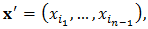 and for some
and for some 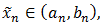
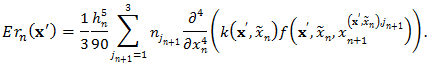 | (6) |
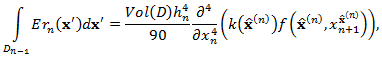 for some
for some 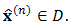 Similarly, reapplying the Simpson’s rule consecutively to other
Similarly, reapplying the Simpson’s rule consecutively to other 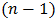 dimensions of
dimensions of 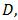 we complete the proof.Composite Simpson’s rule with n=4. Set
we complete the proof.Composite Simpson’s rule with n=4. Set 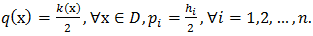 Similar to the above derivation of Simpson’s rule, the following result is obtained for the Composite Simpson’s rule.Theorem 2. (Composite Simpson’s rule) Let
Similar to the above derivation of Simpson’s rule, the following result is obtained for the Composite Simpson’s rule.Theorem 2. (Composite Simpson’s rule) Let 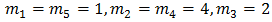 be the coefficients of the Composite Simpson’s rule with
be the coefficients of the Composite Simpson’s rule with 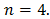 We have,
We have,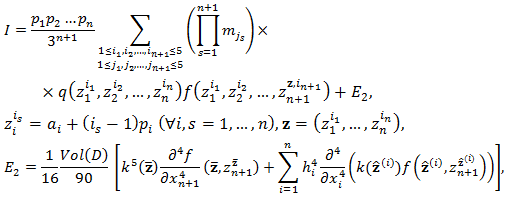 | (7) |
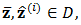 and some
and some 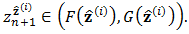
2.2. Adaptive Cubature in High Dimensions
- Let denote
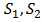 the first term in the right-hand side of (3), (7), respectively. Assume that
the first term in the right-hand side of (3), (7), respectively. Assume that 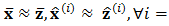
 So,
So, 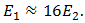 Since
Since 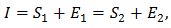 we have
we have 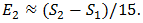 Hence,
Hence,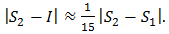 | (8) |
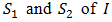 to approximate the error
to approximate the error 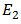 in the approximation revealed by (7). Therefore, we can design the size of the error to be less than a given tolerance
in the approximation revealed by (7). Therefore, we can design the size of the error to be less than a given tolerance 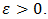 Concretely, if
Concretely, if 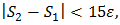 then we could believe that
then we could believe that 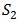 approximates
approximates 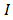 to within
to within 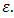 Otherwise, if
Otherwise, if 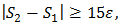 we mostly get wrong when using
we mostly get wrong when using 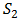 to approximate
to approximate 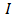 with the error less than
with the error less than 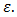 In the latter case, we may get a reasonable approximation by reapplying the above-mentioned procedure on smaller regions (each of such a sub-region has only a size of nearly
In the latter case, we may get a reasonable approximation by reapplying the above-mentioned procedure on smaller regions (each of such a sub-region has only a size of nearly 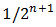 of that of the original region
of that of the original region 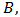 and the expected tolerance for approximation of the integral over that sub-region is only
and the expected tolerance for approximation of the integral over that sub-region is only 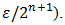 Now in such smaller region, we search for
Now in such smaller region, we search for 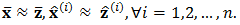 Since the size of such sub-regions becomes smaller and smaller,
Since the size of such sub-regions becomes smaller and smaller, 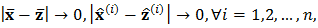 we can eventually reach the target if continuing the procedure. Theoretically, the procedure always succeeds in finding an approximation of
we can eventually reach the target if continuing the procedure. Theoretically, the procedure always succeeds in finding an approximation of 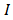 lying to within the given tolerance. However, a computer program cannot execute the procedure in the infinite number of times. Therefore, we set up a limitation for the search by requiring that the level of subdivision (or the number of times in which the procedure is repeated) does not exceed a prior number
lying to within the given tolerance. However, a computer program cannot execute the procedure in the infinite number of times. Therefore, we set up a limitation for the search by requiring that the level of subdivision (or the number of times in which the procedure is repeated) does not exceed a prior number 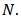 So, the program will reveal the status of failure if
So, the program will reveal the status of failure if 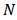 is exceeded. Otherwise, we obtain a desired approximation.
is exceeded. Otherwise, we obtain a desired approximation. 3. Algorithm for the Adaptive Cubature
3.1. Pseudo Matlab Code for the Implementation
- We describe the algorithm for the aforementioned procedure in the form of a pseudo-code with the use of Matlab functions. However, the notations and the structure of the repeat loops or the if-condition, the assignment operator are not the same as those in Matlab. They are changed in order to make the program familiar with the mathematic notations, so it may be simpler to analyse.INPUT region
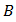 (including
(including 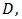 and functions
and functions 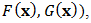 function
function 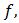 tolerance
tolerance 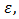 limited level
limited level 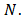 OUTPUT approximation
OUTPUT approximation  or a message announces that the level
or a message announces that the level  is exceeded (that is, the procedure fails!).
is exceeded (that is, the procedure fails!).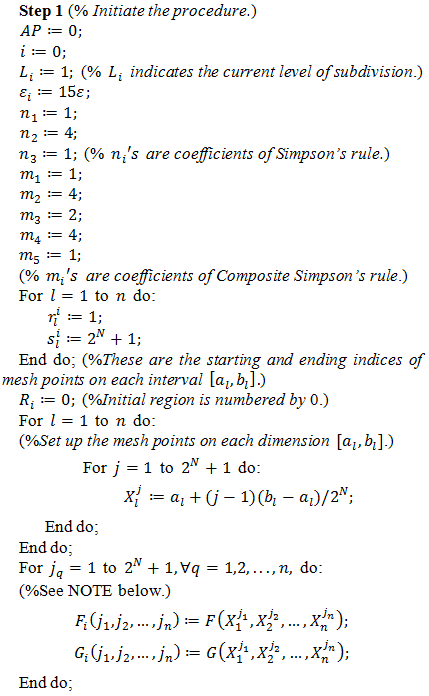
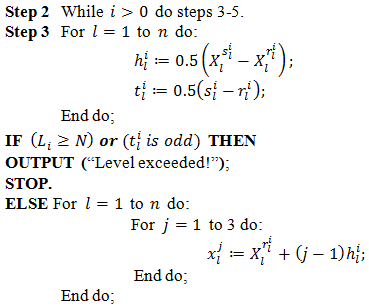
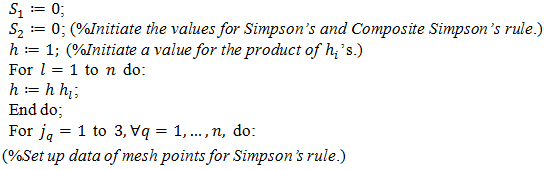
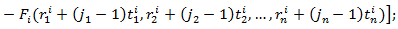
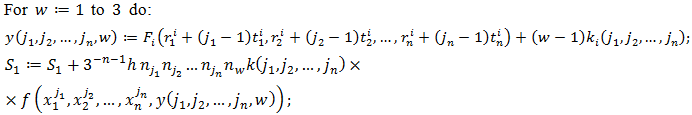
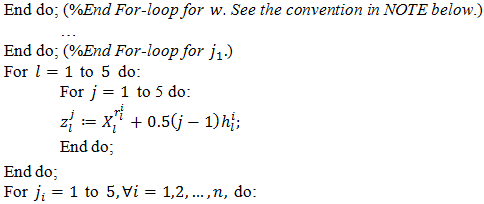
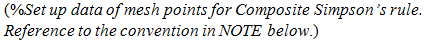
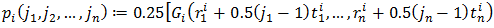
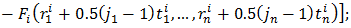
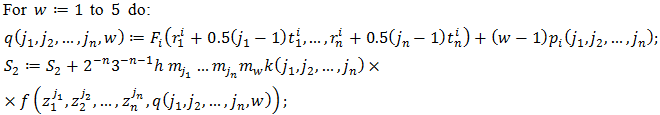




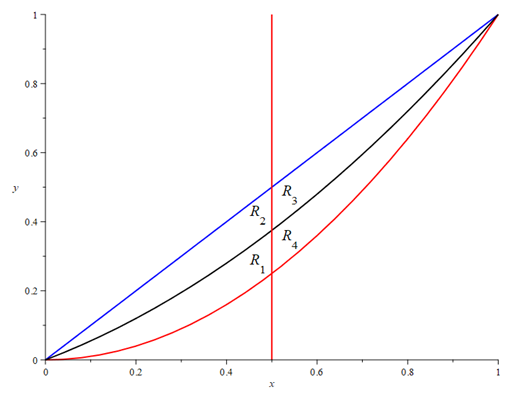 | Figure 1. The region B and its 4 sub-regions in the first iteration step |
3.2. Numerical Example
- Consider the double integral
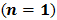
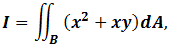 where the non-rectangular region
where the non-rectangular region 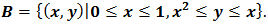 The exact result is
The exact result is 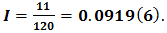 An implementation use the above algorithm yields an approximation
An implementation use the above algorithm yields an approximation 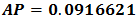 of
of 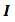 to within the given tolerance
to within the given tolerance 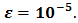 The limit level is
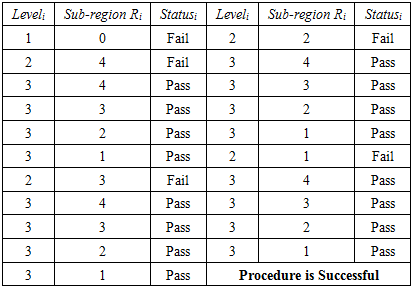
The limit level is 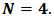 The whole procedure is described in the Table 1.
The whole procedure is described in the Table 1.
|
4. Conclusions
- The algorithm discussed in the paper dials with a basis problem of numerical analysis with a technique which enables to optimize the implementation of the science computers even when the setting of the multiple integration is quite general, a general iterated regions with a continuous multivariable function refer to as the integrand. There are the repeat loops presented in the implementation which are nested loops. To realize each such loop in the program we need to makes the verification with respect to the dimension of the multiple integral. That means, each dimension has a particular program to the corresponding algorithm. Therefore, it is preferable to use the implementation for not too high dimension, say less than 7. For these sizes of dimension, the algorithm take much more advantages of a high speed of convergence comparing to the Monte Carlo and Quasi-Monte Carlo cubature which are preferable choices in very high dimensions.
ACKNOWLEGEMENTS
- The authors are working in Thai Nguyen University of Technology. This work are supported by the university. We are very grateful for this help and other assistance in reaching the references we need to complete this work.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML