C. Nwaigwe, R. I. Ndu, A. Weli
Department of Mathematics, Rivers State University, Port Harcourt, Nigeria
Correspondence to: C. Nwaigwe, Department of Mathematics, Rivers State University, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
We investigate the effects of moving channel wall, thermal radiation and variable-thermal conductivity on the flow of a non-Newtonian fluid in a porous channel. The effects on fluid temperature variations are also studied. By assuming that both the fluid viscosity and thermal conductivity are temperature-dependent, and incorporating viscous dissipation, uniform magnetic field and constant pressure gradient, the governing equations are presented. An implicit-explicit finite difference scheme is formulated and the numerical results are presented and discussed. The results show that near the moving wall, the transport of momentum, from the moving wall into the channel, is retarded by decrease in the fluid viscosity. While the opposite happens -velocity increases with decreasing viscosity- away from the moving wall where the pressure forces dominate the wall shearing forces.
Keywords:
Finite Difference Methods, Variable-viscosity fluid, Thermal radiation, Channel flow, Variable Thermal conductivity, Viscous dissipation
Cite this paper: C. Nwaigwe, R. I. Ndu, A. Weli, Wall Motion Effects on Channel Flow with Temperature-Dependent Transport Properties, Applied Mathematics, Vol. 9 No. 3, 2019, pp. 162-168. doi: 10.5923/j.am.20190903.04.
1. Introduction
Many engineering applications involve some moving and/or stationary parts that sandwich some (viscous) fluid; an example is in fluid bearings. The moving parts and other sources, like thermal radiation and frictions between fluid layers (viscous dissipation), can cause some heat variations within the fluid. These temperature variations might in turn lead to some change in the fluid properties, especially the viscosity which are generally not temperature-independent, hence may alter the desired state of the system. It is therefore important to investigate the effects of moving walls and transport properties on the flow of fluid and heat distribution in a channel where one of the walls is moving and the fluid has temperature-dependent properties.Fluid flow and heat transfer in a porous medium has significant importance in industrial applications such as chemical processing equipment, exchangers, polymer extrusion, magnetic material extract, geophysics and cooling rate control (Raju and Sandeep 2016). They also play important roles in ground water hydrology, insulation engineering, grain storage devices, ground water pollution, purification processes and petroleum reservoirs. Non-Newtonian fluids are useful in the chemical process engineering, geothermal engineering, storage of nuclear waste materials and petroleum production (Elgazery 2008). These and many other applications have attracted many researchers to the study of heat and mass transfer in non-Newtonian porous media flows.Loenko et al. (2019) investigated thermogravitational convection of a non-Newtonian fluid in a closed square cavity with a local heat source and showcased their results in the form of isolines of stream function and temperature. It was observed that increase in Raleigh number transforms the heat transport process from conductive to convective, whereas increase in the average Nusselt number reduces heat from the heater surface. Nwaigwe (2010) investigate the evolution of temperature distribution in the ground taking into account the effects of suction and thermal radiation.Prasad et al. (2018) studied the flow and heat transfer in a Casson liquid over a porous vertical heated stretching plates with time-dependent temperature. Nonlinear equations were derived and solved using a semi-analytical approach. It was discovered that suction decreases the velocity boundary layer thickness, while the infusion/blowing increases the velocity. Ratchagar and Vijayakumar (2017) investigated the Hydromagnetic free and forced convection in a parallel plate channel bounded by porous bed and transverse magnetic field.Shit et al. (2016) examined an electrosmotically driven MHD flow and heat transfer in a microchannel. The magnetic field and heating joule were considered as a contributing factor to the control of the fluid and the potential electric field aided the flow. Raju and Sandeep (2016) carried out a numerical study on the flow coupled with heat and mass transfer effects in a vertical rotating cone/plate in porous medium, presenting solutions for thermo diffusion and diffusion- thermo effects using RungeKuttaFelhberg integration scheme. Their results showed that an increase in the magnetic field parameter increases the heat and mass transfer rates, while Soret and Dufour parameters also enhance the heat and mass transfer rates. The work of Raju et al. (2015) examined an unsteady MHD free convection, heat and mass transfer flow of a Newtonian flow past boundless vertical plate with homogeneous chemical reaction and heat absorption. Choudhary et al. (2015) investigated the unsteady MHD flow and heat transfer over an expanding permeable surface with suction using a fourth-order Runge-Kutta method.Celik and Mobedi (2015) studied the effects of an inserted porous layer on the heat and fluid flow in a vertical channel with mixed convection. The impart of buoyancy in the clear fluid region reduces with increment in the thermal conductivity and as a result of this downward the flow reduces. Arthur and Seini (2014) investigated the problem of hydro- magnetic stagnation point flow of a fluid towards a stretching sheet in the presence of radiation and viscous dissipation using Newton-Raphson shooting method along with a fourth-order Runge-Kutta integration algorithm and discovered that increasing the radiation parameter increases the temperature profiles as a result of radiative heating. Vajravelu et al. (2013) examined, numerically, the effects of variable thermal conductivity, thermal radiation and thermal buoyancy on the unsteady flow over a vertical porous stretching sheet. Qasim (2013) examined the combined effects of heat and mass transfer in Jeffrey fluid over a stretching sheet in the presence of heat source/heat sink. It is found that an increase in the heat sink parameter results decreased temperature. It is also observed that boundary layer thickness decreases by increasing Schmidt number.Misra et al. (2008) developed a suitable numerical method to solve a problem of the flow of an incompressible viscoelastic and electrically conducting fluid coupled with heat transfer in between horizontal parallel plates. Ellahi and Riaz (2010) used homotopy analysis method (HAM) to investigate the the influence of MHD on pipe flow of a thirdgrade fluid with variable viscosity. Elgazery (2008) carried out a numerical study on the problem of unsteady free convection with heat and mass transfer from an isothermal plate to a non-Newtonian fluid saturated with porous material. Kim (2000) analyzed unsteady MHD convective heat transfer past a semi-infinite vertical porous moving plate with variable suction and over a plate moving with steady velocity. Recently, Nwaigwe et al. (2019) incorporated double diffusion into channel flows, and the numerical analysis of channel flow is conducted in Nwaigwe (2019).Chinyoka and Makinde (2015) investigated the flow of a non-isothermal fluid with temperature-dependent viscosity in a vertical channel filled with porous material. It is found that the presence of uniform suction/injection reduces the generation of heat and significant delay in the increase of temperature. The purpose of the present paper is to extend the work in Chinyoka and Makinde (2015) by incorporating non-stationary channel wall, radiative heat transfer, variable thermal conductivity, transverse magnetic field, and non-stationary channel plate. We also consider a horizontal channel with the fluid not initially rest. Moreover, we propose a semi-implicit finite difference numerical scheme for the resulting coupled partial differential equations (PDEs). Our scheme decouples the coupled PDEs by treating nonlinear and coupled terms in an explicit manner and discretizes the viscous and thermal conductivity terms in a conservative manner (Nwaigwe 2020). The advantage of this scheme over the extended work is that the present scheme avoids differentiation of coefficients which may not actually exist; and it is also computationally less expensive than the previous.The remainder of the paper is organised as follows. In section 2. we present the mathematical models both in dimensional and non-dimensional forms. The numerical method is formulated in section 3. while the results are presented and discussed in section 4. and the paper is concluded in section 5..
2. Mathematical Formulation of the Problem
Figure 1 shows a horizontal channel of width h meters which is filled with a fluid-saturated porous material. The width lies along the y'-axis and the length along the x'-axis. The wall at y' = 0 is im-movable and perfectly insulated, while the other wall at y' = h moves at a constant velocity, 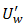 and maintained at a constant temperature,
and maintained at a constant temperature, 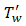 . We consider the flow of a temperature-dependent-viscosity non Newtonian incompressible fluid within the domain.
. We consider the flow of a temperature-dependent-viscosity non Newtonian incompressible fluid within the domain. 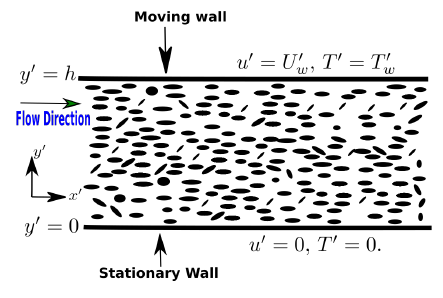 | Figure 1. Physical set up |
Further assume that the fluid is thermal radiating with temperature-dependent thermal conductivity and viscous dissipation is significant. The flow is assumed to be driven by both the pressure gradients and shearing effects occasioned by the mobile wall. A uniform magnetic field is applied on the channel walls and the ensuing flow is unsteady. Assuming a fully developed flow, then the x' component of the fluid velocity, u'(y, t) and temperature T'(y, t) at the distance, y', measured from the stationary wall, at time, t are governed by the following initial-boundary value problem (see Chinyoka and Makinde (2015), Nwaigwe (2020), Selvi and Muthuraj (2017), Nwaigwe and Makinde (2019)):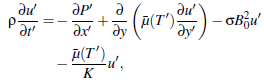 | (1) |
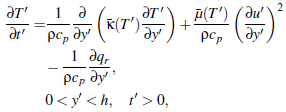 | (2) |
subject to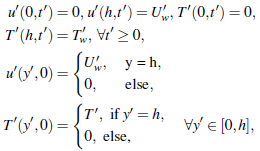 | (3) |
where 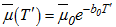 and
and 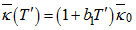 are the fluid’s temperature-dependent viscosity and thermal conductivity respectively, while
are the fluid’s temperature-dependent viscosity and thermal conductivity respectively, while 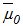 and
and 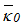 are their constant average values; b0 and b1 are variation constants. Also, ρ = fluid density, P' = fluid pressure, K = permeability of porous medium, σ = electrical conductivity, B0 = uniform magnetic field intensity, cp = specific heat capacity, while qr is the heat flux due to radiation.
are their constant average values; b0 and b1 are variation constants. Also, ρ = fluid density, P' = fluid pressure, K = permeability of porous medium, σ = electrical conductivity, B0 = uniform magnetic field intensity, cp = specific heat capacity, while qr is the heat flux due to radiation.
2.1. Non-Dimensional Equations
We define the following non-dimensional variables and variables and parameters: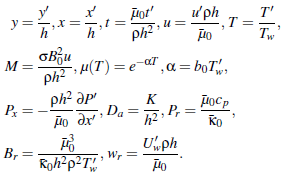 | (4) |
Using (4), then the problem defined in (1) - (3) becomes: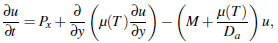 | (5) |
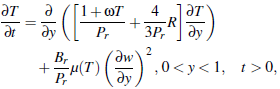 | (6) |
subject to: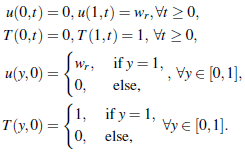 | (7) |
In the above non-dimensional problem, Px is the pressure gradient parameter, a is the viscosity parameter, M is the magnetic field parameter, Da is the Darcy number, Pr the Prandtl number, ω the thermal conductivity parameter, Br the Brinkman number and wr is the non-dimensional wall velocity. This completes the mathematical statement of the problem.
3. Numerical Formulation of the Problem
We choose 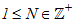 , and define
, and define 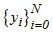 such that
such that 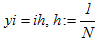 and
and  0,1,2, where
0,1,2, where 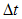 is given. Then we seek to compute the following approximations
is given. Then we seek to compute the following approximations 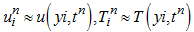 . We also define the operators:
. We also define the operators: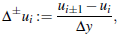 and let
and let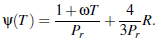 | (8) |
Finally, for any function 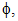 we define
we define 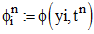 and
and 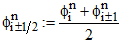 . Then, we consider the following scheme, see Samarskii (2001), Matus (2014)’ Morton and Mayers (2005), Nwaigwe (2020), Nwaigwe and Makinde (2019):
. Then, we consider the following scheme, see Samarskii (2001), Matus (2014)’ Morton and Mayers (2005), Nwaigwe (2020), Nwaigwe and Makinde (2019):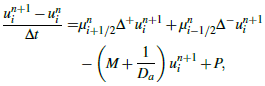 | (9) |
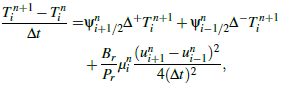 | (10) |
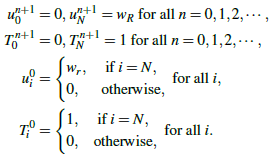 | (11) |
In the above scheme, we treated the coupling terms explicitly and also the variable transport properties. These make the algebraic systems to be solved at any new time step tn+1 to be decoupled and linear, hence each can be solved independently, see Chinyoka and Makinde (2015), Nwaigwe (2020). We present the numerical results in the next section.
4. Numerical Results
In this section, we present the numerical results. The formulated numerical scheme in the previous section is implemented in a C++ code which is developed by the first author.
4.1. Velocity Variations
Figure 2 shows the effect of the viscosity parameter on the fluid velocity. The results indicate that increasing the viscosity parameter (decreasing the viscosity) decreases the flow towards the moving wall (see figure 2(a)) but increases the flow away from the moving wall (see figure 2(b)). This is perfectly expected because of the following: near the moving wall, the flow is mainly driven by the shearing forces generated by the motion of the wall, but away from it (near the stationary wall), the flow is mostly driven by pressure gradients. A decrease in viscosity decreases the effects of shearing forces, thereby decreasing the velocity in the vicinity of shear-driven flow - near the moving wall. On the other hand, a decrease in the viscosity increases the effects of the pressure forces, hence increases the flow away from the moving wall (or near the stationary wall) where the flow is driven by pressure. This leads to the observed (i) decrease of the flow near the moving wall (region of shear-driven flow) and (ii) increase in the flow away from the wall (pressure-driven region).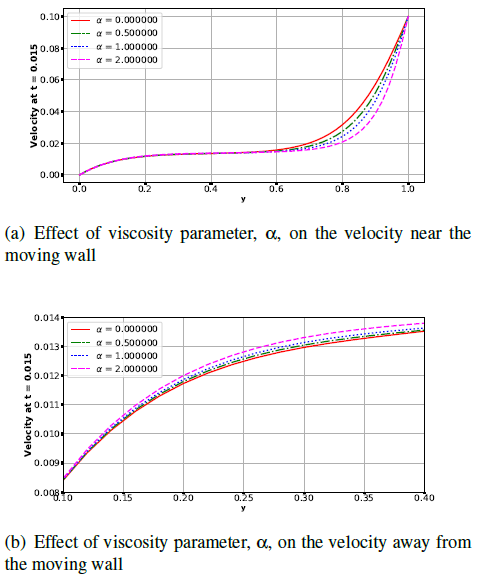 | Figure 2. Effect of viscosity parameter on the velocity |
Figure 3 displays the effect of the wall velocity on the fluid velocity. We can observe that the fluid velocity increases with increase in the wall velocity. This is also physically expected because the viscosity is unchanged, hence the determining factor for the shearing effects on the flow is solely the wall velocity which ultimately increases the velocities.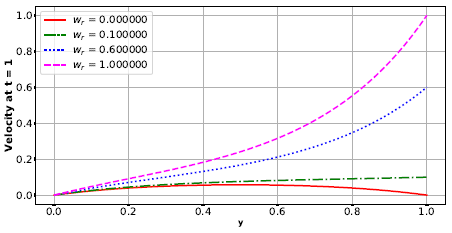 | Figure 3. Effect of wall velocity, wr, on the velocity |
The effects of Darcy number and Magnetic field parameter are depicted in figure 4. It is observed that the velocity increases with increasing Darcy number but decreases with increasing magnetic field parameter. These results are in agreement with previous results such as those of (Nwaigwe and Makinde 2019).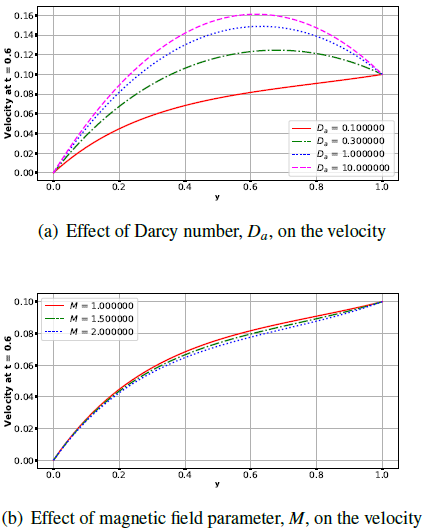 | Figure 4. Effects of Darcy number, Da and magnetic field parameter, M on the velocity |
4.2. Temperature Variations
Figures 5 - 6 display the variations of temperature with respect to thermal conductivity, radiation parameter and the Prantl number. It is found that the temperature increases with increasing thermal conductivity and radiation parameter but decreases with increasing Prandtl number. These results are also realistic because the thermal conductivity measures the ease with which the fluid conducts heat. So, increasing it will facilitate the rate of heat transfer from the heated wall (which is maintained at a constant temperature of unity) into the fluid. On the other hand, increasing the Prandtl means to decrease both the heat generated due to viscous dissipation and the heat transfer rate from the wall, hence the observed decrease in temperature in 6(b).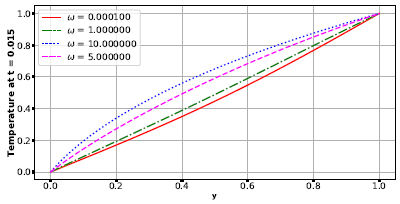 | Figure 5. Effect of thermal conductivity parameter, ω, on the temperature |
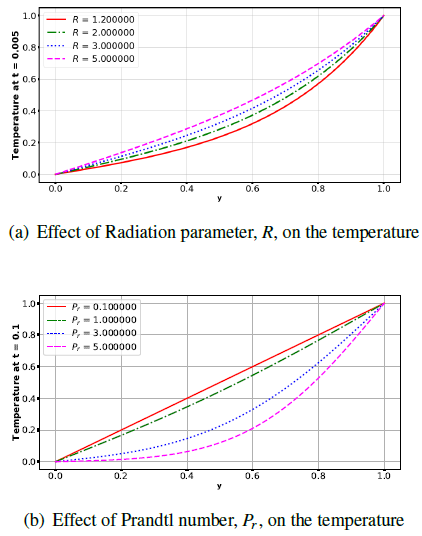 | Figure 6. Effects of Radiation parameter, R and Prandtl number, Pr on the temperature |
4.3. Variation of Skin Friction
Figure 7 shows the effect of viscosity and the wall velocity on skin friction. Skin friction decreases with increase in viscosity parameter near the moving wall, but farther away from the moving plate skin friction increases significantly with increasing viscosity parameter (see figure 7(a)). However, skin friction effect decreases with increase in wall velocity. This effect is also noted to be obvious at some points farther away from the plate (see figure 7(b)). Physically, this is as a result of the downward shear drag acting on the fluid due to the moving plate.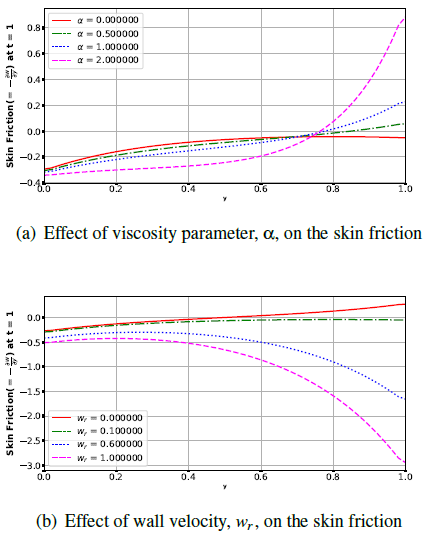 | Figure 7. Effects of viscosity parameter, α, and wall velocity, wr, on the skin friction |
Figure 8 depicts the effect Darcy number and magnetic field on skin friction. The results show that about 0.58 units away from the plate skin friction decreases with increasing Darcy number but above that value the skin friction increases with increasing Darcy number while skin friction increases slightly with increasing magnetic parameter near the plate. This is so because of Lorentz force but effect is lesser away from the plate.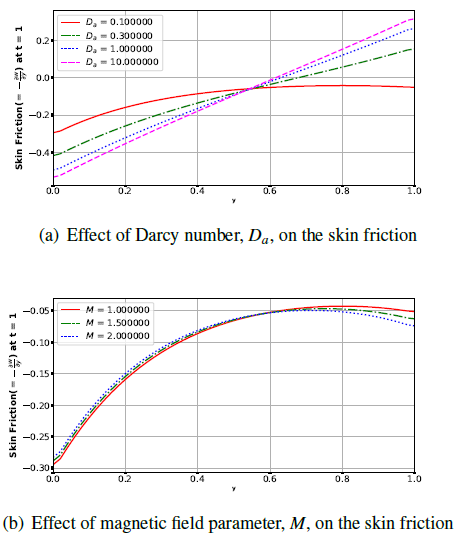 | Figure 8. Effects of Darcy number, Da and magnetic field parameter, M on the skin friction |
4.4. Variation of Nusselt Number
Figure 9 effect of thermal conductivity on Nusselt number. Nusselt number decreases significantly with increasing thermal conductivity parameter near to the plate but increased with increasing thermal conductivity parameter at some distance away from the plate.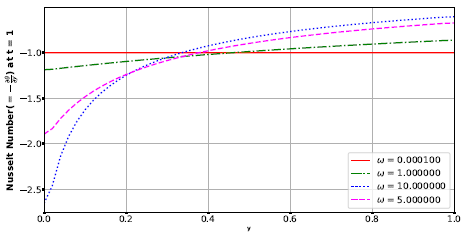 | Figure 9. Effect of thermal conductivity parameter, ω, on the Nusselt number |
Figure 10 displays effect of radiation and Prandtl number on Nusselt number. The Nusselt number increases with increase in radiation parameter but decreases with increasing Prandtl number.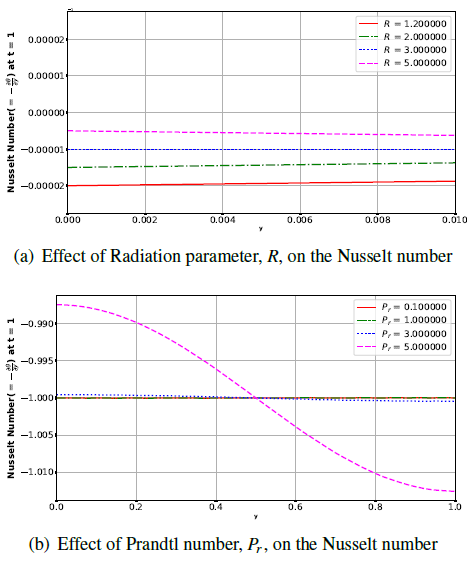 | Figure 10. Effects of Radiation parameter, R and Prandtl number, Pr on the Nusselt number |
5. Conclusions
The fluid flow and heat transfer in a horizontal porous channel with a moving wall, variable transport properties, viscous dissipation and thermal radiation have been investigated. The resulting system of nonlinear partial differential equations is solved using an implicit-explicit finite difference method. The numerical results show that:• At constant fluid viscosity, the increase in the motion of the channel wall increases the fluid velocity throughout the channel.• At constant channel wall velocity, decreasing the viscosity decreases the fluid velocity near the mobile wall where the wall shearing forces dominate pressure forces, whilst this increases the fluid velocity near the stationary wall where pressure forces are dominant.• Increasing the thermal radiation parameter increases the temperature and• Increase in the thermal conductivity parameter increases the temperature.
ACKNOWLEDGMENTS
The first author is grateful to the PTDF for sponsoring his PhD at the University of Warwick during 2012-2016.
References
| [1] | Arthur, E. M. and I. Y. Seini (2014). Hydromagnetic stagnation point flow over a porous stretching surface in the presence of radiation and viscous dissipation. Applied and Computational Mathematics 3(5), 191–196. |
| [2] | Celik, H. and M. Mobedi (2015). Effect of an inserted porous layer on heat and fluid flow in a vertical channel with mixed convection. Thermal Science 19(3). |
| [3] | Chinyoka, T. and D. O. Makinde (2015). Unsteady and porous media flow of reactive non-newtonian fluids subjected to buoyancy and suction/injection. International Journal of Numerical Methods for Heat & Fluid Flow 25(7), 1682–1704. |
| [4] | Choudhary, M. K., S. Chaudhary, and R. Sharma (2015). Unsteady mhd flow and heat transfer over a stretching permeable surface with suction or injection. Procedia Engineering 127, 703–710. |
| [5] | Elgazery, N. S. (2008). Transient analysis of heat and mass transfer by natural convection in power law fluid past a vertical plate immersed in a porous medium (numerical study). Applications and Applied Mathematics 3(2), 267–285. |
| [6] | Ellahi, R. and A. Riaz (2010). Analytical solutions for mhd flow in a third-grade fluid with variable viscosity. Mathematical and Computer Modelling 52(9-10), 1783–1793. |
| [7] | Kim, Y. J. (2000). Unsteady mhd convective heat transfer past a semi-infinite vertical porous moving plate with variable suction. International journal of engineering science 38(8), 833–845. |
| [8] | Loenko, D. S., A. Shenoy, and M. A. Sheremet (2019). Natural convection of nonnewtonian power-law fluid in a square cavity with a heat-generating element. Energies 12(11), 2149. |
| [9] | Matus, P. (2014). On convergence of difference schemes for ibvp for quasilinear parabolic equations with generalized solutions. Computational Methods in Applied Mathematics 14(3), 361–371. |
| [10] | Misra, J., G. Shit, and H. J. Rath (2008). Flow and heat transfer of a mhd viscoelastic fluid in a channel with stretching walls: Some applications to haemodynamics. Computers & Fluids 37(1), 1–11. |
| [11] | Morton, K. W. and D. F. Mayers (2005). Numerical solution of partial differential equations: an introduction. Cambridge university press. |
| [12] | Nwaigwe, C. (2010). Mathematical modelling of ground temperature with suction velocity and radiation. American Journal of Scientific and Industrial Research 1(2), 238–241. |
| [13] | Nwaigwe, C. (2019). Analysis and application of a convergent difference scheme to nonlinear transport in a brinkman flow. International Journal of Numerical Methods for Fluid and Heat Flows In Print. |
| [14] | Nwaigwe, C. (2020). Sequential implicit numerical scheme for pollutant and heat transport in a planepoiseuille flow. Journal of Applied and Computational Mechanics 6(1), 13–25. |
| [15] | Nwaigwe, C. and O. D. Makinde (2019). Finite difference investigation of a polluted non-isothermal non-newtonian porous media flow. Accepted by Defect and Diffusion Forum special issue on Engineering Fluid Flows and Heat Transfer Analysis. |
| [16] | Nwaigwe, C., A. Weli, and O. D. Makinde (2019). Computational analysis of porous channel flow with cross-diffusion. American Journal of Computational and Applied Mathematics 9(5), 119–132. |
| [17] | Prasad, K., K. Vajravelu, H. Vaidya, M. Rashidi, and Z. B. Neelufer (2018). Flow and heat transfer of a casson liquid over a vertical stretching surface: Optimal solution. Ameri- can Journal of Heat and Mass Transfer 5(1), 1–22. |
| [18] | Qasim, M. (2013). Heat and mass transfer in a jeffrey fluid over a stretching sheet with heat source/sink. Alexandria Engineering Journal. |
| [19] | Raju, C. S. and N. Sandeep (2016). Heat and mass transfer in mhd non-newtonian bio- convection flow over a rotating cone/plate with cross diffusion. Journal of molecular liquids 215, 115–126. |
| [20] | Raju, M., M. Umamaheswar, and S. Varma (2015). Analysis of mhd transient free convection flow of a newtonian fluid past an infinite vertical porous plate. Frontiers in Heat and Mass Transfer (FHMT) 6(1). |
| [21] | Ratchagar, N. P. and R. Vijayakumar (2017). Effect of buoyancy and magnetic field on unsteady convective diffusion of solute in a boussinesq stokes suspension bounded by porous beds. Applications & Applied Mathematics 12(1). |
| [22] | Samarskii, A. A. (2001). The theory of difference schemes. New York: Marcel Dekker. |
| [23] | Selvi, R. and R. Muthuraj (2017). Mhd oscillatory flow of a jeffrey fluid in a vertical porous channel with viscous dissipation. Ain Shams Engineering Journal. |
| [24] | Shit, G., A. Mondal, A. Sinha, and P. Kundu (2016). Electro-osmotically driven mhd flow and heat transfer in micro-channel. Physica A: Statistical Mechanics and its Applications 449, 437–454. |
| [25] | Vajravelu, K., K. Prasad, and C.-O. Ng (2013). Unsteady convective boundary layer flow of a viscous fluid at a vertical surface with variable fluid properties. Nonlinear Analysis: Real World Applications. |


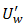 and maintained at a constant temperature,
and maintained at a constant temperature, 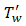 . We consider the flow of a temperature-dependent-viscosity non Newtonian incompressible fluid within the domain.
. We consider the flow of a temperature-dependent-viscosity non Newtonian incompressible fluid within the domain. 
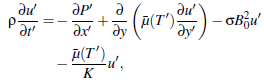
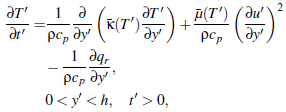
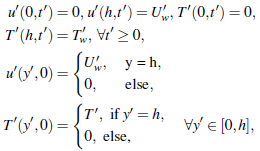
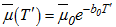 and
and 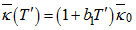 are the fluid’s temperature-dependent viscosity and thermal conductivity respectively, while
are the fluid’s temperature-dependent viscosity and thermal conductivity respectively, while  and
and  are their constant average values; b0 and b1 are variation constants. Also, ρ = fluid density, P' = fluid pressure, K = permeability of porous medium, σ = electrical conductivity, B0 = uniform magnetic field intensity, cp = specific heat capacity, while qr is the heat flux due to radiation.
are their constant average values; b0 and b1 are variation constants. Also, ρ = fluid density, P' = fluid pressure, K = permeability of porous medium, σ = electrical conductivity, B0 = uniform magnetic field intensity, cp = specific heat capacity, while qr is the heat flux due to radiation.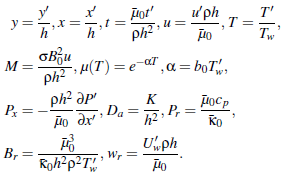
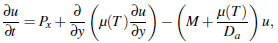
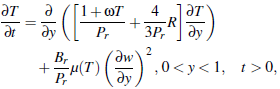
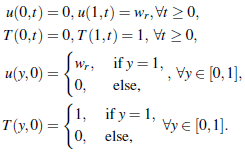
 , and define
, and define 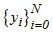 such that
such that 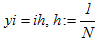 and
and  0,1,2, where
0,1,2, where 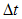 is given. Then we seek to compute the following approximations
is given. Then we seek to compute the following approximations 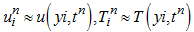 . We also define the operators:
. We also define the operators: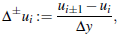 and let
and let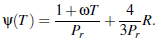
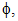 we define
we define 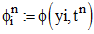 and
and 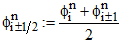 . Then, we consider the following scheme, see Samarskii (2001), Matus (2014)’ Morton and Mayers (2005), Nwaigwe (2020), Nwaigwe and Makinde (2019):
. Then, we consider the following scheme, see Samarskii (2001), Matus (2014)’ Morton and Mayers (2005), Nwaigwe (2020), Nwaigwe and Makinde (2019):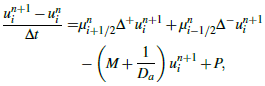
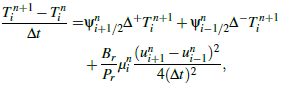
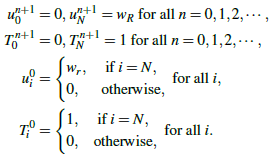









 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML