-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2019; 9(3): 89-161
doi:10.5923/j.am.20190903.03
Fundamental Concepts of Geometry
Abstract
Reference
Full-Text PDF
Full-text HTMLKassahun Tesfaye Agzew
Department of Mathematics, College of Natural and Computational Sciences, Wolkite University, Wolkite, Ethiopia
Correspondence to: Kassahun Tesfaye Agzew , Department of Mathematics, College of Natural and Computational Sciences, Wolkite University, Wolkite, Ethiopia.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Euclidean Geometry is a mathematical system attributed to Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, [1] Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. [2] The Elements begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language. [1] For more than two thousand years, the adjective Euclidean was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious (with the possible exception of the parallel postulate) that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's theory of general relativity is that physical space itself is not Euclidean, and Euclidean space is a good approximation for it only over short distances (relative to the strength of the gravitational field). [3] Euclidean geometry is an example of synthetic geometry, in that it proceeds logically from axioms describing basic properties of geometric objects such as points and lines, to propositions about those objects, all without the use of coordinates to specify those objects. This is in contrast to analytic geometry, which uses coordinates to translate geometric propositions into algebraic formulas.
Keywords: Point, Line, Plane, Euclidean Geometry, Hyperbolic Geometry, The Consistency of Euclidean Geometry
Cite this paper: Kassahun Tesfaye Agzew , Fundamental Concepts of Geometry, Applied Mathematics, Vol. 9 No. 3, 2019, pp. 89-161. doi: 10.5923/j.am.20190903.03.
Article Outline
1. Absolute Geometry
1.1. Introduction
- We shall be concerned mainly with Geometry, like arithmetic, requires for its logical development only a small number of simple, and fundamental principles. These fundamental principles are called the Axioms Of Geometry. The choice of the axioms and the investigation of their relation to one another is a problem which, since the time of Euclid, has been discussed in numerous excellent memories to be found in the mathematical literature.Geometry is a science of shape, size and symmetry. While arithmetic dealt with numerical structures, geometry deals with metric structures. Geometry is one of the oldest mathematical disciplines and early geometry has relations with arithmetic. Geometry was also a place, where the axiomatic method was brought to mathematics: Theorems are proved from a few statements which are called axioms.Absolute Geometry is a geometry which depends only on the first four of Euclid’s postulates and not on the parallel postulates. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulates.Let us consider three distinct systems of things. The things composing the first system, well will call points and designate them by the letter A, B, C, those of the second, we will call straight lines designate them by the letters a, b, c, and those of the third system and we will call planes and designate them by the Greek letters
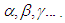The points are called the elements of linear geometry; the points and straight lines, the elements of plane geometry; and the points, lines, and planes, the elements of the geometry of space or the elements of space.We think of these points, straight lines, and planes as having certain mutual relations, which we indicate by mean of such word as “are situated”, “between”, “parallel”, “congruent”, “continuous”, etc. the complete and exact description of these relations follows as a consequence of the axioms of geometry. These axioms may be arranged in five groups. Each of these groups expressed, by itself, certain related fundamental fact of our intuition. I. Axioms of incidence (connection)II. Axioms of betweenness (order)III. Axioms of parallel (Euclid’s axiom) IV. Axioms of congruence V. Axioms of continuity Although point, line and plane etc. do not have normal definition, we can describe them intuitively as follows. Point: We represent points by dot and designate them by capital letters. (See figure 1.1.1). Line: We represent lines by the indefinitely thin and long mark. Lines are designated by small letters. We regard lines as a set of points that can be extended as far as desired in either direction (See figure 1.1.2).Plane: We think of a plane as a flat surface that has no depth (or thickness). We designate planes by Greek letters 
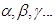and represent it by some appropriate figure in space. (See figure 1.1.3)