1. Introduction

Finding the optimal route in Networks (transport work, telecommunication network, etc) is the most common task of Graph Theory in our everyday life. These tasks are solved with in the model of the transport networks an example of non-oriented, connected and edge-rated graph. We are searching for optimal routes at this graph (Model) because we need, for example to minimize the costs necessary for realization of journeys. Minimizing the cost (such as the fuel consumption) can be understood as a task of finding the shortest (minimal) path between two specified nodes in the graph.

But it is not always about the minimizing of costs, task of the reliability and capacity belong to the issue of route optimization in networks as well. These examples belong to the tasks of important route within the graph:

1. Task of the shortest (minimal) path;

− From one specific node of graph (origin) to another;

a) Searching for minimal path from origin to final destination;

b) Searching for minimal path from origin to all other nodes of graph;

− From each node to another;

2. Task of the most reliable path;

3. Path with maximum capacity;

4. Finding the maximum path in the graph (adjusted general algorithm).

In the following part a task of optimal route is generally formulated and a practical demonstration of the application of a simplified Floyd’s algorithm on the transport network of I and II class roads in the Knust, Kumasi is conducted for searching optimal routes in the network. Specifically, it is the application of the algorithm in the task of finding the minimal path from each of the network vertex to another.

SOME NETWORK DEFINITIONS

A network consists of a set of points and a set of lines connecting certain pair of the points. These points are called nodes and are linked by arcs, edges or branches. Associated with each arc is the flow of some type. In a transportation network, cities represent nodes and highways represent edges or arc, with traffic representing arc flow. The standard notation for describing network G= (N, A) where N is the set of nodes and A is the set of edges or arcs

N = {1, 2, 3, 4, 5}

A = {(1, 3), (1, 2),(2, 3),(2, 4),(2, 5),(3, 4),(3, 5),(4, 5)}

The network in the figure above has nodes designated by five (5) circles. The lines in the figure represent the edges. As an illustration, the figure below has seven (7) arcs corresponding to the seven (7) roads in the road system in the figure 1.

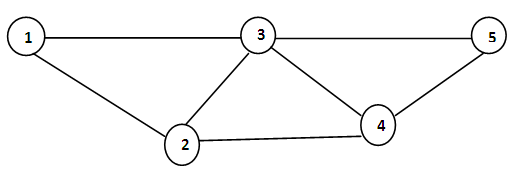Figure 1

An arc is said to be directed or oriented if it allows positive flow in one direction and zero flow in the opposite direction. A path is a sequence of distinct arcs that joins the two nodes regardless of the orientation of the individual arcs. For example, in the figure above (1.3), (3, 2) and (2, 4) represent a path from node 1 to node 4. Again a path will form a loop or a cycle if it connects a node to itself. For example, in the above figure, the arcs (2, 3), (3, 4) and (4, 2) form loop. A directed loop (or a circuit) is a loop in which all the arcs have the same direction or orientation. A connected Network is network in which every two distinct nodes are linked by a path as demonstrated in the figure. Also a direct network has a network with all directed arcs.

Today it is possible to determine the faster route and dispatch the immediate assistance or with the help of the assistance of Geological Information System (G.I.S). With the advance development in technology, the analyses of networking and transportation within the technological location must become a common practice in many applicable areas. The key problem in network and transportation is the calculation of the SHORTEST PATHS between different locations on a network Sometimes this calculation has to be done in real times.

For the sake of illustration, let us have a look at the case of an emergency call, ask for an ambulance to rush a patient from a very remote area to a hospital. Because a linkage on a real road network in the metropolitan tends to posse different levels of overcrowding during different time period of a day and because a Patient’s location cannot be expected to be known in advance, it is practically impossible to decide the fastest route before a call is received. Hence the fastest route can only be resolute in real time. In some cases the fastest route has to be determined in a few second in order to ensure the safety of a patient. Furthermore when large real road network are involved in an application, the determination of SHORTEST PATHS on a large network can be computationally very intensively. The collection, transport and disposal of solid waste, which is a highly visible and important municipal service, involves a large expenditure but receives, scant attention. This problem is even more crucial for large cities in developing countries due to the hot weather.

A constructive heuristic, which takes into account the environmental aspect as well as the cost, is proposed to solve the routing aspect of garbage collection. This is based on a look-ahead strategy, which is enhanced by two additional mechanisms;

1. The problem and its impact on the environment collection of household refuse/industrial waste is one of the most difficult operational problems faced by local authorities in any large city. The collection problem is especially crucial for cities in developing countries. Solid wastes generated from urban and industrial sources also contain a large number of ingredients, some of which are toxic.

2. Related work, the waste collection problem can be modeled as the Capacitated Arc Routing Problem (CARP). As this problem cannot be solved by optimal (exact) methods in practice, heuristics are used for this purpose. One possible approach is first to find a giant tour and then decompose it into a set of routes that are feasible with regard to the vehicle capacity. More importantly in the inspection of distributed systems such as electric poles, gas pipeline telephone line and a whole lot more so as faults to be rectify as soon as possible.

Because many applications involves real networks and also since the calculation of a fastest route (shortest path) necessitates an answer in real time a natural question to ask is which shortest path runs fastest on real road networks? Although there are a number of shortest path algorithms such as Djikstra’s, Floyd’s, Glover et al Goldberg and Radzik etc. But there is no clear answer as to which algorithm, or a set of algorithms runs faster on a real road network.

2. Chapter Two

SHORTEST PATH ALGORITHMS

Shortest path problems are the most fundamental and the most commonly encountered problems in the study of transportation and communication network [1]. There are many types of shortest –path problems. For example, we may be interested in determining the shortest path (i.e., the most economic path or fastest path, or minimum –fuel –consumption path) from one specified node in the network to another specified node; or we may need to find shortest paths from a specified node to all other nodes. Shortest paths between all pairs of nodes in a network are required in some problems. Sometimes, one wishes to find the shortest path from one given node to another given node that passes through certain specified intermediate nodes. In some applications, one required not only the shortest path but also the second and third shortest path. There are instances when the actual shortest path is not required, but only the shortest distance is required. Next, we shall confine ourselves to two most important shortest-path problems:

1. How to determine shortest distance (a shortest path) from a specified node to another specified node, and

2. How to determine shortest distances (and paths from every node to every other node in the network.)

ALL – PAIRS SHORTEST PATH PROBLEM

The shortest path between two nodes might not be a direct edge between them, but instead involve a detour through other nodes. The all- pairs shortest path problem requires that we determine shortest path distances between every pair of nodes in a network. Shortest path problems are the most fundamental and the most commonly encountered problem in the study of transportation and communication networks [1]. There are many types of shortest-path problem. For example, we may be interested in determining the shortest path (i.e., the most economical path or fastest path, or minimum-fuel-consumption path) from one specified node in the network to another specified node; or we may need to find shortest paths from a specified node to all other nodes. Shortest paths between all pairs of nodes in a network are required in some problems. Sometimes, one wishes to find the shortest path from one given node to another given node that passes through certain specified intermediate nodes. In some application, one requires not only the shortest path but also the second and third shortest path. There are instances when the actual shortest path is not required, but only the shortest distance is required.

Next, we shall confine ourselves to two most important shortest-path problems; how to determine shortest distance (a short path) from a specified node to another specified node t, and how to determine shortest distances (all paths) from every node to every other in the network. Shortest path route problem deals with determining the connected arcs in transportation network that collectively comprise the shortest distance between a source and the destination. The shortest path problem involves a weighted, possibly directed graph described by the set of edges and vertices shortest path deals with two algorithms for finding the shortest route.

DIJKSTRA’S ALGORITHM

Dijkstra's algorithm, named after its inventor, has been influential in path computation research. It works by visiting nodes in the network starting with the object's start node and then iteratively examining the closest not-yet-examined node. It adds its successors to the set of nodes to be examined and thus divides the graph into two sets: S, the nodes whose shortest path to the start node is known and S’, the nodes whose shortest path to the start node is unknown. Initially, S’ contains all of the nodes. Nodes are then moved from S’ to S after examination and thus the node set, S-grows. At each step of the algorithm, the next node added to S is determined by a priority queue. The queue contains the nodes S’, prioritized by their distance label, which is the cost of the current shortest path to the start node. This distance is also known as the start distance. The node, u, at the top of the priority queue is then examined, added to S, and its out- links are relaxed. If the distance label of u plus the cost of the out- link (u, v) is less than the distance label for v, the estimated distance for node v is updated with this value. The algorithm then loops back and processes the next node at the top of the priority queue. The algorithm terminates when the goal is reached or the priority queue is empty. Dijkstra's algorithm can solve single source SP problems by computing the one-to-all shortest path trees from a source node to all other nodes. [2]

The pseudo-code of Dijkstra's algorithm is described below. Function Dijkstra (G, start)

1) d [start] = 0

2) S = ∅

3) S’ = V ∈G

4) while S’ ≠ ∅

5) do u = Min (S’)

6) S = S U {u}

7) for each link (u, v) outgoing from u

8) do if d[v] >d[u] + w (u, v) // Relax (u, v)

9) then d[v] = d[u] + w (u, v)

10) Previous[v] = u

FLOYD WARSHALL ALGORITHM

The Floyd –Warshall algorithm obtains a matrix of shortest path distances within 0{n3} computations. The algorithm is based on inductive arguments developed by an application of a dynamic programming technique. Let d^k (I, j) represent the length of the shortest path from node I to node j subject to the condition that this path uses the nodes 1, 2,……….. k – 1 as internal nodes. Clearly and +1 (i, j) for all node pairs i and j, when it terminates. Given d^k (i, j), the algorithm computes d^k+1(I, j) = min d^k {i, k,), d^k (k, j)}. The Floyd Warshall Algorithm remains of interest because it handles negative weight edges correctly [3].

Floyd Warshall algorithm or Floyd's algorithm is also recognized as the all pairs shortest path algorithm. It will calculate the shortest path between all possible pairs of vertices in a (possibly weighted) graph or digraph concurrently in time (where n is the number of vertices in the graph). In this problem we want the minimum routes (m. r.) between all the pairs of peaks. As an illustration of a path problem, the fire-brigade retains a map of the city marked with the locations of especially dangerous sites, such as chemical stores. They request to know the shortest route from the fire-station to each site. Note the "length" of a road might be either its physical length or the valued driving time on it, which are not certainly proportionate to each other. The Floyd algorithm solves this problem. This algorithm is an expansion of another algorithm, the Warshall algorithm, which was first defined for the solution of another problem: In a digraph G (whether there are costs or not, is of no importance) find whether there is a route from V(i) to V(j), for all pairs of (i, j), i <> j.

To solve this problem we find an array A. The elements of this array are A (i, j) = 1 if there is a route from i to j, otherwise A (i, j) = 0. Because the cost is not important we define the Adjoining Array as if all the costs were 1 that means C(i, j) = 1 if there is eij belonging to E and otherwise C(i, j) = 0. The requested array A is called transitive closure of the Adjoining Array. We notice that the elements of the A array are Boolean variables (0 or 1), which means that the operations AND and OR are valid. The Warshall algorithm initializes the A array at the value of C: A (i, j) = C(i, j), i, j =1,...,n. At this point the A array shows only the direct connections as existing routes. Then the algorithm goes through the A array n times, one time for every node k=1... n. For every node V (k) the main thinking is: Is there a route from V(i) to V(j), if it has already been found [that is A(i, j) = 1] or if a route is found through V(k),that is if the routes from V(i) to V(k) and from V(k) to V(j) [that is if A(i, k) =1 and A(k, j) =1].

If the BOOLEAN characteristics of the elements of A are taken under consideration, then the rule in the k pass is: A(i,j)=A(i,j) OR {A(i,k) AND A(k,j)}. We now come back to the m.r. problem for all pairs. This time we are talking about a graph, and the adjoining Array is defined by the costs C (i,j)=c(eij). The array will finally consist of all the costs of the minimum routes. During the k pass the following formula is valid: A(i,j) = min{A(i,j), A(i,k) + A(k,j) } Which means that if the route through V(k) is cheaper will be the winner. That gives us the Floyd algorithm. The complexity of the Floyd Algorithm is (in the worst case): O (n³). The weight of an edge in a fixed graph is often thought of as its length. The distance of a path is the sum of the lengths of all constituent edges . The outcome of the shortest paths between vertices in a graph is a vital class of problem.

SINGLE SOURCE SHORTEST PATHS IN A DIRECTED GRAPH

It fits out that it as easy to calculate the shortest paths from a single source to all other vertices as it is to discover the shortest path between any two vertices. Generally the source is taken to be v1. Dijkstra's algorithm solves this single-source shortest paths problem in O(|V|2) time. It meanings is broadening the set of vertices 'done' for which the shortest paths from the source are identified initially done, contain just the source v1. At any midway stage, the vertex not in the set done that is closest to the source is found and added to done. This permits our knowledge of the shortest paths to the residual vertices in V - done to be updated. This is repeated until done for all contain vertices. The algorithm monitors what is known as a greedy strategy. It adds vertices to done as cheaply as possible. The approach is often a good heuristic; in this problem it also gives a correct algorithm. As agreed, the algorithm calculates the lengths of the shortest paths from the source to each other vertex. If it is necessary to find the paths themselves, note that the algorithm traces a rooted tree with the source as the root. Since the vector of path distances is updated, if P (j) is minimized by the 'min' then 'closest' can be associated with j in another vector. This reaches agreement with the paths to be improved, in a reverse direction.

Floyd's algorithm computes the costs of the shortest path between each pair of vertices in O (|V|3) time. It contains of three nested loops. The unchangeable of the outer loop is the key to the algorithm. At the start of iteration, P holds the optimal path length from vi to vj, for each i and j, bearing in mind only paths that go direct or via vertices vn for n < k. This is definitely true originally when k=1 and P holds only direct paths. At each iteration the next value of k is considered. There may now be a improved path possible from vi to vj via this new vk, but note that it will visit vk at most once. This means it is adequate to reflect paths from vi to vk possibly via {v1, ..., vk-1} and then on from vk to vj also possibly via {v1, ..., vk-1}. Thus the Invariant is maintained. Finally P holds optimal path lengths for unrestricted paths.

In unpretentious terms, the Floyd Warshall algorithm finds a matrix of shortest distances inside 0{n³} calculations. The algorithm is based on inductive opinions developed by an submission of a dynamic programming technique. Let d^k(i,j) denote the distances of the shortest path from i to node j subject to the form that this path uses the nodes 1,2,….k-1 as internal nodes. Clearly, dⁿ⁺¹(i,j) denotes the actual shortest path distance from node i to j. The algorithm first calculates d¹(i,j) for all node pairs i and j. using d¹(i,j) it then computes d²(i,j) for all node pairs i and j. It duplicates this procedure until it find dⁿ⁺¹(i,j) for all node pairs i and j, when it ends. Given d^k(i, j), the algorithm computes d^k+1(i, j)= min{d^k(i, k), d^k (k , j )}. The Floyd Warshall algorithm remains of interest because it handles negative weight edges correctly [3] and [4].

3. Chapter Three

CASE STUDY: - KWAME NKRUMAH UNIVERSITY OF SCIENCE AND TECHNOLOGY, KNUST.

Sixty seven years ago, this golden University was given birth to in Kumasi, the cultural capital of Ghana. Kwame Nkrumah University of Science and Technology sits on the seam of gold: 60 km from the campus is Obuasi, one of Africa's richest gold mines, belonging to the Ashanti Goldfields Corporation. This institution is best known as Africa's pride for training her pioneer engineers, scientists, architects, planners, doctors, agriculturists, fine artists and pharmacists and of course statesmen: His Excellency Dr. Kofi Annan, Secretary General of United Nations is our favourite alumnus. The University of Science and Technology presided the Kumasi College of Technology which was recognized by a Government Ordinance on 6th October, 1961. It, nevertheless, opened officially on 22nd January, 1952 with 200 Teacher Training students transferred from Achimota, to form the center of the new College. In October, 1952, the School of Engineering and the Department of Commerce were set up and the first students were admitted. From 1952 to 1955, the School of Engineering prepared students for professional qualifications only. In 1955, the School embarked on courses leading to the University Of London Bachelor Of Engineering External Degree Examinations. A Pharmacy Department was set up in January, 1953, with the handover of the former School of Pharmacy from Korle-Bu Hospital, Accra, to the College. The Department completed a two-year all-inclusive course in Pharmacy foremost to the award of the Pharmacy Board Certificate. A Department of Agriculture was opened in the same year to provide a number of courses of varying period, from a few terms to three years, for the Ministry of Agriculture. A Department of General Studies was also instituted to prepare students for the Higher School Certificate Examinations in both Science and Arts subjects and to give tuition in such subjects as were demanded by the other departments. Once recognized, the College began to grow and in 1957, the School of Architecture, Town Planning and Building was initiated and its first students were admitted in January, 1958, for professional courses in Architecture, Town Planning and Building. As the College expanded, it was decided to make the Kumasi College of Technology a purely science and technology establishment. In search of this policy, the Teacher Training College, with the exclusion of the Art School, was reassigned in January, 1958, to the Winneba Training College, and in 1959 the Commerce Department was relocated to Achimota to form the basis of the present School of administration of the University of Ghana, Legon. In December, 1960, the Government of Ghana selected a University Commission to counsel it on the forthcoming progress of University Education Ghana, in association with the suggestion to transform the University College of Ghana and the Kumasi College of Technology into an self-governing University of Ghana. Following the report of the commission, which came out early 1961, Government decided to start two independent Universities in Kumasi at Legon near Accra. Kumasi College of Technology was consequently reformed into a complete University Kwame Nkrumah University of Science Technology via an Act of Parliament on 22nd August, 1961. The University name was reformed to University of Science and Technology after the Mutiny of 24th February 1966. The University of Science and Technology was formally establish in office on Wednesday, 20th November 1961. However, by another act of Parliament, Act 559 of 1998, the University has been retitled Kwame Nkrumah University of Science and Technology, Kumasi.

HOW DATA WERE COLLECTED

Since this project is essentially determining the shortest distance from a point, junction or city to the other, then it becomes obligatory that we know some junctions and distances between them. Most of the data (map, measurements, names of junctions and some settlements, rivers etc.) were collected at the Geography Drawing room. The Geography Drawing Room can be located at the Department of Land Economy. Though this department could not supply us all the required information, efforts were later made to obtain them. This section which hectic times took almost two (2) days to a perfect completion, provided below is the map of KNUST.

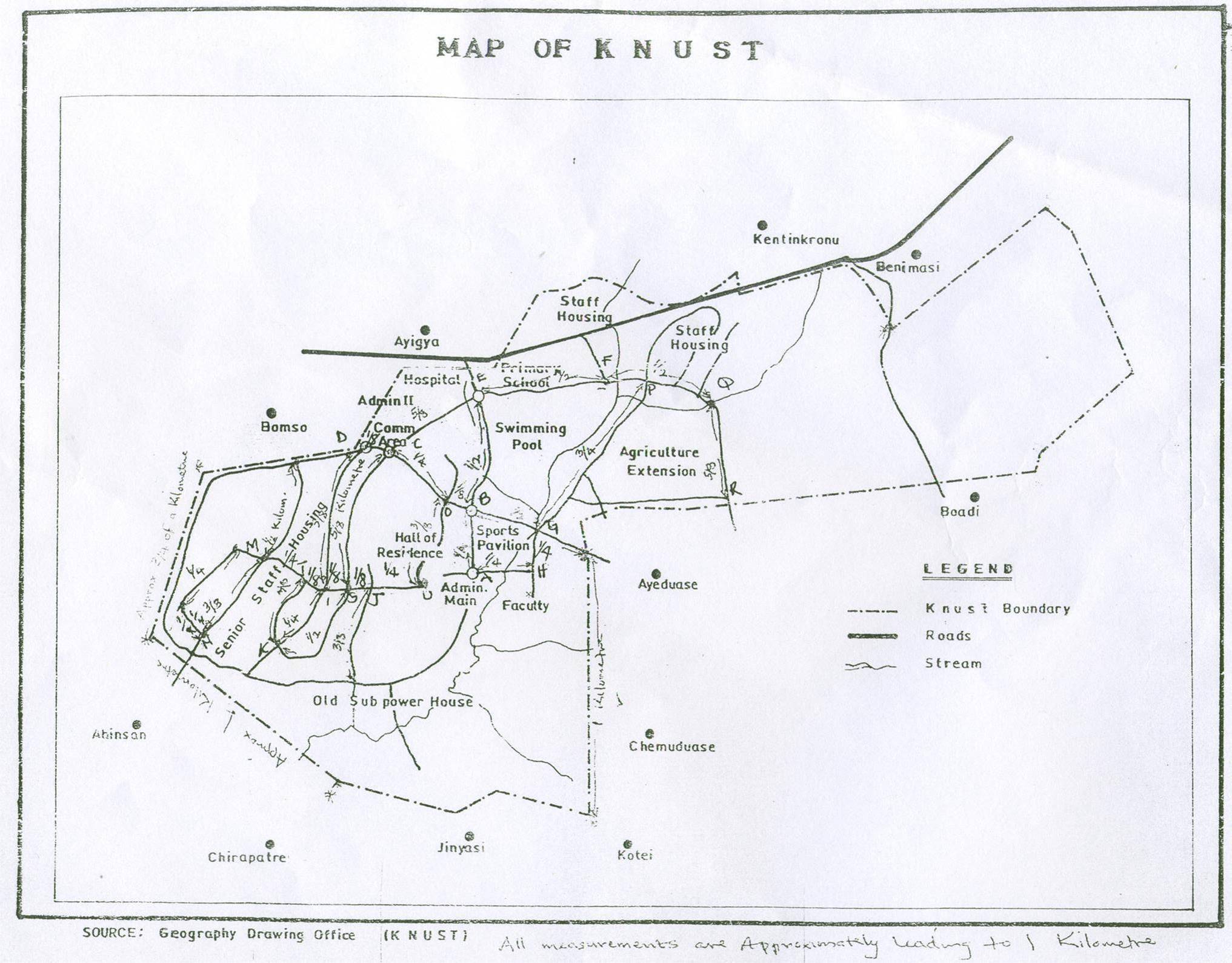Figure 2. Map of Knust Alphabetical Labeling of the Junctions

NAMES OF LETTERS ALLOCATED RANDOMLY TO SOME POINTS (NODES) ON THE MAP

A~Administration RA

B~Unity RA

C~Universty Printing Press RA

D~Bomso Gate RA

E~Main Entrance RA

F~Botanical Garden J

G~Agric Road J

H~Taxi Road J

I~Okodee Road J

J~Asuogya Road J

K~Akuroso J

L~Old Sub Power House J

M~New Ridge Road J

N~Ring Ring J

O~Institute Of Land Management & Development J

P~Mangoasi J

Q~Gaza J

R~mango Road J

S~Senior Staff Club J

T~Bomso Crescent Road J

U~Great Hall J

RA~Runabout

J~Junction

4. Chapter Four

SOLUTION FROM FLOYD’S ALGORITHM

The map on page 3 shows twenty-one campsites, A, B, C, D, E, F, G, H, I, J, K, L, M,

N, O, P, Q, R, S, T and U in K.N.U.S.T campus, together with paths connecting them.

The numbers by paths show lengths, in kilometers, of sections of path.

Using the Floyd’s algorithm the shortest distance between each of the junctions can be calculated as follows;

From the above calculations one would comprehend that there are two mutual solutions which are 0.375 and ∞. It is also obvious from this point that 0.375 is the minimum. Hence the shortest distance amongst AC is 0.375. Using the same technique other shortest distances have been designed in table 2 below

SOLUTION FROM FLOYD’S ALGORITHM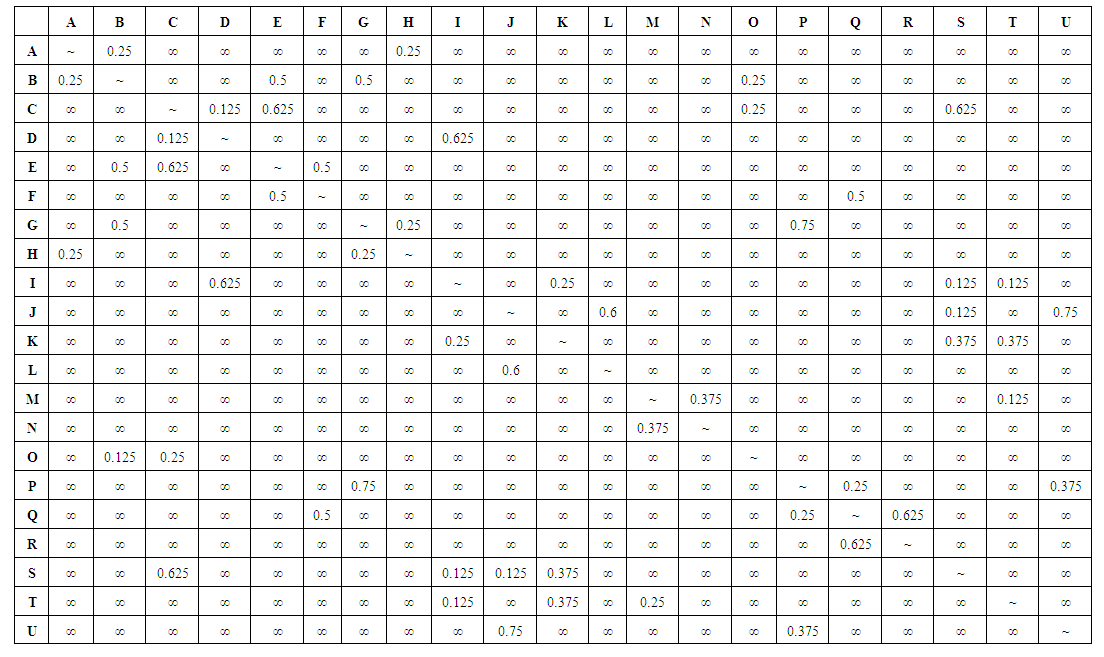

The table below shows each distance between each of the junctions on the map

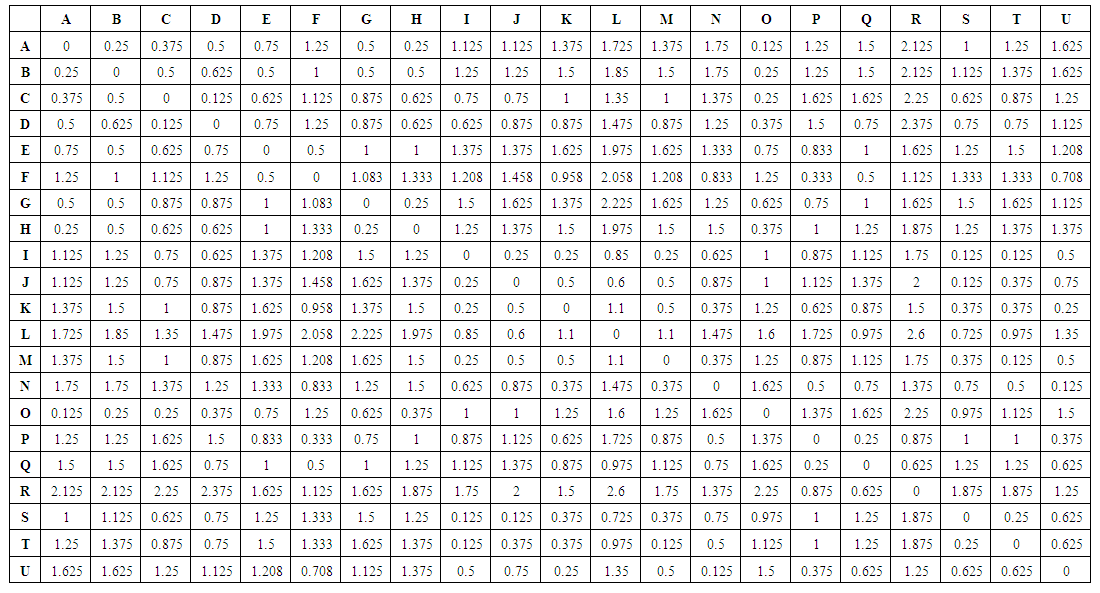Using the same procedure other shortest distances have been calculated in table 2 below

5. Chapter Five

CONCLUSIONS AND RECOMMENDATIONS

Floyd's algorithm works by viewing for all non-direct paths amongst two vertices that have a less-expensive total cost than the best way yet found to move between said vertices. If such a path is found, it becomes the value against which future indirect paths between these vertices are tested. In the end, each element of the matrix signifies the lowest-cost traversal between the vertices it's row and column represent. Recollect that if the graph is directed, so is the answer in (i, j) of the matrix; moreover, (i, j) may not be equal to (j, i) in a di-graph. It is important to note, however Floyd's algorithm is as good as or better than Dijkstra’s algorithm.

In this work there introduced a novel approach for calculating the shortest path in networks with cycles. The proposed approach, the Rectangular algorithm, improves on the Floyd–Warshall algorithm, one of the best available algorithms for treating this problem, in a number of ways. The Floyd Warshall algorithm and the Rectangular algorithm have exactly the Same performance in deriving these matrices. For the stages j ≥1, however, the Rectangular algorithm derives the associated matrices much more quickly due to the reduced amount of calculation. This has been explained graphically using simulated data.

In conclusion the shortest distance from any area on campus to another can be calculated, let us have a look at the case of an emergence call, requesting an fire service to rush from station to any of the hall of residence in knust campus. The shortest distance can easily be known using this project, because a link on a real road network in the city tends to posse different levels of congestion during different time period of a day and because a Patient’s location cannot be expected to be known in advance, it is practically impossible to determine the fastest route before a call is received. The collection, transport and disposal of solid waste, which is a extremely noticeable and important municipal service, involves a large expenditure but receives, scant responsiveness. This difficult is even more essential for big cities in developing countries due to the hot weather once again the shortest distance can also be calculated using this project.