-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2019; 9(1): 6-12
doi:10.5923/j.am.20190901.02

The Set Ordering Method for Scoring the Outcomes of 1-2-4 Multistage Model of Computerized Adaptive Testing
Simon Razmadze
Georgian Computer Society, Tbilisi, Georgia
Correspondence to: Simon Razmadze , Georgian Computer Society, Tbilisi, Georgia.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The paper presented considers the ordering method of outcome set for multi-stage testing (MST) of 1-2-4 model. The ordering method of outcome set is used for the estimation of results of computerized adaptive testing (CAT). This method is not tied to a specific testing procedure. Acknowledgment of this is its usage for the 1-2-4 model, which is described in the paper. To sort the set of testing outcomes the function-criteria described in the initial article are used here and a comparative analysis of obtained results is performed. The ordered outcome set is estimated by a hundred-point system according to the normal distribution.
Keywords: Computerized adaptive testing, Stradaptive testing, Multistage adaptive testing, Evaluation algorithm, Ordering of a set
Cite this paper: Simon Razmadze , The Set Ordering Method for Scoring the Outcomes of 1-2-4 Multistage Model of Computerized Adaptive Testing, Applied Mathematics, Vol. 9 No. 1, 2019, pp. 6-12. doi: 10.5923/j.am.20190901.02.
Article Outline
1. Introduction
- Computerized adaptive testing implies the test adaptation to the level of knowledge of the test. During the testing process the system analyzes the answers and uses them to choose each following question based on the best correspondence to the level of examinee so that the questions gradually become complicated for a well-prepared examinee and simpler for a poorly prepared person. The process of test adaptation for an individual user is mentioned.This means that the tests must be pre-calibrated according to their level of difficulty.The modern computerized adaptive testing (CAT) is based on item response theory (IRT). IRT is a family of mathematical models that describe how people interact with test items [1]. According to this theory test items are described by their characteristics of difficulty and discrimination. Discrimination is independent of difficulty and shows how the probability of a positive response is distributed between different levels of examination. In addition, they can have a so-called “pseudo-guessing” parameter that reflects the probability that an examinee with a very low trait level will correctly answer an item solely by guessing [2]. The combination of these three parameters allows us to evaluate the knowledge of an examinee via the Maximum Likelihood Estimation (MLE) method. The MLE method is much more flexible than the so-called The “Number Correct” assessment, which implies the number of correct answers from the questions asked (perhaps, considering question weight). For example, number-correct scoring of a 10-item conventional test can result in at most 11 scores (0 to 10); MLE for the same test can result in 210=1024. MLE also provides an individualized standard error of measurement (SEM) for each examinee.Despite the above and other advantages, the MLE method requires extensive preliminary work to determine with appropriate accuracy the difficulty, discrimination, and guessing parameter for each issue of the test. The most common method of determining these parameters is the preliminary testing. To get real results via the preliminary testing, it is necessary to examine hundreds and thousands of users, which is not easy.In general, to obtain the advantages of the Item Response Theory (IRT), the tests should be designed, constructed, analyzed and interpreted within the framework of the given theory. Particularly, IRT implies that the ability of the particular examinee is known in advance, and based on these data, the parameters of the characteristic curve of items (difficulty, discrimination, guessing parameter) are determined [2].In the considered model a set of items of the test is divided into several parts, depending on complexity. Subsequently, there is no other information available about the items on a test. In other words, the difficulty, discrimination and parameter of guessing for each item separately are not available. The model under discussion does not present the preliminary estimate parameter θ of an examinee’s abilities. True, the lack of information decreases the accuracy of the result, but the big advantage of a simple model is that its practical application is easy.We will try to create a test assessment system that makes it easy for the test creator to use a computer-adaptive method for creating one’s own test. For this purpose, let us not discuss IRT but another traditional approach to testing—Stradaptive Testing. The term “Stradaptive” is derived from the “Stratified Adaptive”, and it belongs to D.J. Weiss [3, 4].Stradaptive testing considers different strategies of the leveling, which were fundamentally discussed and studied earlier. These strategies are:Ÿ Two-stage approach [3, 4, 5];Ÿ Multi-Stage Approach:ο Fixed Branching Models:§ Pyramidal Strategy [5];§ Flexilevel [6, 7, 8];§ Stradaptive Testing [9, 10, 11];ο Variable Branching Models:§ Bayesian [10, 12];§ Maximum likelihood approach [10].In the given paper we consider multistage testing.
2. Multistage Adaptive Testing
- “Recently, multistage testing (MST) has been adopted by several important large-scale testing programs and become popular among practitioners and researchers” [13, p. 104]. “MST is a balanced compromise between linear test forms (i.e., paper-and-pencil testing and computer based testing) and traditional item-level computer-adaptive testing (CAT)” [14, p. ii]. The multistage adaptive test represents structured adaptive test, which uses pre-designed subtests as the main unit of testing control. “In contrast to item-level CAT designs, which result in different test forms for each test taker, MST designs use a modularized configuration of pre-designed subtests and embedded score-routing schemes to prepackage validated test forms” [15, p. 171].The “stage” in multistage testing is an administrative division of the test that facilitates the adapting of the test to the examinee. Each examinee is administered modules for a minimum of two stages, where the exact number of stages is a test design decision affected by the extent of desired content coverage and measurement precision. In each stage, an examinee receives a module that is targeted in difficulty at the examinee’s provisional ability estimated, computed from the latter’s performance on modules administered during the previous stage(s). Within a stage, there are typically two or more modules that vary from one another based on average difficulty. Because the modules vary this way, the particular sequence of item sets that any examinee is presented with is adaptively chosen based on the examinee’s temporary assessment. After an examinee finishes each item set, his or her ability estimate is updated to reflect the new measurement information obtained about his ability. The next module is chosen to provide an optimal level of measurement information for a person at that computed proficiency level. High-performing examinees receive modules of higher average difficulty, while less able examinees are presented with modules that are comparatively easier [16].Thus, traditional CAT selects items for a test adaptively, while a multistage testing (MST) is an analogous approach that uses sets of items (modules, testlets) as the “building blocks” for a test. In MST terminology, these sets of items have come to be termed modules [17, 18, 19] or testlets [20, 21] and can be characterized as short versions of linear test forms where some specified number of individual items are administered together to meet particular test specifications and provide a certain proportion of the total test information.
3. Ordering Method of Outcome Set
- The initial article [22] considers an original method of CAT result estimation for multistage testing strategy.In contrast to the classical item response theory (IRT) concepts [1, 23, 2], Rasch’s model [24] or non-IRT (i.e. the Measurement Decision Theory) of CAT [25], the model under discussion, does not present the preliminary estimate parameter θ of an examinee’s abilities and the items of the same level have the same difficulty.The method considers all possible variants of results, which is named an outcome set. The outcome set represents a non-typical unity of different dimensional elements. At [22] article comparison criteria for these elements are defined, and principles of ordering of the set are described. The article shows how to receive the final score after ordering the outcome set. The ordered criteria of outcomes set may not be singular; this is confirmed by a comparative review of two examples presented in this work.In multistage testing, to build a panel using modules, an author of a test uses a linear programming or heuristic methods. Apart from this, Fisher’s Maximum Information Method is used for obtaining the classification cut-points for the optimization of the information of a module [14]. All the above mentioned requires specific knowledge. Our model does not have such limitations for a test author because such specific work is performed by an “automatic system of testing” compiler, while the author of a test has only to divide the testing items into several levels according to difficulty. This procedure should not be complicated because we assume that the author of this test is a professional in the field for which the appropriate test is created.To express the ordering method of outcomes set, a specific procedure for testing is used in [22] article. This procedure has an illustrative purpose for the evaluation method. The method described can be used for other similar strategies as well as for multistage testing, one of the models considered in this paper.Thus, the paper presented is devoted to the realization of an ordering method of the outcome set, in particular on the example of a three-stage 1-2-4 model.
4. The Three-stage 1-2-4 Adaptive Model
4.1. The Scheme of 1-2-4 Model
- Now let us consider the usage of the ordering of testing result scores in case of multistage adaptive testing. For this purpose, we will discuss the three-stage 1-2-4 model, which is presented in the scheme (Figure 1) [14].The number indicated in the rectangle of the module corresponds to the stage; the letters correspond to comparative difficulty (H: high; M: medium; L: low; HH: higher than H; LL: lower than L).
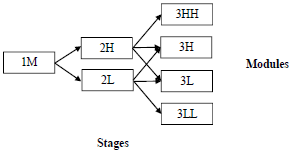 | Figure 1. The 1-2-4 MST model |
|
|
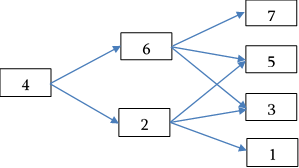 | Figure 2. The 1-2-4 MST model with weights |
4.2. Outcome of 1-2-4 Model
- In the first row of Table 2, all modules are numbered from 1 to 7. We will be using the given numbering for defining the test outcome. Taking into account the complexity levels of the modules, the outcome is expressed as a seven-dimensional vector:
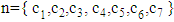 , where
, where 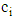 represents the number of correct answers of i module,
represents the number of correct answers of i module, 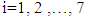 . Due to the fact each testee performs only one item on each stage, there can be only 3 components out of a given 7 that are different from 0 in each test outcome. In addition, each
. Due to the fact each testee performs only one item on each stage, there can be only 3 components out of a given 7 that are different from 0 in each test outcome. In addition, each 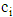 component,
component, 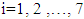 , has a weight, predefined according to Table 2.In [22, p. 1656] article the outcome was defined as a vector drawn from the corresponding numbers of the levels of items obtained during the testing process. In this case, by definition, the outcome vector consists of the components that correspond to the number of correct answers in each module. This is more convenient for using the set ordering method for multistage adaptive tests.Let us look at how many items there are per module. According to the module given by [14], the examinee is given 21 items that can be distributed among the stages differently:
, has a weight, predefined according to Table 2.In [22, p. 1656] article the outcome was defined as a vector drawn from the corresponding numbers of the levels of items obtained during the testing process. In this case, by definition, the outcome vector consists of the components that correspond to the number of correct answers in each module. This is more convenient for using the set ordering method for multistage adaptive tests.Let us look at how many items there are per module. According to the module given by [14], the examinee is given 21 items that can be distributed among the stages differently:
|
4.3. Outcome Route
- Modules of the first and second stages have classification cut-points that define the route of the testing outcome; in other words, choosing the second and third stage modules. Classification cut-point is the amount of correct answers within the module that defines the branching – next stage module. Despite where the classification cut-points are chosen the total amount of the testing outcomes is constant and N = 512. An example discussed in this article on the first stage of 1M module cut-point equals to 4. This means, that in case of less than 4 correct answers (0, 1, 2 or 3) an examinee will be given the easier 2L module of the second stage, and in case of 4 or more correct answers (4, 5, 6 or 7) – the more difficult 2H module of the second stage.The second stage modules have two classification cut-points: Ÿ The classification cut-points of the module 2L are 2 and 5 – if the number of correct answers are less than 2 (0 or 1), the examinee is given the easiest module 3LL, if the number of correct answers are between 2 and 5 (2, 3 or 4) – the third stage easy 3L module and if the number of correct answers are 5 or more (5, 6 or 7) – the third stage difficult 3H module;Ÿ The classification cut points of the module 2H are 3 and 6 – if the number of correct answers is less than 3 (0, 1 or 2), the examinee is given the third stage easy 3L module, in case of the number is between 3 and 6 (3, 4 or 5) – the third stage difficult 3H module and in case there are 6 or 7 correct answers – the third stage most difficult 3HH module.
5. The Set Ordering Method for Scoring the Outcomes of the 1-2-4 Model
5.1. Ordering According to the S(n) Criterion
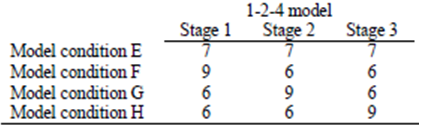
- Let us discuss the first criterion from the initial article [22, p. 1658, Formula (4)]:
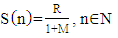 | (1) |
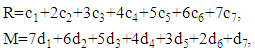 where
where 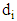 is a number of mistakes in i module,
is a number of mistakes in i module, 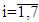 .The Formula (1), which should be used for outcome estimation, is now used in the seven-module case. The structure of outcome set of the three-stage model discussed in this article is different from the one discussed in the initial article by Razmadze et al [22, p. 1656]. This means that the domain of a function
.The Formula (1), which should be used for outcome estimation, is now used in the seven-module case. The structure of outcome set of the three-stage model discussed in this article is different from the one discussed in the initial article by Razmadze et al [22, p. 1656]. This means that the domain of a function 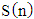 is different. Despite this,
is different. Despite this, 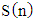 function will provide complete ordering of set N in a given case too.
function will provide complete ordering of set N in a given case too.
|
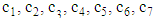 values are given in the columns B, C, D, E, F, G, H, respectively. The values calculated using Formula (1) are shown in column M. The data is sorted according to M column decreasing order. The table shows the first 10 (a) and last 10 (b) testing outcomes’ estimation results.
values are given in the columns B, C, D, E, F, G, H, respectively. The values calculated using Formula (1) are shown in column M. The data is sorted according to M column decreasing order. The table shows the first 10 (a) and last 10 (b) testing outcomes’ estimation results. 5.2. Ordering According to the F(n) Criterion
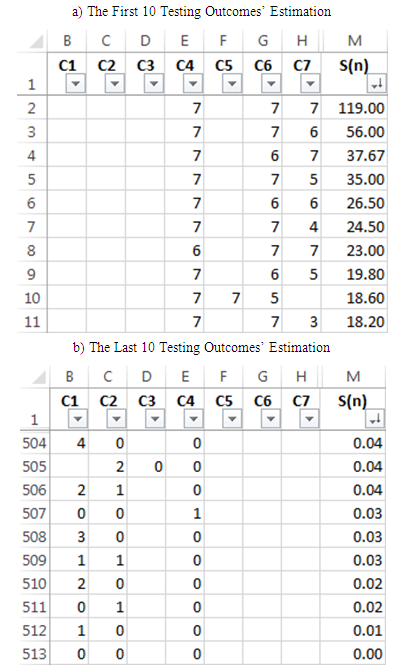
- Let us discuss the second criterion from the initial article [22, p. 1658, Formula (9)]:
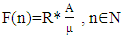 | (2) |
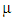 – the number of mistakes.The corresponding formulas for calculating R and A are given in the initial article by Razmadze et al. [22, p. 1657], Formulas (1) and (3)). Based on these formulas, in the case of the 1-2-4 MST model, we will obtain the following:
– the number of mistakes.The corresponding formulas for calculating R and A are given in the initial article by Razmadze et al. [22, p. 1657], Formulas (1) and (3)). Based on these formulas, in the case of the 1-2-4 MST model, we will obtain the following: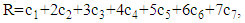
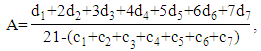 where
where 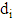 is a number of mistakes in i module,
is a number of mistakes in i module, 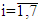 .
. 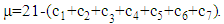 The Formula (2), which should be used for outcome estimation, is now used in the seven-module case. The structure of the outcome set of the three-stage model discussed in this article is different from the one discussed in the initial article by Razmadze et al [22, p. 1656]. This means that the domain of a function
The Formula (2), which should be used for outcome estimation, is now used in the seven-module case. The structure of the outcome set of the three-stage model discussed in this article is different from the one discussed in the initial article by Razmadze et al [22, p. 1656]. This means that the domain of a function 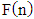 is different. Although, it is easy to check that despite this,
is different. Although, it is easy to check that despite this, 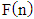 function will provide a complete ordering of set N in the given case too.The results obtained by using
function will provide a complete ordering of set N in the given case too.The results obtained by using 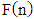 criterion are shown in Table 5, where
criterion are shown in Table 5, where 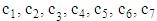 values are given in the columns B, C, D, E, F, G, H, respectively. The values calculated using Formula (2) are shown in column N. The data is sorted according to N Column decreasing order. Table 5 shows the first 10 (a) and the last 10 (b) testing outcomes’ estimation results.
values are given in the columns B, C, D, E, F, G, H, respectively. The values calculated using Formula (2) are shown in column N. The data is sorted according to N Column decreasing order. Table 5 shows the first 10 (a) and the last 10 (b) testing outcomes’ estimation results.
|
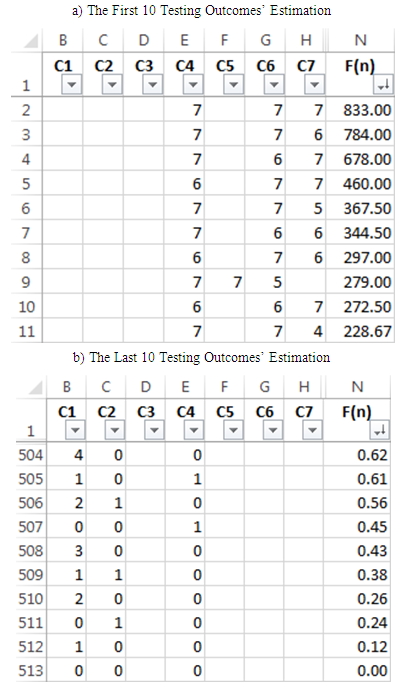
5.3. The Final Score of Outcome
- Now let us transform the points obtained in Tables 4 and 5 into integer numbers [0; 100] segment. While ordering the data obtained by the first and the second criteria in [22, pp. 1659, 1660] article, the point correction was performed. In case of the first criterion - the first 90 points and in case of the second criterion - the first 30 points. This felt somewhat artificial. Now let us act differently. The criteria
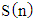 and
and 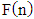 , used in Tables 4 and 5, have fulfilled their mission and ordered the set of the testing outcomes N. The resulting points do not have essential importance. They can be substituted by any decreasing sequence of 512 numbers. The decreasing order ensures to keep the ordering of the testing outcomes so that the better testing result corresponds to the higher point.
, used in Tables 4 and 5, have fulfilled their mission and ordered the set of the testing outcomes N. The resulting points do not have essential importance. They can be substituted by any decreasing sequence of 512 numbers. The decreasing order ensures to keep the ordering of the testing outcomes so that the better testing result corresponds to the higher point.
|
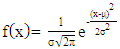 | (3) |
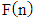 criterion, where
criterion, where 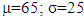 .Table 6 shows the first 10 (a) and the last 10 (b) testing outcomes’ scores. The whole table graphically looks as follows (Figure 3):
.Table 6 shows the first 10 (a) and the last 10 (b) testing outcomes’ scores. The whole table graphically looks as follows (Figure 3): 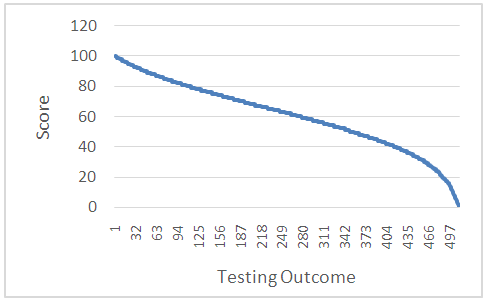 | Figure 3. Graph of 1-2-4 MST model testing outcomes’ score’s normal distribution |
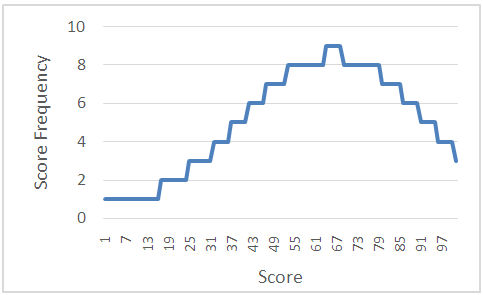 | Figure 4. Normal distribution of the testing outcome points |
6. Conclusions
- The ordering method of the outcome set can be used in case of different testing procedures. The obvious example of this is the realization of the method for multistage adaptive testing’s (MST) 1-2-4 model, which is described in the presented paper. The author of a test has no direct contact with this method and its specific nuances because the realization of the method is a one-time procedure, carried out during the computerized adaptive testing portal formation.The method does not require a detailed calibration of the item pool or preliminary testing of examinees to create a calibration sample. The ordering method of outcome set is oriented on the test author; it helps him avoid the problem of preliminary adaptation of test items for the examinee’s knowledge level and simplifies the workload at maximum. Preliminary work for the test author might only include the division of test items into several difficulty levels based on expert assessment.In the situation where there is a lack of information about test item's and examinee’s level, the method maximally uses the existing information for an examinee estimation: it takes into account all the answers to the questions provided to the examinee and the set of received answers is compared to all the possible variants and placed on corresponding level in the estimation hierarchy.The paper presents the usage of the ordering method of outcomes set for multistage adaptive testing (MST) model as a sample. The method can be used for different modern testing models, but it is the subject of further research.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML