I. M. Esuabana1, U. A. Abasiekwere2
1Department of Mathematics, University of Calabar, Calabar, Cross River State, Nigeria
2Department of Mathematics and Statistics, University of Uyo, Uyo, Akwa Ibom State, Nigeria
Correspondence to: I. M. Esuabana, Department of Mathematics, University of Calabar, Calabar, Cross River State, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
One of the most recent mathematical concepts, the regularization methods for solving integral equations, has brought in yet another dimension into the existing problems and has helped to usher in a new body of knowledge for further consideration. Indeed, new inputs have placed other numerical methods for solving integral equations in the fastest lane, since a number of methods were analysed with respect to accuracy, convergence and stability properties. Most of the work was done on the assumptions that the kernel 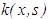 and the right-hand side
and the right-hand side 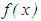 are known without error and that the approximating equation can be exact, whereas, as is often the case, these may not be true. Consequently, the effect can be observed in the study of regularization methods for solving Volterra type integral equations of the first kind. Classical regularization methods tend to destroy the non-anticipatory (or causal) nature of the original Volterra problem because such methods typically rely on the computation of the Volterra adjoint operator. In this paper, we highlight the general concept of the regularization method of solution for Volterra integral equation of the first kind without destroying the Volterra structure.
are known without error and that the approximating equation can be exact, whereas, as is often the case, these may not be true. Consequently, the effect can be observed in the study of regularization methods for solving Volterra type integral equations of the first kind. Classical regularization methods tend to destroy the non-anticipatory (or causal) nature of the original Volterra problem because such methods typically rely on the computation of the Volterra adjoint operator. In this paper, we highlight the general concept of the regularization method of solution for Volterra integral equation of the first kind without destroying the Volterra structure.
Keywords:
Volterra Integral Equation, Regularization method, Ill-posed
Cite this paper: I. M. Esuabana, U. A. Abasiekwere, A Survey of Regularization Methods of Solution of Volterra Integral Equations of the First Kind, Applied Mathematics, Vol. 8 No. 3, 2018, pp. 33-41. doi: 10.5923/j.am.20180803.01.
1. Introduction
The theory of integral equations is interesting, not only in itself but also in the absolute importance of its results in the analysis of numerical methods of solution of various equations. Besides the concept of existence and uniqueness with respect to differential equations, the theory is concerned, in particular, with questions of regularity and stability of their solutions.In the last two and a half decades, there has been a tremendous increase in the applications of first kind integral equations of Volterra type. Among the areas where the applications of such class of equations abound in the natural sciences is the problem of restoration of incoming signals at the entrance of measuring instruments and observatory systems which, in view of their physical nature, allow some distortions of the observed and registered data [1].An integral equation is a functional equation in which the unknown function appears under one or several integral signs. In an integral equation of Volterra type for instance, the integrals containing the unknown function are characterized by a variable upper limit of integration. To be more precise, an integral equation of the form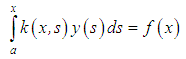 | (1) |
is called a linear Volterra integral equation of the first kind, or that of the form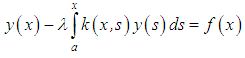 | (2) |
is called a linear Volterra integral equation of the second kind. Here, 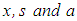 are real numbers,
are real numbers, 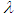 is a parameter,
is a parameter, 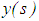 is an unknown function, while
is an unknown function, while 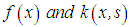 are given functions which are square integrable on
are given functions which are square integrable on 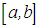 and in the domain
and in the domain 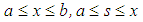 respectively. The function
respectively. The function 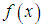 is called the free term, while the function
is called the free term, while the function 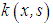 is called the kernel.One distinguishing feature associated with this class of equations is the uncertainty surrounding their nature and this is reflected in the difficulties encountered when attempting to find their solutions using one or the other of the existing numerical methods [2]. On one hand, Volterra integral equations of the first kind appear to be special cases of Fredholm integral equations of the first kind and are consequently classified among the lists of ill-conditioned problems solvable by the classical regularization means. On the other hand, given a set of limitations (for example, given that their kernels and right-hand sides are “good” and “smooth”) Volterra integral equations of the first kind belong to the class of well-posed problems and hence can be solved through any direct method based on the discretization of the unknown solutions. Both approaches seem to be a little on the extreme. The use of discretization process transforms Volterra integral equations of the first kind into another problem (often systems of linear equations and may be solved by the well-known singular value decomposition) that can lead to solutions which may or may not deviate strongly from the (minimum norm) solution of the original equation [3]. A complete regularization (with its accompanying difficulties and unresolved questions) turns out to be a too complicated approach as it is observed that the methods for Volterra equations of the first kind are not nearly as ill-posed as methods for Fredholm integral equations of the first kind.In this study, we investigate the regularization methods with a view to identifying the properties and types that can be used in solving Volterra type equations of the first kind, but without destroying the Volterra structure. The methods in view are perhaps the discrete regularization methods. The discrete approximation methods provide another approach to regularize the original problem. In this case, the regularization parameter is the discretization parameter (or step size) and coordination between this parameter and the amount of noise
is called the kernel.One distinguishing feature associated with this class of equations is the uncertainty surrounding their nature and this is reflected in the difficulties encountered when attempting to find their solutions using one or the other of the existing numerical methods [2]. On one hand, Volterra integral equations of the first kind appear to be special cases of Fredholm integral equations of the first kind and are consequently classified among the lists of ill-conditioned problems solvable by the classical regularization means. On the other hand, given a set of limitations (for example, given that their kernels and right-hand sides are “good” and “smooth”) Volterra integral equations of the first kind belong to the class of well-posed problems and hence can be solved through any direct method based on the discretization of the unknown solutions. Both approaches seem to be a little on the extreme. The use of discretization process transforms Volterra integral equations of the first kind into another problem (often systems of linear equations and may be solved by the well-known singular value decomposition) that can lead to solutions which may or may not deviate strongly from the (minimum norm) solution of the original equation [3]. A complete regularization (with its accompanying difficulties and unresolved questions) turns out to be a too complicated approach as it is observed that the methods for Volterra equations of the first kind are not nearly as ill-posed as methods for Fredholm integral equations of the first kind.In this study, we investigate the regularization methods with a view to identifying the properties and types that can be used in solving Volterra type equations of the first kind, but without destroying the Volterra structure. The methods in view are perhaps the discrete regularization methods. The discrete approximation methods provide another approach to regularize the original problem. In this case, the regularization parameter is the discretization parameter (or step size) and coordination between this parameter and the amount of noise 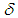 in the problem is required to obtain good approximations in the presence of noise.
in the problem is required to obtain good approximations in the presence of noise.
2. The Concept of a Regularizing Operator
We are already aware of the fact that the problem of solving Volterra integral equations of the first kind in some spaces, for example, in the triple (C,V,C) is, to a certain extent, ill-posed. Even in those spaces where the problems are well-conditioned, for example, in the space (C,V,C(1)), we still encounter significant difficulties, leading to some slight instabilities in the results during actualization. Consequently, to improve on the stability of the solutions which implies the accuracy of the desired results, we go out for the most stable methods. Among such methods are the regularization methods.Methods for construction of approximate solutions of ill-posed problems that are stable with respect to small perturbations of the initial data are referred to as regularization methods. The approach is based on what is called the fundamental concept of a regularizing operator [4]. In what follows, we examine the concept in detail.Suppose the operator A in the equation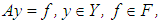 | (3) |
where Y and F are some metric spaces and A is a continuous operator mapping Y into F, is such that its inverse 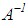 is also continuous in the set
is also continuous in the set 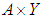 and the set Y of possible solutions, is not compact.If the right–hand member of the equation is an element
and the set Y of possible solutions, is not compact.If the right–hand member of the equation is an element 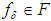 that differs from the exact right–hand member
that differs from the exact right–hand member 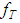 by no more than
by no more than 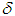 , that is, if
, that is, if 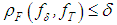 , it is obvious that the approximate solutions
, it is obvious that the approximate solutions 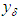 of equation (3) cannot be defined as the exact solution of this equation with approximate right–hand member
of equation (3) cannot be defined as the exact solution of this equation with approximate right–hand member 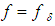 , that is, according to the formula
, that is, according to the formula 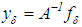 .The numerical parameter
.The numerical parameter 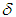 characterizes the error in the right–hand member of equation (3). Therefore, it is natural to define
characterizes the error in the right–hand member of equation (3). Therefore, it is natural to define 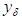 with the aid of an operator depending on a parameter having a value chosen in accordance with the error
with the aid of an operator depending on a parameter having a value chosen in accordance with the error 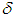 in the initial data
in the initial data 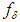 . Specifically, as
. Specifically, as 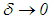 , that is, as the right–hand member
, that is, as the right–hand member 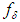 of equation (3) approaches (in the metric of the F) the exact value
of equation (3) approaches (in the metric of the F) the exact value 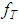 , the approximate solution
, the approximate solution 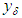 must approach (in the metric of the space) the exact solution
must approach (in the metric of the space) the exact solution 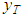 that we are seeking for in the equation
that we are seeking for in the equation 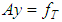 .Now, assuming that the elements
.Now, assuming that the elements 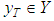 and
and 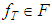 are connected by
are connected by 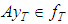 , we define the following concepts:Definition 2.1. An operator
, we define the following concepts:Definition 2.1. An operator 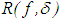 is said to be a regularizing operator for the equation
is said to be a regularizing operator for the equation 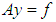 in a neighbourhood of
in a neighbourhood of 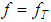 if:i) there exists a positive number
if:i) there exists a positive number 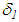 such that the operator
such that the operator 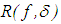 is defined for energy
is defined for energy 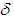 in
in 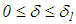 and every
and every 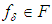 such that
such that 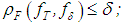 ii) for every
ii) for every 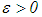 , there exists a
, there exists a 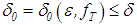 , such that the inequality
, such that the inequality 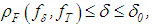 implies the inequality
implies the inequality 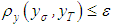 , where
, where 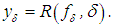 Definition 2.2. An operator
Definition 2.2. An operator 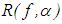 depending on a parameter α is called a regularizing operator for the equation Ay = f in a neighbourhood of
depending on a parameter α is called a regularizing operator for the equation Ay = f in a neighbourhood of 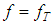 if:i) there exists a positive number
if:i) there exists a positive number 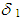 such that the operator
such that the operator 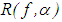 is defined for every
is defined for every 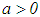 and every
and every 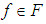 for which
for which 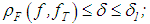 ii) there exists a function
ii) there exists a function 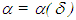 of
of 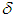 such that, for every
such that, for every 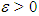 , there exists a number
, there exists a number 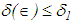 such that the inclusion
such that the inclusion 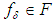 and the inequality
and the inequality 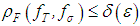 imply
imply 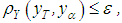 where
where 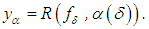 Again, there is no assumption of the uniqueness of the operator
Again, there is no assumption of the uniqueness of the operator 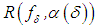 . It is easy to point out here that the function
. It is easy to point out here that the function 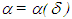 also depends on
also depends on 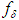 .If
.If 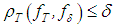 , we know from studies by Tikhonov [4] that we can take for an approximate solution of equation (3) with approximately known right–hand member
, we know from studies by Tikhonov [4] that we can take for an approximate solution of equation (3) with approximately known right–hand member 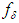 the element
the element 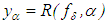 obtained with the aid of the regularizing operator
obtained with the aid of the regularizing operator 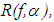 where
where 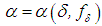 in accordance with the error in the initial data
in accordance with the error in the initial data 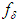 . This solution is called a regularized solution of equation (3). The numerical parameter α is called the regularization parameter. Obviously, every regularizing operator defines a stable method of approximate construction of the solution of equations (3) provided the choice of α is consistent with the accuracy
. This solution is called a regularized solution of equation (3). The numerical parameter α is called the regularization parameter. Obviously, every regularizing operator defines a stable method of approximate construction of the solution of equations (3) provided the choice of α is consistent with the accuracy 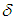 of the initial data
of the initial data 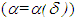 . If we know that
. If we know that 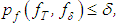 we can, by definition of a regularizing operator, choose the value of the regularization parameter
we can, by definition of a regularizing operator, choose the value of the regularization parameter 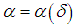 in such a way that, as
in such a way that, as 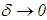 , the regularized solution
, the regularized solution 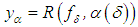 approaches (in the metric of Y) the desired exact solution
approaches (in the metric of Y) the desired exact solution 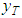 , that is,
, that is, 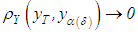 . This justifies taking as an approximate solution of equation (1) the regularized solution. Thus, the problem of finding an approximate solution of equation (1) that is stable under small changes in the right–hand member reduces to:i) finding regularizing operators;ii) determining the regularization parameter α from the supplementary information pertaining to the problem, for example, the size of the error in the right–hand member
. This justifies taking as an approximate solution of equation (1) the regularized solution. Thus, the problem of finding an approximate solution of equation (1) that is stable under small changes in the right–hand member reduces to:i) finding regularizing operators;ii) determining the regularization parameter α from the supplementary information pertaining to the problem, for example, the size of the error in the right–hand member 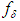 .This method of constructing approximate solutions is called the regularization method.Out of all the operators
.This method of constructing approximate solutions is called the regularization method.Out of all the operators 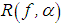 from F and Y that depend on the parameter α and which are defined for every f∈F and every positive α, we need to single out the operators that are continuous with respect to f. In doing this, we can give sufficient conditions for belonging to the set of regularizing operators of equation (3). This is an immediate consequence of the following theorem.Theorem 2.1. Let A denote an operator from Y into F and let
from F and Y that depend on the parameter α and which are defined for every f∈F and every positive α, we need to single out the operators that are continuous with respect to f. In doing this, we can give sufficient conditions for belonging to the set of regularizing operators of equation (3). This is an immediate consequence of the following theorem.Theorem 2.1. Let A denote an operator from Y into F and let 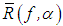 denote an operator from F into Y that is defined for every element f∈F and every positive α that is continuous with respect to f. If
denote an operator from F into Y that is defined for every element f∈F and every positive α that is continuous with respect to f. If 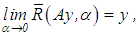 for every element y∈Y, then the operator
for every element y∈Y, then the operator 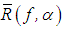 is a regularizing operator for the equation
is a regularizing operator for the equation 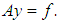 Proof. It will be sufficient to show that the operator
Proof. It will be sufficient to show that the operator 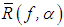 possesses property (ii) of Definition 2.2.Let
possesses property (ii) of Definition 2.2.Let 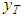 and
and 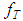 denote fixed elements of Y and F respectively such that
denote fixed elements of Y and F respectively such that 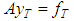 . Let
. Let 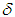 denote a fixed positive number. Then, for every element
denote a fixed positive number. Then, for every element 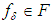 such that
such that 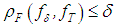 , we have
, we have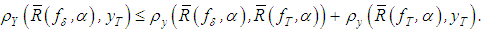 | (4) |
Since the operator 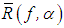 is continuous with respect to f at the “point”
is continuous with respect to f at the “point” 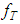 , it follows that, for sufficiently small positive
, it follows that, for sufficiently small positive 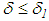 , the inequality
, the inequality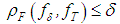 | (5) |
implies the inequality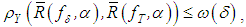 | (6) |
where 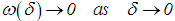 .Since
.Since 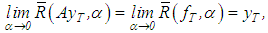 it holds that
it holds that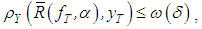 | (7) |
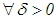 and
and 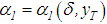 with
with 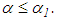 It follows from inequalities (4), (6), and (7) that, for every
It follows from inequalities (4), (6), and (7) that, for every 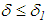 and
and 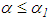 ,
,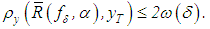 | (8) |
Since 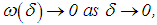 there exist for every
there exist for every 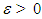 , a
, a 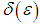 such that, for
such that, for 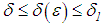 and
and 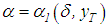 , inequalities (5) and (8) imply
, inequalities (5) and (8) imply 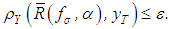 This completes the proof of Theorem 1.
This completes the proof of Theorem 1.
3. Regularization Methods
3.1. Tikhonov’s Regularization Method
Consider the Volterra integral equation of the first kind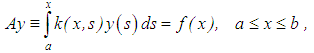 | (9) |
where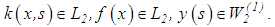 To ensure the stability of the solution of equation (9), we introduce the condition of minimum smoothing functional given as
To ensure the stability of the solution of equation (9), we introduce the condition of minimum smoothing functional given as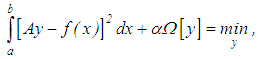 | (10) |
where, as it is so – called, the stabilizing functional, Ω[y], is usually written in the form [3]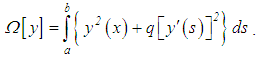 | (11) |
What is more, α > 0 is called the regularization parameter, 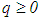 defines the order of the regularization (zero order if
defines the order of the regularization (zero order if 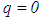 and first order if
and first order if 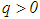 ). Expanding condition (10) using condition (11) and bearing in mind the Volterra structure of equation (9) yields the following equation of the second kind:
). Expanding condition (10) using condition (11) and bearing in mind the Volterra structure of equation (9) yields the following equation of the second kind: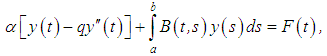 | (12) |
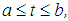 where
where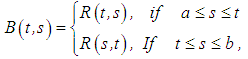 | (13) |
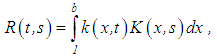 | (14) |
and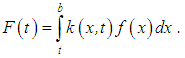 | (15) |
Expressions (13) and (14) may be written in another form as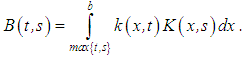 | (16) |
In place of equations (12) - (16), we may use the relation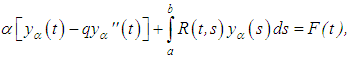 | (17) |
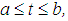 where
where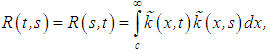 | (18) |
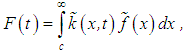 | (19) |
and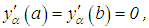 | (20) |
are valid for Fredholm first kind equation and setting in the later, 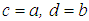 and
and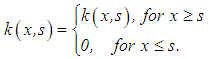 | (21) |
In all the cases considered above, the original Volterra integral equations of the first kind are replaced with equations of the second kind (precisely, integro-differential equation of the second kind) of Fredholm type. Consequently, the Tikhonov’s regularization method results in the loss of the Volterra structure but assists in the preliminary transformation of equation (10) (using, for example, the finite sum and the finite difference methods) into a system of linear algebraic equations with a full (positive definite) matrix (not triangular). This calls for a reasonable loss of time when solving it using any computational device. In spite of all these shortcomings, the use of Tikhonov’s regularization method in the solution of equation (9) still turns out to be one of the most effective of the regularization methods.
3.2. Tikhonov’s Regularization Method for Equation of Convolution type (Sequential Tikhonov Regularization Method)
We consider the convolution type Volterra integral equation of the first kind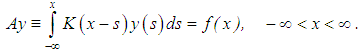 | (22) |
A complete discussion on this question has been provided by Savelova ([5], [6], [7], [8], [9], [10], [11]).For the convolution type Volterra integral equation of the first kind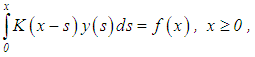 | (23) |
We first make use of the so-called techniques of extension [12]. We introduce the functions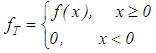 and
and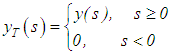 and hence obtain from equation (23), a new statement
and hence obtain from equation (23), a new statement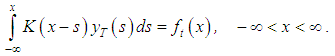 It is only from this moment that the Tikhonov’s regularization method may be applied.
It is only from this moment that the Tikhonov’s regularization method may be applied.
3.3. Denisov’s Regularization Method
Consider the equation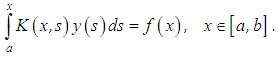 | (24) |
Let 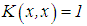 and the functions
and the functions 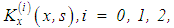 be continuous and the exact solution
be continuous and the exact solution 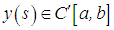 . What is more, let it be given that
. What is more, let it be given that 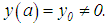 Suppose further, that in place of the right member
Suppose further, that in place of the right member 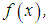 the approximate right member
the approximate right member 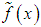 such that
such that 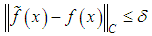 is known. Then, in place of equation (24), we propose the solution of the
is known. Then, in place of equation (24), we propose the solution of the 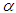 -regularizing equation
-regularizing equation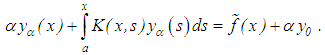 | (25) |
Such a procedure is close to the Lavrent-ev’s classical method. The asymptote of the solution of equation (25) is examined in the study by Blondel [13] when 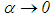 with the exact function
with the exact function 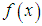 (but without the term
(but without the term 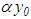 ).In the study by Denisov [14], it is proved that
).In the study by Denisov [14], it is proved that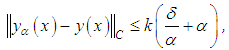 | (26) |
where k = constant. When 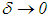 we select
we select 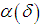 such that
such that 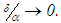 For instance, if
For instance, if 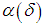 is chosen so that
is chosen so that 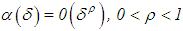 , we observe that
, we observe that 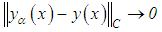 , which is the algorithm obtained from equation (24).We introduce yet another value of
, which is the algorithm obtained from equation (24).We introduce yet another value of 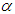 (call it the quasi-optimal regularizer and denote it by
(call it the quasi-optimal regularizer and denote it by 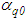 ), the minimizer of the right-hand side of equation (25). Hence, we obtain
), the minimizer of the right-hand side of equation (25). Hence, we obtain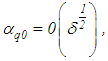 | (27) |
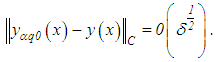 | (28) |
An important feature of the method under consideration is the simple nature of equation (24). Furthermore, the Volterra structure of the original equation (as seen) is maintained. However, the method insists on an initial knowledge of the value of 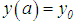 which, in a concrete situation, is not obtainable.
which, in a concrete situation, is not obtainable.
3.4. Apartsin’s 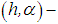 Regularization Method
Regularization Method
Further modification of Denisov’s 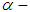 regularization method in conjunction with Apartsin–Bakushinskii’s
regularization method in conjunction with Apartsin–Bakushinskii’s 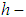 regularization method is called
regularization method is called 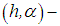 regularization method. In the said
regularization method. In the said 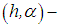 regularization method, it is clear from the onset that the procedure will involve the replacement of the integral of equation (24) with the corresponding approximate finite sum ( h-regularization) on the grid and instead of battling with the identification of the preconceived appropriate values of
regularization method, it is clear from the onset that the procedure will involve the replacement of the integral of equation (24) with the corresponding approximate finite sum ( h-regularization) on the grid and instead of battling with the identification of the preconceived appropriate values of 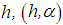 and
and 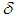 , a system of linear algebraic equations is put in place of equation (24) and is independent of
, a system of linear algebraic equations is put in place of equation (24) and is independent of 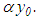 Now, we consider a system of linear algebraic equations with a triangular matrix of coefficients:
Now, we consider a system of linear algebraic equations with a triangular matrix of coefficients: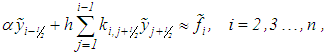 | (29) |
where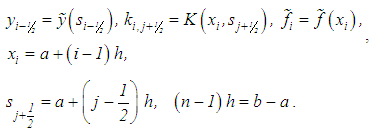 Notice that the system in equation (28) is obtained by replacing the integral in equation (24) with a finite sum defined by the mid-point rectangular formula having a step-size of h = constant.Let
Notice that the system in equation (28) is obtained by replacing the integral in equation (24) with a finite sum defined by the mid-point rectangular formula having a step-size of h = constant.Let 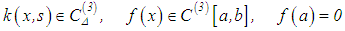 and
and 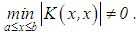 Then, for a regularized framework
Then, for a regularized framework 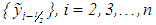 satisfying equation (29), the following estimate in respect of the error of the approximate solution is valid:
satisfying equation (29), the following estimate in respect of the error of the approximate solution is valid: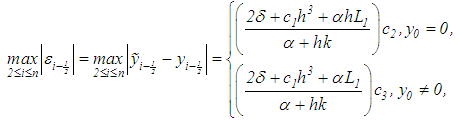 | (30) |
where 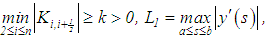
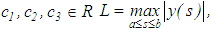
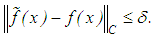 Let us analyze the estimate in equation (29). The first component on the right-hand side
Let us analyze the estimate in equation (29). The first component on the right-hand side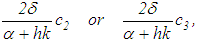 | (31) |
characterizes the influence on the exact regularized framework by the right-hand side error. The second component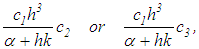 is connected with the approximation of the quadrature integral, while the third component
is connected with the approximation of the quadrature integral, while the third component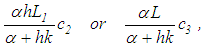 reflects the contribution of the total error of distortion of the desired equation (28) due to the additional
reflects the contribution of the total error of distortion of the desired equation (28) due to the additional  -component.It is seen that the error estimate in equation (29) unites the h–regularization estimate. This can be observed in equation (23) with the Denisov’s
-component.It is seen that the error estimate in equation (29) unites the h–regularization estimate. This can be observed in equation (23) with the Denisov’s 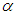 -regularization estimate in equation (25).We call the quasi-optimal regularizer (QOR) of the parameters
-regularization estimate in equation (25).We call the quasi-optimal regularizer (QOR) of the parameters 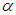 and h, the minimizer of the right-hand side of equation (29). This implies
and h, the minimizer of the right-hand side of equation (29). This implies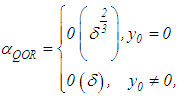 | (32) |
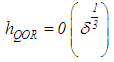 | (33) |
and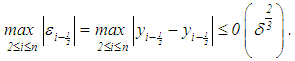 | (34) |
Since, in practice, it is not clear which of the cases results in 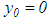 or
or 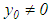 , it is, therefore, good to select one of the relationships in the equation (32) for the asymptote
, it is, therefore, good to select one of the relationships in the equation (32) for the asymptote 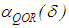 but maintaining the condition in equation (32). Indeed, if we set
but maintaining the condition in equation (32). Indeed, if we set 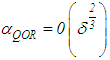 , then
, then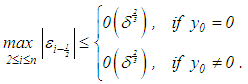 | (35) |
If we set 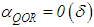 , then
, then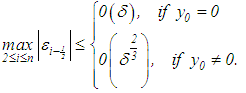 | (36) |
In all cases, however, 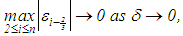 irrespective of whether
irrespective of whether 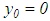 or
or 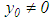 , that is, the algorithm obtained from solving the system of linear algebraic equation (28) and also equation (22) taking advantage of asymptotes (32) and (33) are regularized. Besides, unlike Denisov’s, the method does not use the
, that is, the algorithm obtained from solving the system of linear algebraic equation (28) and also equation (22) taking advantage of asymptotes (32) and (33) are regularized. Besides, unlike Denisov’s, the method does not use the 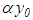 component, and the requirement of
component, and the requirement of 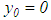 or
or 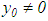 is compensated by changing the dependence of the quasi-optimal asymptote
is compensated by changing the dependence of the quasi-optimal asymptote 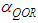 and
and 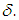 Finally, we note that as long as
Finally, we note that as long as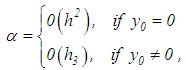 then as
then as 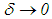 ,
, 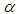 decreases faster than h (the carrier of the basic stability load) and so, parameters h and
decreases faster than h (the carrier of the basic stability load) and so, parameters h and 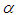 share homogeneous characterizations. As it now stands, the step size h should be regarded as the basic parameter while
share homogeneous characterizations. As it now stands, the step size h should be regarded as the basic parameter while 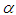 plays the role of the auxiliary. This is reflected by the fact that the presence or absence of
plays the role of the auxiliary. This is reflected by the fact that the presence or absence of 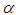 does not influence the state of the asymptote
does not influence the state of the asymptote 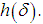 This being so, as soon as
This being so, as soon as 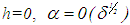 , the
, the 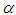 -smoothing equation quickly requires the presence of the component
-smoothing equation quickly requires the presence of the component 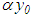 ; whereas, when h ≠ 0,
; whereas, when h ≠ 0, 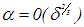 or
or 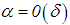 , the asymptote
, the asymptote 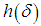 is such that it replaces the function of
is such that it replaces the function of 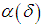 and continues to support the method of regularization without the introduction of the component
and continues to support the method of regularization without the introduction of the component 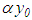 in the desired equation. However, the use of the parameter
in the desired equation. However, the use of the parameter 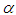 in place of h increases the effectiveness of the method since, for a small h (not to mention when h→0), the error of the solution is notably compressed.
in place of h increases the effectiveness of the method since, for a small h (not to mention when h→0), the error of the solution is notably compressed.
3.5. Sergeev’s Regularization Method
Consider Volterra integral equation of the first kind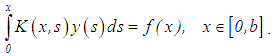 | (37) |
Let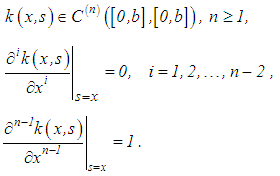 | (38) |
If 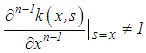 and
and 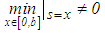 , we can divide both sides of equation (37) by
, we can divide both sides of equation (37) by 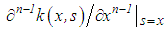 to obtain an equation with property (38).Now, let the function
to obtain an equation with property (38).Now, let the function 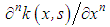 be continuous with respect to x and s. Let
be continuous with respect to x and s. Let 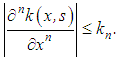 Then after the nth differentiation of equation (37), we obtain a second kind equation
Then after the nth differentiation of equation (37), we obtain a second kind equation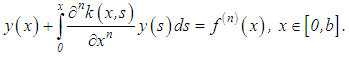 | (39) |
If 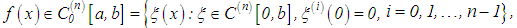 Then equation (39) has a unique solution
Then equation (39) has a unique solution 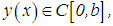 (by virtue of the given exact data). But, previously, it was assumed that
(by virtue of the given exact data). But, previously, it was assumed that 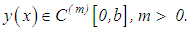 However, if f(x) together with the error is known, then the determination of the derivative f(n)(x) becomes an ill-posed problem and, hence, requires the use of any of the regularization methods. In the studies by Lavrent’ev et al and Sergeev ([15], [16]), a regularization method which also transforms the equation into a second kind equation but does not require the calculation of the said derivative of f(x) without losing the Volterra structure is proposed.Suppose the values
However, if f(x) together with the error is known, then the determination of the derivative f(n)(x) becomes an ill-posed problem and, hence, requires the use of any of the regularization methods. In the studies by Lavrent’ev et al and Sergeev ([15], [16]), a regularization method which also transforms the equation into a second kind equation but does not require the calculation of the said derivative of f(x) without losing the Volterra structure is proposed.Suppose the values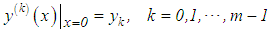 , are known. We introduce the function
, are known. We introduce the function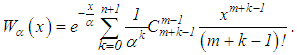 | (40) |
For this equation, let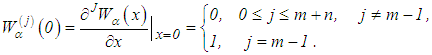 Let it be assumed that in place of the exact right – hand member f(x), the approximate right – hand member
Let it be assumed that in place of the exact right – hand member f(x), the approximate right – hand member 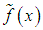 is known such that
is known such that 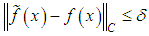 .Therefore, in place of the exact equation (37) or formally, its equivalent equation (39), we propose the solution of the following approximate Volterra equation of the second kind:
.Therefore, in place of the exact equation (37) or formally, its equivalent equation (39), we propose the solution of the following approximate Volterra equation of the second kind: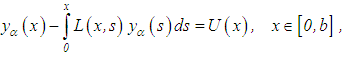 | (41) |
where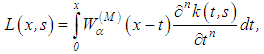
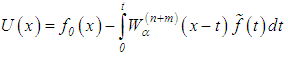 and
and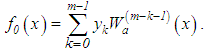 The estimate
The estimate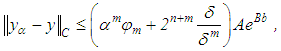 | (42) |
where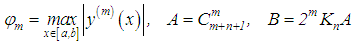 ,is valid. The minimum value of the right-hand side of equation (42) is obtained if
,is valid. The minimum value of the right-hand side of equation (42) is obtained if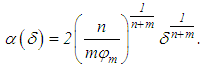 | (43) |
For such value of  ,
,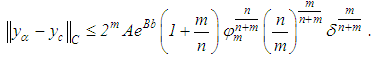 | (44) |
It is clear that 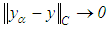 as
as 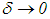 , and what is more,
, and what is more,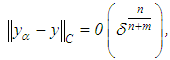 | (45) |
that is, the algorithm obtained from equation (41) is regularizing.In what appears to be the simplest case, where n = m = 1, it is expected to solve the equation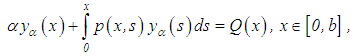 | (46) |
where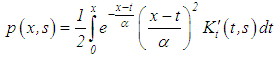 and
and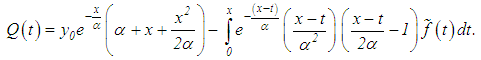 Consequently, we have that
Consequently, we have that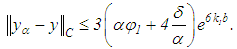 | (47) |
The minimum value of the right-hand side of equation (47) is attained when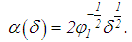 | (48) |
For such 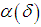 ,
,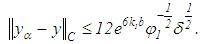 | (49) |
Here,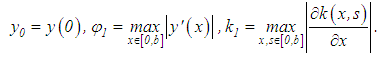
3.6. Magnicki’s Regularization Method
This is closely related to Sergeev’s method but has a wider range of applications. We consider the equation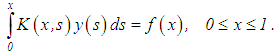 | (50) |
Let | (51) |
Furthermore, let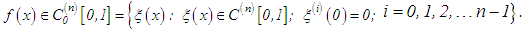 Then, differentiating equation (50) n times, we obtain the equation
Then, differentiating equation (50) n times, we obtain the equation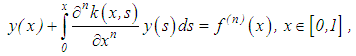 | (52) |
which has a unique solution 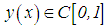 . Again, similar to Sergeev’s method, we assume that
. Again, similar to Sergeev’s method, we assume that 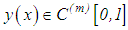 and that
and that 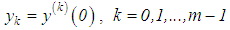 are known.Therefore, in place of equation (50) or (52), we propose the solution of a Volterra integral equation of the second kind
are known.Therefore, in place of equation (50) or (52), we propose the solution of a Volterra integral equation of the second kind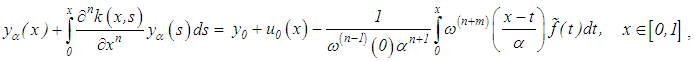 | (53) |
Subject to the conditions: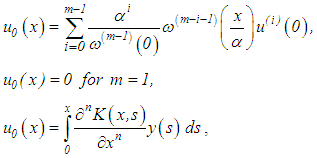
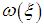 a class of functions defined by the following conditions:
a class of functions defined by the following conditions: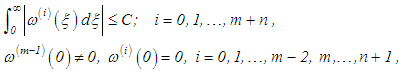 and there exist
and there exist 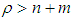 such that
such that 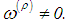 The following estimate is valid
The following estimate is valid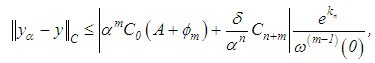 | (54) |
where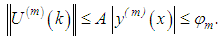 The minimum value of the right-hand side is attained when
The minimum value of the right-hand side is attained when 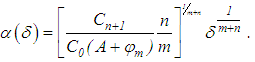 For such values of
For such values of 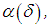
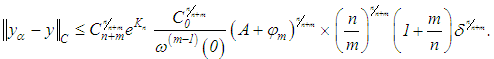 As
As 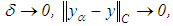 that is, the algorithm obtained from equation (53) is regularizing.For
that is, the algorithm obtained from equation (53) is regularizing.For 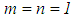 ,
, are continuous in x and s,
are continuous in x and s,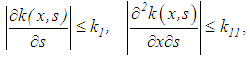 ,we propose a special equation (which is not necessarily a consequence of equation (53)):
,we propose a special equation (which is not necessarily a consequence of equation (53)):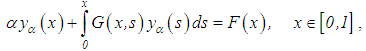 where
where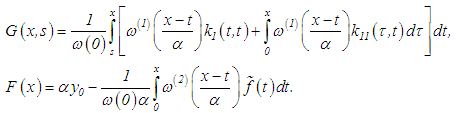 The following estimate (for an optimal value of
The following estimate (for an optimal value of 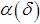 ) is valid:
) is valid: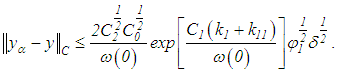 Now, with
Now, with 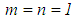 conditions similar to those of equation (51), it becomes necessary to solve the following consequence of equation (51):
conditions similar to those of equation (51), it becomes necessary to solve the following consequence of equation (51):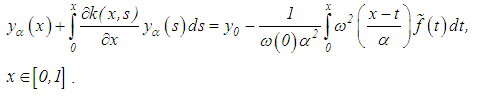 We obtain the following estimates
We obtain the following estimates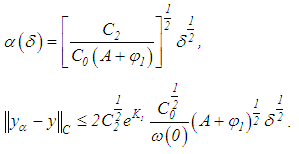
4. Conclusions
Although this study primarily examined regularization methods for first kind Volterra integral equations that maintain the Volterra structure, we never lost sight of the distinguishing features associated with this class of equations, which reflect in the uncertainty and difficulties surrounding their nature when attempting to find their solutions using one or other existing numerical methods. On the other hand, an attempt to solve Volterra integral equations of the first kind using analytic techniques may not be fruitful after all. This is so, because Volterra integral equations of the first kind, in a sense appears to be situated mid-way between Volterra integral equations of the second kind and Fredholm integral equation of the first kind. Precisely, if a Volterra integral equation of the second kind is well-posed and can be effectively solved by any classical means, then a Fredholm integral equation of the first kind is ill-posed, given any preconceived functional space and solvable by special approximating methods. Again, Volterra integral equation of the first kind may be well- posed or ill-posed depending on the choice of the solution space and can only be solved effectively by regularization methods.
References
| [1] | Tikhonov, A. N. and Arsenin, V. Y. (1977). Solutions of ill-posed Problems. Washington; Winston and Sons. |
| [2] | Apartsin, A. C. (1979). On numerical solution to integral equation of the first kind by regularization of quadrature method. Methods of optimization and its application 9; pp. 99-107. |
| [3] | Tikhonov, A. N. & Arsenin, A. A. (1979). Methods of solving ill-posed problems 2nd ed. Mir Publishes. Nauka: p. 288. |
| [4] | Tikhonov, A. N. (1963a). The solution of ill-posed problems, Doklady, Akad. Nauk SSSR, 151, 3. |
| [5] | Savelova, T. I. (1972). On a solution to convolution type equations with non- exact value of the kernel by regularization method. Journal of Applied Mathematics and mathematical Physics, 12, No. 1: pp. 212 – 218. |
| [6] | Savelova, T. I. (1974a). On the application of one clan of regularization algorithms for solving convolution type integral equations of the first kind in Banach Space. Journal of Applied Mathematics and Mathematical Physics, 14, No.2: pp. 479 – 483. |
| [7] | Savelova, T. I. (1974b). Projectional method of solving linear ill- posed problems. Journal of Applied Mathematics and Mathematical Physics 14, No. 4: pp. 1027 – 1031. |
| [8] | Savelova, T. I. (1975a). On regularization of convolution type integral equations of the first kind, Journal of Applied Mathematics and Mathematical Physics, 15, No. 2: pp, 298 – 304. |
| [9] | Savelova, T. I. (1975b). On regularization of system of linear convolution type integral equations of the first kind. Journal of Applied Mathematics and Mathematical Physics, 15, No. 6: pp. 1381 – 1388. |
| [10] | Savelova, T. I. (1978a). About optimal regularization of convolution type equations with Approximate Right-hand Member and Kernel. Journal of Applied Mathematics and Mathematical Physics, 18, No. 1: pp. 218 – 222. |
| [11] | Savelova, T. I. (1978b). About optimal regularization of convolution type equations with sudden charges in the values of the right-hand number and the Kernel. Journal of Applied Mathematics and Mathematical Physics, 18, No. 2: pp. 275 – 283. |
| [12] | Gakhov, F. D. & Cherskii, Ya. I. (1978). Convolution type equations. Mir. Publishes, Nauka: p. 296. |
| [13] | Blondel, J. M. (1971). Phenomene de pertubation singuliere pour une equation integrale lineaire de Volterra. Ibid., 5, No 3: pp. 67 – 72. |
| [14] | Denisov, A. M. (1975). The approximate solution of a volterra equation of the first kind, Journal of Computation Mathematics and Mathematical Phyiscs, 15, No 4: pp. 237 – 239. |
| [15] | Lavrent ev’, M. M., Romanov, V. G. & Shishatskii, S. P. (1980). Ill-posed problems of mathematical physics and analysis. Mir Publishes, Nauka: p. 288. |
| [16] | Sergeev, V. O. (1971). Regularization of Volterra’s Equations of the First Kind. DAN SSSR, 197, No. 3: pp. 531 – 534. |


 and the right-hand side
and the right-hand side 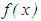 are known without error and that the approximating equation can be exact, whereas, as is often the case, these may not be true. Consequently, the effect can be observed in the study of regularization methods for solving Volterra type integral equations of the first kind. Classical regularization methods tend to destroy the non-anticipatory (or causal) nature of the original Volterra problem because such methods typically rely on the computation of the Volterra adjoint operator. In this paper, we highlight the general concept of the regularization method of solution for Volterra integral equation of the first kind without destroying the Volterra structure.
are known without error and that the approximating equation can be exact, whereas, as is often the case, these may not be true. Consequently, the effect can be observed in the study of regularization methods for solving Volterra type integral equations of the first kind. Classical regularization methods tend to destroy the non-anticipatory (or causal) nature of the original Volterra problem because such methods typically rely on the computation of the Volterra adjoint operator. In this paper, we highlight the general concept of the regularization method of solution for Volterra integral equation of the first kind without destroying the Volterra structure.
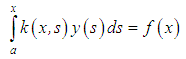
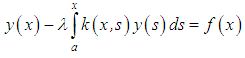
 are real numbers,
are real numbers, 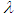 is a parameter,
is a parameter, 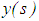 is an unknown function, while
is an unknown function, while 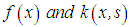 are given functions which are square integrable on
are given functions which are square integrable on 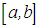 and in the domain
and in the domain 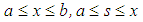 respectively. The function
respectively. The function 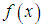 is called the free term, while the function
is called the free term, while the function 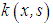 is called the kernel.One distinguishing feature associated with this class of equations is the uncertainty surrounding their nature and this is reflected in the difficulties encountered when attempting to find their solutions using one or the other of the existing numerical methods [2]. On one hand, Volterra integral equations of the first kind appear to be special cases of Fredholm integral equations of the first kind and are consequently classified among the lists of ill-conditioned problems solvable by the classical regularization means. On the other hand, given a set of limitations (for example, given that their kernels and right-hand sides are “good” and “smooth”) Volterra integral equations of the first kind belong to the class of well-posed problems and hence can be solved through any direct method based on the discretization of the unknown solutions. Both approaches seem to be a little on the extreme. The use of discretization process transforms Volterra integral equations of the first kind into another problem (often systems of linear equations and may be solved by the well-known singular value decomposition) that can lead to solutions which may or may not deviate strongly from the (minimum norm) solution of the original equation [3]. A complete regularization (with its accompanying difficulties and unresolved questions) turns out to be a too complicated approach as it is observed that the methods for Volterra equations of the first kind are not nearly as ill-posed as methods for Fredholm integral equations of the first kind.In this study, we investigate the regularization methods with a view to identifying the properties and types that can be used in solving Volterra type equations of the first kind, but without destroying the Volterra structure. The methods in view are perhaps the discrete regularization methods. The discrete approximation methods provide another approach to regularize the original problem. In this case, the regularization parameter is the discretization parameter (or step size) and coordination between this parameter and the amount of noise
is called the kernel.One distinguishing feature associated with this class of equations is the uncertainty surrounding their nature and this is reflected in the difficulties encountered when attempting to find their solutions using one or the other of the existing numerical methods [2]. On one hand, Volterra integral equations of the first kind appear to be special cases of Fredholm integral equations of the first kind and are consequently classified among the lists of ill-conditioned problems solvable by the classical regularization means. On the other hand, given a set of limitations (for example, given that their kernels and right-hand sides are “good” and “smooth”) Volterra integral equations of the first kind belong to the class of well-posed problems and hence can be solved through any direct method based on the discretization of the unknown solutions. Both approaches seem to be a little on the extreme. The use of discretization process transforms Volterra integral equations of the first kind into another problem (often systems of linear equations and may be solved by the well-known singular value decomposition) that can lead to solutions which may or may not deviate strongly from the (minimum norm) solution of the original equation [3]. A complete regularization (with its accompanying difficulties and unresolved questions) turns out to be a too complicated approach as it is observed that the methods for Volterra equations of the first kind are not nearly as ill-posed as methods for Fredholm integral equations of the first kind.In this study, we investigate the regularization methods with a view to identifying the properties and types that can be used in solving Volterra type equations of the first kind, but without destroying the Volterra structure. The methods in view are perhaps the discrete regularization methods. The discrete approximation methods provide another approach to regularize the original problem. In this case, the regularization parameter is the discretization parameter (or step size) and coordination between this parameter and the amount of noise 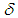 in the problem is required to obtain good approximations in the presence of noise.
in the problem is required to obtain good approximations in the presence of noise.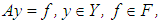
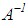 is also continuous in the set
is also continuous in the set 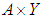 and the set Y of possible solutions, is not compact.If the right–hand member of the equation is an element
and the set Y of possible solutions, is not compact.If the right–hand member of the equation is an element 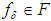 that differs from the exact right–hand member
that differs from the exact right–hand member 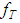 by no more than
by no more than 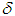 , that is, if
, that is, if 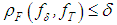 , it is obvious that the approximate solutions
, it is obvious that the approximate solutions 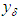 of equation (3) cannot be defined as the exact solution of this equation with approximate right–hand member
of equation (3) cannot be defined as the exact solution of this equation with approximate right–hand member 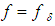 , that is, according to the formula
, that is, according to the formula 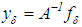 .The numerical parameter
.The numerical parameter 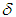 characterizes the error in the right–hand member of equation (3). Therefore, it is natural to define
characterizes the error in the right–hand member of equation (3). Therefore, it is natural to define 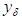 with the aid of an operator depending on a parameter having a value chosen in accordance with the error
with the aid of an operator depending on a parameter having a value chosen in accordance with the error 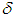 in the initial data
in the initial data 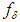 . Specifically, as
. Specifically, as 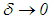 , that is, as the right–hand member
, that is, as the right–hand member 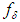 of equation (3) approaches (in the metric of the F) the exact value
of equation (3) approaches (in the metric of the F) the exact value 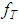 , the approximate solution
, the approximate solution 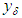 must approach (in the metric of the space) the exact solution
must approach (in the metric of the space) the exact solution 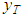 that we are seeking for in the equation
that we are seeking for in the equation 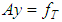 .Now, assuming that the elements
.Now, assuming that the elements 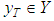 and
and 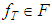 are connected by
are connected by 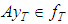 , we define the following concepts:Definition 2.1. An operator
, we define the following concepts:Definition 2.1. An operator 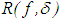 is said to be a regularizing operator for the equation
is said to be a regularizing operator for the equation 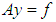 in a neighbourhood of
in a neighbourhood of 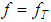 if:i) there exists a positive number
if:i) there exists a positive number 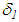 such that the operator
such that the operator 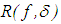 is defined for energy
is defined for energy 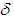 in
in 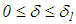 and every
and every 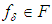 such that
such that 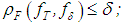 ii) for every
ii) for every 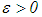 , there exists a
, there exists a 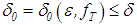 , such that the inequality
, such that the inequality 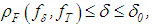 implies the inequality
implies the inequality 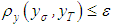 , where
, where 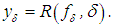 Definition 2.2. An operator
Definition 2.2. An operator 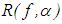 depending on a parameter α is called a regularizing operator for the equation Ay = f in a neighbourhood of
depending on a parameter α is called a regularizing operator for the equation Ay = f in a neighbourhood of 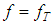 if:i) there exists a positive number
if:i) there exists a positive number 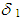 such that the operator
such that the operator 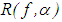 is defined for every
is defined for every 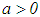 and every
and every 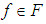 for which
for which 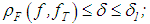 ii) there exists a function
ii) there exists a function 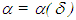 of
of 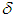 such that, for every
such that, for every 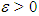 , there exists a number
, there exists a number 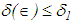 such that the inclusion
such that the inclusion 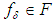 and the inequality
and the inequality 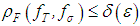 imply
imply 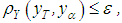 where
where 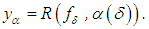 Again, there is no assumption of the uniqueness of the operator
Again, there is no assumption of the uniqueness of the operator 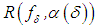 . It is easy to point out here that the function
. It is easy to point out here that the function 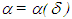 also depends on
also depends on 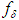 .If
.If 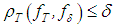 , we know from studies by Tikhonov [4] that we can take for an approximate solution of equation (3) with approximately known right–hand member
, we know from studies by Tikhonov [4] that we can take for an approximate solution of equation (3) with approximately known right–hand member 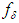 the element
the element 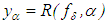 obtained with the aid of the regularizing operator
obtained with the aid of the regularizing operator 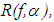 where
where 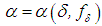 in accordance with the error in the initial data
in accordance with the error in the initial data 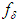 . This solution is called a regularized solution of equation (3). The numerical parameter α is called the regularization parameter. Obviously, every regularizing operator defines a stable method of approximate construction of the solution of equations (3) provided the choice of α is consistent with the accuracy
. This solution is called a regularized solution of equation (3). The numerical parameter α is called the regularization parameter. Obviously, every regularizing operator defines a stable method of approximate construction of the solution of equations (3) provided the choice of α is consistent with the accuracy 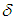 of the initial data
of the initial data 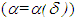 . If we know that
. If we know that 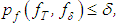 we can, by definition of a regularizing operator, choose the value of the regularization parameter
we can, by definition of a regularizing operator, choose the value of the regularization parameter 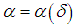 in such a way that, as
in such a way that, as 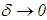 , the regularized solution
, the regularized solution 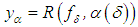 approaches (in the metric of Y) the desired exact solution
approaches (in the metric of Y) the desired exact solution 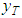 , that is,
, that is, 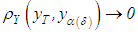 . This justifies taking as an approximate solution of equation (1) the regularized solution. Thus, the problem of finding an approximate solution of equation (1) that is stable under small changes in the right–hand member reduces to:i) finding regularizing operators;ii) determining the regularization parameter α from the supplementary information pertaining to the problem, for example, the size of the error in the right–hand member
. This justifies taking as an approximate solution of equation (1) the regularized solution. Thus, the problem of finding an approximate solution of equation (1) that is stable under small changes in the right–hand member reduces to:i) finding regularizing operators;ii) determining the regularization parameter α from the supplementary information pertaining to the problem, for example, the size of the error in the right–hand member 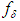 .This method of constructing approximate solutions is called the regularization method.Out of all the operators
.This method of constructing approximate solutions is called the regularization method.Out of all the operators 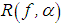 from F and Y that depend on the parameter α and which are defined for every f∈F and every positive α, we need to single out the operators that are continuous with respect to f. In doing this, we can give sufficient conditions for belonging to the set of regularizing operators of equation (3). This is an immediate consequence of the following theorem.Theorem 2.1. Let A denote an operator from Y into F and let
from F and Y that depend on the parameter α and which are defined for every f∈F and every positive α, we need to single out the operators that are continuous with respect to f. In doing this, we can give sufficient conditions for belonging to the set of regularizing operators of equation (3). This is an immediate consequence of the following theorem.Theorem 2.1. Let A denote an operator from Y into F and let 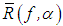 denote an operator from F into Y that is defined for every element f∈F and every positive α that is continuous with respect to f. If
denote an operator from F into Y that is defined for every element f∈F and every positive α that is continuous with respect to f. If 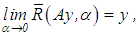 for every element y∈Y, then the operator
for every element y∈Y, then the operator 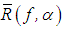 is a regularizing operator for the equation
is a regularizing operator for the equation 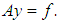 Proof. It will be sufficient to show that the operator
Proof. It will be sufficient to show that the operator 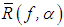 possesses property (ii) of Definition 2.2.Let
possesses property (ii) of Definition 2.2.Let 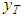 and
and 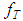 denote fixed elements of Y and F respectively such that
denote fixed elements of Y and F respectively such that 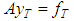 . Let
. Let 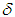 denote a fixed positive number. Then, for every element
denote a fixed positive number. Then, for every element 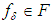 such that
such that 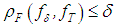 , we have
, we have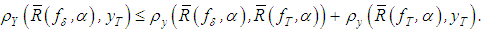
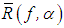 is continuous with respect to f at the “point”
is continuous with respect to f at the “point” 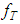 , it follows that, for sufficiently small positive
, it follows that, for sufficiently small positive 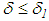 , the inequality
, the inequality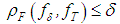
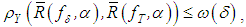
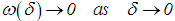 .Since
.Since 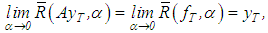 it holds that
it holds that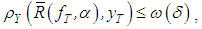
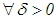 and
and 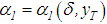 with
with 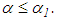 It follows from inequalities (4), (6), and (7) that, for every
It follows from inequalities (4), (6), and (7) that, for every 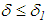 and
and 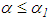 ,
,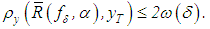
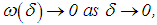 there exist for every
there exist for every 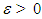 , a
, a 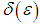 such that, for
such that, for 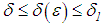 and
and 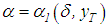 , inequalities (5) and (8) imply
, inequalities (5) and (8) imply 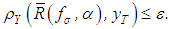 This completes the proof of Theorem 1.
This completes the proof of Theorem 1.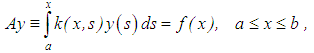
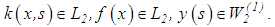 To ensure the stability of the solution of equation (9), we introduce the condition of minimum smoothing functional given as
To ensure the stability of the solution of equation (9), we introduce the condition of minimum smoothing functional given as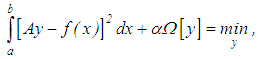
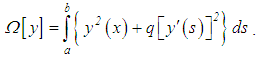
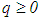 defines the order of the regularization (zero order if
defines the order of the regularization (zero order if 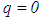 and first order if
and first order if 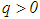 ). Expanding condition (10) using condition (11) and bearing in mind the Volterra structure of equation (9) yields the following equation of the second kind:
). Expanding condition (10) using condition (11) and bearing in mind the Volterra structure of equation (9) yields the following equation of the second kind: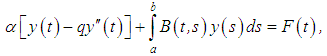
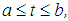 where
where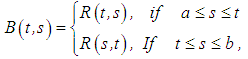
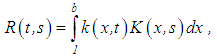
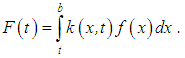
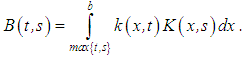
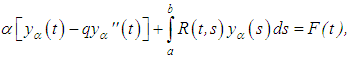
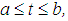 where
where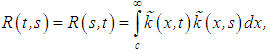
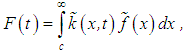
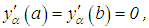
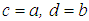 and
and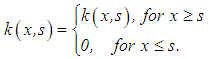
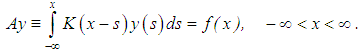
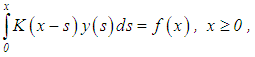
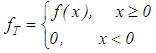 and
and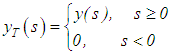 and hence obtain from equation (23), a new statement
and hence obtain from equation (23), a new statement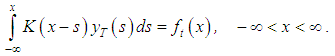 It is only from this moment that the Tikhonov’s regularization method may be applied.
It is only from this moment that the Tikhonov’s regularization method may be applied.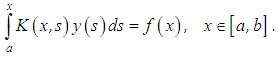
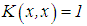 and the functions
and the functions 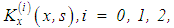 be continuous and the exact solution
be continuous and the exact solution 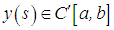 . What is more, let it be given that
. What is more, let it be given that 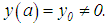 Suppose further, that in place of the right member
Suppose further, that in place of the right member 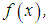 the approximate right member
the approximate right member 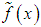 such that
such that 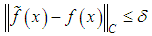 is known. Then, in place of equation (24), we propose the solution of the
is known. Then, in place of equation (24), we propose the solution of the 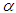 -regularizing equation
-regularizing equation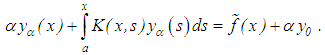
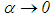 with the exact function
with the exact function 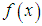 (but without the term
(but without the term 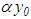 ).In the study by Denisov [14], it is proved that
).In the study by Denisov [14], it is proved that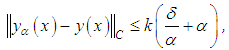
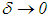 we select
we select 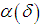 such that
such that 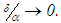 For instance, if
For instance, if 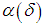 is chosen so that
is chosen so that 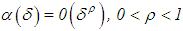 , we observe that
, we observe that 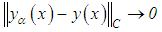 , which is the algorithm obtained from equation (24).We introduce yet another value of
, which is the algorithm obtained from equation (24).We introduce yet another value of 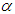 (call it the quasi-optimal regularizer and denote it by
(call it the quasi-optimal regularizer and denote it by 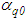 ), the minimizer of the right-hand side of equation (25). Hence, we obtain
), the minimizer of the right-hand side of equation (25). Hence, we obtain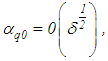
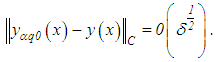
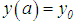 which, in a concrete situation, is not obtainable.
which, in a concrete situation, is not obtainable.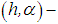 Regularization Method
Regularization Method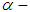 regularization method in conjunction with Apartsin–Bakushinskii’s
regularization method in conjunction with Apartsin–Bakushinskii’s 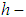 regularization method is called
regularization method is called 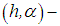 regularization method. In the said
regularization method. In the said 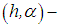 regularization method, it is clear from the onset that the procedure will involve the replacement of the integral of equation (24) with the corresponding approximate finite sum ( h-regularization) on the grid and instead of battling with the identification of the preconceived appropriate values of
regularization method, it is clear from the onset that the procedure will involve the replacement of the integral of equation (24) with the corresponding approximate finite sum ( h-regularization) on the grid and instead of battling with the identification of the preconceived appropriate values of 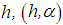 and
and 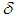 , a system of linear algebraic equations is put in place of equation (24) and is independent of
, a system of linear algebraic equations is put in place of equation (24) and is independent of 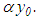 Now, we consider a system of linear algebraic equations with a triangular matrix of coefficients:
Now, we consider a system of linear algebraic equations with a triangular matrix of coefficients: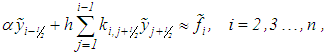
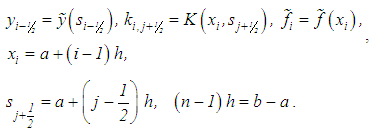 Notice that the system in equation (28) is obtained by replacing the integral in equation (24) with a finite sum defined by the mid-point rectangular formula having a step-size of h = constant.Let
Notice that the system in equation (28) is obtained by replacing the integral in equation (24) with a finite sum defined by the mid-point rectangular formula having a step-size of h = constant.Let 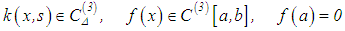 and
and 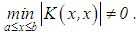 Then, for a regularized framework
Then, for a regularized framework 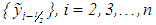 satisfying equation (29), the following estimate in respect of the error of the approximate solution is valid:
satisfying equation (29), the following estimate in respect of the error of the approximate solution is valid: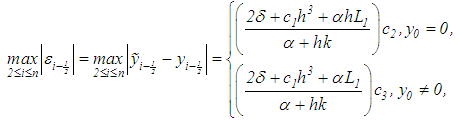
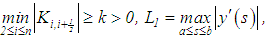
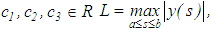
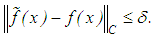 Let us analyze the estimate in equation (29). The first component on the right-hand side
Let us analyze the estimate in equation (29). The first component on the right-hand side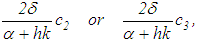
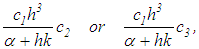 is connected with the approximation of the quadrature integral, while the third component
is connected with the approximation of the quadrature integral, while the third component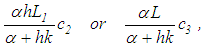 reflects the contribution of the total error of distortion of the desired equation (28) due to the additional
reflects the contribution of the total error of distortion of the desired equation (28) due to the additional 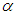 -component.It is seen that the error estimate in equation (29) unites the h–regularization estimate. This can be observed in equation (23) with the Denisov’s
-component.It is seen that the error estimate in equation (29) unites the h–regularization estimate. This can be observed in equation (23) with the Denisov’s 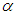 -regularization estimate in equation (25).We call the quasi-optimal regularizer (QOR) of the parameters
-regularization estimate in equation (25).We call the quasi-optimal regularizer (QOR) of the parameters 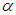 and h, the minimizer of the right-hand side of equation (29). This implies
and h, the minimizer of the right-hand side of equation (29). This implies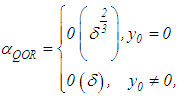
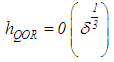
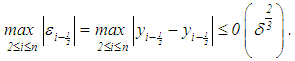
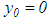 or
or 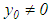 , it is, therefore, good to select one of the relationships in the equation (32) for the asymptote
, it is, therefore, good to select one of the relationships in the equation (32) for the asymptote 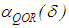 but maintaining the condition in equation (32). Indeed, if we set
but maintaining the condition in equation (32). Indeed, if we set 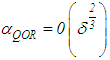 , then
, then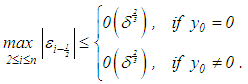
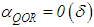 , then
, then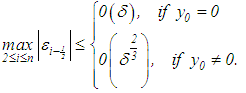
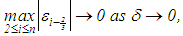 irrespective of whether
irrespective of whether 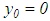 or
or 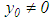 , that is, the algorithm obtained from solving the system of linear algebraic equation (28) and also equation (22) taking advantage of asymptotes (32) and (33) are regularized. Besides, unlike Denisov’s, the method does not use the
, that is, the algorithm obtained from solving the system of linear algebraic equation (28) and also equation (22) taking advantage of asymptotes (32) and (33) are regularized. Besides, unlike Denisov’s, the method does not use the 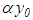 component, and the requirement of
component, and the requirement of 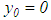 or
or 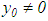 is compensated by changing the dependence of the quasi-optimal asymptote
is compensated by changing the dependence of the quasi-optimal asymptote 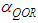 and
and 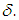 Finally, we note that as long as
Finally, we note that as long as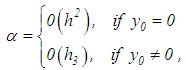 then as
then as 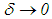 ,
, 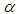 decreases faster than h (the carrier of the basic stability load) and so, parameters h and
decreases faster than h (the carrier of the basic stability load) and so, parameters h and 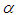 share homogeneous characterizations. As it now stands, the step size h should be regarded as the basic parameter while
share homogeneous characterizations. As it now stands, the step size h should be regarded as the basic parameter while 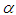 plays the role of the auxiliary. This is reflected by the fact that the presence or absence of
plays the role of the auxiliary. This is reflected by the fact that the presence or absence of 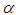 does not influence the state of the asymptote
does not influence the state of the asymptote 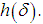 This being so, as soon as
This being so, as soon as 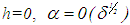 , the
, the 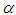 -smoothing equation quickly requires the presence of the component
-smoothing equation quickly requires the presence of the component 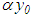 ; whereas, when h ≠ 0,
; whereas, when h ≠ 0, 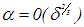 or
or 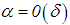 , the asymptote
, the asymptote 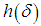 is such that it replaces the function of
is such that it replaces the function of 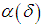 and continues to support the method of regularization without the introduction of the component
and continues to support the method of regularization without the introduction of the component 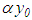 in the desired equation. However, the use of the parameter
in the desired equation. However, the use of the parameter 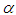 in place of h increases the effectiveness of the method since, for a small h (not to mention when h→0), the error of the solution is notably compressed.
in place of h increases the effectiveness of the method since, for a small h (not to mention when h→0), the error of the solution is notably compressed.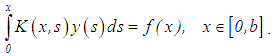
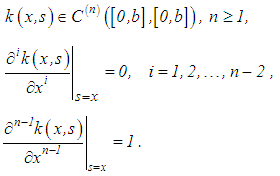
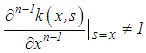 and
and 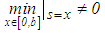 , we can divide both sides of equation (37) by
, we can divide both sides of equation (37) by 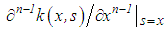 to obtain an equation with property (38).Now, let the function
to obtain an equation with property (38).Now, let the function 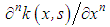 be continuous with respect to x and s. Let
be continuous with respect to x and s. Let 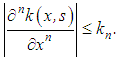 Then after the nth differentiation of equation (37), we obtain a second kind equation
Then after the nth differentiation of equation (37), we obtain a second kind equation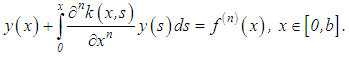
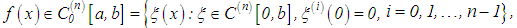 Then equation (39) has a unique solution
Then equation (39) has a unique solution 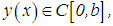 (by virtue of the given exact data). But, previously, it was assumed that
(by virtue of the given exact data). But, previously, it was assumed that 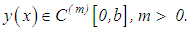 However, if f(x) together with the error is known, then the determination of the derivative f(n)(x) becomes an ill-posed problem and, hence, requires the use of any of the regularization methods. In the studies by Lavrent’ev et al and Sergeev ([15], [16]), a regularization method which also transforms the equation into a second kind equation but does not require the calculation of the said derivative of f(x) without losing the Volterra structure is proposed.Suppose the values
However, if f(x) together with the error is known, then the determination of the derivative f(n)(x) becomes an ill-posed problem and, hence, requires the use of any of the regularization methods. In the studies by Lavrent’ev et al and Sergeev ([15], [16]), a regularization method which also transforms the equation into a second kind equation but does not require the calculation of the said derivative of f(x) without losing the Volterra structure is proposed.Suppose the values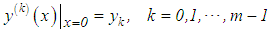 , are known. We introduce the function
, are known. We introduce the function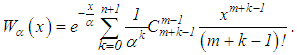
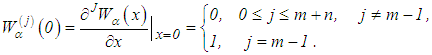 Let it be assumed that in place of the exact right – hand member f(x), the approximate right – hand member
Let it be assumed that in place of the exact right – hand member f(x), the approximate right – hand member 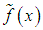 is known such that
is known such that 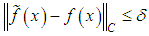 .Therefore, in place of the exact equation (37) or formally, its equivalent equation (39), we propose the solution of the following approximate Volterra equation of the second kind:
.Therefore, in place of the exact equation (37) or formally, its equivalent equation (39), we propose the solution of the following approximate Volterra equation of the second kind: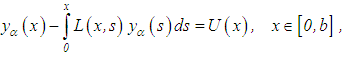
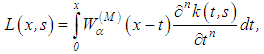
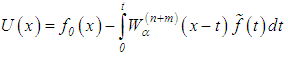 and
and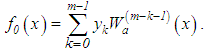 The estimate
The estimate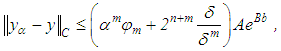
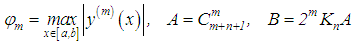 ,is valid. The minimum value of the right-hand side of equation (42) is obtained if
,is valid. The minimum value of the right-hand side of equation (42) is obtained if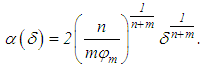
 ,
,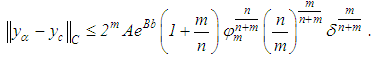
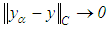 as
as 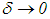 , and what is more,
, and what is more,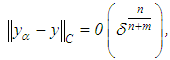
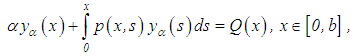
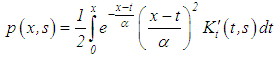 and
and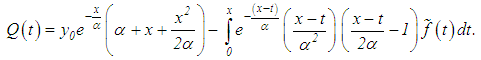 Consequently, we have that
Consequently, we have that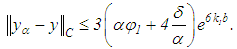
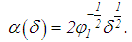
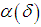 ,
,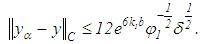
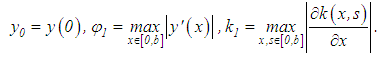
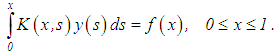

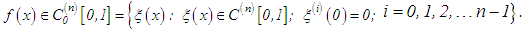 Then, differentiating equation (50) n times, we obtain the equation
Then, differentiating equation (50) n times, we obtain the equation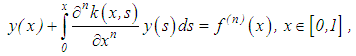
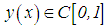 . Again, similar to Sergeev’s method, we assume that
. Again, similar to Sergeev’s method, we assume that 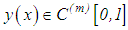 and that
and that 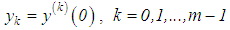 are known.Therefore, in place of equation (50) or (52), we propose the solution of a Volterra integral equation of the second kind
are known.Therefore, in place of equation (50) or (52), we propose the solution of a Volterra integral equation of the second kind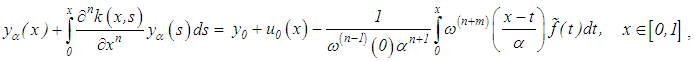
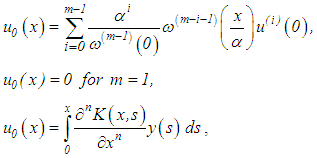
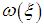 a class of functions defined by the following conditions:
a class of functions defined by the following conditions: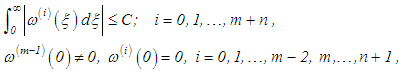 and there exist
and there exist 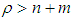 such that
such that 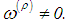 The following estimate is valid
The following estimate is valid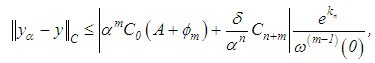
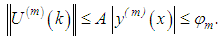 The minimum value of the right-hand side is attained when
The minimum value of the right-hand side is attained when 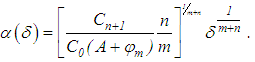 For such values of
For such values of 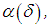
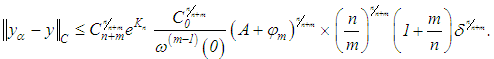 As
As 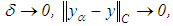 that is, the algorithm obtained from equation (53) is regularizing.For
that is, the algorithm obtained from equation (53) is regularizing.For  ,
, are continuous in x and s,
are continuous in x and s,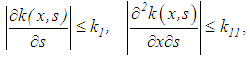 ,we propose a special equation (which is not necessarily a consequence of equation (53)):
,we propose a special equation (which is not necessarily a consequence of equation (53)):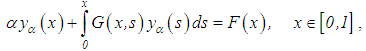 where
where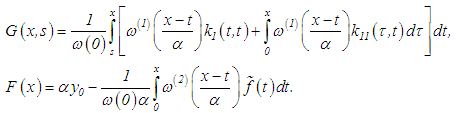 The following estimate (for an optimal value of
The following estimate (for an optimal value of 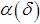 ) is valid:
) is valid: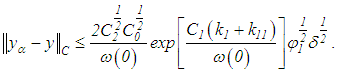 Now, with
Now, with 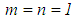 conditions similar to those of equation (51), it becomes necessary to solve the following consequence of equation (51):
conditions similar to those of equation (51), it becomes necessary to solve the following consequence of equation (51):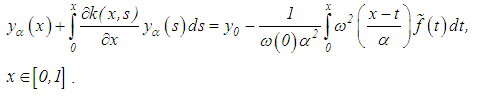 We obtain the following estimates
We obtain the following estimates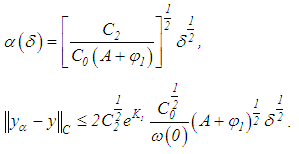
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML