1. Introduction

An investigation was made concerning the average waiting time for the purchase of food items in the students’ cafeteria of one of the universities in the sub-Sahara region. The purpose is to give a relevant recommendation concerning food services. This in its effect would certainly extend to the recreational services, works and maintenance department educational services such as the library, bookshop and a host of others. This work critically examines the queue system as it applies to the cafeteria section/department of the sampled (selected) university, and it is thus tailored towards giving necessary recommendations in general.

2. Definitions

A queue is an array of items which are expecting services [3] [10]. The services may either be direct or indirect. Several types of queues-services relationship exist of which each of them serves different purposes. For the purpose of this finding, we shall adopt the single queue to single service point. This is also referred to as simple queue [10]. The method of simple queue is characterized with the following features; it is available to customers on first come, first served basis, there is no limit placed on the queue length, the items are discrete in value, and the probability distribution of arrival pattern assumes Poisson approximately. (A special case of the binomial distribution is called the Poisson distribution. Its representation assumes discrete probability distribution. For instance, 0 , 1 , 2 , … , may be the number of arrivals within a stipulated or specified period. The time interval assume any positive value, thus it is a continuous probability distribution.) [3], and it is called first in first out. The principle here states that customers are served one at a time and that the customer that has been waiting the longest is served first [6]. Queue, in general, may be formed at any place, when customers (human beings or physical entities) that require service are gathered. Crises occur due to the fact that the number of customers exceeds the number of service facilities. It can also occur when service facilities do not work efficiently or whenever it takes more than what is required to serve a customer.

3. History of the Concept in Brief

The waiting line theory was formally known as the queuing theory This development was owed to A.K Erlang who in 1903 took up the problem on congestion of telephone traffic. [9] The difficulty was that during busy periods, telephone operators were unable to handle the calls the moment they were made, giving rise to delayed calls. A.k Erlang directed his first efforts at finding the delay for one operator and later on the results were extended to finding the delay for several operators. The field of telephone traffic was further developed by Molins (1927) and Thornton D-fry (1928). [3] [6] [8] However, it was only after World War II that this early work was extended to other general problems involving queues or waiting lines. The ideas have since seen applications including telecommunication, traffic engineering, computing [2] and, particularly in industrial engineering, in the design of factories, shops, offices and hospitals, as well as in project management. [7] [4].

4. Justification of the Theory and Its Application

We can find waiting lines or queues almost everywhere. Business of all types, industries, schools, hospitals, cafeterias, book stores or shops, libraries, banks, post offices, petrol stations, theatres – all have queuing problems. Queues (waiting lines) can also be found in workshops where the machines wait to be repaired; at a tool crib where the mechanics wait to receive tools; in a warehouse where items wait to be used; incoming calls wait to mature in the telephone exchange; trucks wait to be unloaded; airplanes wait either to take-off or land and so on. For the purpose of this research activity, a case study of a university cafeteria is vividly considered.

5. Investigation at the Cafeteria

The following data was collected from the eatery section of the university. This was done in order to ascertain the condition of services rendered as concerned with daily meals purchased most especially by the students of the institution, so that by observations, necessary and relevant recommendations could be offered for further development and improvements.

Table 1

Average waiting time for the purchase of food item between 7.38 AM and 8.30 AM (52minutes)

From the table, total time on operation = 52min.

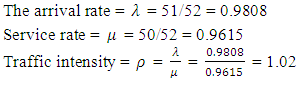
6. Interpretation

This system does not fully agree with a simple queue characteristics. This is simply due to the fact that the traffic intensity 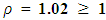. If an approximation is made, in which, 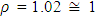, then this might be interpreted to mean that we have an average of a customer on queue at any given point in time. The queue system observed here is undoubtedly not perfect enough even though it is still manageable considering the fact that adjustment can still be made and necessary modality put in place in order to have better improvements.

7. Implications and Consequences

Case of this nature needs some orientations. One of such is to acquaint the constituted authority of some of the characteristics of customers otherwise referred to as the customer’s behavior of waiting, such as (i) Balking in which customers deciding not to join the queue if it is too long (ii) Jockeying where customers switch between queues if they think they will get served faster by doing so and (iii) Reneging, a situation where customers leave the queue if they have waited too long for service. This means that all hands must be on deck by the constituted authority in making sure that all necessary arrangements and adjustments are put in place for sanitization so as to improve the sales and services by the cafeteria. This will enable an impressive turn out of customers in patronizing the venture which will eventually enhance continuity of the business. Similar recommendation is also suggested for other sections such as the supermarkets, recreation center, health center (very important- since they are dealing with lives which is very precious). Another consequence is the fact that if there is no improvement in the quality of service delivery, it may result to what is known as the negative exponential probability in which the probability of a short service time may be highest with reducing probability of longer services time. Thus the assumption of a more appropriate distribution such as the symmetrical normal distribution [1] makes the analysis exceedingly complex and renders simulation necessary [3]. Also, the cost consideration has to be determined. The study of Queuing theory helps to determine the balance between two conflicting costs which are (i) the cost of offering the service and (ii) the cost incurred due to delay in offering service. The first cost may associate with the service facilities and their operation, and the second can represent the cost of customers waiting to be served. Furthermore waiting line problems arise either because there happens to be too much demand on the facilities so that we say that there is excess of waiting time or inadequacy in the number of service facilities or when there is too less demand, in which case there is too much idle facility time or too many facilities. In either case, the problem is to either schedule arrivals or provides proper number of facilities or both so as to obtain an optimum balance between the cost associated with waiting time and idle time. It is obvious that an increase in the existing service facilities would reduce the customer’s waiting time. On the contrary, decreasing the level of service may result in long queue. This means an increase in the level of service increases the cost of operating the service facilities but on the other hand, decreases the cost of customers waiting for the service.

8. Conclusions

It is worth nothing that payments are given to the staff who render services to customers in queue system, for this singular reason, our interest is also extended to the total cost of the services, ways and means of stepping down such cost without necessarily lowering the standard of service; this would in a way accrue profits to the university venture.