Min-Hai Huang
College of Mathematics and Statistics, Zhaoqing University, Zhaoqing, Guang Dong, China
Correspondence to: Min-Hai Huang, College of Mathematics and Statistics, Zhaoqing University, Zhaoqing, Guang Dong, China.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A Dirichlet boundary-value problem for the modified Helmholtz equation in the quarter-plane was discussed. By using the Fokas transform method, the solution in the form of integral representation was given.
Keywords:
Modified Helmholtz equation, Boundary-value problem, Fokas transform method
Cite this paper: Min-Hai Huang, A Dirichlet Boundary-Value Problem in the Quarter-Plane for the Modified Helmholtz Equation, Applied Mathematics, Vol. 8 No. 2, 2018, pp. 26-29. doi: 10.5923/j.am.20180802.02.
1. Introduction
The aim of this paper is to solve a Dirichlet boundary-value problem of the modified Helmholtz equation in a quarter-plane. The modified Helmholtz equation arises naturally in many physical applications [1], for example, in implicit marching schemes for the heat equation, in Debye-Huckel theory, in the linearization of the Poisson-Boltzmann equation, in diffusion of waves [2, 3, 4] and so on.The mathematical formulation of our problem is as follow. Find a function 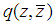 in the first quadrant
in the first quadrant 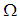 satisfying
satisfying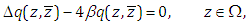 | (1.1) |
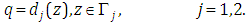 | (1.2) |
where 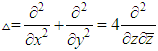 is the usual Laplace operator,
is the usual Laplace operator, 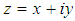 and
and 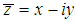 ,
, 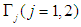 is the borderline of the wedge domain
is the borderline of the wedge domain 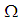 ,
, 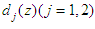 is known function and
is known function and 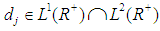 , the
, the 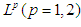 spaces are function spaces defined on
spaces are function spaces defined on 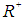 using a natural generalization of the p-norm for finite-dimensional vector spaces.Classical integral transform methods such as Fourier transform, Laplace and Mellin transform are important mathematical tools in investigating boundary-value problems of partial differential equations (see [5, 6]). For one concrete boundary value problem, appropriate integral transformation should be applied. Here, we shall use the Fokas transform method [7].In the late 1990s Fokas introduced a novel flexible approach to solve the initial/boundary value problem for various two dimensional linear and integrable nonlinear PDE's [8]. In general, Fokas transform method involves three steps, namely:(i) given a PDE, construct a closed differential form (this is related to the existence of a Lax pair);(ii) given a domain, perform the spectral analysis associated with this differential form, yields an integral representation of the solution in terms of boundary value of the domain;(iii) given appropriate boundary conditions, by analyzing the global relation, the unknown boundary values can be determined.The main achievement of this method is that it yields explicit integral (as oppose to series) representations for a variety of boundary value problems. For some specific problems, the integral representation of the solutions have analytical and numerical advantage, and also facilitate to analysis the asymptotic behavior of the solution. Use of Fokas transform to construct the integral expression of solutions is valid for convex polygons, but fail for non-convex polygon. The readers are also referred to [7] for a systematic exposition of the method, its various applications and more references therein.
using a natural generalization of the p-norm for finite-dimensional vector spaces.Classical integral transform methods such as Fourier transform, Laplace and Mellin transform are important mathematical tools in investigating boundary-value problems of partial differential equations (see [5, 6]). For one concrete boundary value problem, appropriate integral transformation should be applied. Here, we shall use the Fokas transform method [7].In the late 1990s Fokas introduced a novel flexible approach to solve the initial/boundary value problem for various two dimensional linear and integrable nonlinear PDE's [8]. In general, Fokas transform method involves three steps, namely:(i) given a PDE, construct a closed differential form (this is related to the existence of a Lax pair);(ii) given a domain, perform the spectral analysis associated with this differential form, yields an integral representation of the solution in terms of boundary value of the domain;(iii) given appropriate boundary conditions, by analyzing the global relation, the unknown boundary values can be determined.The main achievement of this method is that it yields explicit integral (as oppose to series) representations for a variety of boundary value problems. For some specific problems, the integral representation of the solutions have analytical and numerical advantage, and also facilitate to analysis the asymptotic behavior of the solution. Use of Fokas transform to construct the integral expression of solutions is valid for convex polygons, but fail for non-convex polygon. The readers are also referred to [7] for a systematic exposition of the method, its various applications and more references therein.
2. The Integral Representation of the Solution
LEMMA 1. ([7]) Let 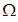 be the interior of the first quadrant of the complex z-plane. Assume that there exists a solution
be the interior of the first quadrant of the complex z-plane. Assume that there exists a solution 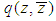 of the modified Helmholtz equation (1.1) in
of the modified Helmholtz equation (1.1) in 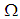 , and assume that this solution is sufficiently smooth on the boundary of
, and assume that this solution is sufficiently smooth on the boundary of 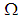 . Then
. Then 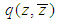 can be expressed as
can be expressed as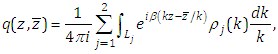 | (2.1) |
where the spectral functions 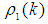 and
and 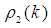 are defined as
are defined as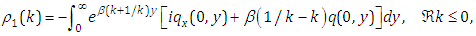 | (2.2) |
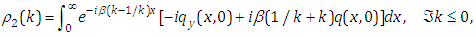 | (2.3) |
and the rays 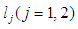 are respectively the positive imaginary axis and the positive real axis in the complex
are respectively the positive imaginary axis and the positive real axis in the complex 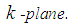 Furthermore, the following global relation is valid:
Furthermore, the following global relation is valid: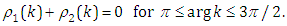 | (2.4) |
3. Determination of the Spectral Functions
In the section 2, the solutions of (1.1) has been given in Lemma 1 in the form of integral representation (2.1) with spectral functions 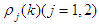 , which involve both the Dirichlet and Neumann boundary-values. For the concrete problem, some boundary-values are unknown. But, this can be achieved by help of the global relations and certain symmetrical properties. In this section, we'll give an derivation of the procedure.Theorem 1. Assume that
, which involve both the Dirichlet and Neumann boundary-values. For the concrete problem, some boundary-values are unknown. But, this can be achieved by help of the global relations and certain symmetrical properties. In this section, we'll give an derivation of the procedure.Theorem 1. Assume that 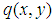 is a solution of the modified Helmholtz equation (1.1) in the first quadrant
is a solution of the modified Helmholtz equation (1.1) in the first quadrant 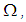 and satisfies the Dirichlet boundary condition (1.2), then it possesses the integral representation
and satisfies the Dirichlet boundary condition (1.2), then it possesses the integral representation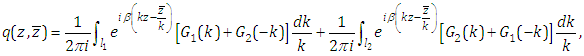 | (3.1) |
where, the rays 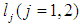 are respectively the positive imaginary axis and the positive real axis in the complex
are respectively the positive imaginary axis and the positive real axis in the complex 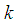 -plane, and
-plane, and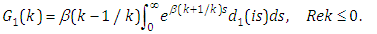 | (3.2) |
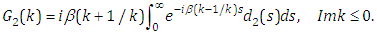 | (3.3) |
Proof: First of all, we introduce two auxiliary functions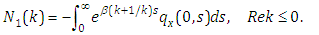 | (3.4) |
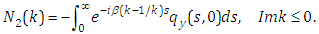 | (3.5) |
Now, we have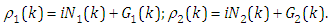 | (3.6) |
Then, it's easy to see, 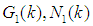 and
and 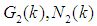 are analytic functions in the left and lower half
are analytic functions in the left and lower half 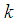 -planes, respectively, and fulfill the readily verified symmetrical relations
-planes, respectively, and fulfill the readily verified symmetrical relations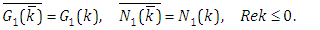 | (3.7) |
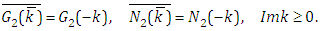 | (3.8) |
From the global relation (2.4), we have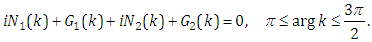 | (3.9) |
Taking complex conjugates for the formula (3.9), according to the symmetry relations (3.7)-(3.8), we obtain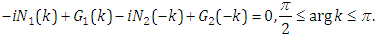 | (3.10) |
which is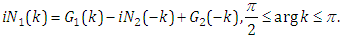 | (3.11) |
Formula (3.9) add (3.10) yields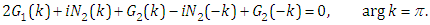 | (3.12) |
Making transform 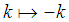 , we have
, we have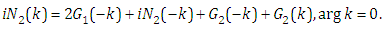 | (3.13) |
Combining the formulas (3.13), (3.11), (3.6) and (2.1), one obtains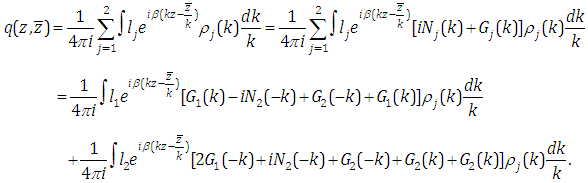 | (3.14) |
By using Cauchy's integral theorem, it's easy deduced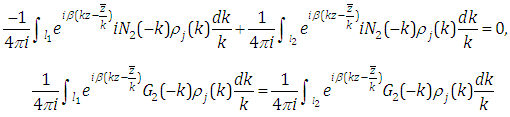 | (3.15) |
It is readily seen that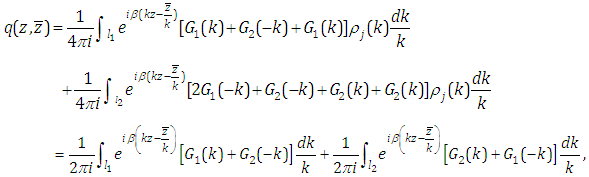 | (3.16) |
which justifies (3.1).
4. Conclusions
In this paper, we have used Fokas transform method to discuss a Dirichlet boundary-value problem for the modified Helmholtz equation in the quarter-plane. We deduced the formula of the spectral function in detail, and the solution in the form of integral representation was obtained. It was shown that the integral representations of the solution is closed, which is useful for further analysis of the solution (see [9]).The Fokas’ transform method is a powerful tool for solving problems of the initial/boundary value problem for various two dimensional linear and integrable nonlinear PDE's. This paper presents a simple application. To some extent, Fokas transform is an effective complement and promote of the Fourier transform and the inverse scattering transform.
ACKNOWLEDGEMENTS
This research was supported by the Provincial Key Platforms and Major Scientific Research Projects of Guangdong Universities (No: 504-20160146). The author is very grateful to the reviewers for their good comments and hard work.
References
| [1] | H. W. Cheng, J. F. Huang and T. J. Leiterman, An adaptive fast solver for the modified Helmholtz equation in two dimensions, J. Comput. Phys., 211(2006), 616-637. |
| [2] | A. E. H. Juffer, E. F. F. Botta, B. A. M. van Keulen, A. van der Ploeg, H. J. C. Berendsen, The electric potential of a macromolecule in a solvent: A fundamental approach, Journal of Computational Physics, 97(1) (1991), 144-171. |
| [3] | J. Liang, S. Subramaniam, Computation of molecular electrostatics with bound- ary ele- ment methods. Biophysical Journal, 73(4) (1997), 1830-1841. |
| [4] | D. ben-Avraham and A. S. Fokas, The solution of the modified Helmholtz equation in a wedge and an application to diffusion-limited coalescence, Phys. Lett. A, 263(1999), 355- 359. |
| [5] | R. N. Bracewell, The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw- Hill, I, 2000. |
| [6] | A. D. Polyanin and A. V. Manzhirov, Handbook of Integral Equations, Boca Raton: CRC Press, 1998. |
| [7] | A. S. Fokas, A unified approach to boundary value problems, SIAM, Philadelphia, 2008. |
| [8] | A. S. Fokas, A unified transform method for solving linear and certain nonlinear PDEs, Proc. Roy. Soc. London Ser. A, 453(1997), 1411-1443. |
| [9] | M.-H. Huang and Y.-Q. Zhao, High-frequency asymptotics for the modified Helmholtz equation in a quarter-plane, Appl. Anal., 90(2011), 1927-1938. |



 in the first quadrant
in the first quadrant 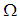 satisfying
satisfying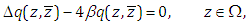
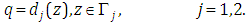
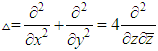 is the usual Laplace operator,
is the usual Laplace operator, 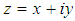 and
and 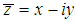 ,
, 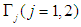 is the borderline of the wedge domain
is the borderline of the wedge domain 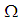 ,
, 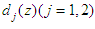 is known function and
is known function and 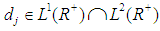 , the
, the 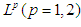 spaces are function spaces defined on
spaces are function spaces defined on 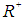 using a natural generalization of the p-norm for finite-dimensional vector spaces.Classical integral transform methods such as Fourier transform, Laplace and Mellin transform are important mathematical tools in investigating boundary-value problems of partial differential equations (see [5, 6]). For one concrete boundary value problem, appropriate integral transformation should be applied. Here, we shall use the Fokas transform method [7].In the late 1990s Fokas introduced a novel flexible approach to solve the initial/boundary value problem for various two dimensional linear and integrable nonlinear PDE's [8]. In general, Fokas transform method involves three steps, namely:(i) given a PDE, construct a closed differential form (this is related to the existence of a Lax pair);(ii) given a domain, perform the spectral analysis associated with this differential form, yields an integral representation of the solution in terms of boundary value of the domain;(iii) given appropriate boundary conditions, by analyzing the global relation, the unknown boundary values can be determined.The main achievement of this method is that it yields explicit integral (as oppose to series) representations for a variety of boundary value problems. For some specific problems, the integral representation of the solutions have analytical and numerical advantage, and also facilitate to analysis the asymptotic behavior of the solution. Use of Fokas transform to construct the integral expression of solutions is valid for convex polygons, but fail for non-convex polygon. The readers are also referred to [7] for a systematic exposition of the method, its various applications and more references therein.
using a natural generalization of the p-norm for finite-dimensional vector spaces.Classical integral transform methods such as Fourier transform, Laplace and Mellin transform are important mathematical tools in investigating boundary-value problems of partial differential equations (see [5, 6]). For one concrete boundary value problem, appropriate integral transformation should be applied. Here, we shall use the Fokas transform method [7].In the late 1990s Fokas introduced a novel flexible approach to solve the initial/boundary value problem for various two dimensional linear and integrable nonlinear PDE's [8]. In general, Fokas transform method involves three steps, namely:(i) given a PDE, construct a closed differential form (this is related to the existence of a Lax pair);(ii) given a domain, perform the spectral analysis associated with this differential form, yields an integral representation of the solution in terms of boundary value of the domain;(iii) given appropriate boundary conditions, by analyzing the global relation, the unknown boundary values can be determined.The main achievement of this method is that it yields explicit integral (as oppose to series) representations for a variety of boundary value problems. For some specific problems, the integral representation of the solutions have analytical and numerical advantage, and also facilitate to analysis the asymptotic behavior of the solution. Use of Fokas transform to construct the integral expression of solutions is valid for convex polygons, but fail for non-convex polygon. The readers are also referred to [7] for a systematic exposition of the method, its various applications and more references therein.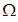 be the interior of the first quadrant of the complex z-plane. Assume that there exists a solution
be the interior of the first quadrant of the complex z-plane. Assume that there exists a solution 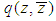 of the modified Helmholtz equation (1.1) in
of the modified Helmholtz equation (1.1) in 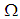 , and assume that this solution is sufficiently smooth on the boundary of
, and assume that this solution is sufficiently smooth on the boundary of 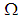 . Then
. Then 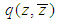 can be expressed as
can be expressed as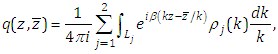
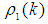 and
and 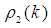 are defined as
are defined as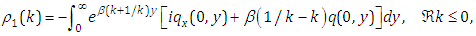
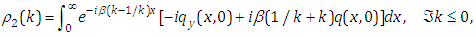
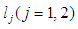 are respectively the positive imaginary axis and the positive real axis in the complex
are respectively the positive imaginary axis and the positive real axis in the complex 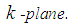 Furthermore, the following global relation is valid:
Furthermore, the following global relation is valid: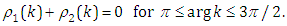
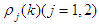 , which involve both the Dirichlet and Neumann boundary-values. For the concrete problem, some boundary-values are unknown. But, this can be achieved by help of the global relations and certain symmetrical properties. In this section, we'll give an derivation of the procedure.Theorem 1. Assume that
, which involve both the Dirichlet and Neumann boundary-values. For the concrete problem, some boundary-values are unknown. But, this can be achieved by help of the global relations and certain symmetrical properties. In this section, we'll give an derivation of the procedure.Theorem 1. Assume that 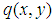 is a solution of the modified Helmholtz equation (1.1) in the first quadrant
is a solution of the modified Helmholtz equation (1.1) in the first quadrant 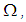 and satisfies the Dirichlet boundary condition (1.2), then it possesses the integral representation
and satisfies the Dirichlet boundary condition (1.2), then it possesses the integral representation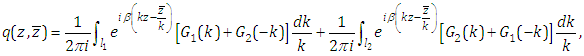
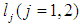 are respectively the positive imaginary axis and the positive real axis in the complex
are respectively the positive imaginary axis and the positive real axis in the complex  -plane, and
-plane, and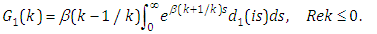
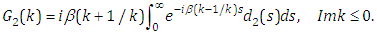
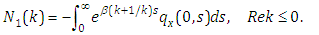
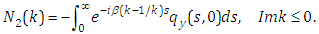
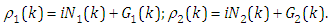
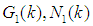 and
and 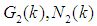 are analytic functions in the left and lower half
are analytic functions in the left and lower half 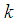 -planes, respectively, and fulfill the readily verified symmetrical relations
-planes, respectively, and fulfill the readily verified symmetrical relations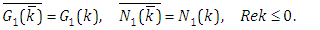
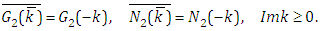
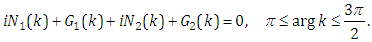
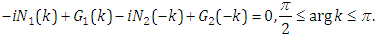
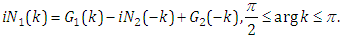
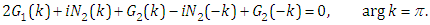
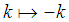 , we have
, we have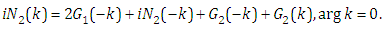
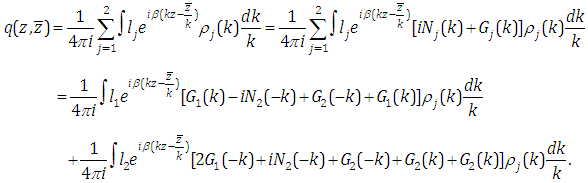
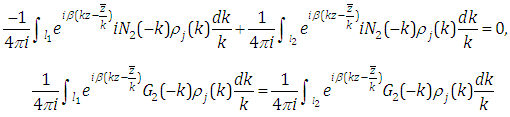
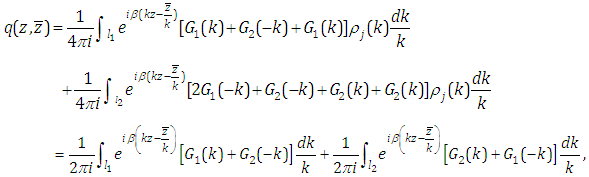
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML