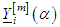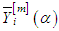-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2018; 8(2): 19-25
doi:10.5923/j.am.20180802.01

Numerical Solution of Nth-Order Fuzzy Differential Equations by Third Order Runge Kutta Method Based on Combination of Arithmatics, Harmonics and Geometrics Means
1Department of Informatics, STMIK Amik Riau, Pekanbaru, Indonesia
2Department of Informatics, STIKOM Pelita, Pekanbaru, Indonesia
Correspondence to: Yanti Rini, Department of Informatics, STMIK Amik Riau, Pekanbaru, Indonesia.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We discuss a numerical solution of Nth-order fuzzy differential equations with initial value by third order Runge Kutta method based on combination of arithmatics, harmonics and geometrics means. Moreover, the convergence, stability and error analysis also discussed. The algorithm is illustrated by solving the Nth-order of fuzzy initial value problem. The numerical simulation show that the new method worked and give an accurate solution.
Keywords: Fuzzy numbers, Nth-order fuzzy Initial value problem, Runge Kutta method, Lipschitz condition
Cite this paper: Yanti Rini, Hajjah Alyauma, Numerical Solution of Nth-Order Fuzzy Differential Equations by Third Order Runge Kutta Method Based on Combination of Arithmatics, Harmonics and Geometrics Means, Applied Mathematics, Vol. 8 No. 2, 2018, pp. 19-25. doi: 10.5923/j.am.20180802.01.
Article Outline
1. Introduction
- Every physical problem is inherently biased by uncertainty. There is often a need to model, solve, and interpret the problems one encounters in the world of uncertainty. To overcome this uncertainty and vague, we may use the interval and fuzzy set theory. The topic of fuzzy differential equations (FDEs) forms a suitable setting for mathematical modelling of this physical problems. The concept of fuzzy derivative was first introduced by Chang and Zadeh (1972). Numerical solution for linear fuzzy differential equation was studied by many researcher ([1], [2], [3], [4], [5], [6], [7], [8], [9]). The solution of n-th order of fuzzy differential equation also derive by [10], [11], [12], [13] and [14]. The most frequently method to get the numerical solution is Runge Kutta method.This paper studied a third order Runge Kutta method based on combination of arithmatics, harmonics and geometrics mean to solve n-th order of fuzzy initial value problem. In the Section 2, we begin with some preliminary results and concepts about fuzzy number and system of fuzzy initial value problem. In Section 3, we discuss the main idea to solve the problem. We also analyse the stability, convergence and the error, then we employ the method on test example. Finally, in Section 4 we give the conclusion of this study.
2. Preliminaries
2.1. A Fuzzy Number
- An interval
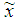 is denoted by
is denoted by 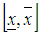 on the set of real numbers R given by
on the set of real numbers R given by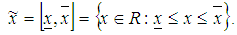 In this paper, we have only considered closed intervals, although there exist various types of intervals such as open and half-open intervals. A fuzzy number
In this paper, we have only considered closed intervals, although there exist various types of intervals such as open and half-open intervals. A fuzzy number 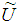 is convex, normalized fuzzy set
is convex, normalized fuzzy set 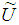 of the real line
of the real line 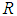 such that
such that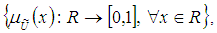 where,
where, 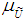 is called the membership function of the fuzzy set, and it is piecewise continuous. A triangular fuzzy number
is called the membership function of the fuzzy set, and it is piecewise continuous. A triangular fuzzy number 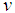 is defined by three numbers
is defined by three numbers 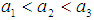 , where the graph of
, where the graph of 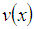 , the member of function of the fuzzy number
, the member of function of the fuzzy number 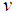 , is a triangle with the base on the interval
, is a triangle with the base on the interval 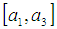 and the vertex at
and the vertex at 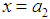 . We specify
. We specify 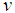 as
as 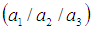 and
and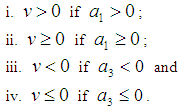 Let
Let 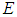 be a set of all the upper semicontinuous normal convex fuzzy numbers with bounded r-level sets. It means that if
be a set of all the upper semicontinuous normal convex fuzzy numbers with bounded r-level sets. It means that if 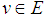 , then the
, then the 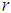 -level set
-level set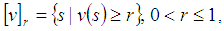 is a closed bounded interval which is denoted by
is a closed bounded interval which is denoted by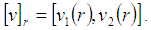 Let
Let 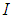 be a real interval. The mapping
be a real interval. The mapping 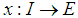 is called fuzzy process and its
is called fuzzy process and its 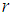 -level set is denoted by
-level set is denoted by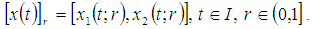 The derivative
The derivative 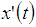 of the fuzzy process x is defined by
of the fuzzy process x is defined by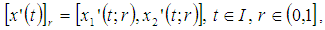 provided that this equation determines the fuzzy number.Let
provided that this equation determines the fuzzy number.Let 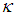 be the set of all nonempty compact subset of
be the set of all nonempty compact subset of 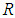 and
and 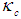 be the subset of
be the subset of 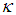 consisting of nonempty convex compact sets. Recall that
consisting of nonempty convex compact sets. Recall that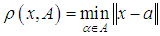 is a distance of the point
is a distance of the point 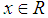 from
from 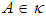 and that the Hausdorff separation
and that the Hausdorff separation 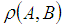 of
of 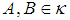 is defined as
is defined as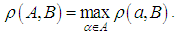
2.2. A nth Fuzzy Initial Value Problem
- Consider the fuzzy initial value problem
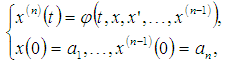 | (1) |
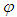 is continuous mapping from
is continuous mapping from 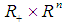 into
into 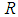 and
and 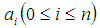 are fuzzy numbers in
are fuzzy numbers in 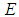 . The
. The 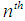 -order fuzzy differential equation by changing variables
-order fuzzy differential equation by changing variables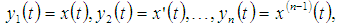 converts to the following fuzzy system
converts to the following fuzzy system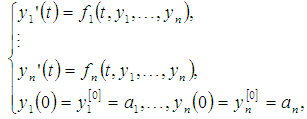 | (2) |
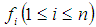 are continuous mapping from
are continuous mapping from 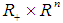 into
into 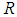 and
and 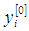 are fuzzy numbers in
are fuzzy numbers in 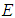 with
with 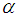 -level intervals
-level intervals 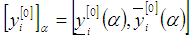 for
for 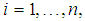 and
and 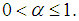 Now, we have to show that the solution of (2) is
Now, we have to show that the solution of (2) is 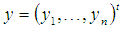 on a interval
on a interval 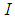 , if
, if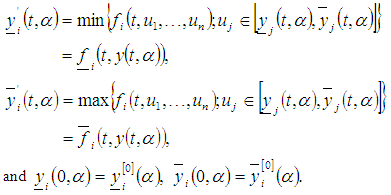 For fixed value
For fixed value 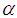 , we have a system of initial value problem in
, we have a system of initial value problem in 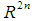 and we have intervals
and we have intervals 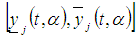 with a fuzzy number
with a fuzzy number 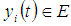 . Let
. Let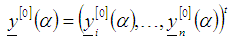 and
and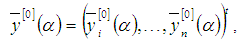 with respect to the indicators system (2) can be written as with assumption
with respect to the indicators system (2) can be written as with assumption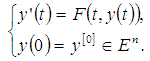 | (3) |
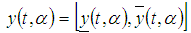 and
and 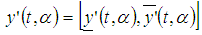 where
where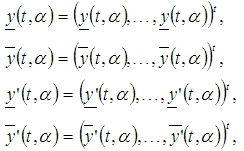 and
and 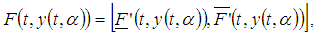 where
where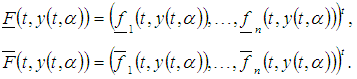 Function
Function 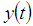 is a fuzzy solution of (3) on an interval
is a fuzzy solution of (3) on an interval 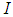 for all
for all 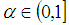 , if
, if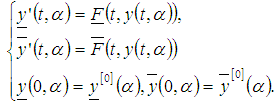 | (4) |
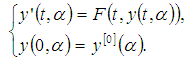 | (5) |
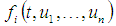 for
for 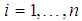 are continuous function of
are continuous function of 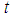 and satisfies the Lipschitz condition in
and satisfies the Lipschitz condition in 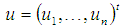 in the region
in the region 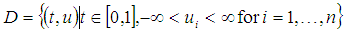 with constant
with constant 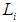 then the initial value problem (2) has unique solution in each case.Proof. See [15]By Theorem 3.1 the initial value problem (2) has a unique solution
then the initial value problem (2) has unique solution in each case.Proof. See [15]By Theorem 3.1 the initial value problem (2) has a unique solution 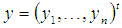 .
.2.3. Runge Kutta Method
- The basis of all Runge Kutta method of order m is to express the difference between the value of
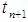 and
and 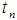 as
as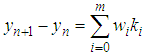 where
where 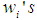 are constants and
are constants and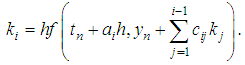 The Runge Kutta method of order 3 based on combination of arithmetic, harmonic and geometric means is [16]
The Runge Kutta method of order 3 based on combination of arithmetic, harmonic and geometric means is [16]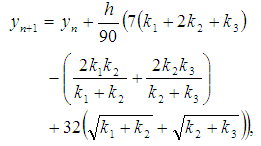 | (6) |
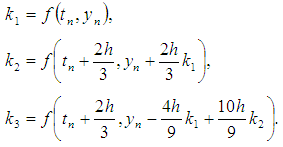
3. The Third Order of Runge Kutta Method Based on Combination of Arithmatics, Harmonics and Geometrics Mean
- Define
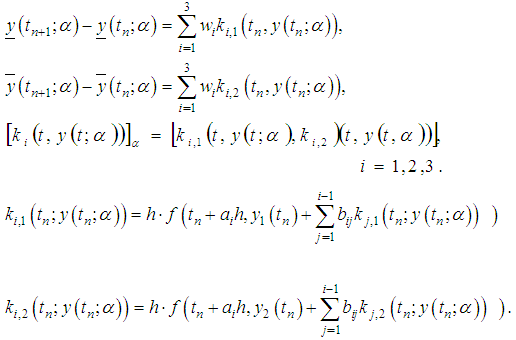 With
With 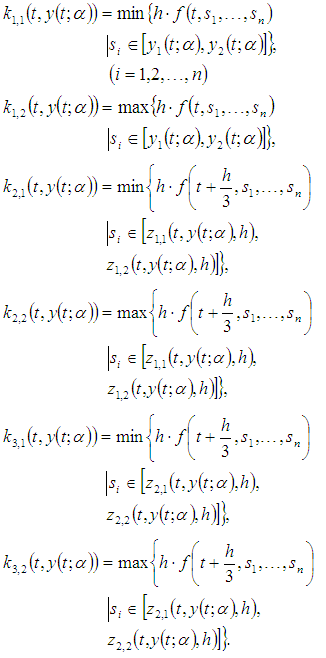 By the third order Runge Kutta based on combination of means, we obtain
By the third order Runge Kutta based on combination of means, we obtain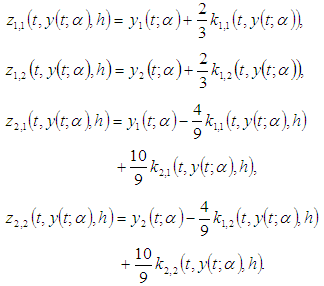 From Eq. (6), define
From Eq. (6), define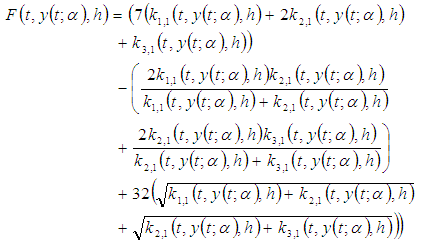 and
and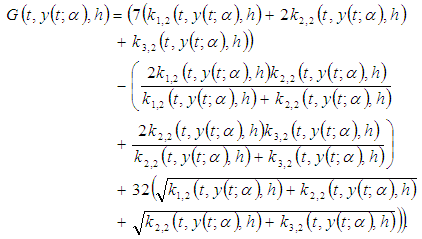 The discrete equally spaced grid points
The discrete equally spaced grid points 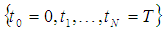 is a partition for interval
is a partition for interval 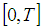 . If the exact and the approximate solution in the i-th
. If the exact and the approximate solution in the i-th 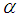 cut at
cut at 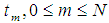 are denoted by
are denoted by 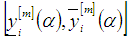 and
and 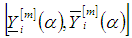 respectively, then the numerical solution by third order Runge Kutta method based on combination of arithmetic, harmonics and geometrics means is
respectively, then the numerical solution by third order Runge Kutta method based on combination of arithmetic, harmonics and geometrics means is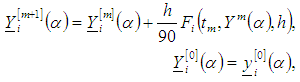
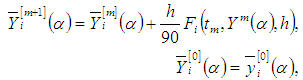
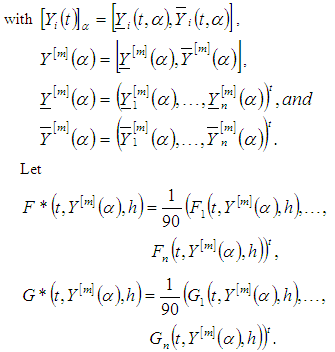 The approximate solution for
The approximate solution for 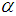 -cut of Eq.(2) is
-cut of Eq.(2) is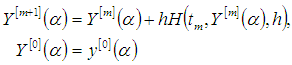 | (7) |
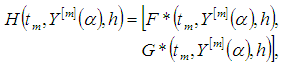 and
and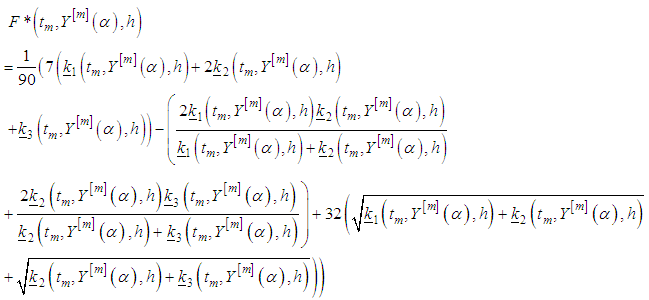
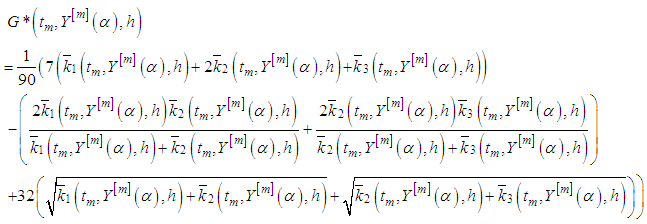 with
with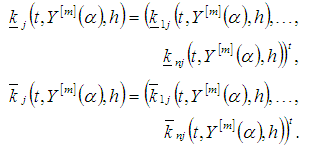
3.1. Stability, Convergence and Error Analysis
- To analyse the stability, convergence and the error of the method, consider the next definition and theorem.Definition 3.1. [15] A one-step method for approximating the solution of differential equation
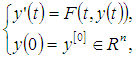 with
with 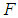 is a
is a 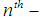 ordered as
ordered as 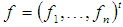 and
and 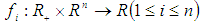 is a method that can be written in the form
is a method that can be written in the form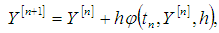 | (8) |
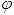 is determined by
is determined by 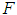 .Theorem 3.2. If
.Theorem 3.2. If 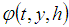 satisfies a Lipschitz condition in
satisfies a Lipschitz condition in 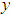 then the method given by (8) is stable.Theorem 3.3. In relation (2), if
then the method given by (8) is stable.Theorem 3.3. In relation (2), if 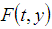 satisfies a Lipschitz condition in y then the method given by (7) is stable.Theorem 3.4. If
satisfies a Lipschitz condition in y then the method given by (7) is stable.Theorem 3.4. If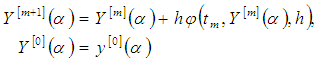 where
where 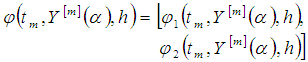 Is a numerical method for approximation of differential equation (2),
Is a numerical method for approximation of differential equation (2), 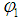 and
and 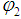 are continuous in
are continuous in 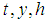 for
for 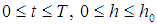 and all
and all 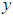 , and if they satisfy a Lipschitz condition in the region
, and if they satisfy a Lipschitz condition in the region 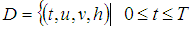 ,
, 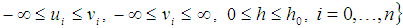 , the necessary and sufficient conditions for convergence is
, the necessary and sufficient conditions for convergence is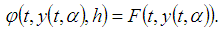 Proof. See [15].Then the method proposed by (6) is convergent to the solution of the system (2).
Proof. See [15].Then the method proposed by (6) is convergent to the solution of the system (2).3.2. Numerical Examples
- The next example show the performance the new method.
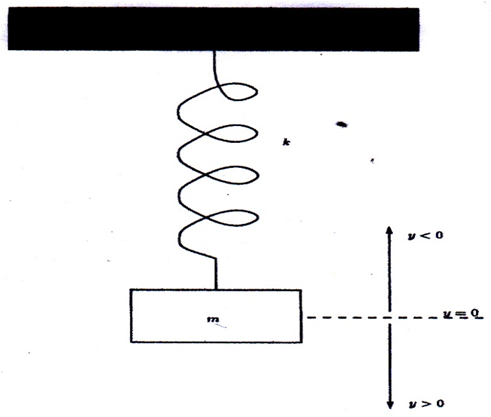 | Figure 1 |
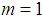 slug) in Fig.1. The spring constant is
slug) in Fig.1. The spring constant is 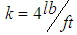 , there is no damping force and the forcing function is
, there is no damping force and the forcing function is 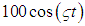 for
for 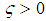 . The differential equation of motion is
. The differential equation of motion is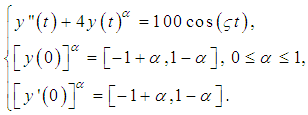 Let
Let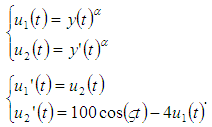 The exact solution is
The exact solution is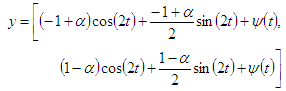 for
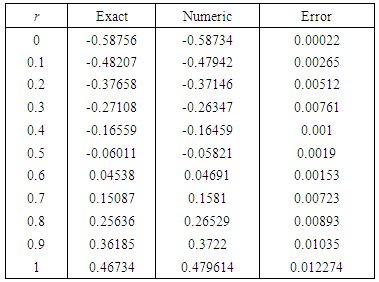
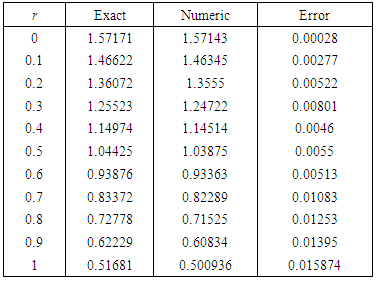
for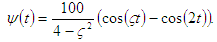 By using the new method, the numerical solution is in Table 1 and Table 2.
By using the new method, the numerical solution is in Table 1 and Table 2.
|
|
4. Conclusions
- In this paper we presented a numerical approach to solve system of fuzzy differential equations with initial value. The scheme is based on the third order Runge Kutta method for solving n-th order of fuzzy initial value probrems. The stability, convergence and error analysis have been studied. Numerical simulation performs that the new method is an accurate method for n-th order of fuzzy initial value problems.
ACKNOWLEDGEMENTS
- This works has fully supported by the Ministry of Research Technology and Higher Education of Indonesia.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML