Sencer Taneri
Private Researcher, Turkey
Correspondence to: Sencer Taneri, Private Researcher, Turkey.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Bosons and Fermions are observable in nature while Quarks appear only in triplets for matter particles. We find a theoretical proof for this statement in this paper by investigating 2-dim model. The occupation numbers q are calculated by a power law dependence of occupation probability and utilizing Hausdorff dimension for the infinitely small mesh in the phase space. The occupation number for Quarks are manipulated and found to be equal to approximately three as they are Parafermions.
Keywords:
Probability and Statistics, Parastatistics, Boson, Fermion, Parafermion, Hausdorff dimension, Percolation, Clusters
Cite this paper: Sencer Taneri, Why Fermions and Bosons are Observable as Single Particles while Quarks are not?, Applied Mathematics, Vol. 8 No. 1, 2018, pp. 5-8. doi: 10.5923/j.am.20180801.02.
1. Introduction
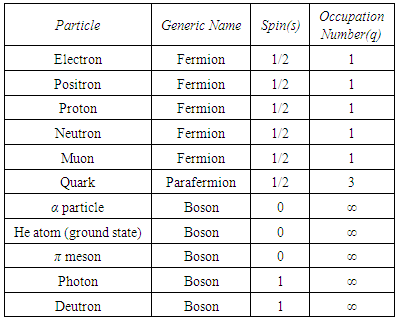
The essential difference in classical and quantum descriptions of N identical particles is in their individuality, rather than in their indistinguishability [1]. Spin of the particle is one of its intrinsic physical quantity that is unique to its individuality. The basis for how the quantum states for N identical particles will be occupied may be taken as experimental, as hypothetical, or as quantum field theoretical, but most probably suggesting a combination of the three is best.There may be particles that obey some kind of statistics, generally called parastatistics. The Parastatistics proposed in 1952 by H. Green was deduced using a quantum field theory (QFT) [2, 3]. Whenever we discover a new particle, it is almost certain that we attribute its behavior to the property that it obeys some form of parastatistics and the maximum occupation number q of a given quantum state would be a finite number that could assume any integer value as 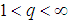 (see Table 1). But, the evident fundamental result is that all particles are either Fermions or Bosons. It is not so clear why we call all particles as either Fermions or Bosons, and this situation may be discovered in this article by consideration of the quantum mechanical quantity spin.
(see Table 1). But, the evident fundamental result is that all particles are either Fermions or Bosons. It is not so clear why we call all particles as either Fermions or Bosons, and this situation may be discovered in this article by consideration of the quantum mechanical quantity spin.Table 1. The Character of Various Particles
 |
| |
|
2. Theory
Particles which are described by anti-symmetric eigenfunctions are called Fermions, and particles which are described by symmetric eigenfunctions are called Bosons in quantum statistics [4]. That is, the eigenfunctions for a system of several identical Fermions switch sign if the labels of any two of them are exchanged, while the eigenfunction for a system of several identical Bosons does not switch sign in such a particle exchange. The symmetry and antisymmetry under the interchange of two particles is a characteristics of the particles, and not something that can be arranged in preparation of the initial state [5-11]. The law, which was discovered by Pauli states that1. Systems consisting of identical particles for half-odd-integral spin (i.e., spin 1/2, 3/2..) are described by antisymmetric wave functions. Such kind of particles are called Fermions and are said to obey Fermi-Dirac statistics.2. Systems consisting of identical spin (spin 0,1,2,..) are described by symmetric wave functions. Such kind of particles are called Bosons, and are said to obey Bose-Einstein statistics.In 1964, Gell-Mann and Feynmann's PhD student George Zweig, who was working at CERN, proposed that baryons and mesons are bound states of hypothetical triplet particles. Gell-Mann called the triplet particles "quarks", using a word that had been introduced by James Joyce in his novel Finnegans Wake [12].In order to understand the statistics of a particle, it is useful to assemble a collection of them. Then, one can find the maximum number that can occur in completely symmetric or antisymmetric states. It is known that when no more than q particles can exist in any completely antisymmetric (symmetric) state, the particles are called Parafermions (Parabosons) of order q. Ohnuki e Kamefuchi analyzed the possibility of quarks be Parafermions, as proposed by Greenberg in 1964 [13, 14]. The conclusion was that the quarks cinematic properties obeying the parafermionic statistics can not explain the quark confinement by themselves and that the para-quark model is compatible with the SU(3)c color gauge. Here, we set up a theoretical construction in the next section to observe the parastatistics of matter particles.
3. Model
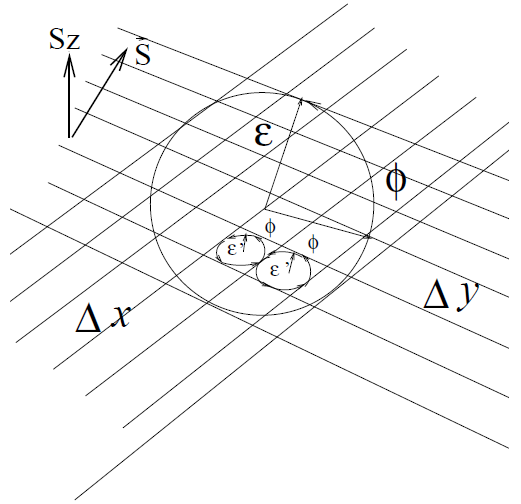 | Figure 1. Infinitesimally small mesh in phase space with edges 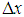 and and 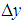 yet divided into twice infinitesimally smaller meshes. yet divided into twice infinitesimally smaller meshes. 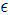 and and 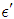 are radii of the circles while are radii of the circles while 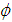 phase angle is same for both radii. phase angle is same for both radii. 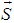 whose z component whose z component 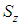 is perpendicular to both of is perpendicular to both of 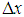 and and 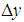 , is the spin vector of the cluster , is the spin vector of the cluster |
We see infinitesimally small mesh in space with edges having uncertainty in position 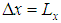 and position
and position 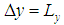 in Fig. 1. Let this small mesh contain an electron cluster rotating with spin
in Fig. 1. Let this small mesh contain an electron cluster rotating with spin 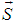 and occupation number q . The mesh can still be divided into infinitesimally smaller segments where matter percolates in 2-dim till it reaches the exterior edges of
and occupation number q . The mesh can still be divided into infinitesimally smaller segments where matter percolates in 2-dim till it reaches the exterior edges of 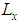 and
and 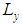 where it is called a cluster now. Let P the probability that spin
where it is called a cluster now. Let P the probability that spin 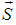 cluster with mass M occupies an area A and traces an arc of phase angle
cluster with mass M occupies an area A and traces an arc of phase angle 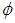 and radius
and radius 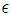 while being at the boundaries of a drum to which twice infinitesimally small meshes with edges
while being at the boundaries of a drum to which twice infinitesimally small meshes with edges 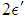 belong in space. If
belong in space. If 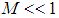 and
and 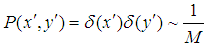 , one can write for the probability P that the smaller meshes at the origin are occupied for isotropic space,
, one can write for the probability P that the smaller meshes at the origin are occupied for isotropic space,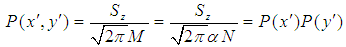 | (1) |
where 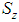 is the magnitude of z component of spin vector
is the magnitude of z component of spin vector 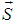 to take spin degeneracy into account and N is number of occupied sites. Further by mass action law in percolation theory,
to take spin degeneracy into account and N is number of occupied sites. Further by mass action law in percolation theory, 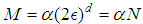 is valid for big circle composed of smaller sites in 2-dim. Here,
is valid for big circle composed of smaller sites in 2-dim. Here, 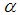 is some proportionality constant and d is dimension of the cluster [15]. Percolation theory forms the basis of the liquid dynamics of the lepton liquid problem for electron. Returning to equation (1) for
is some proportionality constant and d is dimension of the cluster [15]. Percolation theory forms the basis of the liquid dynamics of the lepton liquid problem for electron. Returning to equation (1) for 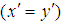 , we set the probabilities,
, we set the probabilities,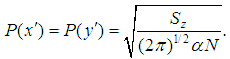 | (2) |
Then, one can write the probability for the small mesh,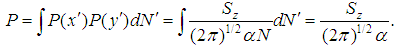 | (3) |
If 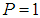 then
then 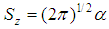 where
where 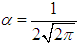 is the concentration density of the lepton liquid in the electron with
is the concentration density of the lepton liquid in the electron with 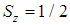 . Conclusively, equation (2) becomes
. Conclusively, equation (2) becomes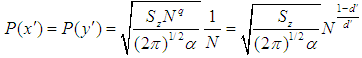 | (4) |
where 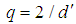 is the occupation number equal to 1 for the electron and d' is dimension equal to 2 as well. Further, mass M equals
is the occupation number equal to 1 for the electron and d' is dimension equal to 2 as well. Further, mass M equals 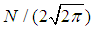 , number of occupied sites
, number of occupied sites 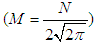 . The spectral probability P' (spectral density, with exponential time dependence (traveling wave solution)) is the Gamma function integral [16] which yields following with convolution of Faltung theorem [17] for very large
. The spectral probability P' (spectral density, with exponential time dependence (traveling wave solution)) is the Gamma function integral [16] which yields following with convolution of Faltung theorem [17] for very large 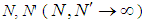 ,
,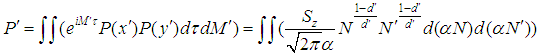 | (5) |
where 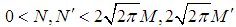 . This is nothing but,
. This is nothing but,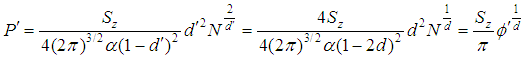 | (6) |
where 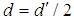 and
and 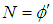 where
where 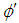 is the phase angle, are purely empirical in Fig. 1. Here, electrons are Fermions with
is the phase angle, are purely empirical in Fig. 1. Here, electrons are Fermions with 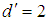 and
and 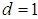 , and thus with
, and thus with 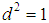 and occupation number
and occupation number 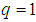 . This yields a number for P' which may be larger than one as the numerator is some number on the Riemann surface. We make the transformation
. This yields a number for P' which may be larger than one as the numerator is some number on the Riemann surface. We make the transformation 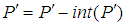 with
with 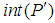 , integer value of P' in order to have
, integer value of P' in order to have 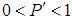 and to have the numerator equals some number between 0 and
and to have the numerator equals some number between 0 and 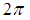 with branch cut at
with branch cut at 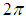 . So,
. So, 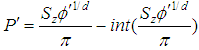 | (7) |
is the final form of the formula for the spectral probability for the infinitesimally small mesh with sides 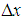 and
and 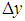 , see Fig. 1. Note that, due to equation (7) and simple geometric arguments, this spectral probability P' (ensemble average probability) is equal to occupation probability of matter
, see Fig. 1. Note that, due to equation (7) and simple geometric arguments, this spectral probability P' (ensemble average probability) is equal to occupation probability of matter  (time average probability) in twice infinitesimally small mesh with radius
(time average probability) in twice infinitesimally small mesh with radius 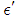 to be analyzed in the next paragraph
to be analyzed in the next paragraph 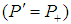 (Stationary Ergodic Theorem).Now, we make the connection between probability P' and dimension d again by utilizing the fractal theory. First, one should denote that there are two probabilities for the matter (for two states + and -) in space, the probability
(Stationary Ergodic Theorem).Now, we make the connection between probability P' and dimension d again by utilizing the fractal theory. First, one should denote that there are two probabilities for the matter (for two states + and -) in space, the probability 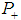 that twice infinitesimally smaller mesh is occupied and the probability
that twice infinitesimally smaller mesh is occupied and the probability 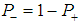 that it is empty. Moreover, this probability is equal to percolation probability of matter to neighboring sites in 1-dim. Second, one recalls the Hausdorff dimension is defined as follows [18, 19]. Given probability distribution
that it is empty. Moreover, this probability is equal to percolation probability of matter to neighboring sites in 1-dim. Second, one recalls the Hausdorff dimension is defined as follows [18, 19]. Given probability distribution 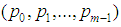 with
with 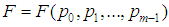 , we define
, we define | (8) |
as the Hausdorff dimension for clusters. Note that we have two states of elements, 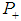 and
and 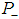 . If this dimension is equal to the dimension d in equation (7), one can obtain,
. If this dimension is equal to the dimension d in equation (7), one can obtain,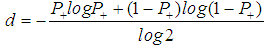 | (9) |
where,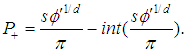 | (10) |
So, given the spin of the cluster s, we have two unknowns, the phase 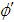 and dimension d.
and dimension d.
4. Results and Discussion
Our calculation here reminds techniques of self consistent solution of the method above. Equation set (9-10) have self consistent trivial solutions;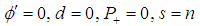 | (11) |
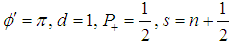 | (12) |
for spin s and integer 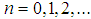 . The occupation number mentioned in Theory section may be taken as
. The occupation number mentioned in Theory section may be taken as 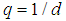 and the results may be summarized as,
and the results may be summarized as,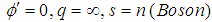 | (13) |
 | (14) |
This means Bosons are points and Fermions are lines in this space. We can implement infinitely many Bosons to the same state and only one Fermion can occupy a given state.The self consistent nontrivial solution is the,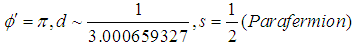 | (15) |
solution which yields 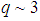 the Parafermion solution for Quarks! More precisely, we observe Quarks as triplets (as in protons, neutrons, etc.) not as single particles because they form clusters with dimension
the Parafermion solution for Quarks! More precisely, we observe Quarks as triplets (as in protons, neutrons, etc.) not as single particles because they form clusters with dimension 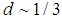 except for two cases. First case is meson wherein quark and anti-quark (as anti-matter) pair is involved. Second case is 5 quarks which is a composition of four quarks and an anti-strange quark. In 2003 came experimental evidence of the five quark combination which is being called the penta-quark. Strong evidence for the penta-quark came from experiments in Jefferson Lab in Newport News, Virginia during that year [20].Other choices for the effect of parity operator
except for two cases. First case is meson wherein quark and anti-quark (as anti-matter) pair is involved. Second case is 5 quarks which is a composition of four quarks and an anti-strange quark. In 2003 came experimental evidence of the five quark combination which is being called the penta-quark. Strong evidence for the penta-quark came from experiments in Jefferson Lab in Newport News, Virginia during that year [20].Other choices for the effect of parity operator 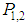 appear in some theories of fractional quantum Hall effect, high temperature superconductivity, and some quark models. Sometimes, the distinction between Bosons and Fermions disappears, and the properties of superconductors are inherently present in two dimensions. In such situations, the consequences of
appear in some theories of fractional quantum Hall effect, high temperature superconductivity, and some quark models. Sometimes, the distinction between Bosons and Fermions disappears, and the properties of superconductors are inherently present in two dimensions. In such situations, the consequences of  have been explored extensively for values of
have been explored extensively for values of 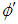 other than 0 and
other than 0 and 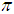 . The resulting states are called anyons; when they are
. The resulting states are called anyons; when they are 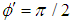 , they are called semions for such values.We can use occupation number
, they are called semions for such values.We can use occupation number 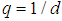 to summarize our result for the probability as,
to summarize our result for the probability as,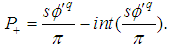 | (16) |
which reminds us the results of renormalization theory.
5. Conclusions
We conclude that we are able to observe clusters with dimension d being equal to a natural number (i.e. 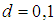 .) as single particles. We can observe infinitely many Bosons in the same state and can observe only one Fermion at a given state. Other solutions for the dimension (not being natural numbers) are clusters and can not be observed as single particles such as quarks (i.e.
.) as single particles. We can observe infinitely many Bosons in the same state and can observe only one Fermion at a given state. Other solutions for the dimension (not being natural numbers) are clusters and can not be observed as single particles such as quarks (i.e. 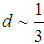 ). Such cluster models with Hausdorff dimension calculations are also used in evolution as the quasi-species explore the genetic phase space and thereby adapt to new environmental conditions.There is a strong tendency in conventional and non-conventional statistics that the real particles can only be bosons and fermions and that all other particles, different from bosons and fermions, would be quasi-particles. Only bosons and fermions are detected in 3-dim systems and quasi-particles called anyons which have charge and spin fractionary are detected in 2-dim systems. So, quarks with fractionary charge and spin are quasi-particles (collective excitations"). Since they are anyons
). Such cluster models with Hausdorff dimension calculations are also used in evolution as the quasi-species explore the genetic phase space and thereby adapt to new environmental conditions.There is a strong tendency in conventional and non-conventional statistics that the real particles can only be bosons and fermions and that all other particles, different from bosons and fermions, would be quasi-particles. Only bosons and fermions are detected in 3-dim systems and quasi-particles called anyons which have charge and spin fractionary are detected in 2-dim systems. So, quarks with fractionary charge and spin are quasi-particles (collective excitations"). Since they are anyons 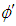 may be a little less than
may be a little less than  and occupation number q may be exactly equal to 3
and occupation number q may be exactly equal to 3 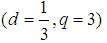 in equation (15).Other methods for calculation of intrinsic spin values and occupation numbers for Fermions, Bosons and Quarks should rather involve the usage of more advanced tools such as quantum field theory [21]. Our scope here may be more shallow with respect to quantum chromodynamics theory methods first proved in 1973 [22]. In that year, the concept of colour as the source of a "strong field" was developed into the theory of QCD by European physicists Harald Fritzsch and Heinrich Leutwyler, together with American physicist Murray Gell-Mann. In particular, they employed the general field theory developed in 1950s by Chen Ning Yang and Robert Mills. However, the purpose of answering the question in title of this paper is well achieved by utilizing percolation theory and cluster models.
in equation (15).Other methods for calculation of intrinsic spin values and occupation numbers for Fermions, Bosons and Quarks should rather involve the usage of more advanced tools such as quantum field theory [21]. Our scope here may be more shallow with respect to quantum chromodynamics theory methods first proved in 1973 [22]. In that year, the concept of colour as the source of a "strong field" was developed into the theory of QCD by European physicists Harald Fritzsch and Heinrich Leutwyler, together with American physicist Murray Gell-Mann. In particular, they employed the general field theory developed in 1950s by Chen Ning Yang and Robert Mills. However, the purpose of answering the question in title of this paper is well achieved by utilizing percolation theory and cluster models.
ACKNOWLEDGMENTS
The author would like to thank Prof.Dr. Cemsinan Deliduman from MSU in Turkey for critical reading of the manuscript.
References
| [1] | H.S. Robertson, Stat. Thermophys., p.168,496,497 (Prentice-Hall Inc.,1993). |
| [2] | M. Cattani and J.M.F. Bassalo, http://arxiv.org/ftp/arxiv/papers/0903/0903.4773.pdf. |
| [3] | H.S. Green. Phys.Rev.90, 270 (1953). |
| [4] | R. Eisberg, R. Resnick, Quantum Physics, p.378, (John Wiley Sons, 1985). |
| [5] | S. Gasiorowicz, Quantum Physics, p.148 (John Wiley Sons, 1974). |
| [6] | R. Shankar, Princ. of Quantum. Mech., p.272 (Plenum Press, NY, 1980). |
| [7] | J.J. Sakurai, Mod. Quantum Mech., p.361 (Addison-Wisley Publ. Comp., 1994). |
| [8] | K. Huang, Stat. Mech., p.241-278, (John Wiley Sons, 1987). |
| [9] | F. Reif, Stat. and Therm. Phys., pp.346-350, (McGraw-Hill Book Comp., 1965). |
| [10] | C. Kittel, Int. Solid State Phys., p.130, (John Wiley Sons, 1986). |
| [11] | F. Halzen, A.D. Martin, Quarks and Leptons: An Int. Cour. in Mod. Part. Phys., p.2 (John Wiley Sons, 1984). |
| [12] | http://cerncourier.com/cws/article/cern/50796. |
| [13] | Y. Ohnuki and S. Kamefuchi, "Quatum Filed Theory and Parastatistics". Springer-Verlag (1990). |
| [14] | O.W. Greenberg, Phys.Rev.Lett.598 (1964). |
| [15] | S. Taneri, Eur. Phys. J. B, 47 (2005) 417-422. |
| [16] | M. Lapidus, G. Radinovic, D. Zubrinic, "Fractal Zeta Functions and Fractal Drums", Springer Mono. in Math. (2016). |
| [17] | G. Arfken, Math. Meth. for Phys., p.811,849,850, (1985). |
| [18] | S. Taneri, Mod. Phys. Lett. B, 26, 26, (2012), 1250169. |
| [19] | K.J. Falconer, Fractal Geometry Mathematical Foundations and Applications (John Wiley, New York, 2003), p.152. |
| [20] | hyperphysics.phy-astr.gsu.edu/hbase/particles/pquark.html#c/. |
| [21] | S. Weinberg, Quantum Theory of Fields (University of Cambridge, 1995), Vol.1, pp.233-238, Vol.2, p.152. |
| [22] | https://www.britannica.com/science/quantum-chromodynamics. |


 (see Table 1). But, the evident fundamental result is that all particles are either Fermions or Bosons. It is not so clear why we call all particles as either Fermions or Bosons, and this situation may be discovered in this article by consideration of the quantum mechanical quantity spin.
(see Table 1). But, the evident fundamental result is that all particles are either Fermions or Bosons. It is not so clear why we call all particles as either Fermions or Bosons, and this situation may be discovered in this article by consideration of the quantum mechanical quantity spin.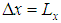 and position
and position 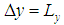 in Fig. 1. Let this small mesh contain an electron cluster rotating with spin
in Fig. 1. Let this small mesh contain an electron cluster rotating with spin 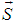 and occupation number q . The mesh can still be divided into infinitesimally smaller segments where matter percolates in 2-dim till it reaches the exterior edges of
and occupation number q . The mesh can still be divided into infinitesimally smaller segments where matter percolates in 2-dim till it reaches the exterior edges of 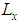 and
and 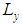 where it is called a cluster now. Let P the probability that spin
where it is called a cluster now. Let P the probability that spin 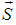 cluster with mass M occupies an area A and traces an arc of phase angle
cluster with mass M occupies an area A and traces an arc of phase angle 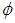 and radius
and radius 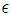 while being at the boundaries of a drum to which twice infinitesimally small meshes with edges
while being at the boundaries of a drum to which twice infinitesimally small meshes with edges 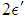 belong in space. If
belong in space. If 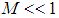 and
and 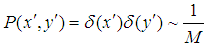 , one can write for the probability P that the smaller meshes at the origin are occupied for isotropic space,
, one can write for the probability P that the smaller meshes at the origin are occupied for isotropic space,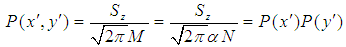
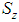 is the magnitude of z component of spin vector
is the magnitude of z component of spin vector 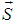 to take spin degeneracy into account and N is number of occupied sites. Further by mass action law in percolation theory,
to take spin degeneracy into account and N is number of occupied sites. Further by mass action law in percolation theory, 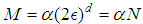 is valid for big circle composed of smaller sites in 2-dim. Here,
is valid for big circle composed of smaller sites in 2-dim. Here, 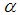 is some proportionality constant and d is dimension of the cluster [15]. Percolation theory forms the basis of the liquid dynamics of the lepton liquid problem for electron. Returning to equation (1) for
is some proportionality constant and d is dimension of the cluster [15]. Percolation theory forms the basis of the liquid dynamics of the lepton liquid problem for electron. Returning to equation (1) for 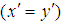 , we set the probabilities,
, we set the probabilities,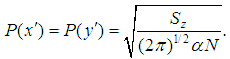
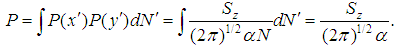
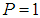 then
then 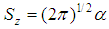 where
where 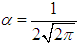 is the concentration density of the lepton liquid in the electron with
is the concentration density of the lepton liquid in the electron with 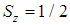 . Conclusively, equation (2) becomes
. Conclusively, equation (2) becomes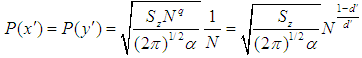
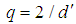 is the occupation number equal to 1 for the electron and d' is dimension equal to 2 as well. Further, mass M equals
is the occupation number equal to 1 for the electron and d' is dimension equal to 2 as well. Further, mass M equals 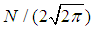 , number of occupied sites
, number of occupied sites 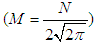 . The spectral probability P' (spectral density, with exponential time dependence (traveling wave solution)) is the Gamma function integral [16] which yields following with convolution of Faltung theorem [17] for very large
. The spectral probability P' (spectral density, with exponential time dependence (traveling wave solution)) is the Gamma function integral [16] which yields following with convolution of Faltung theorem [17] for very large 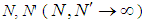 ,
,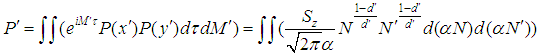
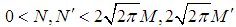 . This is nothing but,
. This is nothing but,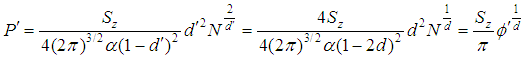
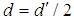 and
and 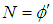 where
where 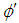 is the phase angle, are purely empirical in Fig. 1. Here, electrons are Fermions with
is the phase angle, are purely empirical in Fig. 1. Here, electrons are Fermions with 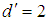 and
and 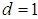 , and thus with
, and thus with 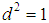 and occupation number
and occupation number 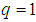 . This yields a number for P' which may be larger than one as the numerator is some number on the Riemann surface. We make the transformation
. This yields a number for P' which may be larger than one as the numerator is some number on the Riemann surface. We make the transformation 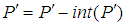 with
with 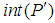 , integer value of P' in order to have
, integer value of P' in order to have 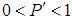 and to have the numerator equals some number between 0 and
and to have the numerator equals some number between 0 and 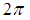 with branch cut at
with branch cut at 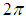 . So,
. So, 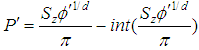
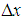 and
and 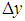 , see Fig. 1. Note that, due to equation (7) and simple geometric arguments, this spectral probability P' (ensemble average probability) is equal to occupation probability of matter
, see Fig. 1. Note that, due to equation (7) and simple geometric arguments, this spectral probability P' (ensemble average probability) is equal to occupation probability of matter 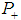 (time average probability) in twice infinitesimally small mesh with radius
(time average probability) in twice infinitesimally small mesh with radius 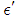 to be analyzed in the next paragraph
to be analyzed in the next paragraph 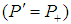 (Stationary Ergodic Theorem).Now, we make the connection between probability P' and dimension d again by utilizing the fractal theory. First, one should denote that there are two probabilities for the matter (for two states + and -) in space, the probability
(Stationary Ergodic Theorem).Now, we make the connection between probability P' and dimension d again by utilizing the fractal theory. First, one should denote that there are two probabilities for the matter (for two states + and -) in space, the probability 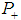 that twice infinitesimally smaller mesh is occupied and the probability
that twice infinitesimally smaller mesh is occupied and the probability 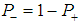 that it is empty. Moreover, this probability is equal to percolation probability of matter to neighboring sites in 1-dim. Second, one recalls the Hausdorff dimension is defined as follows [18, 19]. Given probability distribution
that it is empty. Moreover, this probability is equal to percolation probability of matter to neighboring sites in 1-dim. Second, one recalls the Hausdorff dimension is defined as follows [18, 19]. Given probability distribution 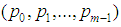 with
with 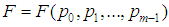 , we define
, we define
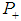 and
and 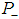 . If this dimension is equal to the dimension d in equation (7), one can obtain,
. If this dimension is equal to the dimension d in equation (7), one can obtain,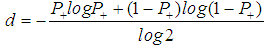
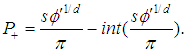
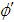 and dimension d.
and dimension d.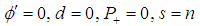
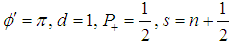
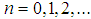 . The occupation number mentioned in Theory section may be taken as
. The occupation number mentioned in Theory section may be taken as 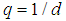 and the results may be summarized as,
and the results may be summarized as,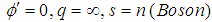

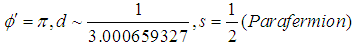
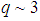 the Parafermion solution for Quarks! More precisely, we observe Quarks as triplets (as in protons, neutrons, etc.) not as single particles because they form clusters with dimension
the Parafermion solution for Quarks! More precisely, we observe Quarks as triplets (as in protons, neutrons, etc.) not as single particles because they form clusters with dimension 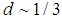 except for two cases. First case is meson wherein quark and anti-quark (as anti-matter) pair is involved. Second case is 5 quarks which is a composition of four quarks and an anti-strange quark. In 2003 came experimental evidence of the five quark combination which is being called the penta-quark. Strong evidence for the penta-quark came from experiments in Jefferson Lab in Newport News, Virginia during that year [20].Other choices for the effect of parity operator
except for two cases. First case is meson wherein quark and anti-quark (as anti-matter) pair is involved. Second case is 5 quarks which is a composition of four quarks and an anti-strange quark. In 2003 came experimental evidence of the five quark combination which is being called the penta-quark. Strong evidence for the penta-quark came from experiments in Jefferson Lab in Newport News, Virginia during that year [20].Other choices for the effect of parity operator 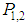 appear in some theories of fractional quantum Hall effect, high temperature superconductivity, and some quark models. Sometimes, the distinction between Bosons and Fermions disappears, and the properties of superconductors are inherently present in two dimensions. In such situations, the consequences of
appear in some theories of fractional quantum Hall effect, high temperature superconductivity, and some quark models. Sometimes, the distinction between Bosons and Fermions disappears, and the properties of superconductors are inherently present in two dimensions. In such situations, the consequences of  have been explored extensively for values of
have been explored extensively for values of 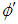 other than 0 and
other than 0 and 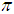 . The resulting states are called anyons; when they are
. The resulting states are called anyons; when they are 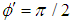 , they are called semions for such values.We can use occupation number
, they are called semions for such values.We can use occupation number 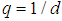 to summarize our result for the probability as,
to summarize our result for the probability as,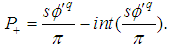
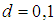 .) as single particles. We can observe infinitely many Bosons in the same state and can observe only one Fermion at a given state. Other solutions for the dimension (not being natural numbers) are clusters and can not be observed as single particles such as quarks (i.e.
.) as single particles. We can observe infinitely many Bosons in the same state and can observe only one Fermion at a given state. Other solutions for the dimension (not being natural numbers) are clusters and can not be observed as single particles such as quarks (i.e. 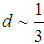 ). Such cluster models with Hausdorff dimension calculations are also used in evolution as the quasi-species explore the genetic phase space and thereby adapt to new environmental conditions.There is a strong tendency in conventional and non-conventional statistics that the real particles can only be bosons and fermions and that all other particles, different from bosons and fermions, would be quasi-particles. Only bosons and fermions are detected in 3-dim systems and quasi-particles called anyons which have charge and spin fractionary are detected in 2-dim systems. So, quarks with fractionary charge and spin are quasi-particles (collective excitations"). Since they are anyons
). Such cluster models with Hausdorff dimension calculations are also used in evolution as the quasi-species explore the genetic phase space and thereby adapt to new environmental conditions.There is a strong tendency in conventional and non-conventional statistics that the real particles can only be bosons and fermions and that all other particles, different from bosons and fermions, would be quasi-particles. Only bosons and fermions are detected in 3-dim systems and quasi-particles called anyons which have charge and spin fractionary are detected in 2-dim systems. So, quarks with fractionary charge and spin are quasi-particles (collective excitations"). Since they are anyons 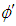 may be a little less than
may be a little less than 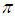 and occupation number q may be exactly equal to 3
and occupation number q may be exactly equal to 3 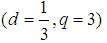 in equation (15).Other methods for calculation of intrinsic spin values and occupation numbers for Fermions, Bosons and Quarks should rather involve the usage of more advanced tools such as quantum field theory [21]. Our scope here may be more shallow with respect to quantum chromodynamics theory methods first proved in 1973 [22]. In that year, the concept of colour as the source of a "strong field" was developed into the theory of QCD by European physicists Harald Fritzsch and Heinrich Leutwyler, together with American physicist Murray Gell-Mann. In particular, they employed the general field theory developed in 1950s by Chen Ning Yang and Robert Mills. However, the purpose of answering the question in title of this paper is well achieved by utilizing percolation theory and cluster models.
in equation (15).Other methods for calculation of intrinsic spin values and occupation numbers for Fermions, Bosons and Quarks should rather involve the usage of more advanced tools such as quantum field theory [21]. Our scope here may be more shallow with respect to quantum chromodynamics theory methods first proved in 1973 [22]. In that year, the concept of colour as the source of a "strong field" was developed into the theory of QCD by European physicists Harald Fritzsch and Heinrich Leutwyler, together with American physicist Murray Gell-Mann. In particular, they employed the general field theory developed in 1950s by Chen Ning Yang and Robert Mills. However, the purpose of answering the question in title of this paper is well achieved by utilizing percolation theory and cluster models. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

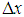 and
and 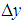 yet divided into twice infinitesimally smaller meshes.
yet divided into twice infinitesimally smaller meshes. 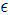 and
and 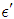 are radii of the circles while
are radii of the circles while 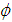 phase angle is same for both radii.
phase angle is same for both radii. 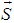 whose z component
whose z component 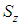 is perpendicular to both of
is perpendicular to both of 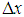 and
and 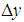 , is the spin vector of the cluster
, is the spin vector of the cluster