-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2017; 7(4): 67-71
doi:10.5923/j.am.20170704.01

The Importance of Radii of Circles in the Determination of Tangents, Homothetic Points and Radical Points/Axis in Two Circle Systems: A Review with Update
Ohochuku N. Stephen
Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Port Harcourt, Nigeria
Correspondence to: Ohochuku N. Stephen, Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

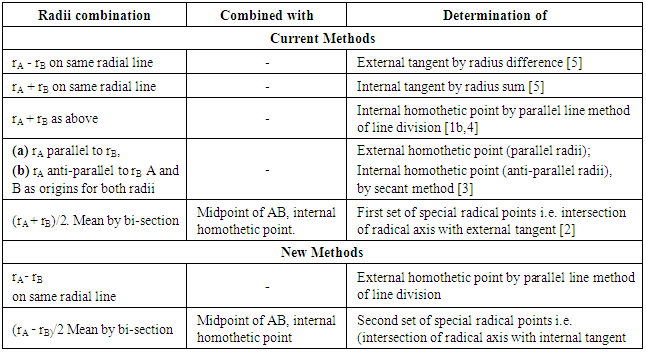
This article brings together the various current procedures used to construct the tangents (common or equal) to the two circles in a two circle system, radical points/axis and homothetic points that are essential to these constructions with the aim of showing the important contributions of the radii of the circles in these operations. Two new methods one for constructing external homothetic point and the other for a pair of special radical points using combinations of the radii are also added as update. All the methods listed show that the radii of the two circles combined in different ways can be used to determine respectively the external homothetic point and the radical points/axis which are essential in the construction of tangents in two circle systems.
Keywords: Circles radii, Tangent, Radical axis/point, Homothetic point
Cite this paper: Ohochuku N. Stephen, The Importance of Radii of Circles in the Determination of Tangents, Homothetic Points and Radical Points/Axis in Two Circle Systems: A Review with Update, Applied Mathematics, Vol. 7 No. 4, 2017, pp. 67-71. doi: 10.5923/j.am.20170704.01.
Article Outline
1. Introduction
- A two circle system is comprised of only two circles. Of all the various two circle systems only the systems in which the circles are of unequal radii or touching externally (i.e. the tangential point is between the centres of the touching circles) or intersecting or isolated are the ones referred to here, figure 1.
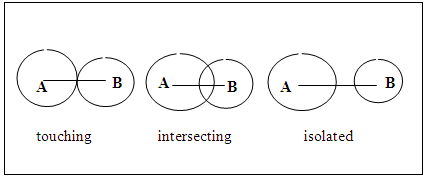 | Figure 1. Illustrating touching, intersecting and isolated circles |
1.1. Tangent to Two Circles
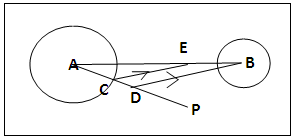
- A tangent to a circle is a straight line drawn from an external point P to touch the circle at a point on its circumference [1], figure 2a. There is an alternative definition [2], both definitions show that the tangential straight line is perpendicular to the radius at its (radius) terminal at the circle’s circumference.
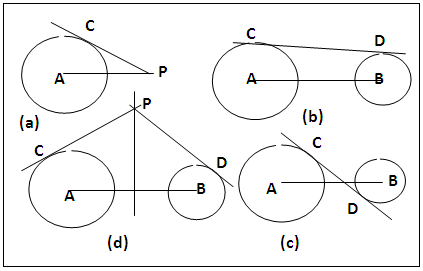 | Figure 2. Illustrations of tangents to circles |
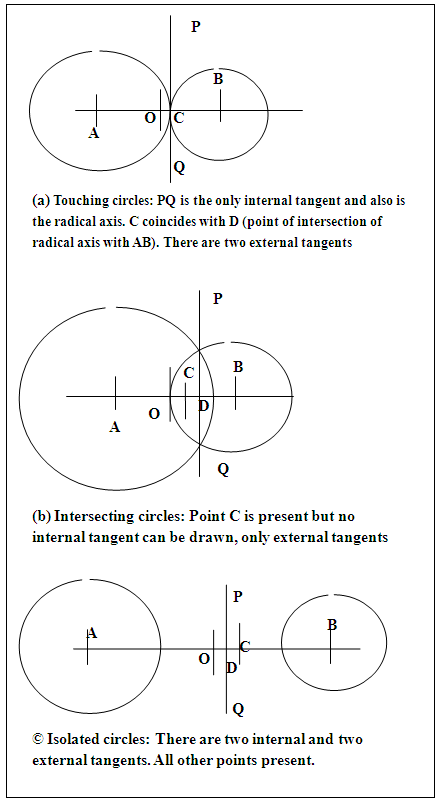 | Figure 3. Relative positions of Internal Homothetic point C, Radical axis PQ, and midpoint O of AB in Systems of Two Circles |
1.2. Common Tangents to Two Circles
- A straight line that touches a point each on the circumference of each circle is a common tangent. There are two pairs of such tangents viz the external tangents CD figure 2b (only one shown) and internal tangents CD, figure 2c (only one shown). The point from which the external tangent is drawn to the circles is the external homothetic point and the point from which the internal tangent is drawn to the circles is the internal homothetic point. These points are determined using the radii of the circles [1b,3].
1.3. Equal Tangents to Two Circles: Radical Axis/Points
- As in figure 2d, equal tangents to each circle can be drawn from an external point P. The point, P, is called a radical point and is one of the numerous linear points from which equal tangents can be drawn to the two circles. The straight line formed by the linear points is the radical axis and it is perpendicular to the line of centres, AB. A pair of radical points called special radical points can be determined using the radii of the circles with other functions of the two circle system [2, 4]. From this special radical point, the external tangent can be drawn and the two equal tangents from this special radical point form a straight line which is the same as the common tangent [4]. The radical axis or radical points can be determined using the radii of the circles with other functions of the two circle system [4].
1.4. Aim of the Work
- From what is said above it is obvious that the radii of the circles play important part in the construction of tangents, radical axis and also homothetic and radical points that are essential to drawing tangent (common or equal) in two circle system. The aim of this article is to assemble the various current methods used to construct tangents, homothetic and radical axis in two circle systems and to investigate the possibility of using the radii in constructing other characteristics of two circle systems such as external homothetic point by parallel line method and the second set of special radical points. The outcome is what is given below after briefly showing the current methods in use to determine homothetic and radical points and the tangents.
2. Methodology
2.1. Summary of Current Methods
2.1.1. Determination of Homothetic Points by Secant Method, Figure 4 [3]
- The circles A and B are drawn as specified; their centres A and B joined and produced both ways, figure 4. Angle 60o is drawn at point A on BA produced to cut circle A at C and also at point B along BA to cut circle B at D and DB is produced to cut circle B at E. CD joined and produced cuts AB produced at F, the external homothetic point. CE joined cuts AB at G the internal homothetic point.
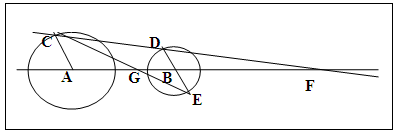 | Figure 4. Illustrating Secant Method of determining External and Internal Homothetic points |
2.1.2. Determination of Internal Homothetic Point by Parallel Line Method of Division of AB
- The circles, A and B, are drawn as specified, their centres A and B joined, figure 5. AP is drawn at convenient inclination to AB and it cuts circle A at C. Centre C, radius rB AP is cut at D. D is joined to B. Through C a straight line parallel to DB is drawn to cut AB at E the internal homothetic point [1b].
 | Figure 5. Illustration of Parallel Line Method of Locating Internal Homothetic Point |
2.1.3. Determination of first set of Special Radical Points and Radical Axis, Figure 6 [2]
- The first set of special radical points is the set of two points of intersections of the radical axis and the two external common tangents.The circles A and B are drawn as specified; their centres A and B joined, figure 6. O is the midpoint of AB and G is the internal homothetic centre determined as in section 2.1.1 or 2.1.2. The mean radius (rA + rB)/2 is determined by bisection. Centre O, with radius as the mean radius arcs are described above and below AB. Centre G and same radius the arcs are cut at R and S. R and S are the pair of special radical points: R and S joined and produced both ways give the radical axis.
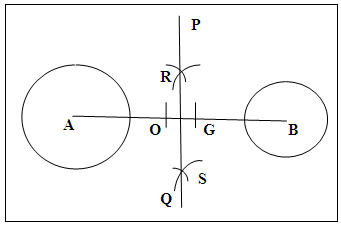 | Figure 6. Determination of Special Radical point and Radical Axis |
2.1.4. Drawing External Tangent to two Circles by the Radius Difference Method, Figure 7
- The Circles A and B are drawn as specified; their centres A and B joined, figure 7 with the lettering. Centre C with radius rB, CA is cut at D. Centre A, radius AD, the dotted circle is drawn. BE is drawn tangential to dotted circle at E. AE is joined and produced to cut circle A at F and FG is drawn parallel to EB as the external tangent [5].
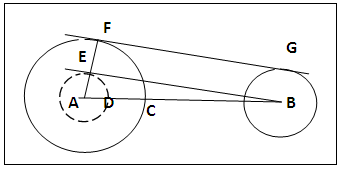 | Figure 7. External tangent by radius difference |
2.1.5. Drawing External Tangent to Two Circles from the Special Radical Point, Figure 8 [2]
- The circles are drawn as specified, figure 8. The mean radius (rA + rB)/2, the midpoint O of AB and G, the internal homothetic point, are determined by any convenient methods. Centre O, with radius as the mean radius swing an arc above AB. Centre G, same radius cut the arc at R. R is one of the special radical points from which a common tangent is drawn to both circles applying the method of drawing tangent to a single circle from an external point.
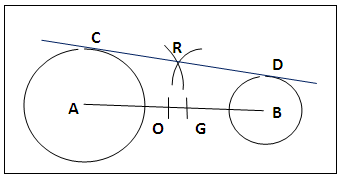 | Figure 8. Drawing External Tangent to two Circles from the special radical point |
2.1.6. Determination of Internal Tangent by the Sum of Radii, Figure 9
- Circles A and B are drawn as specified; their centres A and B joined, figure 9 with the lettering. Centre A, radius rA + rB, the dotted circle is drawn. BD is drawn tangential to dotted circle. AD cuts circle A at C. CE is drawn parallel to DB as the internal tangent [5].
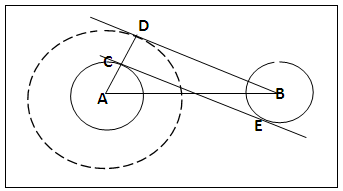 | Figure 9. Internal Tangent by Sum of Radii |
2.2. New Methods of Determining External Homothetic Point and Second Set of Special Radical Points
2.2.1. Determination of External Homothetic Point by Parallel Line Method Using Difference in Radii, Figure 10
- (a). Draw circles A and B as specified; join A and B, figure 10 with the lettering, AC = rA.(b).Draw AP at a convenient angle. Centre C with radius rB, cut CA at D, CD = rB. Join DB, note the directions of AC and CD.(c) Drawn through C a straight line parallel to DB to cut AB produced at F. F is the external homothetic centre.
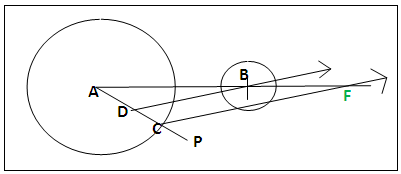 | Figure 10. Use of Difference in Radii to Determine External Homothetic Point (F) |
2.2.2. Determination of Second Set of Special Radical Point by the Use of Mean of the Difference in Radii Figure 11
- The second set of special radical points is the points of intersections of the radical axis and the two internal common tangents.(a). Draw the two circles A and B, join their centres and let O be the midpoint of AB, figure 10 with the lettering. Determine the internal homothetic centre G by any convenient method and the mean of the difference in radii. (rA - rB)/2.(b). Centre O and radius (rA - rB)/2 swing arcs above and below AB. Centre G and same radius, cut the arcs at H and J which are the second set of special radical centres. Equal tangents drawn from each of the two points to the two circles form a straight line tangent which is the same as the internal common tangent.Alternatively, draw the two internal common tangents by any convenient method and the radical axis as in section 2.1.3. The radical axis cuts the internal common tangents at H and J, the second set of special radical points.
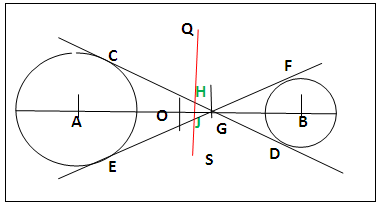 | Figure 11. Determination of Second Set of Special Radical Point (H, J) by the use of Mean of the Difference in Radii |
3. Results and Discussion
3.1. Presentation of Current Methods
- The various methods currently available for the construction of tangents (common and equal) to circles in a two circle system have been published over a long period of time. The methods, though varying in procedures, have in common the indispensable function played by the radii of the two circles. The part played by the radii of the circles occurs in all the constructions either at the preliminary stage of determining the homothetic points (external or internal) or special radical points or in the direct construction of the tangents. To make this contribution of radii of the circles evident, the various existing methods for constructing the homothetic, radical points/axis and the tangents have been re-presented but with brief descriptions with the essential figures. By this manner of re-presentation it is believed that the contributions of the radii of the circles in the constructions will be made vivid, the task of searching the literature in this respect will be reduced and last but not the least, a handy collection of the various methods is provided. The new methods reported here are updates hence they are given full descriptions in their methods.
3.2. External Homothetic Point by Parallel Line Division
- In drawing internal and external homothetic points by secant method, the procedures are virtually the same except for a slight flip of the radius rB going from parallel to anti-parallel to rA. So it was felt that to use the parallel line method to determine the external homothetic point, rB now will be anti-parallel along the same line as rA as shown in section 2.2.1, figure 10 i.e. CD = rB and AD = rA - rB. In ΔADB and ΔACF, figure 10, ∠ABD = ∠AFC (DB<CF by construction); ∠ADB = ∠ACF (DB<CF by construction), ∠A is common so ΔADB and ΔACF are similar. Hence FB/FA = DC/CA = rB/rA. Or AB/AF=AD/AC i.e. (AF-BF)/AF = (AC-CD)/AC i.e. BF/AF = CD/AC = rB/rA. Parallel line method of dividing a straight line can now be used to determine external and internal homothetic points.
3.3. Second Set of Special Radical Point by the Use of Mean of the Difference in Radii
- The determination of the first set of special radical points (section 2.1.3, figure 11) applied (rA + rB)/2 as radius with centres O (midpoint of AB) and G (the internal homothetic centre) to locate them. Following the trends observed in other cases of use of radii, the use of (rA - rB)/2 as radius with same centres should give the second set of the special radical points and so it did. The special radical points are too close to each other and accuracy in their determinations is affected. The alternative method provides a solution to the problem. Or join the centres of a common external and an internal tangents and produce both ways to obtain the radical axis. The radical axis intersects with the internal and external tangents at their mid points and there is only one radical axis per a system of two circles.
|
4. Conclusions
- The aggregation of the current and new methods of constructing homothetic points, radical points/axis and tangents (common or equal) in two circle system shows that the radii of the two circles play vital roles in the constructions. Different combinations of the radii of the two circles as shown in the Table are used to construct the homothetic points, radical axis/points required for the desired tangents. This review with update also show that tangents (common or equal) and radical points/axis are interrelated through the special radical points since the midpoints of the external (or internal) tangents lie on the radical axis. Also a perpendicular to AB through this midpoint is the radical axis of the two circle system. Hence given the tangential distance in a system of two circles or given the distance of AB, with rA and rB the two circle system can be constructed complete with the tangent and the radical axis.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML