Salah H. Abid, Russul K. Abdulrazak
Mathematics Department, Education College, Al-Mustansiriya University, Baghdad, Iraq
Correspondence to: Salah H. Abid, Mathematics Department, Education College, Al-Mustansiriya University, Baghdad, Iraq.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we introduce a new family of continuous distributions based on [0,1] truncated Fréchet distribution. [0,1] truncated Fréchet Generalized Gamma distribution is discussed as special cases. The cumulative distribution function, the rth moment, the mean, the variance, the skewness, the kurtosis, the mode, the median, the characteristic function, the reliability function and the hazard rate function are obtained for the distributions under consideration. It is well known that an item fails when a stress to which it is subjected exceeds the corresponding strength. In this sense, strength can be viewed as resistance to failure. Good design practice is such that the strength is always greater than the expected stress. The safety factor can be defined in terms of strength and stress as strength/ stress. So, the [0,1] TFGG strength-stress model with different parameters will be derived here. The Shannon entropy and Relative entropy will be derived also.
Keywords:
[0,1] TFGG, Stress-strength model, Shannon entropy, Relative entropy
Cite this paper: Salah H. Abid, Russul K. Abdulrazak, [0,1]truncated Fréchet-G Generator of Distributions, Applied Mathematics, Vol. 7 No. 3, 2017, pp. 51-66. doi: 10.5923/j.am.20170703.03.
1. Introduction
Here, we proposed a distribution with the hope it will attract wider applicability in other fields. The generalization which is motivated by the work of Eugene et al. will be our guide. Eugene et al. (2002) [2] defined the beta G distribution from a quite arbitrary cumulative distribution function (cdf), G(x) by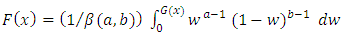 | (1) |
where a > 0 and b > 0 are two additional parameters whose role is to introduce skewness and to vary tail weight and 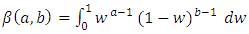 is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) [2] and Jones (2004) [5]. Application of
is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) [2] and Jones (2004) [5]. Application of 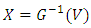 to the random variable V following a beta distribution with parameters a and b, V ∼ B(a, b) say, yields X with cdf (1). Eugene et al. (2002) [2] defined the beta normal (BN) distribution by taking G(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004 [4]). An extensive review of scientific literature on this subject is available in Abid and Hassan (2015) [1]. We can write (1) as,
to the random variable V following a beta distribution with parameters a and b, V ∼ B(a, b) say, yields X with cdf (1). Eugene et al. (2002) [2] defined the beta normal (BN) distribution by taking G(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004 [4]). An extensive review of scientific literature on this subject is available in Abid and Hassan (2015) [1]. We can write (1) as,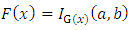 | (2) |
Where, 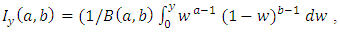 denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by,
denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by, 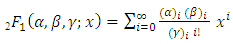 Where
Where 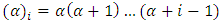 denotes the ascending factorial. We obtain,
denotes the ascending factorial. We obtain,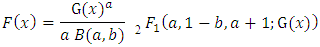 The properties of the cdf, F(x) for any beta G distribution defined from a parent
The properties of the cdf, F(x) for any beta G distribution defined from a parent 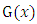 in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [3]. The probability density function (pdf) corresponding to (1) can be written in the form,
in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [3]. The probability density function (pdf) corresponding to (1) can be written in the form,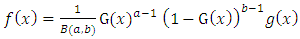 | (3) |
where 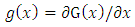 is the pdf of the parent distribution.Now, since the pdf and cdf of [0,1] truncated Fréchet distribution are respectively,
is the pdf of the parent distribution.Now, since the pdf and cdf of [0,1] truncated Fréchet distribution are respectively, 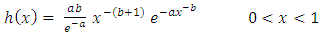 | (4) |
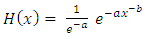 | (5) |
Graphs for some arbitrary parameters values of pdf and cdf are shown in figure (1) and figure (2) respectively,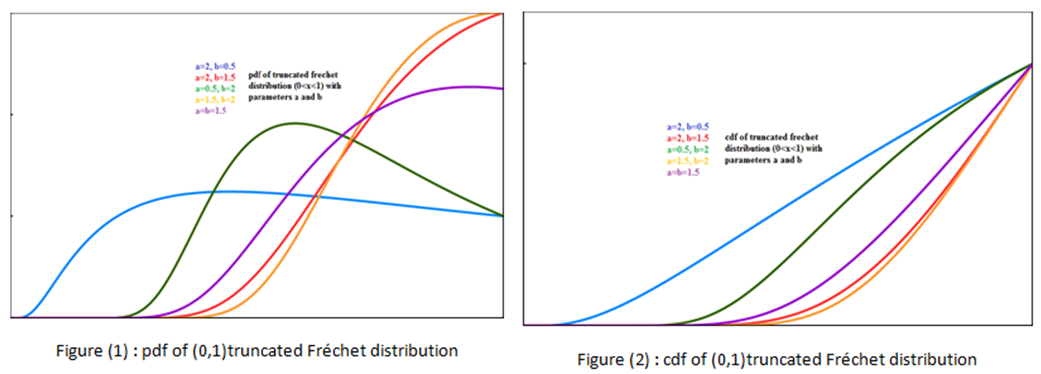 | Figure 1 and 2 |
Now, Given two absolutely continuous cdfs, H and G, so that h and g are their corresponding pdfs. We suggest a new distribution F by composing H with G, so that 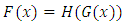 is a CDF,
is a CDF,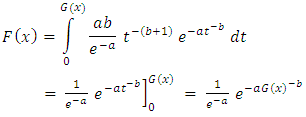 | (6) |
With pdf, 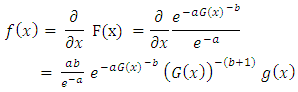 | (7) |
With 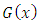 being a baseline distribution, we define in (6) and (7) above, a generalized class of distributions. We will name it the [0,1] truncated Fréchet -G distribution. In the following section, we will assume that G is Generalized Gamma distribution.
being a baseline distribution, we define in (6) and (7) above, a generalized class of distributions. We will name it the [0,1] truncated Fréchet -G distribution. In the following section, we will assume that G is Generalized Gamma distribution.
2. [0,1] truncated Fréchet-generalized Gamma Distribution
Assume that 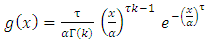 and
and 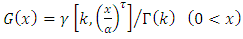 are pdf and cdf of Generalized Gamma random variable [6, 8] respectively, then, by applying (6) and (7) above, we get the cdf pdf of [0,1] TFGG random variable as follows,
are pdf and cdf of Generalized Gamma random variable [6, 8] respectively, then, by applying (6) and (7) above, we get the cdf pdf of [0,1] TFGG random variable as follows, 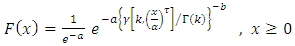 | (8) |
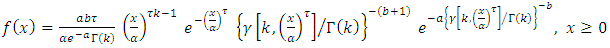 | (9) |
So, the reliability and hazard rate function are respectively 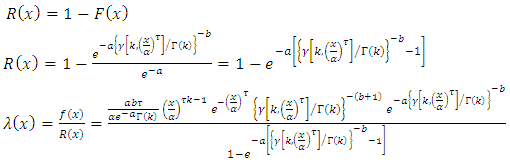 The rth raw moment can be derived as follows,
The rth raw moment can be derived as follows, 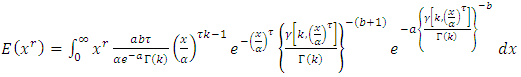 Since,
Since, 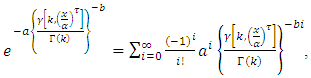 then,
then, 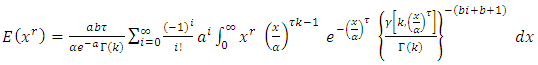 Since,
Since, 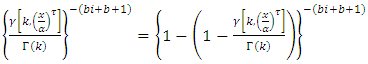 By using,
By using, 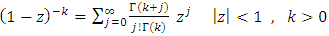 and
and 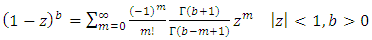 | (10) |
We get,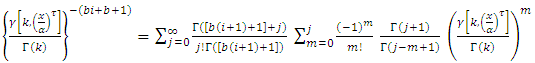 and then,
and then, 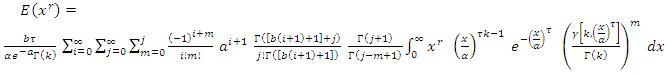 let
let 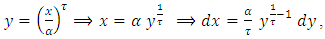 then,
then,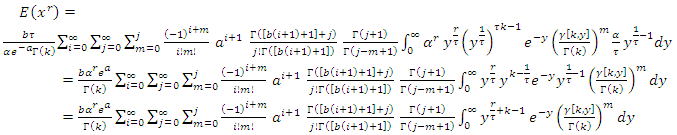 By using [6],
By using [6], 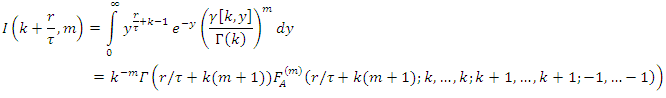 | (11) |
Where, 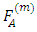 is the Lauricella function of type A, then,
is the Lauricella function of type A, then,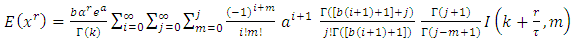 | (12) |
And then, the characteristic function is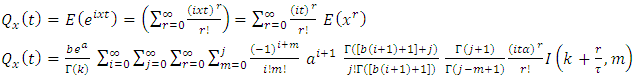 So, the mean
So, the mean 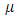 and variance
and variance 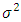 of the of [0,1] TFGG random variable are,
of the of [0,1] TFGG random variable are,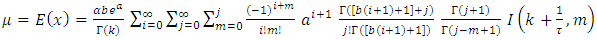 | (13) |
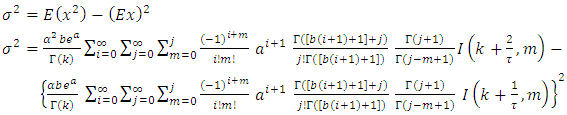 | (14) |
Since, 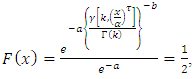 then By solving the nonlinear equation
then By solving the nonlinear equation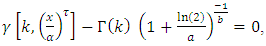 we obtain the median of X. The skewness of [0,1] TFGG random variable will be,
we obtain the median of X. The skewness of [0,1] TFGG random variable will be, 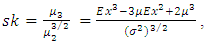 so
so | (15) |
Also, the kurtosis is, | (16) |
The quantile function 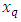 of [0,1] TFGG random variable can be obtained by solving the following nonlinear equation as,
of [0,1] TFGG random variable can be obtained by solving the following nonlinear equation as,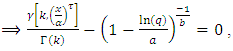 since
since 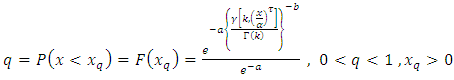 So by using inverse transform method we can generate [0,1] TFGG random variable as follows,
So by using inverse transform method we can generate [0,1] TFGG random variable as follows, 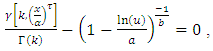 Where U is uniformly distributed random number in the unit interval [0,1].
Where U is uniformly distributed random number in the unit interval [0,1].
2.1. Shannon and Relative Entropies
An entropy of a random variable X is a measure of variation of the uncertainty. The Shannon entropy of 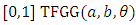 random variable X can be found as follows,
random variable X can be found as follows,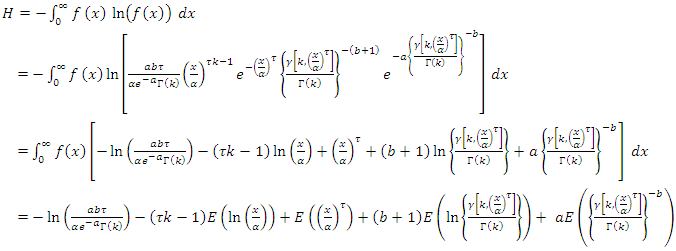 Let,
Let, 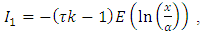
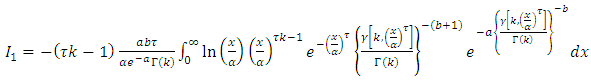 Since,
Since, 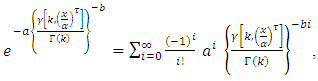 then
then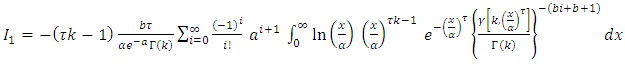 By using equation (10) we get,
By using equation (10) we get,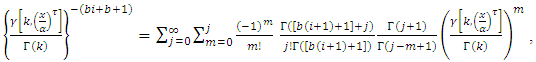 and then,
and then, 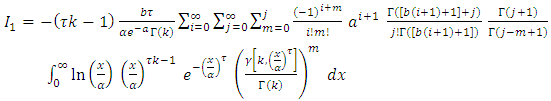 by using expansion series incomplete Gamma function
by using expansion series incomplete Gamma function 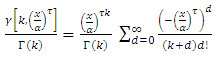 | (17) |
We get,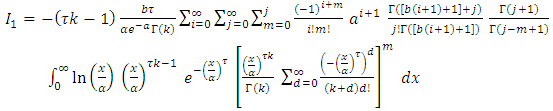 let
let 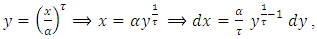 then,
then,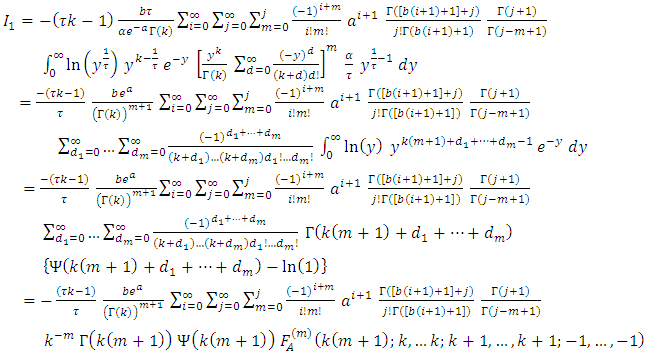 Now, since the Lauricella function of type A,
Now, since the Lauricella function of type A, 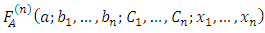 can be defined as
can be defined as 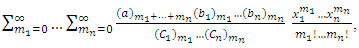 where
where 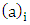 is the ascending factorial defined by
is the ascending factorial defined by 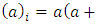
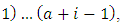 (with the convention that
(with the convention that 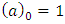 ).
).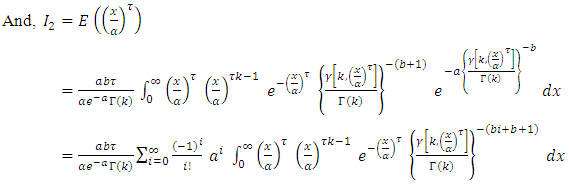 by using equation (10) we get,
by using equation (10) we get,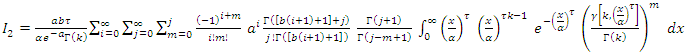 let
let 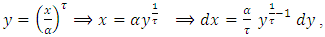 then,
then,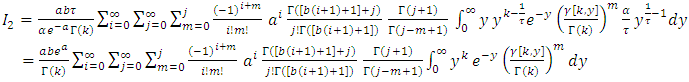 By using equation (11) we get,
By using equation (11) we get, 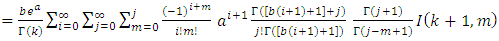 and,
and,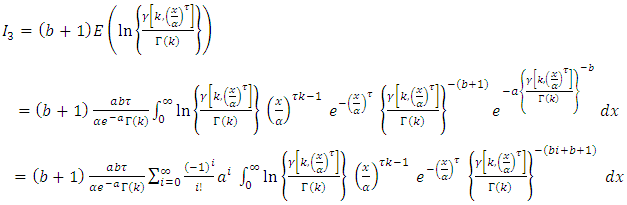 By using equation (10) we get,
By using equation (10) we get, 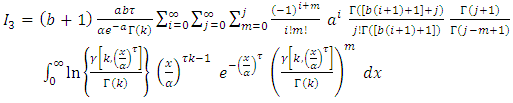 By using expansion series of incomplete Gamma function, we get
By using expansion series of incomplete Gamma function, we get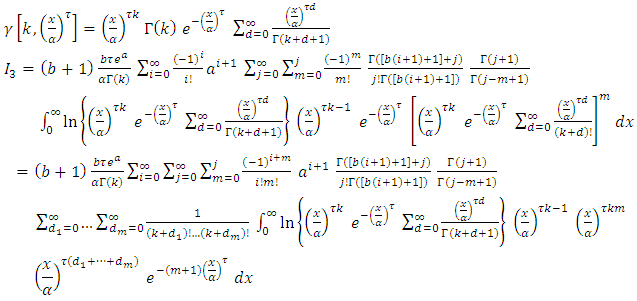 Since,
Since, 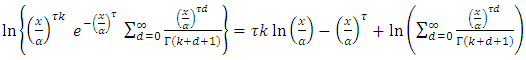
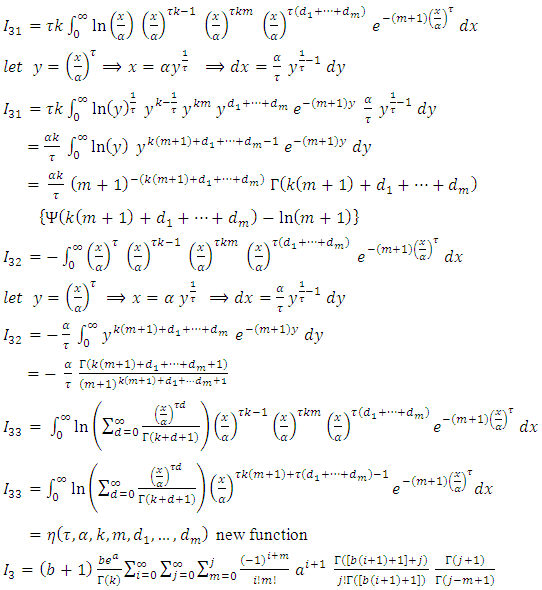
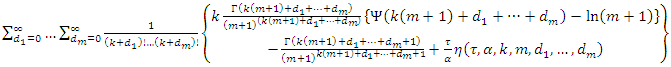
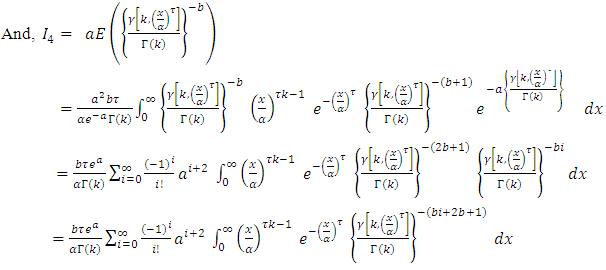 By using (10) we get,
By using (10) we get,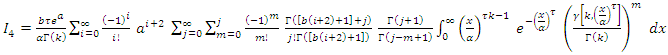 let
let 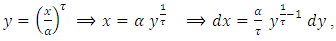 then,
then, 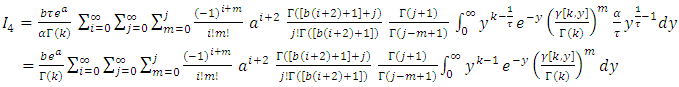 By using (11) we get,
By using (11) we get,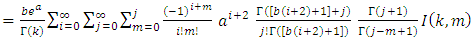 then
then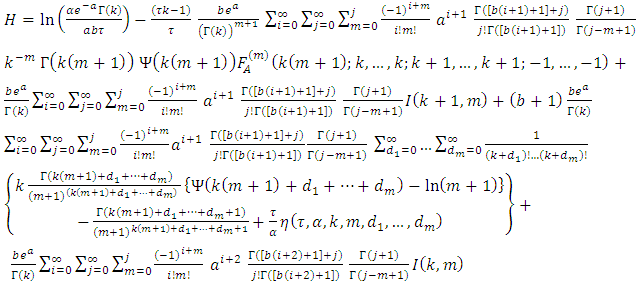 | (18) |
The relative entropy (or the Kullback–Leibler divergence) is a measure of the difference between two probability distributions 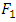 and
and 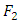 . It is not symmetric in
. It is not symmetric in 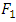 and
and 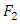 . In applications,
. In applications, 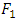 typically represents the "true" distribution of data, observations, or a precisely calculated theoretical distribution, while
typically represents the "true" distribution of data, observations, or a precisely calculated theoretical distribution, while 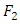 typically represents a theory, model, description, or approximation of
typically represents a theory, model, description, or approximation of 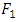 . Specifically, the Kullback–Leibler divergence of
. Specifically, the Kullback–Leibler divergence of 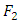 from
from 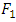 , denoted
, denoted 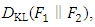 is a measure of the information gained when one revises ones beliefs from the prior probability distribution
is a measure of the information gained when one revises ones beliefs from the prior probability distribution 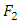 to the posterior probability distribution
to the posterior probability distribution 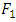 . More exactly, it is the amount of information that is lost when
. More exactly, it is the amount of information that is lost when 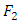 is used to approximate
is used to approximate 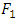 , defined operationally as the expected extra number of bits required to code samples from
, defined operationally as the expected extra number of bits required to code samples from 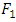 using a code optimized for
using a code optimized for 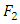 rather than the code optimized for
rather than the code optimized for 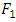 . The relative entropy
. The relative entropy 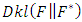 for a random variable
for a random variable 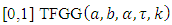 can be found as follows,
can be found as follows, 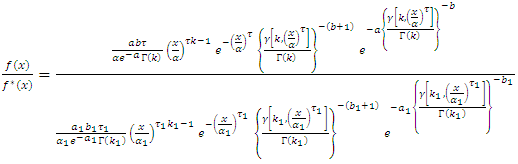
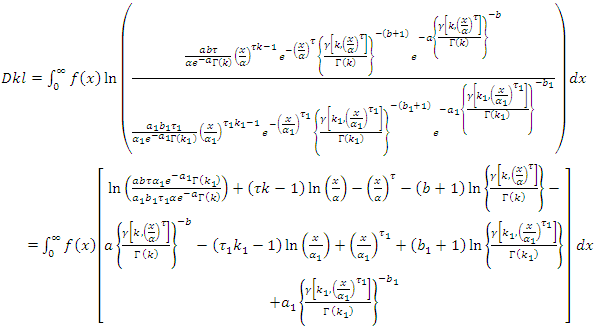 Let,
Let, 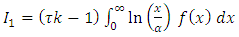
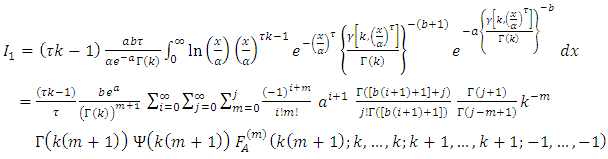 And,
And, 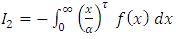
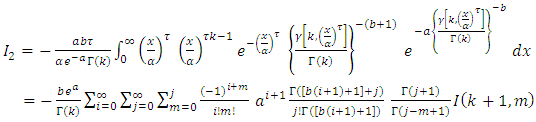 And,
And, 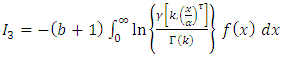
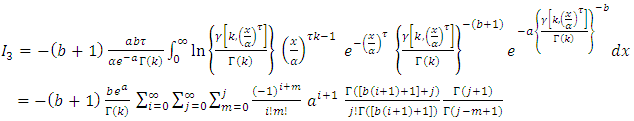
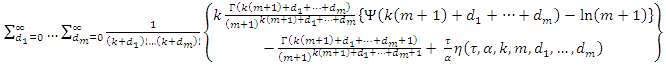 And,
And, 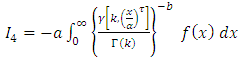
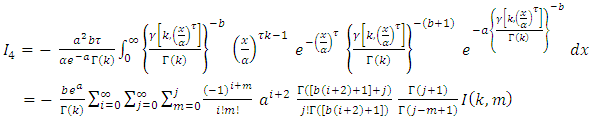 And,
And, 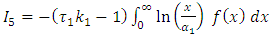
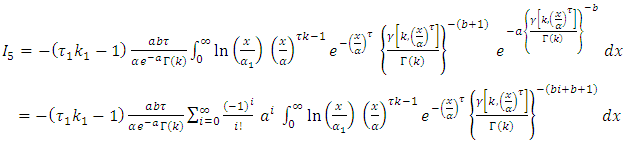 By using equation (10) we get,
By using equation (10) we get,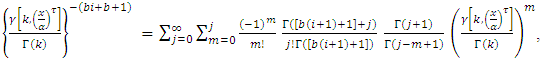 then,
then,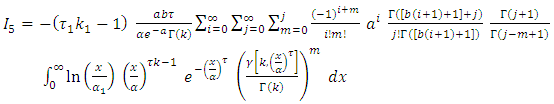 By using equation (17) we get,
By using equation (17) we get,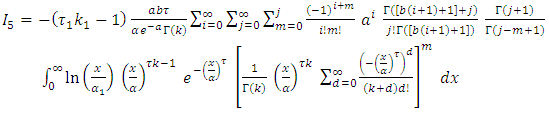 By applying of equation in section 0.314 of Gradshteyn and Ryzhik (2000) [3] for power series raised to power, we obtain for any m positive integer
By applying of equation in section 0.314 of Gradshteyn and Ryzhik (2000) [3] for power series raised to power, we obtain for any m positive integer 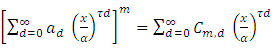 Where the coefficients
Where the coefficients 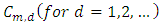 satisfy the recurrence relation
satisfy the recurrence relation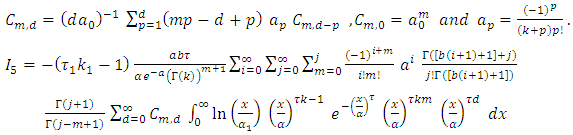 let
let 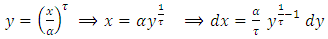
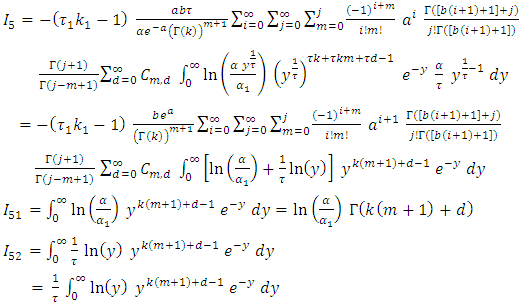 Since
Since 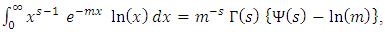 then
then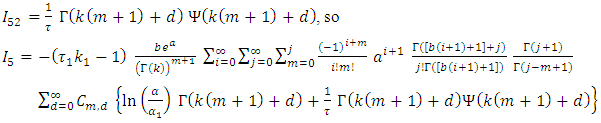 And,
And, 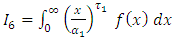
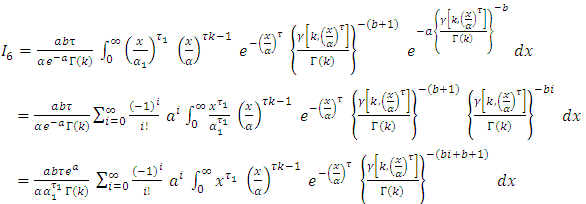 By using equation (10) we get,
By using equation (10) we get,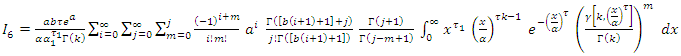 let
let 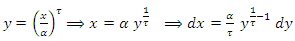 , then,
, then,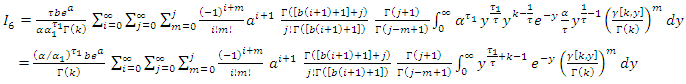 By using (11) we get,
By using (11) we get,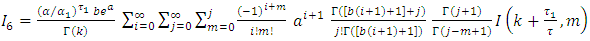 Since,
Since, 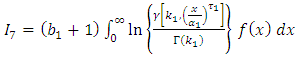
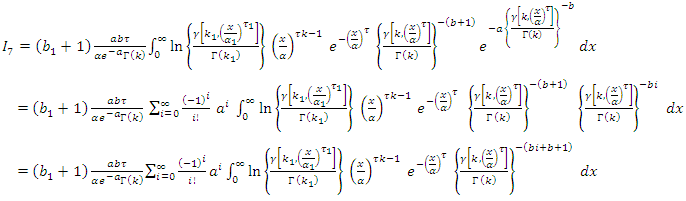 By using equation (10) we get,
By using equation (10) we get,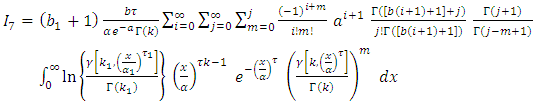 By using expansion series of incomplete Gamma function
By using expansion series of incomplete Gamma function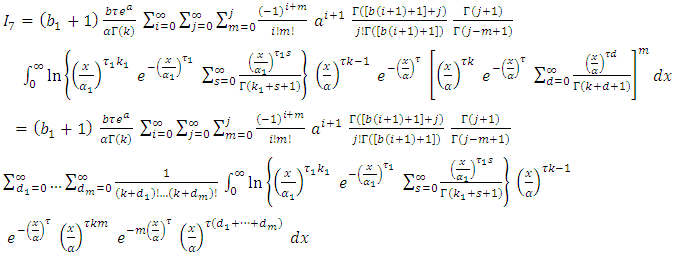 Since,
Since, 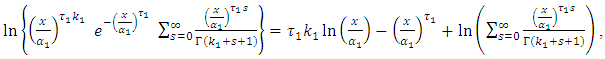 then,
then,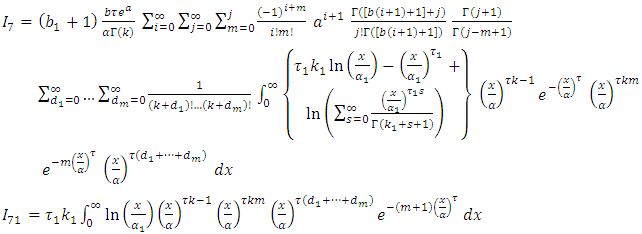 let
let 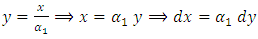
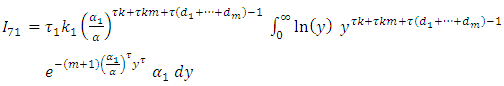 let
let 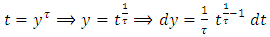
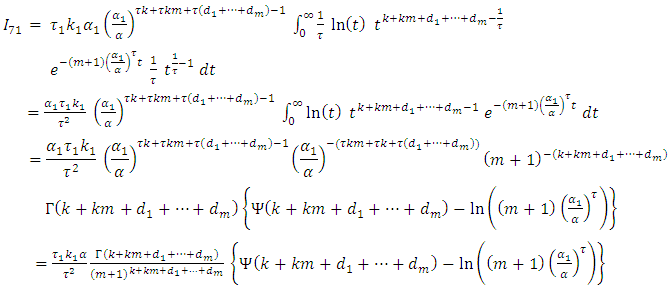 And,
And, 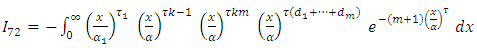 let
let 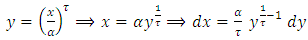
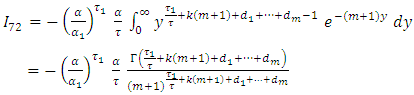
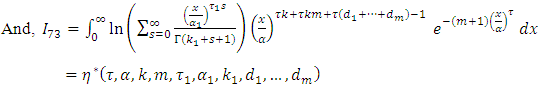
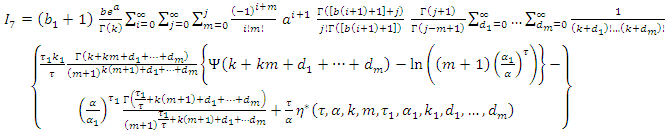 Since,
Since, 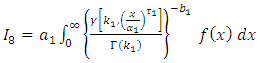
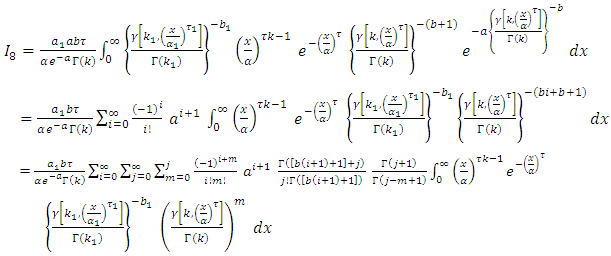 Since,
Since, 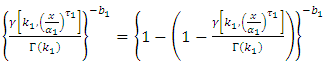 By using equation (10) we get,
By using equation (10) we get, 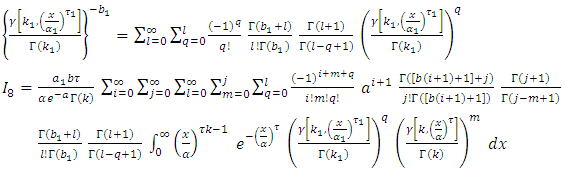 By using eq. expansion of incomplete gamma (17) we get,
By using eq. expansion of incomplete gamma (17) we get,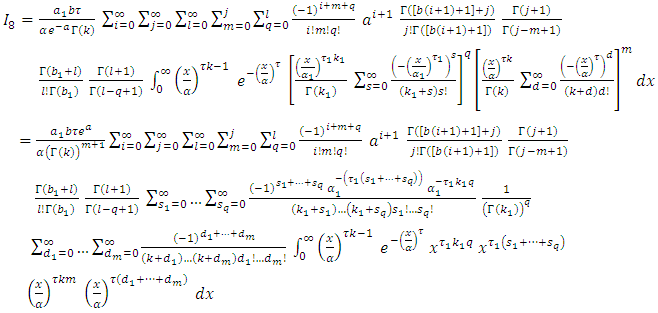 let
let 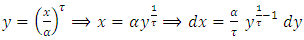 Since,
Since, 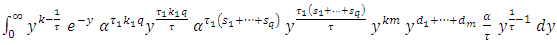
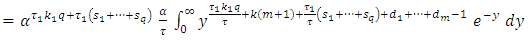
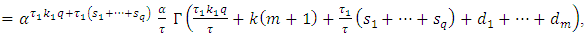 then,
then,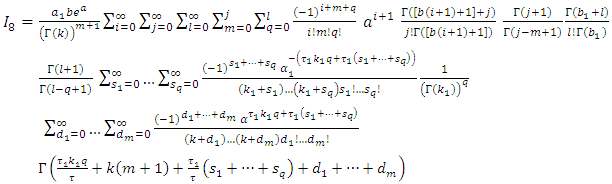 So
So 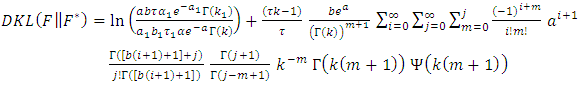
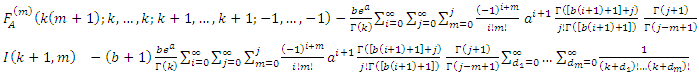
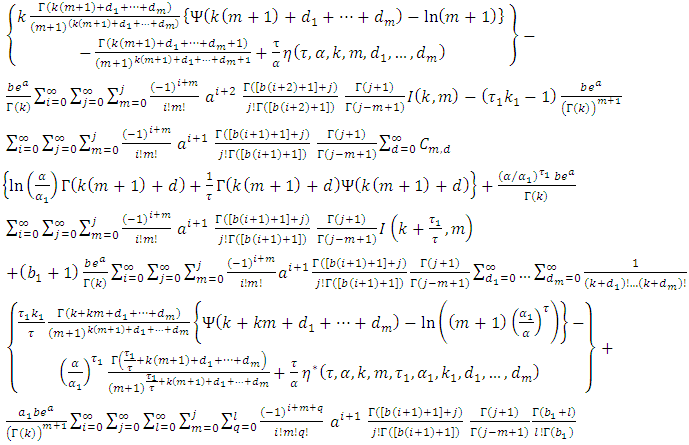
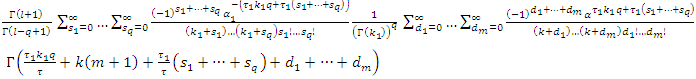 | (19) |
2.2. Stress-Strength Reliability
Let y and x be the stress and strength random variable, independent of each other, follow respectively [0,1] 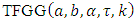 and [0,1]
and [0,1] 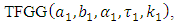 then,
then, 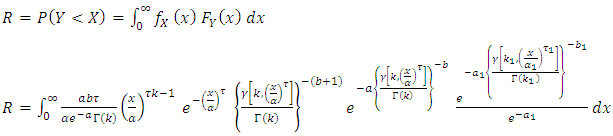 Since,
Since, 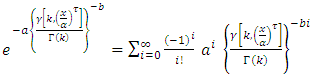 and
and 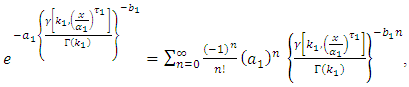 then,
then,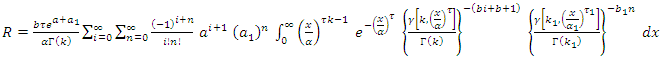 By using equation (10) we get,
By using equation (10) we get, 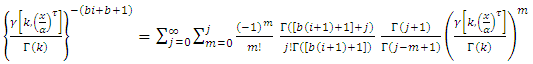
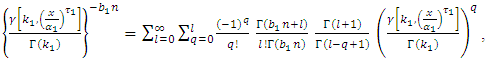 then,
then,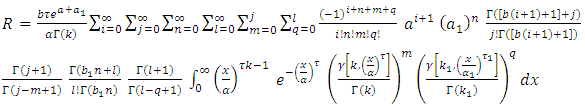 By using expansion of incomplete gamma function (17) we get,
By using expansion of incomplete gamma function (17) we get,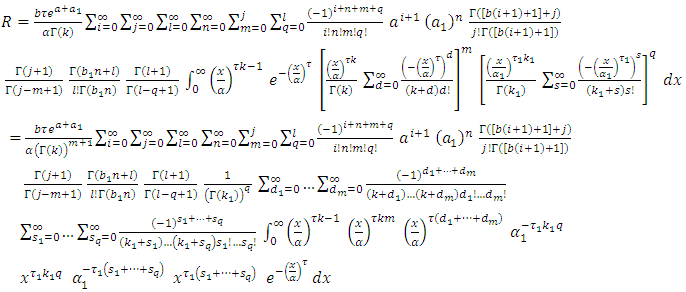 let
let 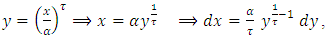 then,
then, 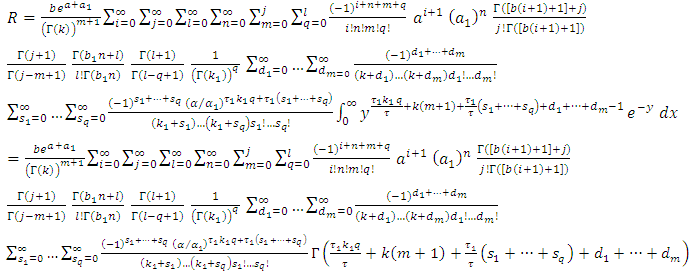 | (20) |
3. Summary and Conclusions
In statistical analysis a lot of distributions are used to represent set(s) of data. Recently, new distributions are derived to extend some of well-known families of distributions, such that the new distributions are more flexible than the others to model real data. The composing of some distributions with each other's in some way has been in the foreword of data modeling. In this paper, we presented a new family of continuous distributions based on [0,1] truncated Fréchet distribution. [0,1] truncated Fréchet Generalized Gamma ([0,1]TFGG) distribution is discussed as special case. Properties of [0,1] TFGG is derived. We provide form for characteristic function, rth raw moment, mean, variance, skewness, kurtosis, mode, median, reliability function, hazard rate function, Shannon entropy function and Relative entropy function. This paper deals also with the determination of stress-strength R=p[y<x] when x (strength) and y (stress) are two independent [0,1] TFGG distribution with different parameters.
References
| [1] | Abid, S., Hassan, H. (2015) "The Beta Marshall-Olkin Extended Uniform Distribution"; Journal of Safety Engineering 2015, 4(1): 1-7. |
| [2] | Eugene, N., Lee, C., Famoye, F. (2002) "Beta-normal distribution and its applications" Commun.Statist. - Theory and Methods 31:497-512. |
| [3] | Gradshteyn, I.S., Ryzhik, I.M. (2000) "Table of integrals, series, and products" Academic Press, San Diego. |
| [4] | Gupta, A.K., Nadarajah, S. (2004) "On the moments of the beta normal distribution" Commun. Statist. - Theory and Methods 33:1-13. |
| [5] | Jones, M.C. (2004)"Families of distributions arising from distributions of order statistics" Test 13:1-43. |
| [6] | Marcelino A. & Edwin M. & Gauss M. and Patricia F. (2011) "The Kumaraswamy-Generalized Gamma distribution with Application in survival Analysis"; Statistical Methodology, Volume 8, Issue 5, September 2011, Pages 411-433. |
| [7] | Nadarajah, S. (2008), "Explicit expressions for moments of 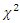 order statistics", Vol.3 (2008), No.3, pp.433-444. order statistics", Vol.3 (2008), No.3, pp.433-444. |
| [8] | Temme, N. (1994) "Computational aspects of incomplete Gamma functions with large complex parameters", international series of Numerical Mathematics, Vol.119, p.551-562. |



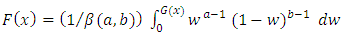
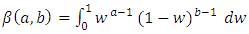 is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) [2] and Jones (2004) [5]. Application of
is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) [2] and Jones (2004) [5]. Application of 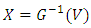 to the random variable V following a beta distribution with parameters a and b, V ∼ B(a, b) say, yields X with cdf (1). Eugene et al. (2002) [2] defined the beta normal (BN) distribution by taking G(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004 [4]). An extensive review of scientific literature on this subject is available in Abid and Hassan (2015) [1]. We can write (1) as,
to the random variable V following a beta distribution with parameters a and b, V ∼ B(a, b) say, yields X with cdf (1). Eugene et al. (2002) [2] defined the beta normal (BN) distribution by taking G(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004 [4]). An extensive review of scientific literature on this subject is available in Abid and Hassan (2015) [1]. We can write (1) as,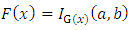
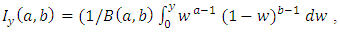 denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by,
denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by, 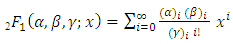 Where
Where 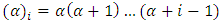 denotes the ascending factorial. We obtain,
denotes the ascending factorial. We obtain,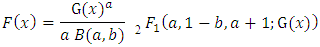 The properties of the cdf, F(x) for any beta G distribution defined from a parent
The properties of the cdf, F(x) for any beta G distribution defined from a parent 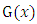 in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [3]. The probability density function (pdf) corresponding to (1) can be written in the form,
in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [3]. The probability density function (pdf) corresponding to (1) can be written in the form,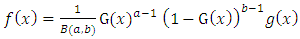
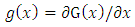 is the pdf of the parent distribution.Now, since the pdf and cdf of [0,1] truncated Fréchet distribution are respectively,
is the pdf of the parent distribution.Now, since the pdf and cdf of [0,1] truncated Fréchet distribution are respectively, 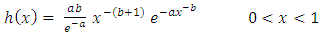
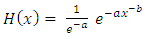

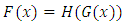 is a CDF,
is a CDF,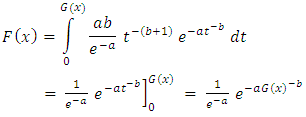
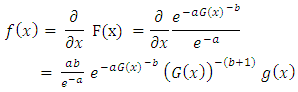
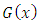 being a baseline distribution, we define in (6) and (7) above, a generalized class of distributions. We will name it the [0,1] truncated Fréchet -G distribution. In the following section, we will assume that G is Generalized Gamma distribution.
being a baseline distribution, we define in (6) and (7) above, a generalized class of distributions. We will name it the [0,1] truncated Fréchet -G distribution. In the following section, we will assume that G is Generalized Gamma distribution.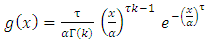 and
and 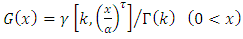 are pdf and cdf of Generalized Gamma random variable [6, 8] respectively, then, by applying (6) and (7) above, we get the cdf pdf of [0,1] TFGG random variable as follows,
are pdf and cdf of Generalized Gamma random variable [6, 8] respectively, then, by applying (6) and (7) above, we get the cdf pdf of [0,1] TFGG random variable as follows, 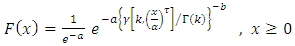
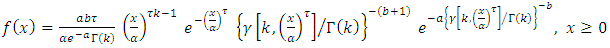
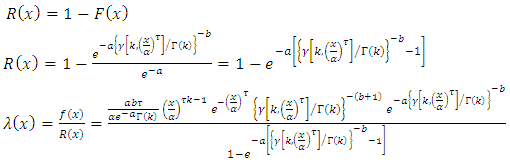 The rth raw moment can be derived as follows,
The rth raw moment can be derived as follows, 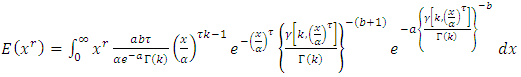 Since,
Since, 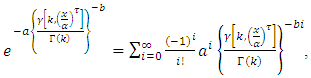 then,
then, 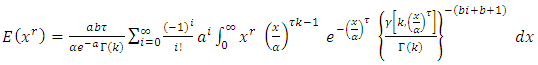 Since,
Since, 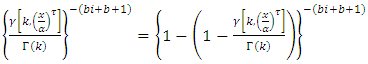 By using,
By using, 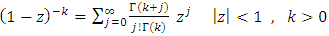 and
and 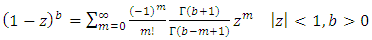
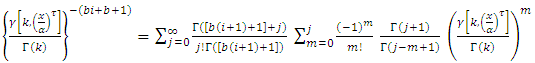 and then,
and then, 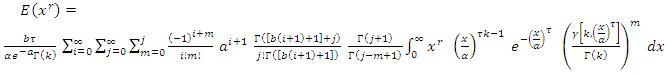 let
let 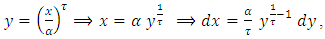 then,
then,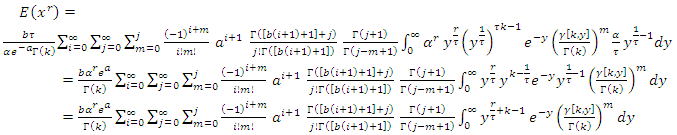 By using [6],
By using [6], 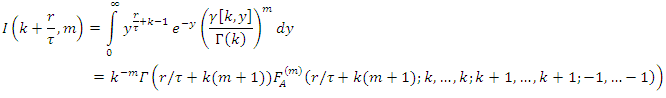
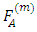 is the Lauricella function of type A, then,
is the Lauricella function of type A, then,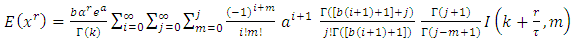
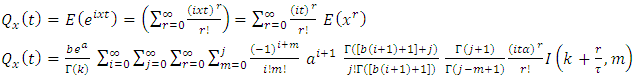 So, the mean
So, the mean 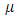 and variance
and variance 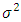 of the of [0,1] TFGG random variable are,
of the of [0,1] TFGG random variable are,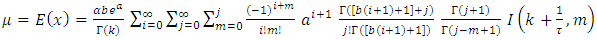
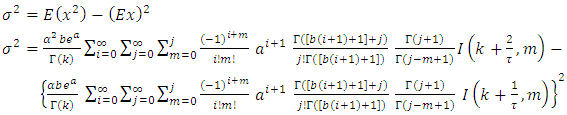
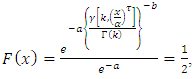 then By solving the nonlinear equation
then By solving the nonlinear equation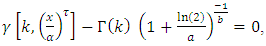 we obtain the median of X. The skewness of [0,1] TFGG random variable will be,
we obtain the median of X. The skewness of [0,1] TFGG random variable will be, 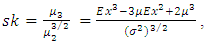 so
so

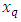 of [0,1] TFGG random variable can be obtained by solving the following nonlinear equation as,
of [0,1] TFGG random variable can be obtained by solving the following nonlinear equation as,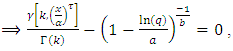 since
since 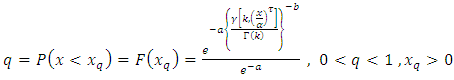 So by using inverse transform method we can generate [0,1] TFGG random variable as follows,
So by using inverse transform method we can generate [0,1] TFGG random variable as follows, 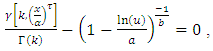 Where U is uniformly distributed random number in the unit interval [0,1].
Where U is uniformly distributed random number in the unit interval [0,1].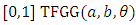 random variable X can be found as follows,
random variable X can be found as follows,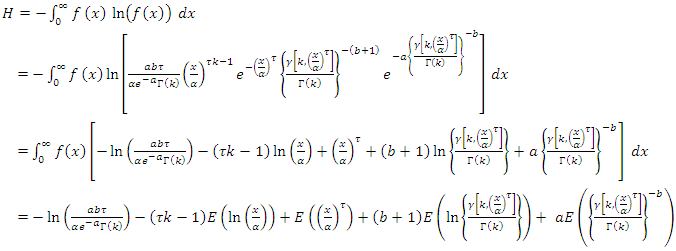 Let,
Let, 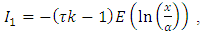
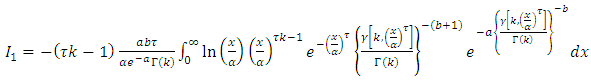 Since,
Since, 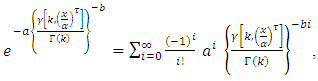 then
then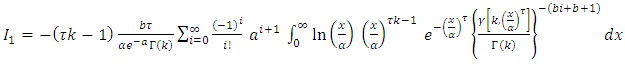 By using equation (10) we get,
By using equation (10) we get,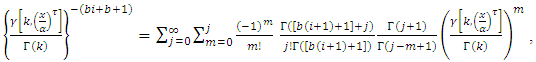 and then,
and then, 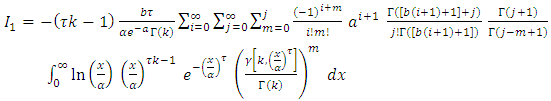 by using expansion series incomplete Gamma function
by using expansion series incomplete Gamma function 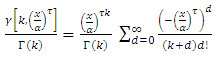
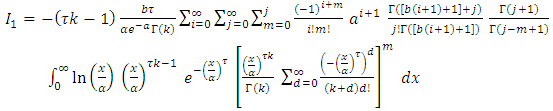 let
let 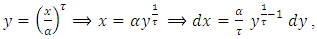 then,
then,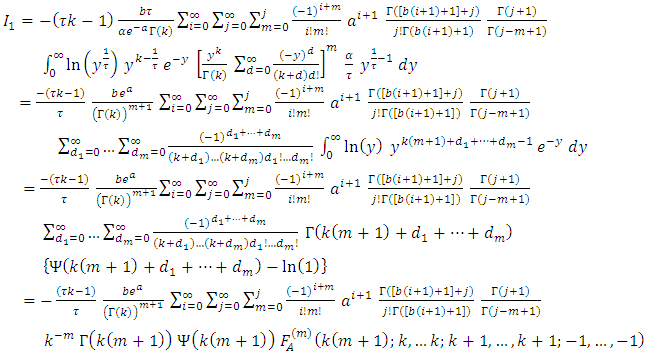 Now, since the Lauricella function of type A,
Now, since the Lauricella function of type A, 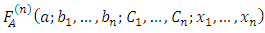 can be defined as
can be defined as 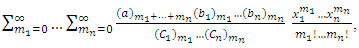 where
where 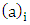 is the ascending factorial defined by
is the ascending factorial defined by 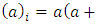
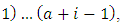 (with the convention that
(with the convention that 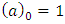 ).
).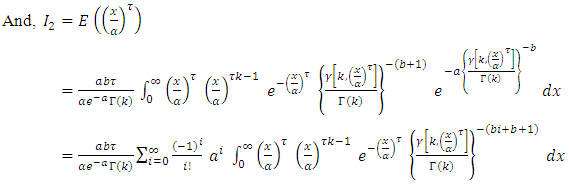 by using equation (10) we get,
by using equation (10) we get,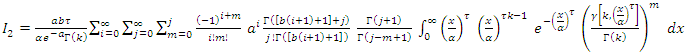 let
let 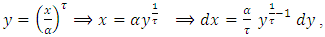 then,
then,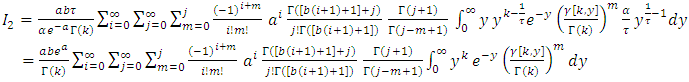 By using equation (11) we get,
By using equation (11) we get, 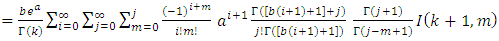 and,
and,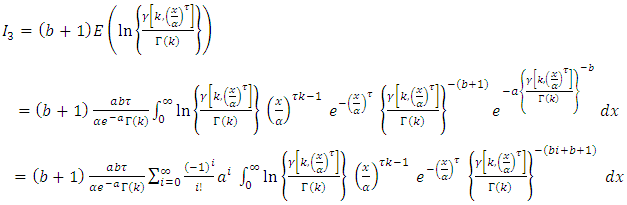 By using equation (10) we get,
By using equation (10) we get, 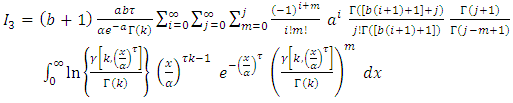 By using expansion series of incomplete Gamma function, we get
By using expansion series of incomplete Gamma function, we get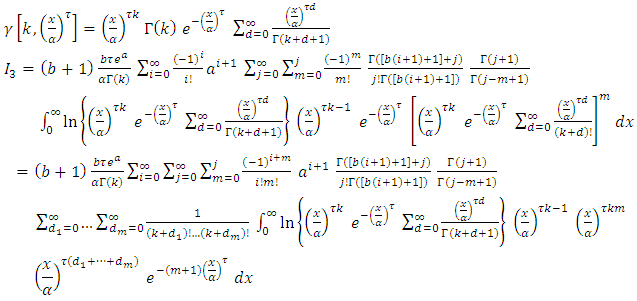 Since,
Since, 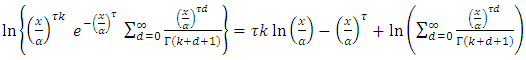
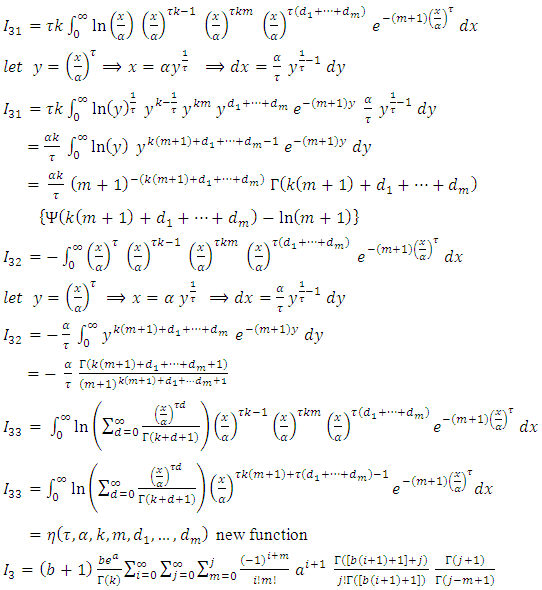
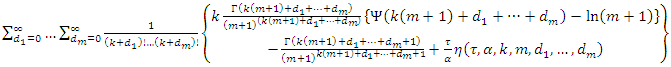
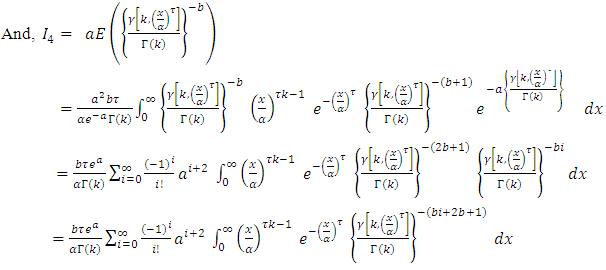 By using (10) we get,
By using (10) we get,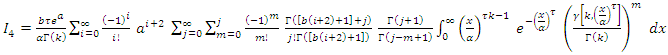 let
let 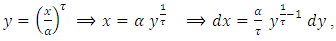 then,
then, 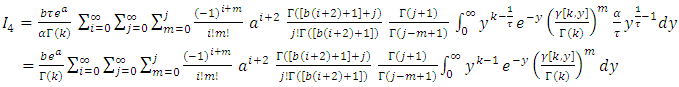 By using (11) we get,
By using (11) we get,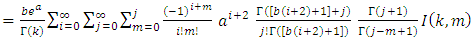 then
then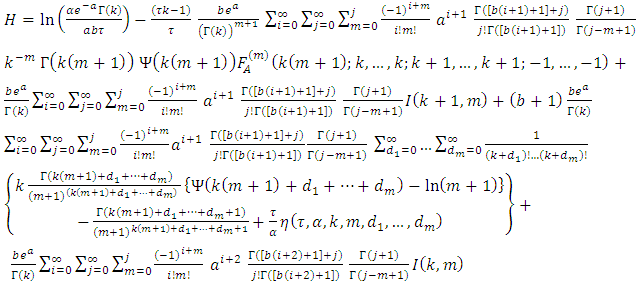
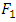 and
and 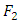 . It is not symmetric in
. It is not symmetric in 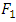 and
and 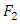 . In applications,
. In applications, 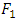 typically represents the "true" distribution of data, observations, or a precisely calculated theoretical distribution, while
typically represents the "true" distribution of data, observations, or a precisely calculated theoretical distribution, while 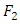 typically represents a theory, model, description, or approximation of
typically represents a theory, model, description, or approximation of 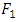 . Specifically, the Kullback–Leibler divergence of
. Specifically, the Kullback–Leibler divergence of 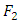 from
from 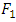 , denoted
, denoted 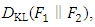 is a measure of the information gained when one revises ones beliefs from the prior probability distribution
is a measure of the information gained when one revises ones beliefs from the prior probability distribution 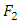 to the posterior probability distribution
to the posterior probability distribution 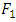 . More exactly, it is the amount of information that is lost when
. More exactly, it is the amount of information that is lost when 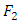 is used to approximate
is used to approximate 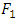 , defined operationally as the expected extra number of bits required to code samples from
, defined operationally as the expected extra number of bits required to code samples from 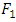 using a code optimized for
using a code optimized for 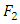 rather than the code optimized for
rather than the code optimized for 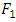 . The relative entropy
. The relative entropy 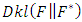 for a random variable
for a random variable 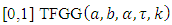 can be found as follows,
can be found as follows, 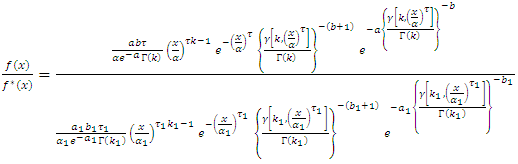
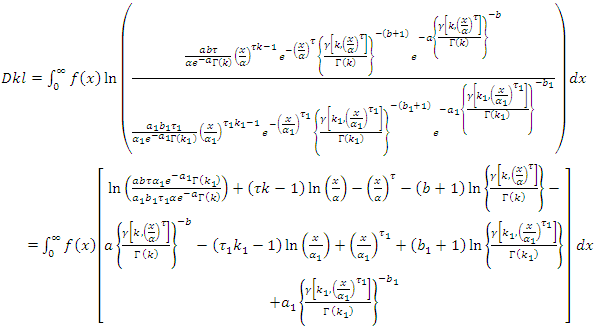 Let,
Let, 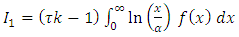
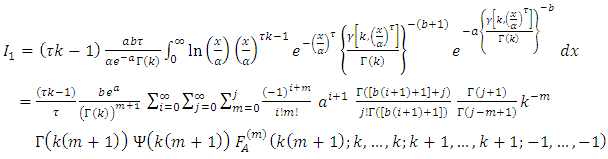 And,
And, 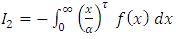
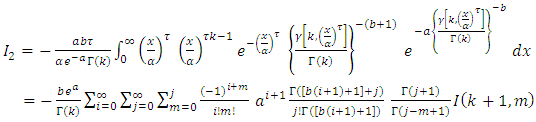 And,
And, 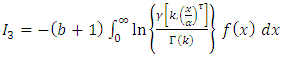
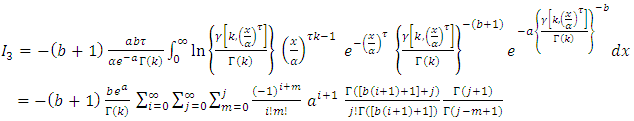
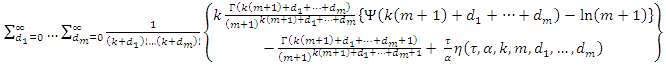 And,
And, 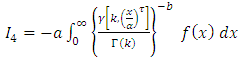
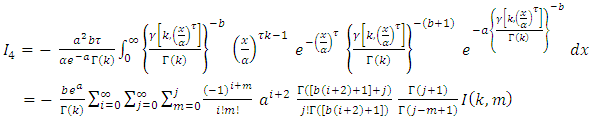 And,
And, 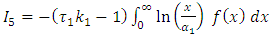
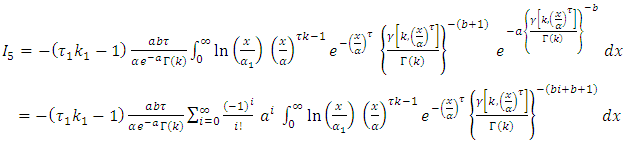 By using equation (10) we get,
By using equation (10) we get,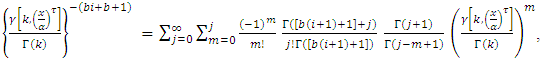 then,
then,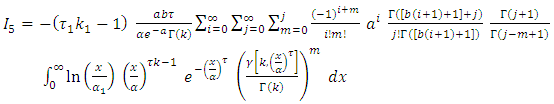 By using equation (17) we get,
By using equation (17) we get,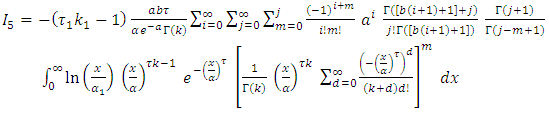 By applying of equation in section 0.314 of Gradshteyn and Ryzhik (2000) [3] for power series raised to power, we obtain for any m positive integer
By applying of equation in section 0.314 of Gradshteyn and Ryzhik (2000) [3] for power series raised to power, we obtain for any m positive integer 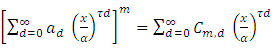 Where the coefficients
Where the coefficients 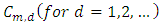 satisfy the recurrence relation
satisfy the recurrence relation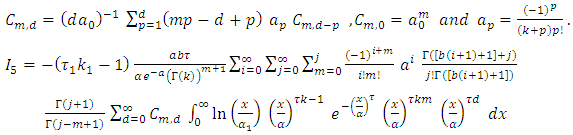 let
let 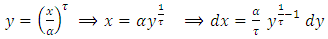
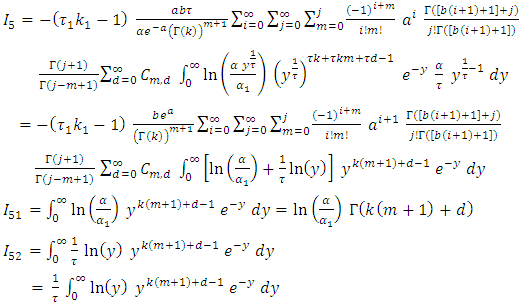 Since
Since 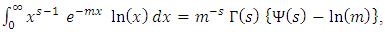 then
then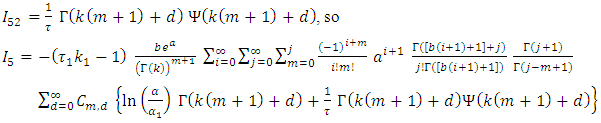 And,
And, 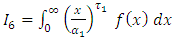
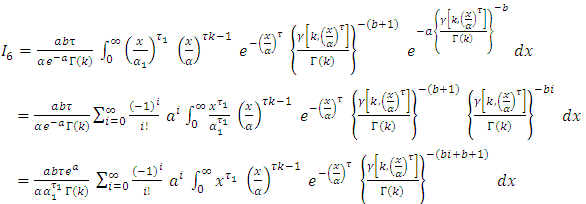 By using equation (10) we get,
By using equation (10) we get,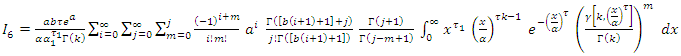 let
let 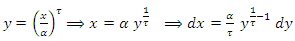 , then,
, then,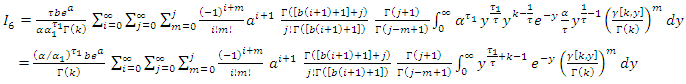 By using (11) we get,
By using (11) we get,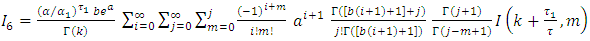 Since,
Since, 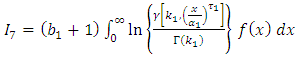
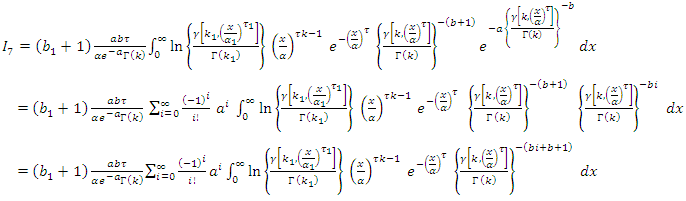 By using equation (10) we get,
By using equation (10) we get,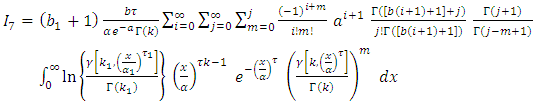 By using expansion series of incomplete Gamma function
By using expansion series of incomplete Gamma function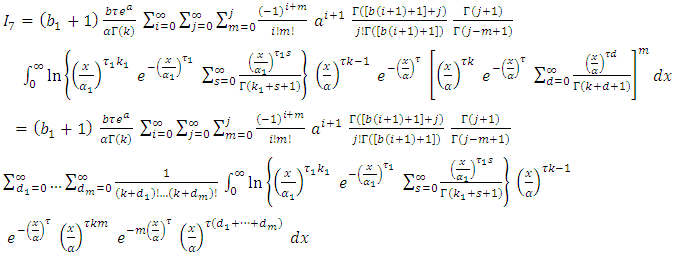 Since,
Since, 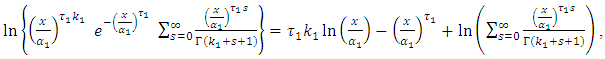 then,
then,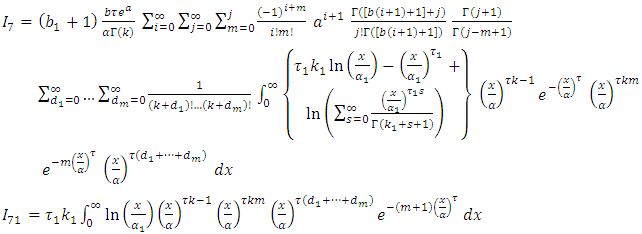 let
let 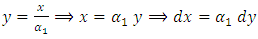
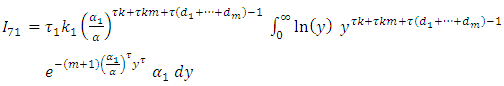 let
let 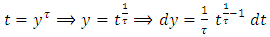
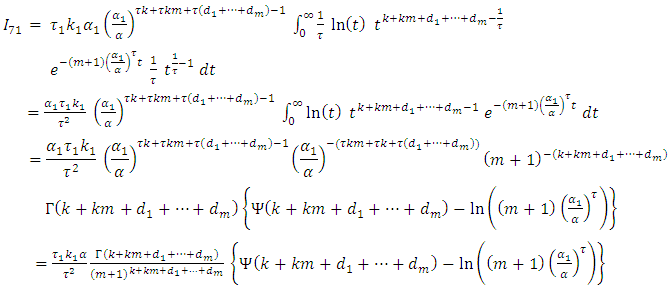 And,
And, 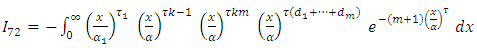 let
let 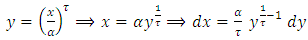
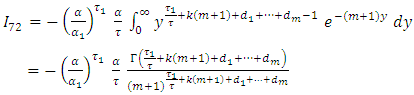
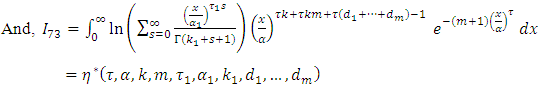
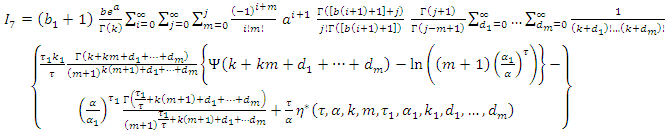 Since,
Since, 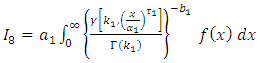
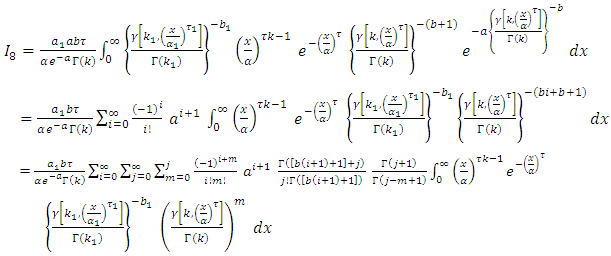 Since,
Since, 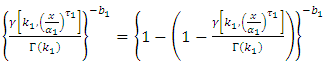 By using equation (10) we get,
By using equation (10) we get, 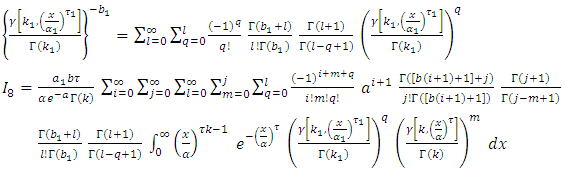 By using eq. expansion of incomplete gamma (17) we get,
By using eq. expansion of incomplete gamma (17) we get,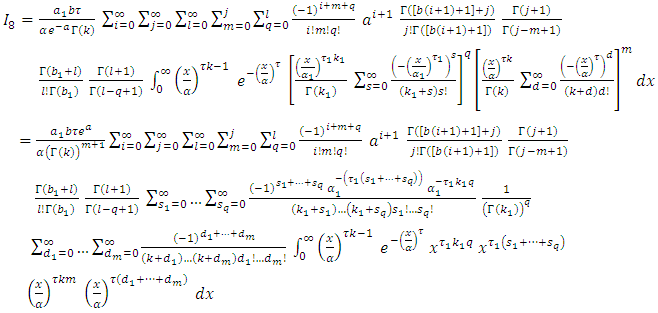 let
let 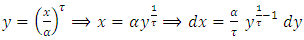 Since,
Since, 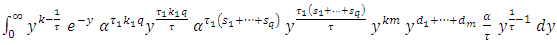
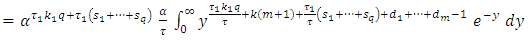
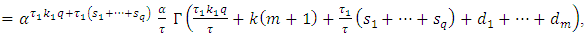 then,
then,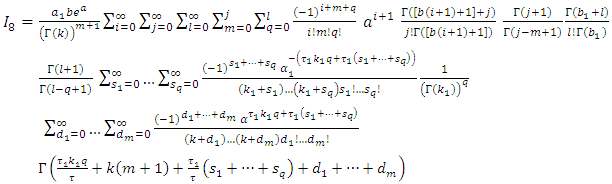 So
So 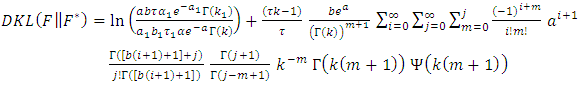
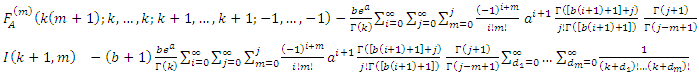
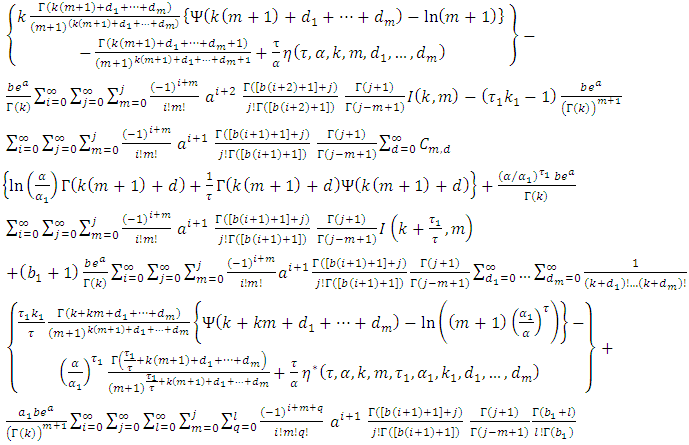
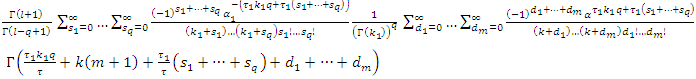
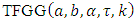 and [0,1]
and [0,1] 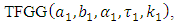 then,
then, 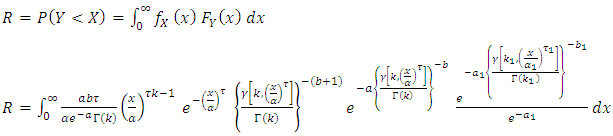 Since,
Since, 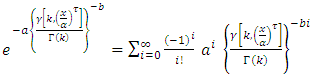 and
and 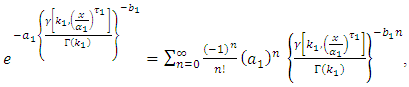 then,
then,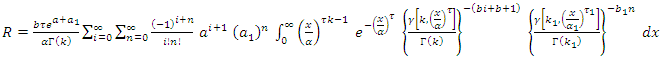 By using equation (10) we get,
By using equation (10) we get, 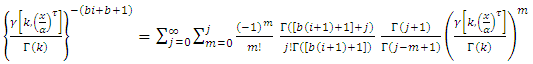
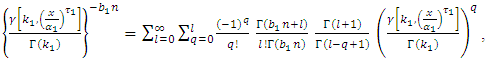 then,
then,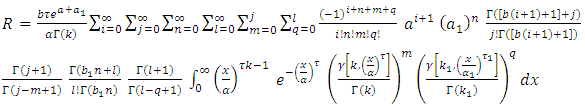 By using expansion of incomplete gamma function (17) we get,
By using expansion of incomplete gamma function (17) we get,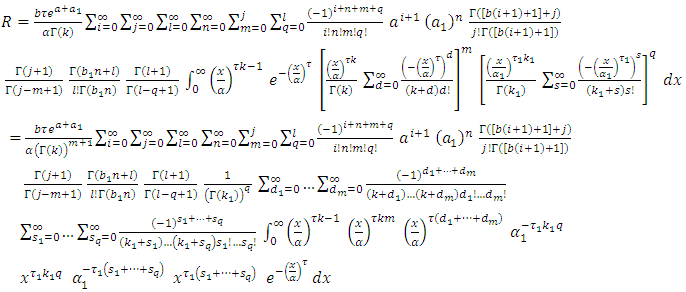 let
let 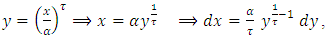 then,
then, 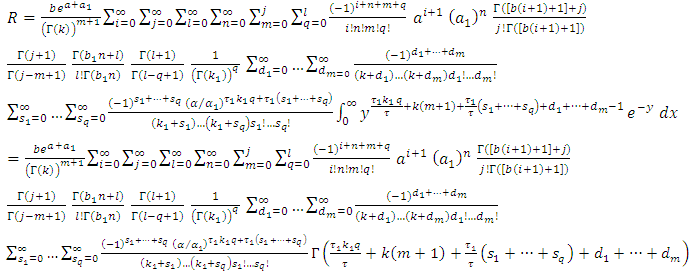
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML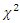 order statistics", Vol.3 (2008), No.3, pp.433-444.
order statistics", Vol.3 (2008), No.3, pp.433-444.