Ohochuku N. Stephen
Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Port Harcourt, Nigeria
Correspondence to: Ohochuku N. Stephen , Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The inherent properties of a regular polygon, viz equal sides and equal base angles, have been used with each side subtending the same angle (that is equal to the external angle) at the centre of the polygon to develop a method currently in use for the construction of any regular polygon. This paper reports of the use of the equal sides, equal base angles and equal angles (each of which is equal to half the external angle) subtended by the sides at the corner to generate new methods for the construction of a regular polygon. The harnessing of equal diagonals with the equal sides and equal exterior angle yielded another method of regular polygon construction and this is also presented here. These novel methods are less demanding, clear and straight forward compared to any existing methods requiring direct construction of base or external angle as a pre-requisite as in these new methods.
Keywords:
Polygon construction subtended angle diagonals
Cite this paper: Ohochuku N. Stephen , Constructing a Regular Polygon from the Angles Subtended by Its Base at Its Corner and through the Use of the Equality between Diagonals, Applied Mathematics, Vol. 7 No. 3, 2017, pp. 44-50. doi: 10.5923/j.am.20170703.02.
Article Outline
- 1. Introduction
- 2. Methodology
- 2.1. Construction of a Regular Polygon of Side AB by Division of Its Corner or Base Angle into n-2 Equal Parts, Illustrated with a 7-gon, Figure 4
- 2.2. Use of Angle Subtended at Corner being Half the External Angle to Construct a Regular Polygon, 7-gon Illustrated, Figure 5
- 2.3. Constructing a Regular Polygon of Side AB Using Equal Diagonals, 8-gon Illustrated, Figure 6
- 2.4. Application of Equal Division of a Base Angle into n-2 Equal Parts as a Template for Constructing Members of an n-gon, Illustrated with a Regular 5-gon, Figure 7
- 2.5. Other Uses of the Template
- 2.5.1. To Circumscribe a Given Regular n-gon in a Circle, Illustrated with a 6- and 7-gon
- 2.5.2. Inscribing an n-gon in a Given Circle, Illustrated with a 6- and 7-gon
- 2.6. Template from 360o/n: Use in Constructing Any Regular n-Polygon of Chosen Side
- 3. Results and Discussion
- 3.1. Proofs of Principles Applied in the new Methods
- 3.1.1. The Sides (Bases) of a regular Polygon Subtend Equal Angles at Any Corner of the Polygon
- 3.1.2. Subtended Angle at the Corner is Half The Exterior Angle, Figure 12
- 3.1.3. Equal Diagonals Subtend Equal Angles at the Centre of the Polygon, Figure 12, Illustrated with a 7-gon
- 3.1.4. Sides/Diagonals that are Parallel; Perpendicular Bisector of Any Diagonal Passes through the Centroid, Figure 13, Illustrated with 7- and 8-gon
- 3.2. Comments on the Constructions
- 3.2.1. Division of a Corner (Base) Angle into n-2 equal Parts
- 3.2.2. The construction of the external Angle of 7-gon as 6(60o/7) in place of 360o/7
- 3.2.3. Use of Equal Diagonals
- 3.3. Use of Template to Construct Members of n-Polygons and Inscribing Given n-gons in a Circle and Vice Versa
- 3.4. Summary of the Principles Applied in Constructing Regular Polygons by These New Methods
- 4. Conclusions
1. Introduction
A regular polygon as a plane geometric figure bound by three or more equal straight sides and with equal base/external angles [1, 2, 3a] are usually constructed using the above properties coupled with the equality of the angles subtended at the centre of the polygon by the sides each subtended angle being equal to the external angle. The comprehensive properties of any regular polygon are the following. As in figure 1a, (a) equal sides, (b) equal base/external angles, (c) a centroid (meeting point of the base bisectors, base angle bisectors and perpendicular base bisectors) which is also the centre of the polygon and the incentre and excentre for the inscribed and escribed circles, (d) each base subtends at the centre of the polygon the same value of angles each of which is equal to the exterior angle: As in figure 1b, (e) each base subtends the same measure of angle at any or same corner of the polygon, each subtended angle being half of the exterior angle, (f) equal diagonals have their respective termini separated by same number of corners, or equal diagonals subtend equal angles at the centre of the regular polygon, as in figure 1b (g) any pair of sides or pair of diagonals or a side and a diagonal that have equal number of sides/corners separating their respective terminals at the either ends are parallel, and as in figure 1a,b (h) the perpendicular bisectors of any side or diagonal passes through the centre of the polygon. Current methods using properties (a) to (d) end up inscribing the regular polygon in a circle of centre the same as the centroid and radius as AO, figure 1a, i.e. the distance from the corner along the base angle bisector to the centre of the polygon.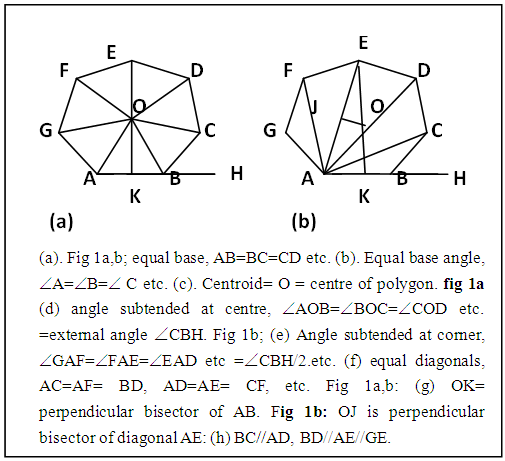 | Figure 1. Illustrating the Properties of a regular Polygon, with a Regular Heptagon |
There are other methods of constructing regular polygons. One method [3] copies the external angle n-2 times (n is the number of sides of the polygon) to each determined corner of the n-polygon or n-gon, figure 2. Others [4, 5], avoid the construction of the base angle by constructing the polygon through the use of circles. A few of the general methods [5, 6] fall within this category. The many methods that circumvent the use of base or external angle arose from the fact that many base or external angles of some regular polygons are not easily constructed. This difficulty has however been removed by the introduction of methods that equipartition plane angles into any number of parts [7]. | Figure 2. Regular Polygon Construction by copying external Angle illustrated with Hexagon |
The back bone of the current method of constructing a regular polygon by inscribing it in a circle is properties (a) to (d) listed above. Properties (e) and (f) i.e. the sides subtending equal angles at a corner, each of the subtended angle being equal to half the external angle and equal diagonals have their respective termini separated by equal number of corners could also be harnessed with equal base or external angle to derive methods for the construction of any regular polygon. There is thus the necessity to look for such methods for regular polygon construction. This paper reports of methods that use these properties to construct any regular polygon.
2. Methodology
From figure 3, a regular n-gon has n-2 triangles when each corner is joined to a common corner thus creating n-2 equal angles at that common corner. These equal angles, at that corner, sum up to the base angle. That is the corner (base angle) is divided into n-2 equal parts. Also each of the n-2 subtended angles is equal to half the external angle. The common arms of neighbouring subtended angles are the n-3 diagonals emerging from a corner to other respective corners. To use the n-2 equal angles of a corner to construct a regular polygon, the base angle will be constructed and divided into n-2 equal parts. The respective n-3 straight lines separating neighboring angles will be the respective straight lines housing each of the n-3 diagonals. The other end of each of the diagonals can readily be fixed.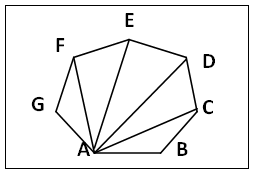 | Figure 3. Shows n-2 equal Angles subtended by n-2 sides at a corner, 7-gon illustrated |
To utilize the external angle being twice the subtended angle to construct a regular polygon, the external angle will be constructed, bisected and the half angle copied to a constant point on a straight line. Repeating this n-2 times along the appropriate arm of the previously copied half angle gives the n-3 straight lines housing each of the diagonals, of which the respective other ends can be easily fixed.To use the equal diagonals requires constructing the exterior angle, marking out the sides AB and BC of the polygon; the diagonal AC is one of those diagonals to use with a side of the polygon to determine the terminus of each of the other diagonals emerging from a common corner. The methods below give the details of the procedures.
2.1. Construction of a Regular Polygon of Side AB by Division of Its Corner or Base Angle into n-2 Equal Parts, Illustrated with a 7-gon, Figure 4
(a). On a straight line PQ mark the given side AB, figure 4.(b). Centre B and with any convenient radius draw a semicircle that cuts PQ at H and J. Partition the semicircle (i.e. the 180°, the straight line angle) into seven equal arcs (or angles) at points K, L, M, N, O and R by the working radius method [7]. Join BL producing to S, ∠SBQ is the exterior angle and ∠PBS is the base angle of the polygon (7-gon). Join B to M, N, O, and R producing each line upwards. These n-3 produced lines house the n-3 diagonals the ends of which are to be respectively fixed as shown below.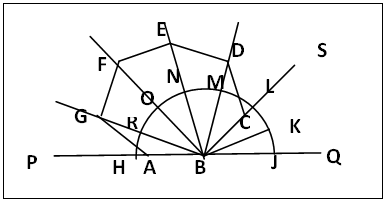 | Figure 4. Construction of a regular Polygon using n-2 equal subtended Angles at a corner |
(c). Centre B radius AB cut BS at C.Centre C same radius cut BM produced at D, join CD. Centre D same radius cut BN produced at E, join DE.Centre E same radius cut BO produced at F, join EF.Centre F same radius cut BR produced at G, join FG.Centre G same radius cut BP at A join GA. ABCDEFG is the required polygon (7-gon).
2.2. Use of Angle Subtended at Corner being Half the External Angle to Construct a Regular Polygon, 7-gon Illustrated, Figure 5
(a). On a straight line PQ mark the given side AB, figure 5. At B on BQ construct the exterior angle 513/ 7 o using 513/ 7 o = 60o – 84/7o = 60o – 60o/7 = 6(60o/7) by the working radius method [7]. That is equally dividing 60o by 7 and taking six parts as the external angle of the regular heptagon. Let ∠JBQ, figure 5, be the exterior angle and BH its bisector.(b). Copy ∠HBQ to point B on BJ to get ∠KBJ = ∠HBQ.Copy ∠HBQ to point B on BK to get ∠LBK = ∠HBQ.Copy ∠HBQ to point B on BL to get ∠MBL = ∠HBQ.Copy ∠HBQ to point B on BM to get ∠NBM = ∠HBQ.Copy ∠HBQ to point B on BN to get ∠PBN = ∠HBQ.(c). Centre B radius AB cut BJ at C.Centre C same radius cut BK at D, join CD.Centre D same radius cut BL at E, join DE.Centre E same radius cut BM at F, join EF.Centre F same radius cut BN at G, join FG.Centre G same radius cut BP at A, join GA.ABCDEFG is the 7-gon.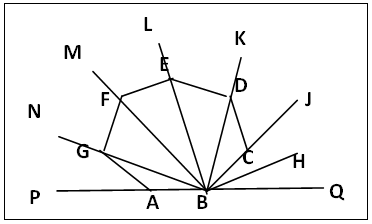 | Figure 5. Construction of a regular Polygon using Angle subtended at corner equals half external Angle |
2.3. Constructing a Regular Polygon of Side AB Using Equal Diagonals, 8-gon Illustrated, Figure 6
(a). On a straight line PQ mark the given side AB, figure 6.(b). Centre B construct ∠JBQ = 45° the exterior angle of a regular 8-gon.(c). Centre B radius AB cut BJ at C.Centre C radius AB swing arc above C, centre B radius AC cut arc at D, join CD.Centre D radius AB swing arc above D, centre C radius AC cut arc at E, join DE.Centre E radius AB swing arc left of E, centre D radius AC cut arc at F, join EF.Centre F radius AB swing arc left of F, centre E radius AC cut arc at G, join FG. 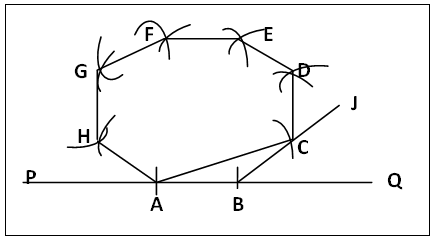 | Figure 6. Construction of a regular polygon using Equality of Diagonals connecting corners separated with same number of corners |
Centre G radius AB swing arc below G, centre F radius AC cut arc at H, join GH and HA. ABCDEFGH is the required regular polygon (8-gon). Although diagonal AC (equals BD=CE etc) as radius with center C and radius AB with centre D were used to locate corner E, diagonal AD with centre B and diagonal AC with centre C can also be used to locate E. Such practices, whenever such diagonals and centres are available during the construction, are helpful.
2.4. Application of Equal Division of a Base Angle into n-2 Equal Parts as a Template for Constructing Members of an n-gon, Illustrated with a Regular 5-gon, Figure 7
(a). On a straight line PQ mark point A. At point A construct the base angle TAQ of a regular 5-gon divided into three (i.e. n-2) equal parts and having two (i.e. n-3) straight lines AR and RS, figure 7a, housing the two n-3 diagonals, by any of the methods in sections 2.1 or 2.2. Produce the straight lines housing the diagonals upwards respectively. If section 2.3 is used, point A is joined to the appropriate terminals C and D and produced to R and S respectively, dotted lines figure 7b. The angle, ∠TAQ, divided equally into three (n-2) parts and the straight lines AR and AS housing the two (n-3) diagonals form the template for a 5-gon.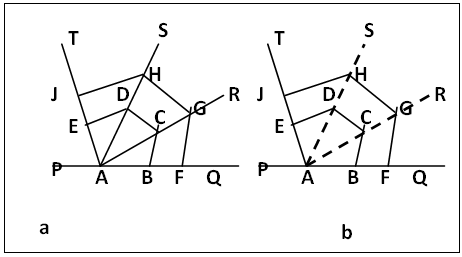 | Figure 7. Use of Template to draw polygons of same family |
(b). To draw a regular 5-gon of side 10 mm: centre A, radius 10mm cut AQ at B; centre B, same radius, cut AR at C; centre C, same radius cut AS at D; centre A same radius, cut AT at E. ABCDE is a regular 5-gon of side 10 mm.(c). To construct a regular 5-gon of side 20 mm, centre A, radius 20 mm cut AQ at F; centre F, same radius, cut AR at G; centre G, same radius cut AS at H; centre H same radius, cut AT at J. AFGHJ is a regular 5-gon of side 20 mm.By similar procedure on the template of any regular n-gon, an n-gon of chosen side can be readily be constructed by this process.
2.5. Other Uses of the Template
2.5.1. To Circumscribe a Given Regular n-gon in a Circle, Illustrated with a 6- and 7-gon
(a). Draw the 6-gon, figure 8a, and 7-gon, figure 8b. Draw the diagonals as shown with the labeling. The diagonals meeting in one corner A with the two arms of the base angle A form the template.(b). For even n, figure 8a: bisect the central diagonal AD at O, centre O, radius OA draw a circle that circumscribes the n-gon.(c). For odd n, figure 8b: let the perpendicular bisectors of the longer sides of the central isosceles triangle meet at O. Centre O, radius OA circumscribe the n-gon.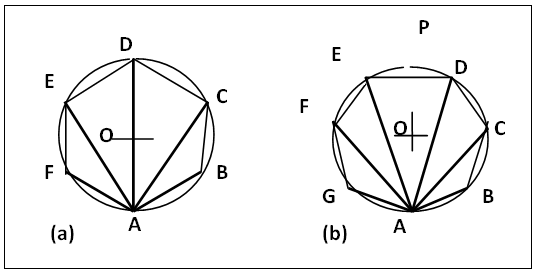 | Figure 8. Use of Template in circumscribing a given n-gon, 6- and 7-gon illustrated |
2.5.2. Inscribing an n-gon in a Given Circle, Illustrated with a 6- and 7-gon
(a). Construct at point A, the template of the n-gon either by methods in sections 2-1 to 2.3 or by any method of choice, figure 9a for even n and figure 9b for odd n and with their lettering. (b). For even n, figure 9a: Centre A, radius that of the given circle, cut the central line AP at O. Centre O, radius OA, draw the circle that cuts template lines at B, C, D, E and F, join these neighboring points. ABCDEF is the inscribed n-gon in a given circle.(c). For odd n, figure 9b: Let AP be the bisector of the central angle ∠DAE. Centre A, radius that of the given circle cut AP at O. Centre O radius OA draw a circle that cuts the template lines at B, C, D, E, F and G, join these neighboring points. ABCDEFG is the n-gon inscribed in a given circle. 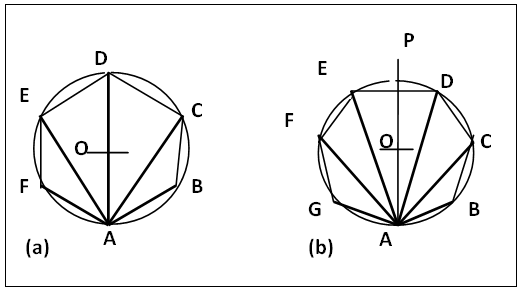 | Figure 9. Use of Template in inscribing an n-gon in a given Circle, 6- and 7-gon illustrated |
2.6. Template from 360o/n: Use in Constructing Any Regular n-Polygon of Chosen Side
The orthodox method of constructing a regular n-gon uses 360o/n subtended by each side at the centre of the polygon. The template from this consists of radial lines separating equal 360o/n and having common apex, O, which is the centre of the polygon, figure 10. This template when used to construct an n-gon gives an n-gon with side to be measured or calculated, excepting the 6-gon whose side is equal to the radius of the circumscribing circle. A new method using this template to construct any n-gon of chosen side length is reported here and called the “Tee- Square-Method” (TSM). The procedure is as follows, figure 10 with the lettering.(a). Draw the template of the n-gon (5-gon illustrated), with the radial lines OA, OB, OC, OD, and OE produced outwards, figure 10.(b). ON bisects ∠QOM, QR is a straight line longer than the chosen side length (ST) and cuts ON perpendicularly at P.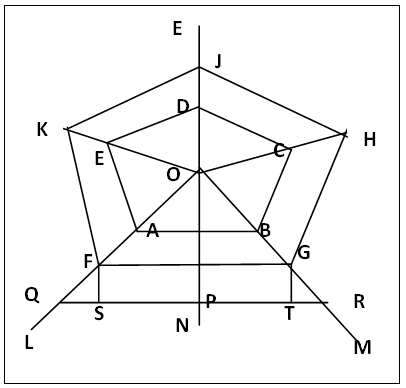 | Figure 10. Use of 360o/n Template to construct an n-gon of chosen Side Length |
Centre P, radius half of the chosen base length (ST), cut PQ at S and PR at T.(c). Erect perpendiculars at S and T to cut OL at F and OM at G respectively. Centre O, radius OF = OG, cut the other radial lines at H, J, and K. Join FG, GH, HJ, JK and KF to get the n-gon (5-gon) FGHJK of known side ST = FG.
3. Results and Discussion
3.1. Proofs of Principles Applied in the new Methods
The new methods of constructing a regular polygon are based on the hardly or rarely mentioned properties of the regular polygon and they have not been applied to generating methods for the construction of regular polygons. So it is necessary to show proof of any principle utilized in the methods of construction.
3.1.1. The Sides (Bases) of a regular Polygon Subtend Equal Angles at Any Corner of the Polygon
Every regular polygon is a cyclic regular polygon. That is every regular polygon can be inscribed in a circle and its sides subtend the same angles at the centre of the circle and also equal angles at any point (which can be its corner too) on the circumference of the circumscribing circle. This is not true for any other cyclic polygon, figure 11. Therefore all the n-2 sides of a regular polygon subtend equal angles at any corner or one corner. That is a corner or base angle (angle A say, figure 11a) is divided into n-2 equal parts by n-2 sides i.e. ∠EAD = ∠DAC = ∠CAB = ∠EDA = ∠ADB etc.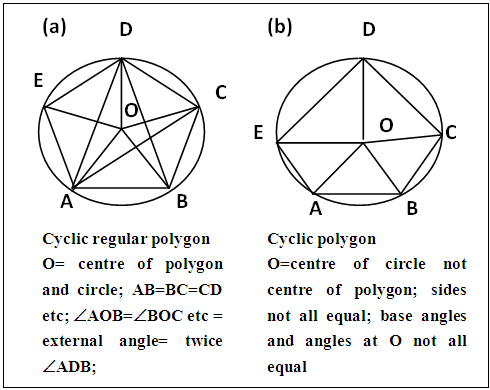 | Figure 11. Comparison of cyclic regular polygon and cyclic polygon illustrated with pentagon |
3.1.2. Subtended Angle at the Corner is Half The Exterior Angle, Figure 12
Consider ΔGBA, figure 12, BA = AG (sides of regular polygon), hence ΔGBA is isosceles; ∠AGB = ∠ABG (base angles of isosceles triangle); hence ∠AGB + ∠GBA = ∠GAP (sum of two interior angles equals one exterior angle), i.e. 2∠AGB = 2∠GBA = ∠GAP (the exterior angle). Hence each of the angle subtended at the corner is half of the external angle. 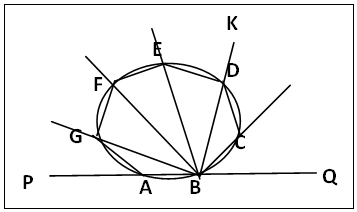 | Figure 12. Illustrating the Proofs of the Principles used in the new Methods |
3.1.3. Equal Diagonals Subtend Equal Angles at the Centre of the Polygon, Figure 12, Illustrated with a 7-gon
In ΔBGA and ΔBDC, figure 12, BA = AG = BC = CD (sides of a regular polygon); ∠A = ∠C, (base angles of a regular polygon) so ΔBGA and ΔBDC are congruent (SAS). Hence BG and BD are equal and they are diagonals with their respective termini B and G, B and D separated by two sides (or one corner or as equal chords to the circumscribing circle they subtend equal angles at the centre). Also consider the quadrilaterals ABFG and BCDE, figure 12, BA = AG = GF = BC = CD = DE (sides of a regular polygon); ∠A = ∠G = ∠C = ∠D (base angles of a regular polygon), ∠ABF = ∠BFG = ∠CBE = ∠DEB (sum of angles subtended at corners or points at the circumference by two adjacent sides of a regular polygon). Hence quadrilaterals ABFG and BCDE are congruent with the diagonals BF = BE. By similar considerations, it can be shown that in general diagonals with respective termini separated by the same number of corners or sides of a regular polygon are equal or that equal diagonals subtend equal angles at the centre.
3.1.4. Sides/Diagonals that are Parallel; Perpendicular Bisector of Any Diagonal Passes through the Centroid, Figure 13, Illustrated with 7- and 8-gon
In figure 13, O is the centre of the regular n-gon (7- and 8-gon). OJ is the perpendicular bisector of CD. The lettering in the figure will be used in the discussion.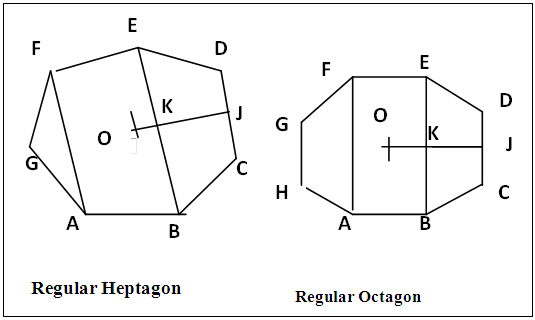 | Figure 13. Sides/Diagonals that are parallel; Perpendicular bisector of Diagonal passes through the Centre of polygon |
Parallel sides/diagonals: In quadrilaterals BCJK and KJDE, BC = DE (sides of regular polygon), CJ = JD (by construction), JK is common, ∠C = ∠D (base angles of regular polygon), ∠KBC = ∠KED (sum of equal angles subtended at a corner by two equal adjacent sides of a polygon), ∠KJC = ∠KJD = 90° (by construction). Hence quadrilateral BCJK is congruent to quadrilateral KJDE. Therefore BK = KE, ∠BKJ = ∠JKE = 90° and JO bisects BE perpendicularly at K. Therefore BE//CD. It can also be shown that BE//AF.Perpendicular bisector of any diagonal passes through the centre of the polygonIt is shown above that JO bisects BE perpendicularly at K. That is the perpendicular bisector of diagonal BE passes through O, this is true for every other diagonal. As every regular polygon is a cyclic regular polygon, its sides and diagonals are chords of the circumscribing circle and perpendicular bisector of a chord passes through the centre of the circle. It is the principle used to determine the excentre of the circumscribing circle in section 2.5.2, figure 9b.
3.2. Comments on the Constructions
3.2.1. Division of a Corner (Base) Angle into n-2 equal Parts
In section 2.1, figure 4 illustrated with a 7-gon, the base angle of a regular 7-gon was constructed through the external angle 513/7o = 360o/7 = 2(180o/7) and taking two parts as the external angle. The remaining five (i.e. n-2) parts give the base angle. The method applied in section 2.1 requires the equal division of the base angle into n-2 parts (for constructing any regular polygon) and this n-2 parts are obtained in situ during the construction of the base angle via the external angle i.e. ‘killing two birds with one stone’. This makes the construction of regular polygons by this method very easy.
3.2.2. The construction of the external Angle of 7-gon as 6(60o/7) in place of 360o/7
The new method applied here requires the external angle not the internal angle. So instead of constructing the external angle of a 7-gon (513/7o) through 360o/7 which will also give the base angle, an alternative which is dividing 60o by seven and taking six parts is chosen. This alternative permits complete demonstration of this particular new method that uses subtended angle equals half the external angle. The use of 6(60o/7) or its equivalent in other polygons permits the use of this method in cases where the external angle can be constructed by bisection or other methods e.g. 45° for 8-gon, 40o = 2(60o/3) = external angle of a regular 9-gon and so on. Of course if 360o/7 = 2(180o/7) is used, five units of the quotient will be discarded.
3.2.3. Use of Equal Diagonals
This method needs only the external angle which should be constructed by the most convenient method; otherwise, as applicable to other new methods, the external angle will be constructed elsewhere and copied to the appropriate point. This particular method that uses equal diagonals is the simplest of all the three methods. Once the external (or base) angle is constructed, three succeeding sides HA, AB and BC of the regular polygon (8-gon in this case) are fixed so also diagonals HC and AC, figure 6. The use of the radii AB and AC (or HC and AC) with the appropriate centres fixes the other respective corners of the polygon, the alternative use of HC and AC or their equivalents whenever possible simplifies the work. The method of equal diagonals is devoid of numerous construction lines.
3.3. Use of Template to Construct Members of n-Polygons and Inscribing Given n-gons in a Circle and Vice Versa
Every regular n-gon has two templates: one as the base angle divided equally into n-2 parts, figure 14a and a second one as the angle of revolution at its centre divided into n equal parts, figure 14b, all thick lines, for 5-gon as stated in section 2.6. Both templates can be used to enlarge or diminish a given n-gon and thus are additional methods to parallel line method [3]. | Figure 14. Templates of an n-gon, illustrated with a 5-gon |
The first template can be used to construct or enlarge or shrink a regular n-gon (or 2n-gon with angle bisection) to a pre-determined side length and this is peculiar to it. The second template from presently current methods of construction cannot be used to construct or enlarge or shrink an n-gon (or 2n-gon by angle bisection) to a pre-determined side length (except a regular 6-gon because 6-gon side is the same as the radius of the circumscribing circle), unless the new “Tee-Square-Method, TSM” which is now being introduced is applied.The use of template in inscribing a given n-gon in a circle and vice versa is additional methods to the current procedures. The applications show that whatever that can be done with the template derived from 360o/n can also be performed with that from base angle divided by n-2, and at times with better advantage. The methods used in illustrating the new principles are the basic procedures; other variation in the procedures can be applied where they reduce the number of steps as in the copying of angles.
3.4. Summary of the Principles Applied in Constructing Regular Polygons by These New Methods
The principles used are the following. (i). A regular n sided polygon has equal sides and equal base angles.(ii). The sides subtend n-2 equal angles at any corner of the polygon; i.e. a corner or base angle is the sum of the equal n-2 subtended angles. (iii). Each subtended angle is half the external angle of the regular polygon.(iv) Only n-3 corners have their diagonals meet at a common corner.(v). Diagonals terminating at corners that are separated by the same number of sides or corners are equal in length or equal diagonals subtend equal angles at the centre of the polygon.(vi). Perpendicular bisector of any diagonal passes through the centre of the polygon.
4. Conclusions
The new methods reported here for the construction of regular polygons are novel methods and they are additions to the current general methods in use. They deviate slightly from the methods in vogue. They are easy, clear, without complexities and straight forward. They are perfectly general methods. The uses of their templates including the ‘Tee-Square-Method’ are new development in regular polygon constructions as any regular polygon can now be readily and easily constructed by various methods and with chosen side length. These are important advancements.
References
| [1] | Macrea M F, Kalejaiye A O, Chima Z I, Garba G U, Channon J B, MacLeish Smith A, and Head H C. 2008. New General Mathematics for senior Secondary Schools UBE Edition. Pearson Educational Ltd, Edinburh Gate, Harlow, Essex CM 20 2EJ, England, p9. |
| [2] | Bailey, Day, FREY, Howard, Hutchens, Mclain, Moore-Harris, Olt, Pelfrey, Prie, Vielhaber, and Willard. Mathematics: Applications and Concepts Course 2. Florida Edition, fl.msmaths.net McGraw Hill Glencoe. New York. Chapter 10-7 pp446-447. |
| [3] | Elekwa I, Bamiro O A, Oluyide A O, Ladoye D l, Nurudeen A, Akuru I O. 2011.Basic Technology for Junior Secondary Schools Book 2. Evans Brothers (Nigeria Publishers) Ltd, Jericho Road, Ibadan, Nigeria, (a) p61, (b) pp72-73. |
| [4] | Comparative Education Study and Adaptation Centre, CESAC. 1986. Introductory Technology for Junior Secondary Schools Text book 2, p16. |
| [5] | Ohochuku, N. Stephen. 2017. A General Method of Constructing polygons from a Square. American Journal of Mathematics and Statistics 7(1), pp32 – 37. http:/journal.sapub.org/ajms. |
| [6] | Ohochuku, N. S. 2016. Methods of Constructing Regular Polygons Suitable for Introductory Lessons. American Journal of Mathematics and Statistics 6(6), http:/journal.sapub.org/ajms. |
| [7] | Ohochuku, N. S. 2015. Equipartition of Plane Geometric Angles into any Number of Parts. Journal of Applied Mathematics, 5(4). Pp84 – 87. http://journal.sapub.org/am. |

















 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML