-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2017; 7(3): 39-43
doi:10.5923/j.am.20170703.01

Oscillation Theorems for Linear Neutral Impulsive Differential Equations of the Second Order with Variable Coefficients and Constant Retarded Arguments
Ubon Akpan Abasiekwere, Imoh Udo Moffat
Department of Mathematics and Statistics, University of Uyo, Uyo, Nigeria
Correspondence to: Ubon Akpan Abasiekwere, Department of Mathematics and Statistics, University of Uyo, Uyo, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper deals with the oscillations of a class of second order linear neutral impulsive ordinary differential equations with variable coefficients and constant retarded arguments. Here, we obtain sufficient conditions ensuring the oscillation of all solutions. Examples are provided to illustrate the abstract results.
Keywords: Differential equations, Impulsive, Oscillations, Retarded arguments, Second order
Cite this paper: Ubon Akpan Abasiekwere, Imoh Udo Moffat, Oscillation Theorems for Linear Neutral Impulsive Differential Equations of the Second Order with Variable Coefficients and Constant Retarded Arguments, Applied Mathematics, Vol. 7 No. 3, 2017, pp. 39-43. doi: 10.5923/j.am.20170703.01.
1. Introduction
- Since Sturm’s famous memoir in the 17th century, it is observed that a great deal of interest has been focused on the behaviour of solutions of ordinary and delay differential equations in spite of the existence of extensive literature in these fields ([10], [12], [20], [22]). Delay differential equations has applications in the modeling of complex biological systems, population dynamics, neural network, etc ([19], [21], [23]). Stochastic functional differential equations with state-dependent delay, which have many important applications in mathematical models of real phenomena, is not left out in this seemingly unending quest for knowledge ([15], [16], [17], [18]). Still more interesting, the theory of impulsive differential equations has brought in yet another dimension to the whole scenario and has helped to usher in a new body of knowledge for further considerations. The effects of these new inputs can be observed in the study of oscillatory properties of impulsive differential equations with deviating arguments as well as the investigation of neutral impulsive differential equations which have recently captured the attention of many applied mathematicians as well as other scientists around the world. In 1989 the paper of Gopalsamy and Zhang [11] was published, where the first investigation on oscillatory properties of impulsive differential equations was carried out. Since then, several authors including Butler [2], Lakshmikantham et al. [4], Travis [5], Wong [6] and Ladde et al. [12] have since studied oscillations of second-order ordinary differential equations. Lately, the pioneering efforts of Isaac and Lipcsey ([7], [8], [9], [13]) in identifying some of the essential oscillatory and non-oscillatory conditions of neutral impulsive differential equations of the first order is also worth commending. However, relatively less attention has been given to oscillations of second-order neutral delay differential equations with impulses.This work therefore is concerned with the problem of oscillation of all solutions of a class of second order linear impulsive differential equations with variable coefficients and constant delays. The theory of oscillations of neutral impulsive differential equations is gradually occupying a central place among the theories of oscillations of impulsive differential equations. This could be due to the fact that neutral impulsive differential equations play fundamental roles in the present drive to further develop information technology. Indeed, neutral differential equations appear in networks containing lossless transmission lines (as in high-speed computers where the lossless transmission lines are used to interconnect switching circuits).Impulsive differential equations are adequate mathematical models for description of evolution processes characterized by the combination of a continuous and jumps change of their state:Now, let an evolution process evolve in a period of time
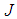 in an open set
in an open set 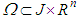 and let the function
and let the function 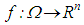 be at the least a continuous mapping fulfilling local Lipchitzian condition in
be at the least a continuous mapping fulfilling local Lipchitzian condition in 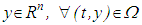 . Let the real numerical sequence
. Let the real numerical sequence 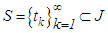 be increasing without finite accumulation point such that
be increasing without finite accumulation point such that 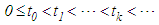 with
with 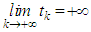 ,. The points
,. The points 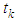 are called moments of impulse effect. Then the governing second order impulsive differential equation is of the form
are called moments of impulse effect. Then the governing second order impulsive differential equation is of the form 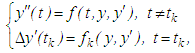 | (1.1) |
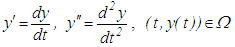 ,
, 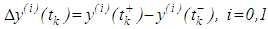 and
and 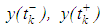 represent the left and right limits of
represent the left and right limits of 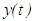 at
at 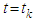 , respectively. For the sake of definiteness, we shall suppose that the functions
, respectively. For the sake of definiteness, we shall suppose that the functions 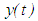 and
and 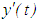 are continuous from the left at the points
are continuous from the left at the points 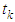 such that
such that 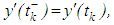
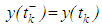 .For the description of the continuous change of such processes ordinary differential equations are used, while the moments and the magnitude of the change by jumps are given by the jump conditions. Now, in the case of unfixed moments of impulse effects, the impulse points may be time and state dependent, that is,
.For the description of the continuous change of such processes ordinary differential equations are used, while the moments and the magnitude of the change by jumps are given by the jump conditions. Now, in the case of unfixed moments of impulse effects, the impulse points may be time and state dependent, that is, 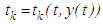 . When the function
. When the function 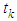 depends on the state of the system (1.1), then it is said to have impulses at variable times. This is reflected in the fact that different solutions will tend to undergo impulses at different times.In this paper, we shall restrict ourselves to the investigation of properties of the solutions of impulsive differential equations with fixed moments of impulse effect, that is, the moments of jump are previously fixed. Our equation under consideration is of the form
depends on the state of the system (1.1), then it is said to have impulses at variable times. This is reflected in the fact that different solutions will tend to undergo impulses at different times.In this paper, we shall restrict ourselves to the investigation of properties of the solutions of impulsive differential equations with fixed moments of impulse effect, that is, the moments of jump are previously fixed. Our equation under consideration is of the form 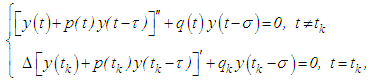 | (1.2) |
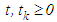 . The second order neutral delay impulsive differential equation (1.2) is a differential system comprising a second-order differential equation and its impulsive conditions in which the highest-order derivative of the unknown function appears in the differential equation both with and without delay.Let
. The second order neutral delay impulsive differential equation (1.2) is a differential system comprising a second-order differential equation and its impulsive conditions in which the highest-order derivative of the unknown function appears in the differential equation both with and without delay.Let  . We say that a real valued function
. We say that a real valued function 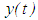 is the solution of equation (1.2) if there exists a number
is the solution of equation (1.2) if there exists a number 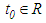 such that
such that 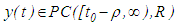 , the function
, the function 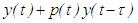 is twice continuously differentiable for
is twice continuously differentiable for 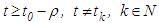 and
and 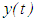 satisfies equation (1.2) for all
satisfies equation (1.2) for all 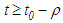 .Without further mentioning, we will assume throughout this paper that every solution
.Without further mentioning, we will assume throughout this paper that every solution 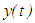 of equation (2.1) that is under consideration here, is continuous from the left and is nontrivial. That is,
of equation (2.1) that is under consideration here, is continuous from the left and is nontrivial. That is, 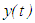 is defined on some half-line
is defined on some half-line 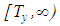 and
and 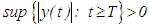 for all
for all 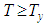 . Such a solution is called a regular solution of equation (2.1). We say that a real valued function
. Such a solution is called a regular solution of equation (2.1). We say that a real valued function 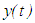 defined on an interval
defined on an interval 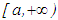 fulfills some property finally, if there exists a number
fulfills some property finally, if there exists a number 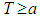 such that
such that 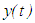 has this property on the interval
has this property on the interval 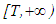 .Definition 1.4 The solution
.Definition 1.4 The solution 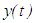 of an impulsive differential equation is said to bei) finally positive (finally negative) if there exist
of an impulsive differential equation is said to bei) finally positive (finally negative) if there exist 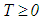 such that
such that 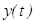 is defined and is strictly positive (negative) for
is defined and is strictly positive (negative) for 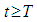 [8];ii) non-oscillatory, if it is either finally positive or finally negative; andiii) oscillatory, if it is neither finally positive nor finally negative ([1], [9]).In the sequel, all functional inequalities that we write are assumed to hold finally, that is, for all sufficiently large t.
[8];ii) non-oscillatory, if it is either finally positive or finally negative; andiii) oscillatory, if it is neither finally positive nor finally negative ([1], [9]).In the sequel, all functional inequalities that we write are assumed to hold finally, that is, for all sufficiently large t.2. Statement of the Problem
- We are concerned with the oscillatory properties of the second order linear neutral delay impulsive differential equation with variable coefficients and constant deviating arguments of the form
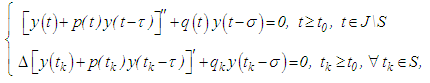 | (2.1) |
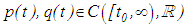 and
and 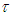 and
and 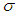 are non-negative real numbers. Our aim is to establish some sufficient conditions for every bounded solution of equation (2.1) to be oscillatory. Throughout this study, we shall assume the following:C2.1:
are non-negative real numbers. Our aim is to establish some sufficient conditions for every bounded solution of equation (2.1) to be oscillatory. Throughout this study, we shall assume the following:C2.1: 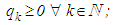 C2.2:
C2.2: 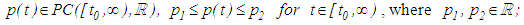 C2.3:
C2.3: 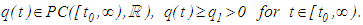 Here, we demonstrate how well-known mathematical techniques and methods (due to studies by Bainov and Simeonov [1]), after suitable modifications, is extended in proving an oscillation theorem for impulsive delay differential equations. We shall restrict ourselves to the study of impulsive differential equations for which the impulse effects take place at fixed moments of time
Here, we demonstrate how well-known mathematical techniques and methods (due to studies by Bainov and Simeonov [1]), after suitable modifications, is extended in proving an oscillation theorem for impulsive delay differential equations. We shall restrict ourselves to the study of impulsive differential equations for which the impulse effects take place at fixed moments of time 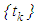 .Lemma 2.1 and Lemma 2.2, which are essential in carrying out our investigation are impulsive extensions of the work done by Grammatikopoulos et al [14] and Ladas and Stavroulakis [10], respectively, in their quest to find sufficient conditions for oscillation of all solutions of a type of neutral delay ordinary differential equations.Lemma 2.1: Assume conditions C2.1—C2.3 satisfied and let
.Lemma 2.1 and Lemma 2.2, which are essential in carrying out our investigation are impulsive extensions of the work done by Grammatikopoulos et al [14] and Ladas and Stavroulakis [10], respectively, in their quest to find sufficient conditions for oscillation of all solutions of a type of neutral delay ordinary differential equations.Lemma 2.1: Assume conditions C2.1—C2.3 satisfied and let 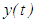 be a finally positive solution of equation (2.1). Set
be a finally positive solution of equation (2.1). Set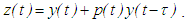 | (2.2) |
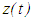 and
and 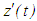 are strictly monotone and either
are strictly monotone and either 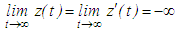 | (2.3) |
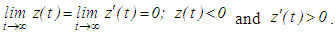 | (2.4) |
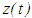 is finally negative.b) Assume that
is finally negative.b) Assume that 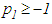 , then condition (2.4) holds. In particular,
, then condition (2.4) holds. In particular, 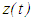 is bounded. Proof: (a) From equation (2.1), we have that
is bounded. Proof: (a) From equation (2.1), we have that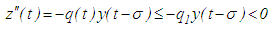 and
and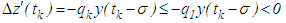 | (2.5) |
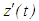 is a strictly decreasing function of t and so
is a strictly decreasing function of t and so 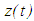 is a strictly monotone function. From the above observations it follows that either
is a strictly monotone function. From the above observations it follows that either 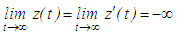 or
or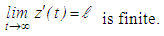 | (2.6) |
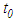 to t with
to t with 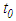 sufficiently large, and letting
sufficiently large, and letting 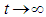 , we obtain
, we obtain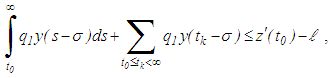 ,which implies that
,which implies that 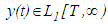 and so
and so 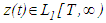 , where
, where 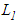 is the space of all Lebesgue integrable functions on
is the space of all Lebesgue integrable functions on 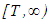 . Since
. Since 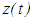 is monotone, it follows that
is monotone, it follows that 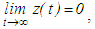 | (2.7) |
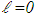 . Finally, by equations (2.7) and (2.6) with
. Finally, by equations (2.7) and (2.6) with 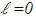 and the decreasing nature of
and the decreasing nature of 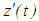 , we conclude that
, we conclude that 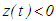 and
and 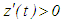 .c) By contradiction, we assume condition (2.4) was false, then from condition (2.3), it would follow that
.c) By contradiction, we assume condition (2.4) was false, then from condition (2.3), it would follow that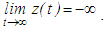 | (2.8) |
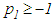 and
and 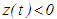 , we obtain
, we obtain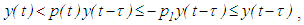 which implies that
which implies that 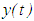 is bounded, contradicting condition (2.8) and proving that condition (2.4) is fulfilled. This, therefore, completes the proof of Lemma 2.1.We now present another lemma which will be useful in the discussion of the main results.Lemma 2.2: Assume that
is bounded, contradicting condition (2.8) and proving that condition (2.4) is fulfilled. This, therefore, completes the proof of Lemma 2.1.We now present another lemma which will be useful in the discussion of the main results.Lemma 2.2: Assume that 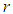 and
and 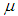 are positive constants such that
are positive constants such that 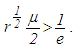 Then the differential inequality
Then the differential inequality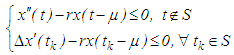 has no finally negative bounded solution.
has no finally negative bounded solution.3. Main Results
- The following theorems are the impulsive extensions of Theorem 3.1.2 and Theorem 3.1.3 of the monograph by Bainov and Mishev [3].Theorem 3.1: Consider the neutral delay impulsive differential equation (2.1) and assume conditions C2.1—C2.3 satisfied. Furthermore, assume that
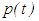 is not finally negative. Then every solution of equation (2.1) oscillates.Proof: By contradiction, we assume that
is not finally negative. Then every solution of equation (2.1) oscillates.Proof: By contradiction, we assume that 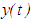 is a finally positive solution of equation (2.1). Set
is a finally positive solution of equation (2.1). Set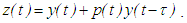 We can see here that
We can see here that 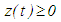 finally. However, by Lemma 2.1(a),
finally. However, by Lemma 2.1(a), 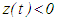 finally. This contradicts the statement of the theorem that
finally. This contradicts the statement of the theorem that 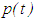 is not finally negative, and therefore, completes the proof of Theorem 3.1.The following illustration will enhance clarity:Example 3.1: Consider the equation
is not finally negative, and therefore, completes the proof of Theorem 3.1.The following illustration will enhance clarity:Example 3.1: Consider the equation 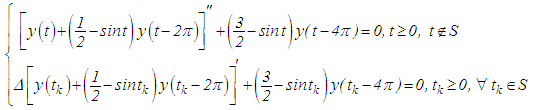 | (3.1) |
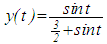 is an oscillating solution.This illustration shows that if the hypothesis of
is an oscillating solution.This illustration shows that if the hypothesis of 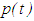 not being finally negative in Theorem 3.1 is violated, the result may be wrong.Example 3.2: Consider the equation
not being finally negative in Theorem 3.1 is violated, the result may be wrong.Example 3.2: Consider the equation 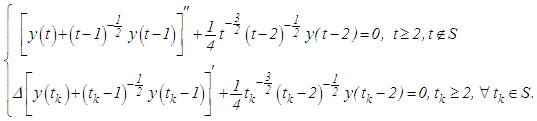 All assumptions of Theorem 3.2, except (ii) are satisfied. Note, however, that
All assumptions of Theorem 3.2, except (ii) are satisfied. Note, however, that 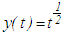 is a non-oscillatory solution.Theorem 3.2: Assume that conditions C2.1—C2.3 are satisfied with
is a non-oscillatory solution.Theorem 3.2: Assume that conditions C2.1—C2.3 are satisfied with 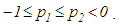 | (3.2) |
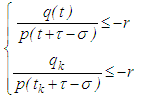 | (3.3) |
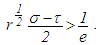 | (3.4) |
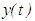 is a finally positive solution of equation (2.1). Set
is a finally positive solution of equation (2.1). Set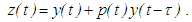 Then a direct substitution shows that
Then a direct substitution shows that 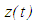 is a twice piece-wise continuously differentiable solution of the neutral delay impulsive differential equation
is a twice piece-wise continuously differentiable solution of the neutral delay impulsive differential equation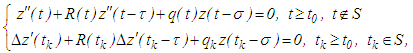 | (3.5) |
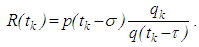 From equation (2.1) we have that
From equation (2.1) we have that 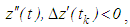 | (3.6) |
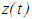 is a finally negative bounded function. Using condition (3.6), equation (3.5) yields
is a finally negative bounded function. Using condition (3.6), equation (3.5) yields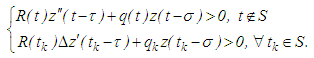 Hence, in view of equation (3.3), we obtain
Hence, in view of equation (3.3), we obtain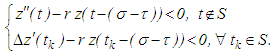 But due to condition (3.4), Lemma 2.2 implies that it is impossible for this inequality to have a finally negative bounded solution, which is a contradiction. This completes the proof of Theorem 3.2.The following illustration shows that if the condition
But due to condition (3.4), Lemma 2.2 implies that it is impossible for this inequality to have a finally negative bounded solution, which is a contradiction. This completes the proof of Theorem 3.2.The following illustration shows that if the condition 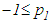 of Theorem 3.2 is violated, the result may not be true.Example 3.3: Consider the neutral delay impulsive differential equation
of Theorem 3.2 is violated, the result may not be true.Example 3.3: Consider the neutral delay impulsive differential equation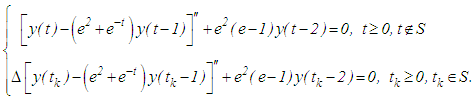
- We observe that all conditions of Theorem 3.2, except for
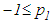 are satisfied. Note that
are satisfied. Note that 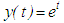 is a non-oscillating solution of this equation.
is a non-oscillating solution of this equation.4. Conclusions
- By appropriate imposition of impulse controls, all solutions of a certain class of second order neutral impulsive differential equations are observed to be oscillatory. In this paper, we generalized and proved the results of oscillations of second order neutral differential equations with constant coefficients obtained by Bainov and Mishev [3] for impulsive differential equations.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML