Uchenna Okwudili Anekwe, Emmanuel Hassan
Department of Physics, University of Science and Technology, Aleiro, Nigeria
Correspondence to: Uchenna Okwudili Anekwe, Department of Physics, University of Science and Technology, Aleiro, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Special form of integration involves method of integrating the product of a dependable variable (x) of a certain degree from Negative infinity to positive infinity together with an exponential function of that dependent variable(x) to the second degree. Integral function with the power of the dependent variable(x) multiplying that of the exponential function of that dependent variable(x) to the second power having an odd powers i.e ranging from x=1,2,3,5…. or an even powers i.e ranging from x=0,2,4,6… Have a general formular called the Anekwe’s integral Formular. The Anekwe’s integral Formular is a formular discovered to solve the product of the exponential function of the second power of the dependent variable together with the dependent variable (x) ranging from Negative infinity to positive infinity in order to solve functions of this nature with ease rather than using the gamma function. In this Manuscript the Special form of integration derived, is Applied in solving problems in statistical and Thermal Physics in terms of Speed and Energy of a given particle in motion.
Keywords:
Integration by part, Trigonometry, Velocity, Energy
Cite this paper: Uchenna Okwudili Anekwe, Emmanuel Hassan, Application of the Special form of Integration to Statistical and Thermal Physics, Applied Mathematics, Vol. 7 No. 2, 2017, pp. 32-37. doi: 10.5923/j.am.20170702.03.
1. Introduction
The motive behind this research article is to derive a formula that can be able to solve integral fuctions involving exponential functions of x to the second power in connection to the product of its dependable variable x of a certain degree, and to compare its result obtained with results obtained when solved using gamma function. Example, like in the case of finding the gamma function of half (1/2) which is equal to the square-root of pie, also to solve other complex integrals of the famous bell shaped curve of probability theory, and later applying the same integrals derived in solving problems in statistical and thermal physics in terms of the speed and energy of a given particle in motion.The Gamma function is defined by an improper integral function which provides a way of giving a meaning to the “factorial” of any positive real number. Another reason for interest in the gamma function is its relation to integrals that arise in the study of probability. The graph of the function ϕ defined by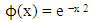 is the famous “bell-shaped curve” of probability theory. It can be shown that the anti-derivatives of ϕ are not expressible in terms of elementary functions. On the other hand,
is the famous “bell-shaped curve” of probability theory. It can be shown that the anti-derivatives of ϕ are not expressible in terms of elementary functions. On the other hand,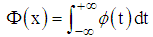 is, by the fundamental theorem of calculus, an anti-derivative of ϕ, and information about its values is useful.
is, by the fundamental theorem of calculus, an anti-derivative of ϕ, and information about its values is useful.
2. Methodology
In this section we shall consider how to of integrate the product of a dependable variable (x) of a certain degree from Negative infinity to positive infinity together with an exponential function of that dependent variable(x) to the second degree and apply the results obtained from these integrals in solving problems relating to speed and energy of a particle in motion in statistical and thermal physics.Example 2.1 CASE 1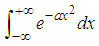 SOLUTIONFig. (a)
SOLUTIONFig. (a)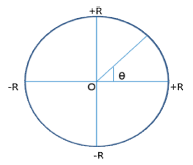 Let
Let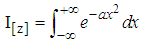 | (1) |
Since from fig. (a) we’ve both the combination of real and imaginary axis 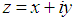 is a combination of both real and imaginary
is a combination of both real and imaginary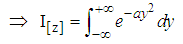 | (2) |
Multiplying eqn (1) by (2) we’ve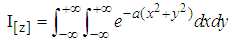 | (3) |
But 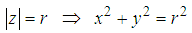 | (4) |
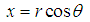 | (5) |
And 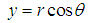 | (6) |
But 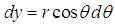 , where
, where 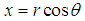
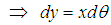 | (7) |
Also from 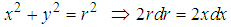
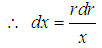 | (8) |
Substituting eqn (4), (5), (6), (7) & (8) into eqn (3) we’ve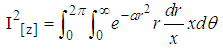 | (9) |
Note that the limit was taking from zero to 2π simply because in fig. (a) we’ve four quadrant of which from eqn (9) No quadrant is specified i.e either sinθ, cosθ, tanθ, why that of r ranges from 0 to R(∞) 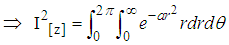 | (10) |
From eqn (10) we’ve 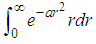 where we’ve
where we’ve 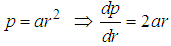
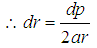
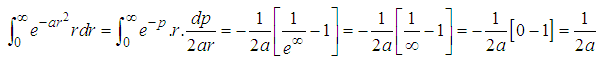 | (11) |
Putting eqn (11) back into eqn (10) we’ve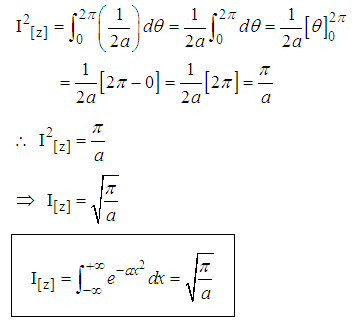 Example 2.2 CASE 2
Example 2.2 CASE 2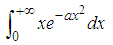 SOLUTION
SOLUTION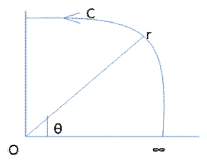 Given that we’ve
Given that we’ve 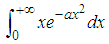
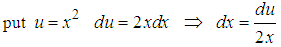
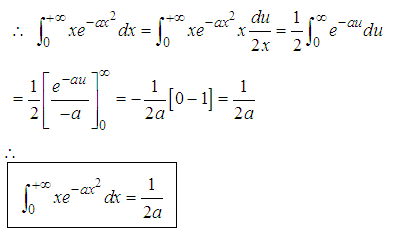 From the results obtained above we’ve the general formula for the set of all odd integer powers of x as
From the results obtained above we’ve the general formula for the set of all odd integer powers of x as 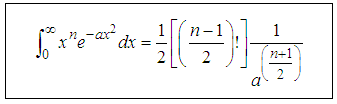 i.e for n=1,3,5,7…… all set odd numbersAlso from the results obtained above we’ve the General formular for the set of all even integer powers of x as
i.e for n=1,3,5,7…… all set odd numbersAlso from the results obtained above we’ve the General formular for the set of all even integer powers of x as From the General formular for the set of all even integer powers of x we’ve
From the General formular for the set of all even integer powers of x we’ve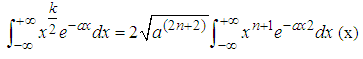 Where
Where 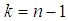 Equation (x) is the Anekwe’s integral formula for solving integration of exponential functions to the first degree.The three general formula stated above are known as the Anekwe’s integral Formular.Using the Anekwe’s integral formula generated above we’ve
Equation (x) is the Anekwe’s integral formula for solving integration of exponential functions to the first degree.The three general formula stated above are known as the Anekwe’s integral Formular.Using the Anekwe’s integral formula generated above we’ve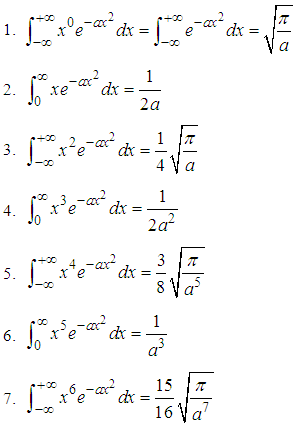 Application To Statistical And Thermal PhysicsApplication of the Special form of integration in Statistical and Thermal Physics which we shall look on, has to do with the Application of the Results obtained from Special Form of integration in deriving the equations of the Speed and Energy of a particle in motion in terms of Statistical and Thermal Physics.The Special Form of integration Seen above has a Significant Application in determining, The most probable velocity of the particle at a temperature T, Root-mean-square speed of the particle, The Most Probable Kinetic energy of a gas molecule at a temperature T, The mean Kinetic energy of a gas molecule at a temperature T, and The root-mean Square Kinetic energy of a gas molecule at a temperature T, in Statistical and Thermal physics which we Shall discuss in this section through worked examples.Example 2.3Using the equation of the number of particles obtained from the Maxwell’s velocity distribution Curve, Show that the most probable velocity of a gas molecule is
Application To Statistical And Thermal PhysicsApplication of the Special form of integration in Statistical and Thermal Physics which we shall look on, has to do with the Application of the Results obtained from Special Form of integration in deriving the equations of the Speed and Energy of a particle in motion in terms of Statistical and Thermal Physics.The Special Form of integration Seen above has a Significant Application in determining, The most probable velocity of the particle at a temperature T, Root-mean-square speed of the particle, The Most Probable Kinetic energy of a gas molecule at a temperature T, The mean Kinetic energy of a gas molecule at a temperature T, and The root-mean Square Kinetic energy of a gas molecule at a temperature T, in Statistical and Thermal physics which we Shall discuss in this section through worked examples.Example 2.3Using the equation of the number of particles obtained from the Maxwell’s velocity distribution Curve, Show that the most probable velocity of a gas molecule is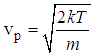 Where
Where  has a maximum and represents the number of particles having momentum from p to p+dp.SolutionGiven that we’ve
has a maximum and represents the number of particles having momentum from p to p+dp.SolutionGiven that we’ve 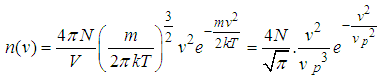 | (1) |
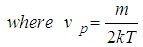 | (2) |
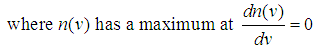 | (3) |
Differentiating both sides of equation (3) w.r.t v and setting its derivative to be equal to zero we’ve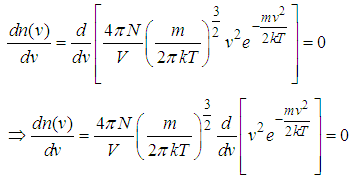 | (4) |
Using product rule of differentiation we’ve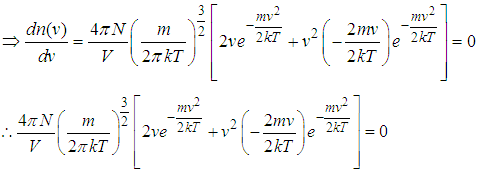 On factorization we’ve
On factorization we’ve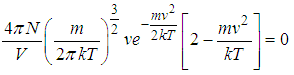 | (5) |
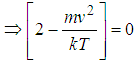 | (6) |
Making V the subject of formula we’ve the most probable velocity to be given by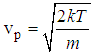 Example 2.4Given that the number of particles having momentum p to
Example 2.4Given that the number of particles having momentum p to 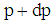 in terms of most probable velocity is given by
in terms of most probable velocity is given by 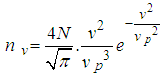 show that the root-mean square speed
show that the root-mean square speed 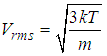 SOLUTIONThe expression for the root mean square velocity is
SOLUTIONThe expression for the root mean square velocity is 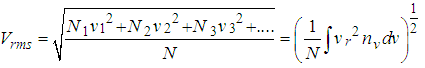 | (1) |
Given that 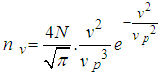 | (2) |
 substituting eqn(1) into eqn (2) we’ve
substituting eqn(1) into eqn (2) we’ve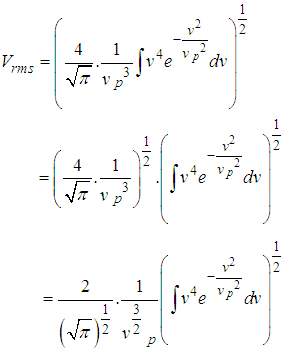 | (3) |
From case (5) we’ve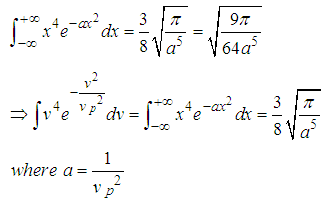 On substitution into eqn (3) we’ve
On substitution into eqn (3) we’ve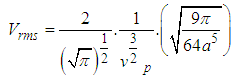 | (4) |
Where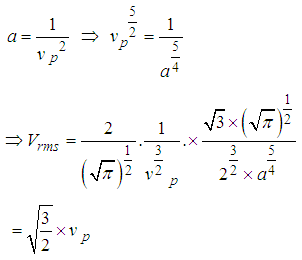 | (5) |
Given that the most probable velocity 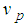 is given by
is given by 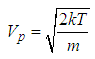 | (6) |
Substituting eqn(6)into eqn(5) we’ve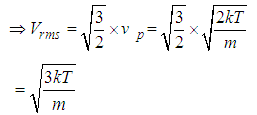 | (7) |
Example 2.5Use the Maxwell’s Energy distribution function given by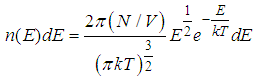 to obtaina. The Most Probable Kinetic energy of a gas molecule at a temperature Tb. The mean Kinetic energy of a gas molecule at a temperature at T, and c. The root-mean-Square Kinetic energy of a gas molecule at a temperature at T.Solutiona). Given that
to obtaina. The Most Probable Kinetic energy of a gas molecule at a temperature Tb. The mean Kinetic energy of a gas molecule at a temperature at T, and c. The root-mean-Square Kinetic energy of a gas molecule at a temperature at T.Solutiona). Given that 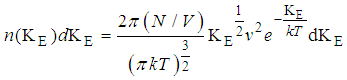 | (1) |
Where KE represents the kinetic energy of the given gas molecule (E= KE).The most probable value of the kinetic energy occurs when 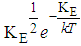 has a minimum i.e (d/d KE)=0. Using product rule of differentiation we’ve
has a minimum i.e (d/d KE)=0. Using product rule of differentiation we’ve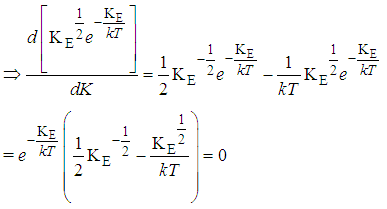 | (2) |
 | (3) |
Making KE the subject of formula we’ve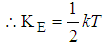 | (4) |
b) Given that 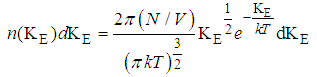 | (5) |
Where KE represents the kinetic energy of the given gas molecule (E= KE) The mean Kinetic energy of a gas molecule at a temperature T is given by 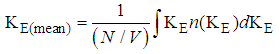 | (6) |
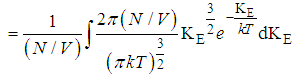 | (7) |
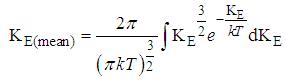 | (8) |
From Equation (x) above using Anekwe’s integral formula for solving integration of exponential functions to the first degree we’ve.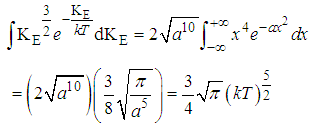 | (9) |
Where a = kTSubstituting equation (9) back into equation (8) we’ve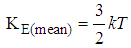 | (10) |
c) Given that 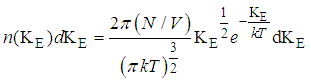 Where KE represents the kinetic energy of the given gas molecule (E= KE) The root-mean-Square Kinetic energy of a gas molecule at a temperature at T is given by
Where KE represents the kinetic energy of the given gas molecule (E= KE) The root-mean-Square Kinetic energy of a gas molecule at a temperature at T is given by 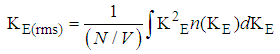 | (11) |
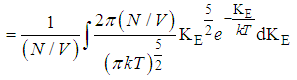 | (12) |
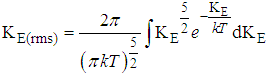 | (13) |
From Equation (x) above using Anekwe’s integral formula for solving integration of exponential functions to the first degree.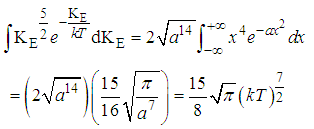 | (14) |
Where a = kTSubstituting equation (14) back into equation (13) we’ve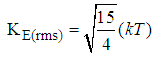 | (15) |
Example 2.6Consider the motion of a particle in a given gas molecules of mass 2.0kg at a temperature of 100kDeterminea. The most probable velocity of the particleb. Root-mean-square speed of the particlec. Most probable Kinetic Energy of the particled. Mean Kinetic Energy of the particle ande. Root-mean-square Kinetic Energy of the particle.[Take k(boltzman constant)=1.38x10-23JK-1 ]Solution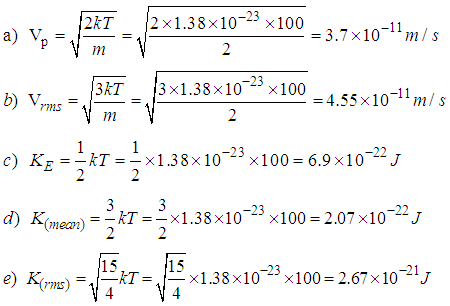 Example 2.7Consider a particle in an infinite potential well of mass m=3k (boltzman constant) at a temperature of 110KDeterminea). The Root-mean-square speed of the particle and b). The root-mean-square Kinetic energy of the particle in an infinite well.Solution
Example 2.7Consider a particle in an infinite potential well of mass m=3k (boltzman constant) at a temperature of 110KDeterminea). The Root-mean-square speed of the particle and b). The root-mean-square Kinetic energy of the particle in an infinite well.Solution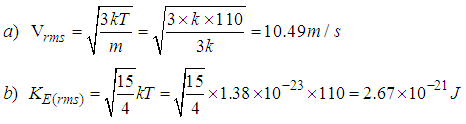
3. Conclusions
From the calculations done above it can be seen that the Anekwe’s integral formular is an easy and fast way of solving integral involving the product of the dependent variable raging from zero to infinity i.e x=0,1,2,3…together with an exponential fuction of the second degree of that dependent variable and when compared the answers to that of gamma fuction it would be seen that both method gives the same answer of which Anekwe’s integral formular is faster and reliable for higher powers of the dependent variable pre-multiplying that of the exponential function. Lastly, from the calculation done above we’ve seen that the results obtained using the Anekwe’s integral formula has an Application in determining the speed and Energy of a giving particle in motion in terms of Statistical and Thermal Physics.
ACKNOWLEDGEMENTS
Our sincere acknowledge goes to the presence of the Almighty God, the source of wisdom and inspiration for giving us the wisdom to complete this research article and to use this medium to Acknowledge all our reviewers and to say a big thank you for all of your contributions to the success of this research work.
References
| [1] | R. Courant, Differential and Integral Calculus (2 volumes), English translation by E. J. McShane, Interscience Publishers, New York, 1961. |
| [2] | E. T. Whittaker & G. N. Watson, A Course of Modern Analysis, 4th edition, Cambridge University Press, 1969. |
| [3] | David Widder, Advanced Calculus, 2nd edition, Prentice Hall, 1961. |
| [4] | Ahmed H. Hussein, Statistical Physics, Home WorkSolutions. chp 9, Modern Physics II Winter 2004. |


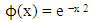 is the famous “bell-shaped curve” of probability theory. It can be shown that the anti-derivatives of ϕ are not expressible in terms of elementary functions. On the other hand,
is the famous “bell-shaped curve” of probability theory. It can be shown that the anti-derivatives of ϕ are not expressible in terms of elementary functions. On the other hand,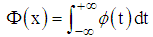 is, by the fundamental theorem of calculus, an anti-derivative of ϕ, and information about its values is useful.
is, by the fundamental theorem of calculus, an anti-derivative of ϕ, and information about its values is useful.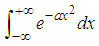 SOLUTIONFig. (a)
SOLUTIONFig. (a) Let
Let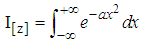
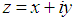 is a combination of both real and imaginary
is a combination of both real and imaginary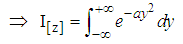
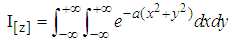
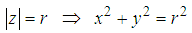
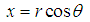
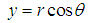
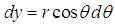 , where
, where 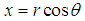
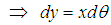
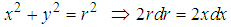
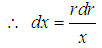
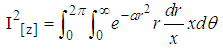
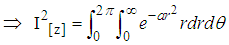
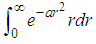 where we’ve
where we’ve 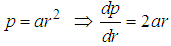
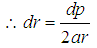
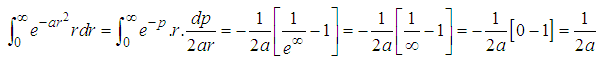
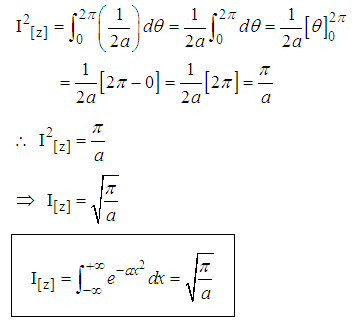 Example 2.2 CASE 2
Example 2.2 CASE 2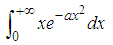 SOLUTION
SOLUTION Given that we’ve
Given that we’ve 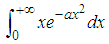
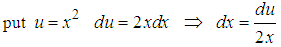
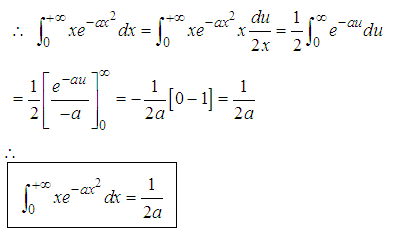 From the results obtained above we’ve the general formula for the set of all odd integer powers of x as
From the results obtained above we’ve the general formula for the set of all odd integer powers of x as 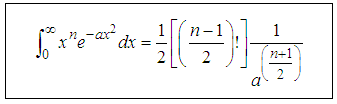 i.e for n=1,3,5,7…… all set odd numbersAlso from the results obtained above we’ve the General formular for the set of all even integer powers of x as
i.e for n=1,3,5,7…… all set odd numbersAlso from the results obtained above we’ve the General formular for the set of all even integer powers of x as From the General formular for the set of all even integer powers of x we’ve
From the General formular for the set of all even integer powers of x we’ve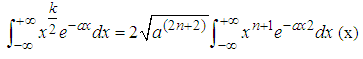 Where
Where 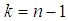 Equation (x) is the Anekwe’s integral formula for solving integration of exponential functions to the first degree.The three general formula stated above are known as the Anekwe’s integral Formular.Using the Anekwe’s integral formula generated above we’ve
Equation (x) is the Anekwe’s integral formula for solving integration of exponential functions to the first degree.The three general formula stated above are known as the Anekwe’s integral Formular.Using the Anekwe’s integral formula generated above we’ve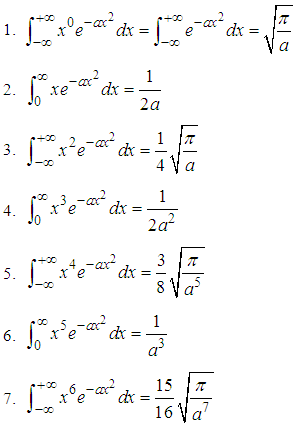 Application To Statistical And Thermal PhysicsApplication of the Special form of integration in Statistical and Thermal Physics which we shall look on, has to do with the Application of the Results obtained from Special Form of integration in deriving the equations of the Speed and Energy of a particle in motion in terms of Statistical and Thermal Physics.The Special Form of integration Seen above has a Significant Application in determining, The most probable velocity of the particle at a temperature T, Root-mean-square speed of the particle, The Most Probable Kinetic energy of a gas molecule at a temperature T, The mean Kinetic energy of a gas molecule at a temperature T, and The root-mean Square Kinetic energy of a gas molecule at a temperature T, in Statistical and Thermal physics which we Shall discuss in this section through worked examples.Example 2.3Using the equation of the number of particles obtained from the Maxwell’s velocity distribution Curve, Show that the most probable velocity of a gas molecule is
Application To Statistical And Thermal PhysicsApplication of the Special form of integration in Statistical and Thermal Physics which we shall look on, has to do with the Application of the Results obtained from Special Form of integration in deriving the equations of the Speed and Energy of a particle in motion in terms of Statistical and Thermal Physics.The Special Form of integration Seen above has a Significant Application in determining, The most probable velocity of the particle at a temperature T, Root-mean-square speed of the particle, The Most Probable Kinetic energy of a gas molecule at a temperature T, The mean Kinetic energy of a gas molecule at a temperature T, and The root-mean Square Kinetic energy of a gas molecule at a temperature T, in Statistical and Thermal physics which we Shall discuss in this section through worked examples.Example 2.3Using the equation of the number of particles obtained from the Maxwell’s velocity distribution Curve, Show that the most probable velocity of a gas molecule is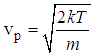 Where
Where  has a maximum and represents the number of particles having momentum from p to p+dp.SolutionGiven that we’ve
has a maximum and represents the number of particles having momentum from p to p+dp.SolutionGiven that we’ve 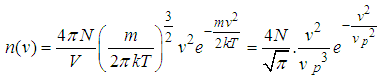
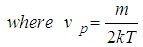
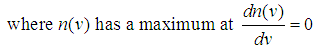
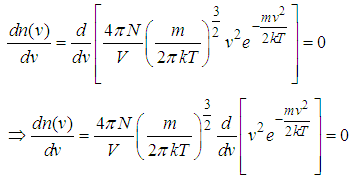
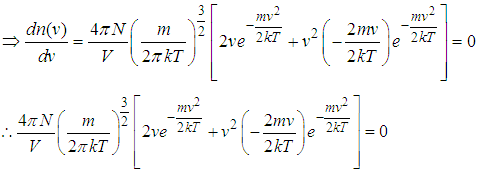 On factorization we’ve
On factorization we’ve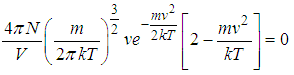
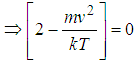
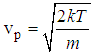 Example 2.4Given that the number of particles having momentum p to
Example 2.4Given that the number of particles having momentum p to 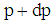 in terms of most probable velocity is given by
in terms of most probable velocity is given by 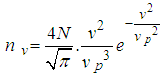 show that the root-mean square speed
show that the root-mean square speed 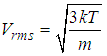 SOLUTIONThe expression for the root mean square velocity is
SOLUTIONThe expression for the root mean square velocity is 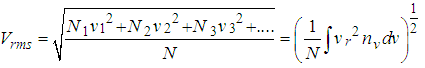
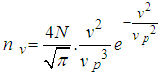
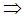 substituting eqn(1) into eqn (2) we’ve
substituting eqn(1) into eqn (2) we’ve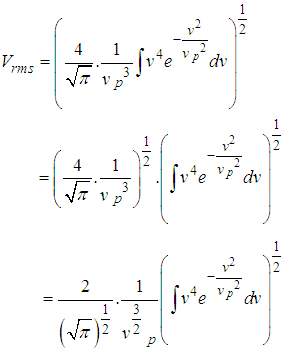
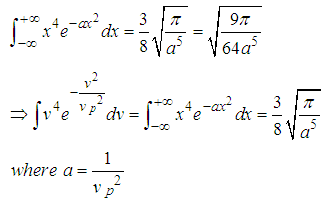 On substitution into eqn (3) we’ve
On substitution into eqn (3) we’ve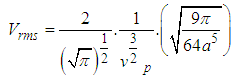
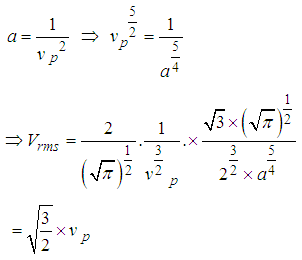
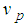 is given by
is given by 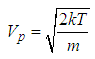
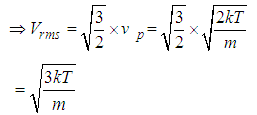
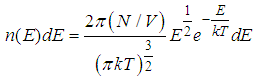 to obtaina. The Most Probable Kinetic energy of a gas molecule at a temperature Tb. The mean Kinetic energy of a gas molecule at a temperature at T, and c. The root-mean-Square Kinetic energy of a gas molecule at a temperature at T.Solutiona). Given that
to obtaina. The Most Probable Kinetic energy of a gas molecule at a temperature Tb. The mean Kinetic energy of a gas molecule at a temperature at T, and c. The root-mean-Square Kinetic energy of a gas molecule at a temperature at T.Solutiona). Given that 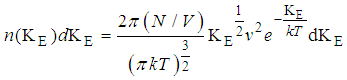
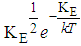 has a minimum i.e (d/d KE)=0. Using product rule of differentiation we’ve
has a minimum i.e (d/d KE)=0. Using product rule of differentiation we’ve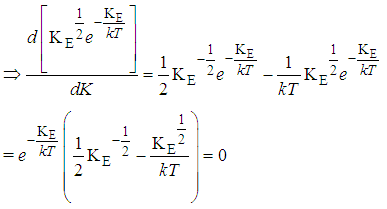

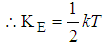
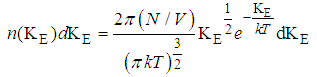
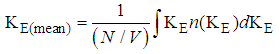
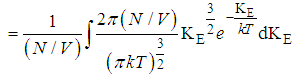
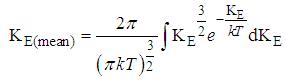
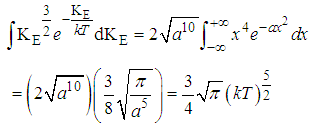
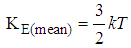
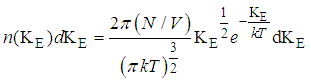 Where KE represents the kinetic energy of the given gas molecule (E= KE) The root-mean-Square Kinetic energy of a gas molecule at a temperature at T is given by
Where KE represents the kinetic energy of the given gas molecule (E= KE) The root-mean-Square Kinetic energy of a gas molecule at a temperature at T is given by 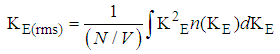
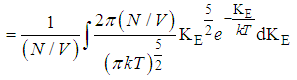
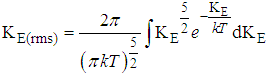
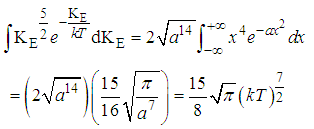
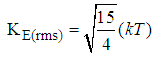
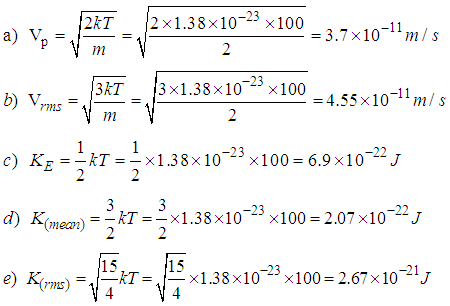 Example 2.7Consider a particle in an infinite potential well of mass m=3k (boltzman constant) at a temperature of 110KDeterminea). The Root-mean-square speed of the particle and b). The root-mean-square Kinetic energy of the particle in an infinite well.Solution
Example 2.7Consider a particle in an infinite potential well of mass m=3k (boltzman constant) at a temperature of 110KDeterminea). The Root-mean-square speed of the particle and b). The root-mean-square Kinetic energy of the particle in an infinite well.Solution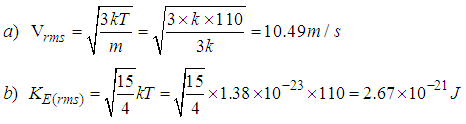
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML