-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2017; 7(1): 14-17
doi:10.5923/j.am.20170701.03

The Restrained Monophonic Domination Number of Graph
P. Arul Paul Sudhahar1, C. Bency2, A. Vijayan
1Department of Mathematics, Rani Anna Government College for Women Thirunelveli, India
2Department of Mathematics, Nesamony Memorial Christian College Marthandam, India
Correspondence to: P. Arul Paul Sudhahar, Department of Mathematics, Rani Anna Government College for Women Thirunelveli, India.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A set M of vertices of a connected graph G is a monophonic set if every vertex of G lies on a x - y monophonic path for some elements x and y in M. The minimum cardinality of a monophonic set of G is the monophonic number of G, denoted by m(G). A set M of vertices of a connected graph G is a monophonic dominating set if M is both a monophonic set and a dominating set. The minimum cardinality of a monophonic dominating set of G is the monophonic domination number of G, denoted by 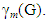 A set M of vertices of a connected graph G is a restrained monophonic dominating set if either V = M or M is a monophonic dominating set with the subgraph G[V – M] induced by V – M has no isolated vertices. The minimum cardinality of a restrained monophonic dominating set of G is the restrained monophonic domination number of G and is denoted by mr(G). The restrained monophonic domination number of some connected graph are realized. It is shown that, for any positive integers a, b and c with 3 ≤ a ≤ b < c, there exists a connected graph G such that m(G) = a,
A set M of vertices of a connected graph G is a restrained monophonic dominating set if either V = M or M is a monophonic dominating set with the subgraph G[V – M] induced by V – M has no isolated vertices. The minimum cardinality of a restrained monophonic dominating set of G is the restrained monophonic domination number of G and is denoted by mr(G). The restrained monophonic domination number of some connected graph are realized. It is shown that, for any positive integers a, b and c with 3 ≤ a ≤ b < c, there exists a connected graph G such that m(G) = a,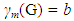 and
and 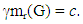
Keywords: Monophonic set, Monophonic number, Monophonic dominating set, Monophonic domination number, Restrained monophonic dominating set, Restrained monophonic domination number
Cite this paper: P. Arul Paul Sudhahar, C. Bency, A. Vijayan, The Restrained Monophonic Domination Number of Graph, Applied Mathematics, Vol. 7 No. 1, 2017, pp. 14-17. doi: 10.5923/j.am.20170701.03.
Article Outline
1. Introduction
- By a graph G = (V, E), we mean a finite undirected connected graph without loops or multiple edges. The order and size of G are denoted by p and q respectively. For basic graph theoretic terminology we refer to [2, 4, 5]. The neighborhood of a vertex v is the set N(v) consisting of all vertices u which are adjacent with v. The closed neighborhood of a vertex v is the set N[v] = N(v) ⋃{v}. A vertex v is an extreme vertex if the subgraph induced by its neighbors is complete. A vertex v is a semi-extreme vertex of G if the subgraph induced by its neighbors has a full degree vertex in N(v). In particular, every extreme vertex is a semi-extreme vertex and a semi-extreme vertex need not be an extreme vertex.A chord of a path u1, u2,…,uk in G is an edge uiuj with j ≥ i + 2. A u – v path P is called a monophonic path if it is a chordless path. A set M of vertices is a monophonic set if every vertex of G lies on a monophonic path joining some pair of vertices in M, and the minimum cardinality of a monophonic set is the monophonic number m(G). A monophonic set of cardinality m(G) is called an m-set of G. The monophonic number of a graph G was studied in [3]. A dominating set in a graph G is a subset of vertices of G such that every vertex outside the subset has a neighbor in it. The size of a minimum dominating set in a graph G is called the domination number of G and is denoted
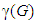 [6]. A set of vertices of G is said to be monophonic domination set if it is both monophonic set and a dominating set of G. The minimum cardinality among all the monophonic dominating sets of G is called a monophonic domination number and is denoted by
[6]. A set of vertices of G is said to be monophonic domination set if it is both monophonic set and a dominating set of G. The minimum cardinality among all the monophonic dominating sets of G is called a monophonic domination number and is denoted by 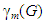 [8]. The restrained edge monophonic number of a graph was studied in [9].Theorem 1.1 [10] Each extreme vertex of a connected graph G belongs to every monophonic set of G.Throughout this paper G denotes a connected graph with at least two vertices.
[8]. The restrained edge monophonic number of a graph was studied in [9].Theorem 1.1 [10] Each extreme vertex of a connected graph G belongs to every monophonic set of G.Throughout this paper G denotes a connected graph with at least two vertices.2. Restrained Monophonic Domination Number
- Definition 2.1 A set M of vertices of a connected graph G is a restrained monophonic domination set if either V= M or M is a monophonic dominating set with the subgraph G[V – M] induced by V – M has no isolated vertices. The minimum cardinality of a restrained monophonic dominating set of G is the restrained monophonic domination number of G, and is denoted by
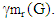 Example 2.2 For the graph G given in Figure 1, M 1 = {v1 , v4 } is a monophonic set of G and so m(G) = 2; M2 = {v1 , v4 , v10} is a monophonic dominating set of G and so
Example 2.2 For the graph G given in Figure 1, M 1 = {v1 , v4 } is a monophonic set of G and so m(G) = 2; M2 = {v1 , v4 , v10} is a monophonic dominating set of G and so 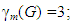 M3 = {v1 , v4 ,v10,v11} is a restrained monophonic dominating set of G and so
M3 = {v1 , v4 ,v10,v11} is a restrained monophonic dominating set of G and so 
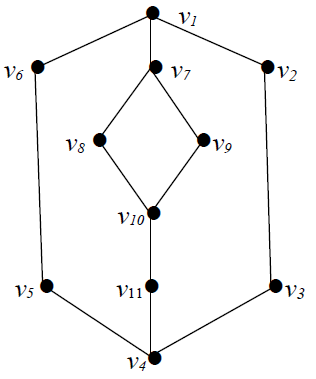 | Figure 1. A graph G for restrained monophonic domination numbers |
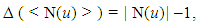 there exists v ∈ N(u) such that
there exists v ∈ N(u) such that 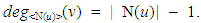 Since N is a restrained monophonic dominating set of G, the edge e = u v lies on a x - y monophonic path P : x = x0, x1,….,xi-1, xi = u, xi+1 = v,…,x n = y with x, y ∈ N. Since u ∉ N, it is clear that u is an internal vertex of a path P. Since
Since N is a restrained monophonic dominating set of G, the edge e = u v lies on a x - y monophonic path P : x = x0, x1,….,xi-1, xi = u, xi+1 = v,…,x n = y with x, y ∈ N. Since u ∉ N, it is clear that u is an internal vertex of a path P. Since 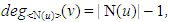 we see that v is adjacent to xi-1, which is a contradiction to the fact that P is a x – y monophonic path. Hence M is contained in every restrained monophonic dominating set of G.Theorem 2.4 For any connected graph G,
we see that v is adjacent to xi-1, which is a contradiction to the fact that P is a x – y monophonic path. Hence M is contained in every restrained monophonic dominating set of G.Theorem 2.4 For any connected graph G, 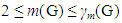
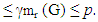 Proof. A monophonic set needs at least two vertices and therefore m(G) ≥ 2. Also every monophonic dominating set is a monophonic set of G, and then
Proof. A monophonic set needs at least two vertices and therefore m(G) ≥ 2. Also every monophonic dominating set is a monophonic set of G, and then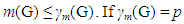 or p – 1, then mr(G) = p the converse need not be true. Also since every restrained monophonic dominating set of G is an monophonic dominating set of G, and then
or p – 1, then mr(G) = p the converse need not be true. Also since every restrained monophonic dominating set of G is an monophonic dominating set of G, and then 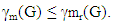 The complement of each restrained monophonic dominating set has cardinality different from 1 we have
The complement of each restrained monophonic dominating set has cardinality different from 1 we have 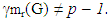 Thus there is no graph G of order p with
Thus there is no graph G of order p with 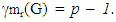 Hence
Hence 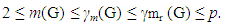 Theorem 2.5 If a graph G of order p has exactly one vertex of degree p – 1, then
Theorem 2.5 If a graph G of order p has exactly one vertex of degree p – 1, then 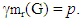 Proof. Let G be a Graph of order p with exactly one vertex of degree p – 1, and let it be u. Since the vertex u is adjacent to all other vertices in G, then any vertex v where v ∈V(G) - {u}, is not an internal vertex of any monophonic path joining two vertices of G other than u and v. Hence
Proof. Let G be a Graph of order p with exactly one vertex of degree p – 1, and let it be u. Since the vertex u is adjacent to all other vertices in G, then any vertex v where v ∈V(G) - {u}, is not an internal vertex of any monophonic path joining two vertices of G other than u and v. Hence 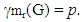 Corollary 2.6 For the complete graph Kp( p ≥ 2),
Corollary 2.6 For the complete graph Kp( p ≥ 2), 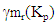
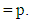 Proof. Since every vertex of the complete graph Kp (p ≥ 2) is a extreme vertex, by Theorem 2.3, the vertex set of Kp is the minimum restrained monophonic dominating set of Kp. Thus
Proof. Since every vertex of the complete graph Kp (p ≥ 2) is a extreme vertex, by Theorem 2.3, the vertex set of Kp is the minimum restrained monophonic dominating set of Kp. Thus 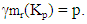 Theorem 2.7 For the complete bipartite graph G = Km,n ,
Theorem 2.7 For the complete bipartite graph G = Km,n , 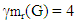 if 3 ≤ m ≤ n.Proof. Let X and Y be the partite sets with |X| = m, |Y| = n. If 3 ≤ m ≤ n, then any minimum restrained monophonic dominating set of G is got by choosing two elements from X and Y so that
if 3 ≤ m ≤ n.Proof. Let X and Y be the partite sets with |X| = m, |Y| = n. If 3 ≤ m ≤ n, then any minimum restrained monophonic dominating set of G is got by choosing two elements from X and Y so that 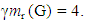
3. Realization Result
- Theorem 3.1 For any integers a, b, c with 3 ≤ a ≤ b < c, then there exists a connected graph G such that m(G) = a,
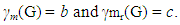 Proof. Case 1 3 ≤ a = b < c Let P : x, y, z be a path of order 3. We first add a – 1 new vertices u1, u2,....,ua-1 to P and join these to x. We then add c – a new vertices w1,w2,…,wc-a and join these to both x and z, there by producing the graph G given in Figure 2.
Proof. Case 1 3 ≤ a = b < c Let P : x, y, z be a path of order 3. We first add a – 1 new vertices u1, u2,....,ua-1 to P and join these to x. We then add c – a new vertices w1,w2,…,wc-a and join these to both x and z, there by producing the graph G given in Figure 2.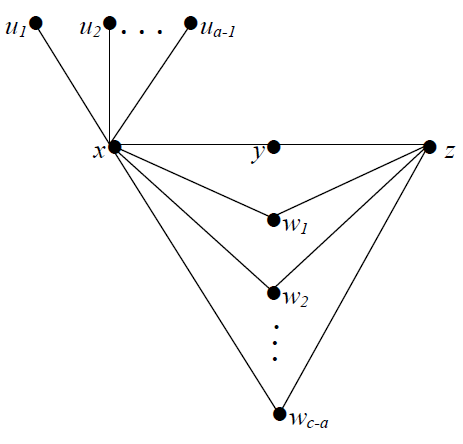 | Figure 2. The graph G in Case 1 of Theorem 3.1 |
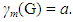 Next, we show that
Next, we show that 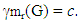 M2 = M ⋃{w1, w2, …, wc-a} is a minimum restrained monophonic dominating set of G, so that
M2 = M ⋃{w1, w2, …, wc-a} is a minimum restrained monophonic dominating set of G, so that 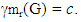 Case 2 a + 1 = b < cLet C6 : v1, v2, v3, v4, v5, v6 be a cycle of order 6, and let P3: x, y ,z be a path of order 3. Let H be a graph obtained from C6 and P3 by identifying the vertex v1 in C6 and the vertex z in P3. We first add a – 1 new vertices u1, u2,...,ua-1 to H, and join these to x. We then add c – b new vertices w1,w2,...., wc-b and join these to both v2 and v4, there by producing the graph G given in Figure 3.
Case 2 a + 1 = b < cLet C6 : v1, v2, v3, v4, v5, v6 be a cycle of order 6, and let P3: x, y ,z be a path of order 3. Let H be a graph obtained from C6 and P3 by identifying the vertex v1 in C6 and the vertex z in P3. We first add a – 1 new vertices u1, u2,...,ua-1 to H, and join these to x. We then add c – b new vertices w1,w2,...., wc-b and join these to both v2 and v4, there by producing the graph G given in Figure 3.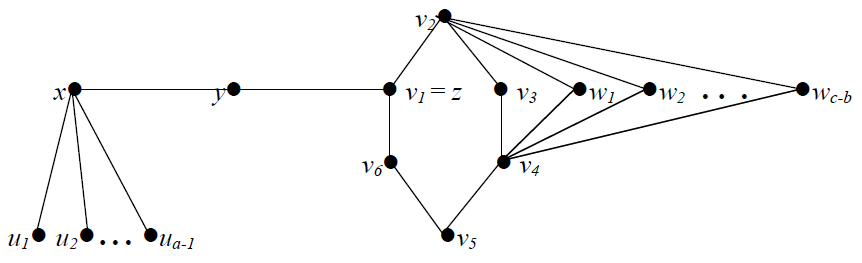 | Figure 3. The graph G in Case 2 of Theorem 3.1 |
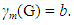 Let M2 = M1 ⋃ {v1} is a monophonic dominating set of G, and so
Let M2 = M1 ⋃ {v1} is a monophonic dominating set of G, and so 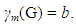 It is clear that M3 = M ⋃ { w1, w2,....,wc-b} is a minimum restrained monophonic dominating set of G, so that
It is clear that M3 = M ⋃ { w1, w2,....,wc-b} is a minimum restrained monophonic dominating set of G, so that 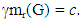 Case 3 a + 2 ≤ b < cLet C4 :v1, v2, v3, v4 be a cycle of order 4, and let P : u1,u2,....,u3(b-a) be a path of order 3(b – a). Let H be a graph obtained from C4 and P by identifying the vertex v4 in C4 and u1 in P, and then joining v4 and u1. We first add a – 1 new vertices z1, z2,....za-1 to H and join these to v1. We then add c – b new vertices w1,w2,....,wc-b and join these to both v1 and v4, there by producing the graph G given in Figure 4.
Case 3 a + 2 ≤ b < cLet C4 :v1, v2, v3, v4 be a cycle of order 4, and let P : u1,u2,....,u3(b-a) be a path of order 3(b – a). Let H be a graph obtained from C4 and P by identifying the vertex v4 in C4 and u1 in P, and then joining v4 and u1. We first add a – 1 new vertices z1, z2,....za-1 to H and join these to v1. We then add c – b new vertices w1,w2,....,wc-b and join these to both v1 and v4, there by producing the graph G given in Figure 4.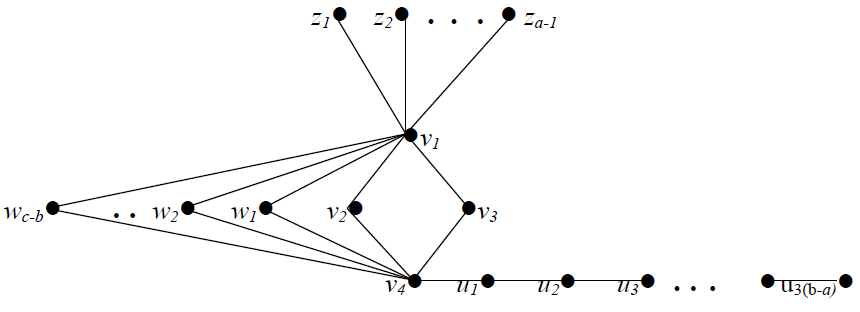 | Figure 4. The graph G in Case 3 of Theorem 3.1 |
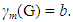 It is clear that M1 is not a monophonic dominating set of G. Clearly M2 = M1 ⋃ { v4, u2, u5, ...., u3(b-a)} is a monophonic dominating set of G, and so
It is clear that M1 is not a monophonic dominating set of G. Clearly M2 = M1 ⋃ { v4, u2, u5, ...., u3(b-a)} is a monophonic dominating set of G, and so 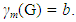 Next, we show that
Next, we show that 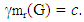 It is clear that M3 = M2 ⋃ {w1,w2,....,wc-b} is a minimum restrained monophonic dominating set of G, and so that
It is clear that M3 = M2 ⋃ {w1,w2,....,wc-b} is a minimum restrained monophonic dominating set of G, and so that 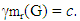
4. Conclusions
- In this paper the authors introduced the restrained monophonic domination number and the restrained monophonic domination number of some connected graph are realized. The authors obtained the restrained edge monophonic domination number, connected restrained monophonic domination number, and forcing restrained monophonic domination number in the subsequent papers. It has so many application in security of buildings and communication networks.
ACKNOWLEDGEMENTS
- The authors are grateful to the anonymous referee for a careful checking of the details and for helpful comments that improved this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML