Nejmaddin A. Sulaiman1, Rebaz B. Mustafa2
1Department of Mathematics, College of Education, Salahaddin University, Erbil, Iraq
2Business Management Department, Technical College, Erbil Polytechnic University, Iraq
Correspondence to: Rebaz B. Mustafa, Business Management Department, Technical College, Erbil Polytechnic University, Iraq.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper we presented a class of optimization problems known as extreme point multi-objective linear programming problem. We propose a new technique (Harmonic Mean) to transform an extreme point multi-objective linear programming problem (EPMOLPP) to an extreme point single objective linear programming problem (EPSOLPP). We provide an algorithm for our methodology, to solve such a class of problems. Two numerical examples are given to elucidate our proposed algorithm.
Keywords:
EPMOLPP, Harmonic Mean
Cite this paper: Nejmaddin A. Sulaiman, Rebaz B. Mustafa, Transform Extreme Point Multi-Objective Linear Programming Problem to Extreme Point Single Objective Linear Programming Problem by Using Harmonic Mean, Applied Mathematics, Vol. 6 No. 5, 2016, pp. 95-99. doi: 10.5923/j.am.20160605.01.
1. Introduction
An extreme point mathematical programming is a class of optimization problems in which the objective function has to be optimized over a convex region with the additional requirement that the optimal value should exist on an extreme point of another convex region. Plenty of works have been done in extreme point linear programming problem [2, 5]. Below indicate some researchers work in this field which were investigated by Swarup, et al. in (1972) and Kanti Swarup; Gupta in (1973, 1978). Sulaiman [9] developed the computational aspects of single-objective indefinite quadratic programming problem with extreme point, in which the product of two linear functions is optimized subject to constraints of linear inequalities with the additional restriction that the optimum solution should be an extreme point of another convex polyhedron formed by another set of linear constraints. Hamad-Amin [4] used average technique to solve an extreme point complementary multi-objective linear programming problem (EPCMOLPP). Salih [8] proposed extreme point linear fractional programming problem. Abdulrahim [1] studied on extreme point quadratic fractional programming problem. Sulaiman et al [10] presented optimal geometric average technique to solve an extreme point multi- objective quadratic programming problems by using cutting plane method. Nawkhass [7] investigated cutting plane technique and algorithm to solve an extreme point quadratic fractional programming problem for the special case. This paper presents definition of an EPMOLPP and suggested a new technique (HM approach) to transform an extreme point MOLPP to extreme point SOLPP and investigated. And with the alternative technique, to find the optimal solution and used Chandra Sen's approach to generate the best compromising optimal solution.
2. Extreme Point Linear Programming Problem
Extreme point linear programming problem can be formulated by Kirby, Love and Swarup [6] as follows: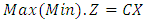 Subject to:
Subject to: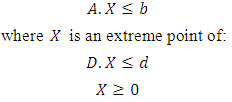 | (2.1) |
where C is n-dimensional vector of constants; 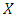 is n-dimensional vector of variables. A is
is n-dimensional vector of variables. A is 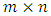 matrix of constants; b is m-dimensional vectors of constants. D is
matrix of constants; b is m-dimensional vectors of constants. D is 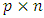 matrix of constants and d is
matrix of constants and d is 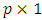 vector of constants.
vector of constants.
3. Alternative Approach to Solve (EPLP) Problems
Alternative approach to solve extreme point linear programming is based on simplex method, the procedure of this approach developed in [5].
3.1. Notations
First we consider the following problem instead of the problem (2.1).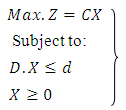 | (3.1.1) |
Let D1= set of all decision variables.Xi=set of all extreme points of the feasible region corresponding to all basic feasible solutions of (3.1.1) with initial entering variable xi into the basis till the end of all iterations including initial basic feasible solution.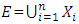 = set of all extreme points of the feasible region of (3.1.1).
= set of all extreme points of the feasible region of (3.1.1).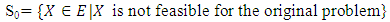
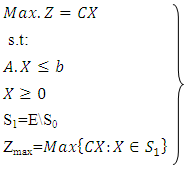 | (3.1.2) |
3.2. Algorithm
This algorithm can be summarized in the following steps:Step 1:Solve the problem (3.1.1) by using simplex method with entering variable xi, i=1…n and then obtain Xi.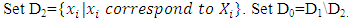 Step 2:If D0≠Ø, go to step1. Otherwise go to step3.Step 3:
Step 2:If D0≠Ø, go to step1. Otherwise go to step3.Step 3: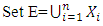 Step 4:Check whether each
Step 4:Check whether each 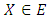 is feasible or not for the problem (3.1.2) to obtain S0.Step 5:Set S1=E\S0.Step 6:Calculate the value of Z at each extreme point
is feasible or not for the problem (3.1.2) to obtain S0.Step 5:Set S1=E\S0.Step 6:Calculate the value of Z at each extreme point 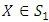 and determine the optimal value of the objective function among these values of Z.Step 7:Say, Z is optimal at X0 and the optimal value is Zmax.
and determine the optimal value of the objective function among these values of Z.Step 7:Say, Z is optimal at X0 and the optimal value is Zmax.
4. Mathematical Form of an (EPMOLPP)
Extreme point multi-objective linear programming problem can be defined as follows: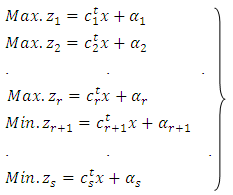 | (4.1) |
Subject to: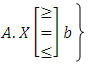 | (4.2) |
where 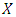 is an extreme point of ?
is an extreme point of ?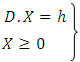 | (4.3) |
where r is the number of objective functions to be maximized, s is the number of objective functions to be maximized and minimized, (s-r) is the number of objective functions to be minimized, X is an n-dimensional vector of decision variables, C is n-dimensional vector of constants and 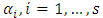 are scalar constants. Other symbols have been the same meaning section (2).
are scalar constants. Other symbols have been the same meaning section (2).
5. Chandra Sen's Technique to Solve EPMOLPP
The combined objective functions of Chandra Sen's techniques are shown in equation (5.1)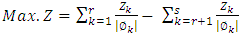 | (5.1) |
and solved it by alternative method with the same constraints (4.2) and (4.3).Suppose we obtain a single value corresponding to each of the objective functions of the MOLPP of equation (4.1) they are being optimized individually subject to the constraints (4.2) and (4.3) as in equation 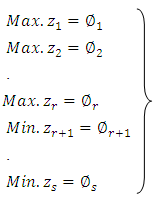 | (5.2) |
where 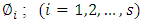 are the values of objective functions. After that by alternative approach solve this problem we obtain an extreme point for optimal solution.
are the values of objective functions. After that by alternative approach solve this problem we obtain an extreme point for optimal solution.
5.1. Algorithm of Chandra Sen's Technique
An algorithm for obtaining the optimal solution for the MOLPP definition equation (4.1) can be summarized as follows:Step 1:Determined values to each of the individual objective functions which to be maximized and minimized.Step 2:Solve the first objective problem by alternative approach with constraints (4.3).Step 3:Check the feasibility of the solution in step 2, if it is feasible then go to step 4, otherwise, use dual simplex method to remove infeasibility.Step 4:Marking a name to the optimum value of the first objective function to 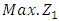 called
called 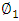 .Step 5:Repeat the step 2, i=1,…,r for the kth objective function, for all i=i+1,…,sStep 6:Determine Chandra Sen's technique.Step 7:Optimize the combined objective function (5.1), under the same constraints (4.3), by repeating Steps 2-4.
.Step 5:Repeat the step 2, i=1,…,r for the kth objective function, for all i=i+1,…,sStep 6:Determine Chandra Sen's technique.Step 7:Optimize the combined objective function (5.1), under the same constraints (4.3), by repeating Steps 2-4.
6. Theorem
Let 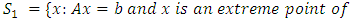
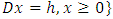 and
and 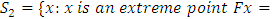
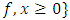 then
then 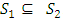 .Proof: see [3]
.Proof: see [3]
7. Harmonic Mean Technique to Solve (EPMOLPP)
In class EPMOLPP have various techniques for optimal solve. We can here transforming this problem of multi to single by HM technique first time find optimal solution by alternative approach for each objective function in the problem, next time by our technique (HM) transforming to single then by the same alternative approach. We given optimal solution this time, we can comparison with Chandra Sen approach.The combined objective functions of Harmonic Mean technique as shown in equation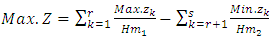 | (7.1) |
subject to constraints (4.2) and (4.3).
7.1. Notations
The following notations were used in our algorithm: 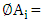 The value of objective function which is to be maximized.
The value of objective function which is to be maximized.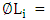 The value of objective function which is to be minimized.
The value of objective function which is to be minimized.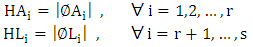 Hm1= The value of Harmonic mean of maximized.Hm2=The value of Harmonic mean of minimized.
Hm1= The value of Harmonic mean of maximized.Hm2=The value of Harmonic mean of minimized.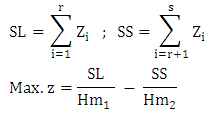
7.2. Algorithm
We summarize the following algorithm to get the optimal solution of EPMOLPP as follows:-Repeat steps (1-5) in section (5.1)Step 6:Determine Harmonic Mean Hm1 for 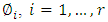 and Hm2 for
and Hm2 for 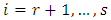 Step 7:Optimize the combined objective function
Step 7:Optimize the combined objective function 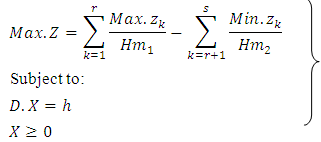 | (7.1.1) |
Step 8:Solve problem (7.1.1) by Alternative approach in [5].
8. Numerical Examples
We constructed some numerical examples to illustrate the techniques for solving EPMOLPPExample (8.1):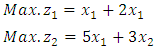 Subject to:
Subject to: 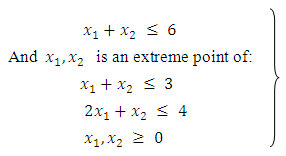 | (8.1) |
SolutionWe solve each of objective function with the same constraints by alternative method algorithm in section (3.2) the results in table below:Table (8.1). Results of Example (8.1)
 |
| |
|
First we use the harmonic mean (HM) technique to translate the problem from an extreme point multi objective linear programming problem to an extreme point single objective linear programming problem. Then we solve the example (8.1) by using formula (7.1). The results are shown table (9.1).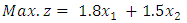 Subject to constraints (8.1) The above problem was solved by alternative approach, and obtained
Subject to constraints (8.1) The above problem was solved by alternative approach, and obtained 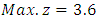 at the extreme point
at the extreme point 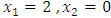 .Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, we obtain:
.Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, we obtain: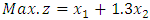 Subject to constraints (8.1)Solving this problem by the alternative approach and obtained
Subject to constraints (8.1)Solving this problem by the alternative approach and obtained 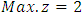 at the extreme point
at the extreme point 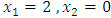 .Example (8.2)
.Example (8.2)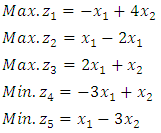 Subject to:
Subject to: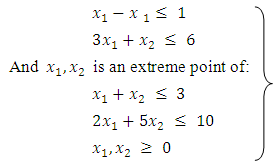 | (8.2) |
SolutionWe solve each of objective function with the same constraints by the alternative method algorithm in section (3.2) the results in table (8.2):Table (8.2). Results of Example (8.2)
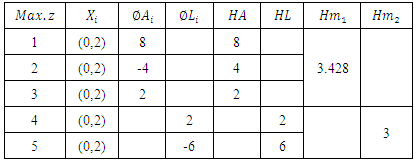 |
| |
|
First, we use the harmonic mean (HM) technique to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem. By using formula (7.1) the problem becomes: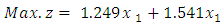 Subject to constraint (8.2) We solved by the alternative approach and we obtained
Subject to constraint (8.2) We solved by the alternative approach and we obtained 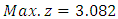 at the extreme point
at the extreme point 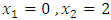 .Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, the problem becomes:
.Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, the problem becomes: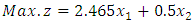 Subject to constraint (8.2)Solving this problem by the alternative approach, we obtained
Subject to constraint (8.2)Solving this problem by the alternative approach, we obtained 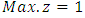 at the extreme point
at the extreme point 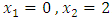 .
.
9. Conclusions
Two techniques, Chandra Sen's and Harmonic Mean are applied on both examples (8.1) and (8.2) to solve EPMOLPP. The comparison of these techniques are dependent on the value of the objective function and iteration, as is shown in table (9.1).Table (9.1). Comparison between results obtained by both techniques, using alternative technique
 |
| |
|
From the above table we can see the difference between the techniques in used each example.In example (8.1) our technique is (HM) where we got 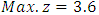 this consequence than other result which is obtained
this consequence than other result which is obtained 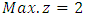 by Chandra Sen.In example (8.2) by using Harmonic Mean technique we obtained
by Chandra Sen.In example (8.2) by using Harmonic Mean technique we obtained 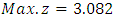 which is better than other result
which is better than other result 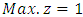 using Chandra Sen's technique. The comparison by iteration, when using alternative technique the iteration of both above examples (8.1) and (8.2) are greater than other technique.In each example we found that the best technique for transforming and solving EPMOLPP is the Harmonic Mean technique in each case it was better than Chandra Sen's technique.
using Chandra Sen's technique. The comparison by iteration, when using alternative technique the iteration of both above examples (8.1) and (8.2) are greater than other technique.In each example we found that the best technique for transforming and solving EPMOLPP is the Harmonic Mean technique in each case it was better than Chandra Sen's technique.
References
| [1] | Abdulrahim, B. K. (2014) "On Extreme Point Quadratic Fractional Programming Problem" Applied Mathematical Sciences, Vol. 8, 2014, no. 6, 261 – 277. |
| [2] | Frederick S. H., Gerald J. L., (2001) "INTRODUCTION TO OPERATIONS RESEARCH" Seventh Edition Published by McGraw-Hill, an imprint of The McGraw-Hill Companies, Inc., 1221. |
| [3] | Gupta, R. K. and Kanti S. (1978) "On Extreme Point Fractional Programming", Portugaliae Mathematica, Vol. 37, Fasc. 1-2. |
| [4] | Hamad-Amin, A.O. (2008) "An Adaptive Arithmetic Average Transformation Technique for Solving MOPP" M. Sc. Thesis, University of Koya, Erbil/Iraq. |
| [5] | Hossain, T.; Md. Arefin, R. and Md. Islam, A. (2015) "An Alternative Approach for Solving Extreme Point Linear and Linear Fractional Programming Problem" Dhaka Univ. J. Sci. Vol.63. No.2, pp 77-84. |
| [6] | Kirby, M.J.L. & Love, H.R. and Kanti, S. (1972) "Cutting Plan Algorithm for Extreme Point Mathematical Programming", Cashier. Ducentre D Etudes De Recherche Operationelle, Vol.14, No.1 pp 27-42. |
| [7] | Nawkhass M.A. (2014) "on solving quadratic fractional programming problems" MSc. Thesis, salahaddin university Erbil Iraq. |
| [8] | Salih, A. D. (2010) "On Solving Linear Fractional Programming Problems with Extreme points" M. Sc. Thesis, University of Salahaddin, Erbil/Iraq. |
| [9] | Sulaiman, N. A. (1989) "Extreme Point Quadratic Programming Techniques" M.Sc. Thesis, University of Salahaddin, Erbil/Iraq. |
| [10] | Sulaiman, N. A.; Abdullah, R. M. and Abdull, S. O. (2016) "Using Optimal Geometric Average Technique to Solve Extreme Point Multi- Objective Quadratic Programming Problems" Journal of Zankoi Sulaimani, Part- A. (Pure Applied Science). |


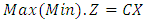 Subject to:
Subject to: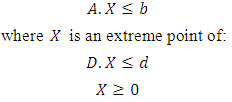
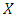 is n-dimensional vector of variables. A is
is n-dimensional vector of variables. A is  matrix of constants; b is m-dimensional vectors of constants. D is
matrix of constants; b is m-dimensional vectors of constants. D is 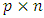 matrix of constants and d is
matrix of constants and d is 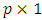 vector of constants.
vector of constants.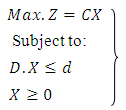
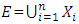 = set of all extreme points of the feasible region of (3.1.1).
= set of all extreme points of the feasible region of (3.1.1).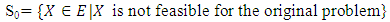
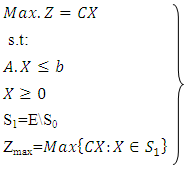
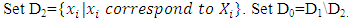 Step 2:If D0≠Ø, go to step1. Otherwise go to step3.Step 3:
Step 2:If D0≠Ø, go to step1. Otherwise go to step3.Step 3: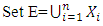 Step 4:Check whether each
Step 4:Check whether each 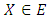 is feasible or not for the problem (3.1.2) to obtain S0.Step 5:Set S1=E\S0.Step 6:Calculate the value of Z at each extreme point
is feasible or not for the problem (3.1.2) to obtain S0.Step 5:Set S1=E\S0.Step 6:Calculate the value of Z at each extreme point 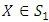 and determine the optimal value of the objective function among these values of Z.Step 7:Say, Z is optimal at X0 and the optimal value is Zmax.
and determine the optimal value of the objective function among these values of Z.Step 7:Say, Z is optimal at X0 and the optimal value is Zmax.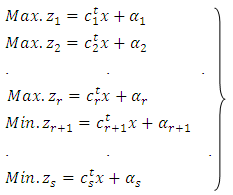
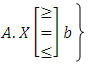
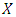 is an extreme point of ?
is an extreme point of ?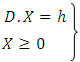
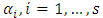 are scalar constants. Other symbols have been the same meaning section (2).
are scalar constants. Other symbols have been the same meaning section (2).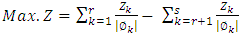
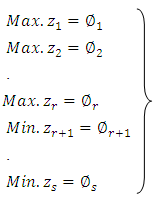
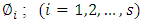 are the values of objective functions. After that by alternative approach solve this problem we obtain an extreme point for optimal solution.
are the values of objective functions. After that by alternative approach solve this problem we obtain an extreme point for optimal solution.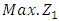 called
called 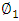 .Step 5:Repeat the step 2, i=1,…,r for the kth objective function, for all i=i+1,…,sStep 6:Determine Chandra Sen's technique.Step 7:Optimize the combined objective function (5.1), under the same constraints (4.3), by repeating Steps 2-4.
.Step 5:Repeat the step 2, i=1,…,r for the kth objective function, for all i=i+1,…,sStep 6:Determine Chandra Sen's technique.Step 7:Optimize the combined objective function (5.1), under the same constraints (4.3), by repeating Steps 2-4.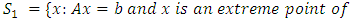
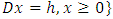 and
and 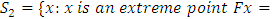
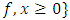 then
then 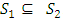 .Proof: see [3]
.Proof: see [3]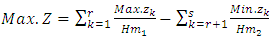
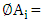 The value of objective function which is to be maximized.
The value of objective function which is to be maximized.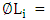 The value of objective function which is to be minimized.
The value of objective function which is to be minimized.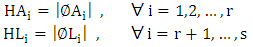 Hm1= The value of Harmonic mean of maximized.Hm2=The value of Harmonic mean of minimized.
Hm1= The value of Harmonic mean of maximized.Hm2=The value of Harmonic mean of minimized.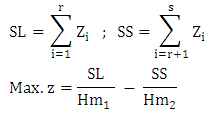
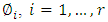 and Hm2 for
and Hm2 for 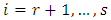 Step 7:Optimize the combined objective function
Step 7:Optimize the combined objective function 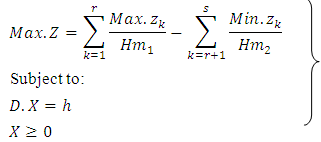
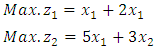 Subject to:
Subject to: 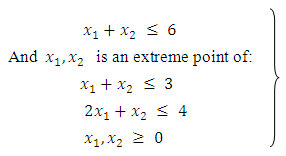
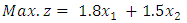 Subject to constraints (8.1) The above problem was solved by alternative approach, and obtained
Subject to constraints (8.1) The above problem was solved by alternative approach, and obtained 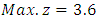 at the extreme point
at the extreme point 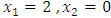 .Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, we obtain:
.Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, we obtain: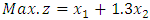 Subject to constraints (8.1)Solving this problem by the alternative approach and obtained
Subject to constraints (8.1)Solving this problem by the alternative approach and obtained 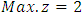 at the extreme point
at the extreme point 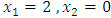 .Example (8.2)
.Example (8.2)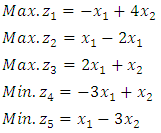 Subject to:
Subject to: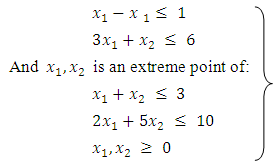
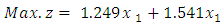 Subject to constraint (8.2) We solved by the alternative approach and we obtained
Subject to constraint (8.2) We solved by the alternative approach and we obtained 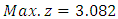 at the extreme point
at the extreme point 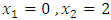 .Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, the problem becomes:
.Using Chandra Sen's approach technique in formula (5.1) to translate problem from an extreme point multi objective linear programming problem to extreme point single objective linear programming problem, the problem becomes: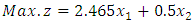 Subject to constraint (8.2)Solving this problem by the alternative approach, we obtained
Subject to constraint (8.2)Solving this problem by the alternative approach, we obtained 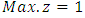 at the extreme point
at the extreme point 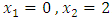 .
.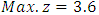 this consequence than other result which is obtained
this consequence than other result which is obtained 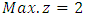 by Chandra Sen.In example (8.2) by using Harmonic Mean technique we obtained
by Chandra Sen.In example (8.2) by using Harmonic Mean technique we obtained 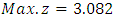 which is better than other result
which is better than other result 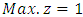 using Chandra Sen's technique. The comparison by iteration, when using alternative technique the iteration of both above examples (8.1) and (8.2) are greater than other technique.In each example we found that the best technique for transforming and solving EPMOLPP is the Harmonic Mean technique in each case it was better than Chandra Sen's technique.
using Chandra Sen's technique. The comparison by iteration, when using alternative technique the iteration of both above examples (8.1) and (8.2) are greater than other technique.In each example we found that the best technique for transforming and solving EPMOLPP is the Harmonic Mean technique in each case it was better than Chandra Sen's technique. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

