1. Introduction

In an earlier article [1] it was reported that the mean radius method that can be used to construct an external tangent to touching or isolated circles failed when applied to intersecting circles because the point which should be on the expected tangent fell inside the larger circle. Therefore there is the need for continued investigation to solve this problem. This paper reports the use of mean radius with radical axis in constructing an external tangent to two intersecting circles. The method also is applicable to touching and isolated two circle systems. A radical axis, in the case of a two circle systems, is a straight line from which equal tangents can be drawn to the two circles. With touching circles, figure 1, the internal common tangent, PCQ, is a radical axis which was called a “lead tangent” in an earlier article [1] while for intersecting circles, figure 1, the radical axis PQ, is the straight line passing through the points of intersection of the two circles and is perpendicular to AB at C. Radical axis is always perpendicular to the line of centres of the two circles. For simplicity, hereafter, circle A is the circle with center A and radius r_A and the straight line joining the centres of circles A and B is the centre line or line of centres.

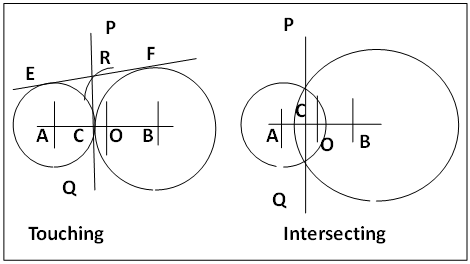Figure 1. Radical Axis (PQ) of touching and interesting Circles

2. Methodology

2.1. Constructing a Tangent to Intersecting Circles by the Mean Radius Radical Axis Method, figure 2

(a). Draw the intersecting circles A and B, join the centres A and B. Join the intersecting points producing both ways to P and Q. PQ is the radical axis and is perpendicular to AB.

(b). Determine the midpoint O of AB and also the mean radius (r_A + r_B)/2 by bisection.

(c). Centre O and radius (r_A + r_B)/2 cut PQ at R. R is a point on the radical axis from which equal tangents as parts of the common tangent to circles A and B can be drawn.

(d). Draw the semicircle with AR as diameter to cut circle A at E and the semicircle with BR as diameter to cut circle B at F. Join EF producing both ways as the required tangent.

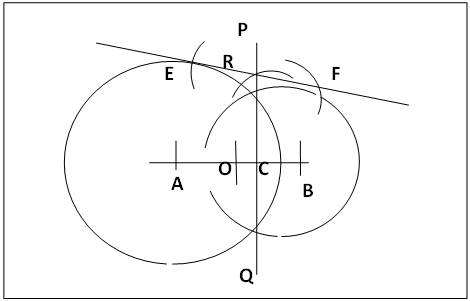Figure 2. Mean Radius /Radical Axis Procedure for tangent to intersecting Circles

3. Results and Discussion

The earlier reported [1] failure in the use of mean radius in constructing external tangent to two intersecting circles was later found to arise from the use of the internal homothetic point and the midpoint of AB as centres and with mean radius as the radius to locate the needed point on the tangent being looked for as is in the case with isolated circles. Realizing latter that the common chord in the intersecting circles, figure 1, is a radical axis just as the common internal tangent in touching circles, figure 1, the mean radius was used, with O as centre, figure 2, to cut the common chord (produced) to obtain the needed special radical point (a homothetic point also) as was the case in touching circles. In figure 1, point O is the midpoint of AB, so AO = OB = (r_A + r_B)/2. Thus the radius used to locate R along PQ, the radical axis, is mean radius. Therefore one expects that the use of these elements in similar manner in intersecting circles will give the same result and that turned out to be the case. Thus this method resolved the problem.

3.1. Importance of the Radical Axis

As earlier stated, from the radical axis equal tangents to two circles can be drawn, therefore on each side of the line of centres there is a special point along the radical axis in which the two equal tangents form a straight line. That is the special point on the radical axis is the midpoint of a common tangent to the two circles. Each of these two special points is also a special homothetic centre in addition to the homothetic centres located along the line of centres. A common external tangent to the two circles can be constructed from any of these special points as external point by the routine method.

3.2. Locating the Radical Axis and the Special Radical Point on the Radical Axis in two Circle Systems

Constructing a radical axis in touching or intersecting circles is a routine and easy geometric process from figure 1. For isolated circles, figure 3, the radical axis was by intuition located, in an earlier paper [1], as the perpendicular bisector of the midpoint O of the line of the centres and the internal homothetic point C. This method eventually provided a procedure for the determination of the radical axis in a system of two isolated circles. The special radical point in the said paper [1] was also intuitively obtained by letting the arcs of same radii (r_A + r_B)/2 and from centres O and C intersect at R i.e. R is along the perpendicular bisector of OC thus proving the procedure correct.

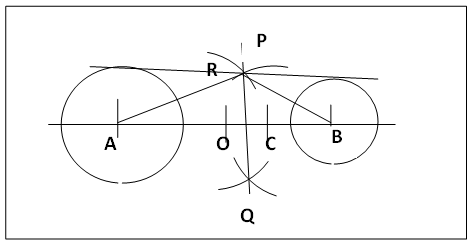Figure 3. Locating Radical axis for Isolated Circles

The straight line PRQ, figure 3, is the radical axis of these isolated circles as seen above. The needed point R can be located along PQ by using O as centre and with radius (r_A + r_B)/2 to cut PQ at R. Equal tangents drawn from R to the two circles will form a common tangent. This is the principle applied in all the cases of systems of two circles for constructing a common tangent by the mean radius radical axis method.

For any two circle systems, touching, isolated and intersecting, including cases with r_A = r_B, radical axis and mean radius can be used to locate a special point R as an external point on the radical axis from which equal tangents to two circles can be constructed by routine procedure. The equal tangents form a common tangent to the two circles showing that the special radical points (one on each side of the centre line) are another set of homothetic centres. The general procedure for all two circle systems is to cut the radical axis (determined) at point R with the mean radius (r_A + r_B)/2 (of the circles) using centre O (the midpoint of centre line). This is the principle used in the construction of external tangent to touching and isolated circles in the said earlier paper [1] and to intersecting circles in this present article.

This principle was used in the case of touching circles and isolated circles earlier published [1] although radical axis which was not mentioned was first determined by the bisection of the straight line joining the internal homothetic point C and the midpoint O of the line of centres..

This mean radius/radical axis method added to the radius difference method [2, 3] and external homothetic centre method [4], excluding a general method, increased the number of methods for constructing external tangent to two intersecting circles. This work has also shown that the radical axis of isolated circles can be located by the bisection of the straight line joining the midpoint of the centres of the circles and the internal homothetic point.

4. Conclusions

Mean radius is an important element in determining the radical axis of isolated circles and when combined with radical axis the two elements locate the special radical point through which common external tangent can be drawn to circles in any systems of two circles.

The work also has revealed the existence, for two circle systems, two sets of homothetic points; a set occurs along the line of centers (produced) and the other set along the radical axis. The latter set can replace the external homothetic point of the former set in the construction of common external tangent to any two circle system. Its use eliminates the large space required in constructing external tangent in systems of circles with widely separated centres or with nearly the same radii.