Ohochuku N. Stephen
Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Nigeria
Correspondence to: Ohochuku N. Stephen, Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Presently there are two methods available for constructing a common tangent to some systems of two circles. Three additional methods one each for systems of two touching and the other for systems of two isolated circles and also a new general approach to all systems of two circles are here introduced. The additional methods are simple and should be introduced and taught alongside the present methods.
Keywords:
Tangents two circles alternative methods
Cite this paper: Ohochuku N. Stephen, Tangent to Two Circles: Additional Methods of Approach, Applied Mathematics, Vol. 6 No. 4, 2016, pp. 73-77. doi: 10.5923/j.am.20160604.02.
1. Introduction
In circle geometry, a tangent is defined as a straight line that touches a circle at a point on the circumference [1] of the circle and the construction has always involved drawing a straight line perpendicular to the terminus of a radius at the circumference of the circle. This course of action works fine with single circle but requires application of other principles when a system of two circles is involved. A system of two circles can be touching as in figure 1(a) and (b) or isolated as in figure 1(c) or intersecting as in figure 1(d). The system of two touching circles have two sub groups viz circles touching internally (a) or externally (b) while the systems of isolated (c) and intersecting (d) circles have no sub groups. Systems of internally touching circles have two types of common tangents, PQ (external) and RS (internal) as in isolated circles, while externally touching circles have only one type of tangent as is in intersecting circles. Two circles touch internally if the point of touch C is in between the centres and externally if the point of touch is on the line of centres produced. Also a tangent (RS) is internal when its point of intersection with the line of centres is between the centers and external when (PQ) cuts across the line of centres produced. Hitherto a circle designated as circle A is the circle with centre A and radius rA and the distance between the centers of circles A and B is described as centre distance or line of centres AB. The two basic methods in use are referred to here as the difference in radii (for external)/sum of radii (for internal) tangents [2, 3] and use of homothetic centre [4] (for both external and internal) tangents, figures 2 and 3 show the sketches of the construction of external tangents to internally touching circles, isolated circles and intersecting circles bythese methods while figure 4 shows secant, homothetic centres and use for drawing external and internal tangents to isolated circles [4]. All these methods fail when applied to the construction of internal tangent to internally touching circles figure 1a, the external tangent to externally touching circles figure 1b and any of the systems in which the two circles are of equal radius. Therefore there is need to search for more method(s) for constructing common tangents to two circle systems some of could be suitable for drawing a common tangent to all the four various systems of two circles including the cases where the circles are of equal radius and if possible the method could be applicable to the construction of a tangent to a single circle. This work introduces two additional methods specific to touching and isolated two circle systems and also a method generally applicable to constructing a common tangent to all systems of two circles that could have equal radii and also to a single circle.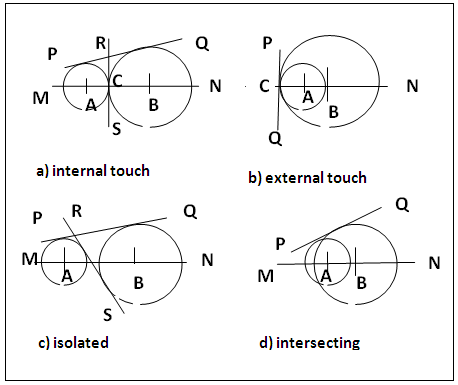 | Figure 1. Types of systems of two Circles and of Tangents |
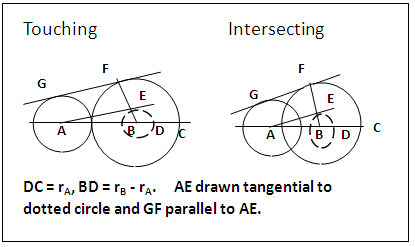 | Figure 2. Radius Difference Method illustrated with External Tangent to systems of internally touching and intersecting Circles |
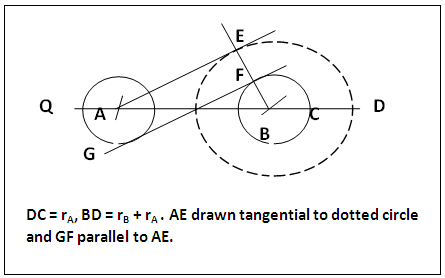 | Figure 3. Sum of Radii Method illustrated with Internal Tangent to a system of isolated Circles [2, 3, 4] |
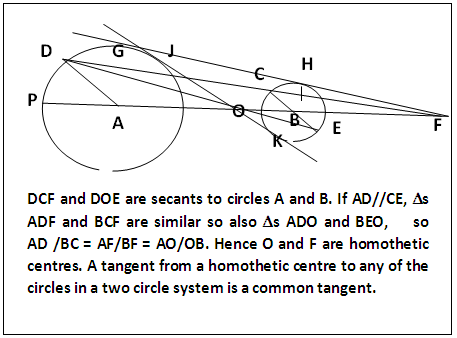 | Figure 4. Secant, Homothetic Centre and their Use in drawing Internal and External Tangents [4] illustrated with isolated circles |
2. Methods
2.1. Additional Methods for two Circle Systems
2.1.1. External Tangent to Two touching Circle system figure 5.In figure 5, circles A and B touch at C.(a). CR is drawn tangential to both circles at C.(b). D is the intersection of the tangent at C and the semicircle with AB as diameter. (c). AD and DB are joined. PD is drawn tangential at E to circle A using AD as diameter and DQ tangential at F to circle B using BD as diameter. PEDFQ is a straight line tangent to circles A and B.Alternatively in figure 5:With point D known from steps (a) and (b) above, centre D and radius DC circle A is cut at E and circle B at F. EF is tangential to the two circles. Alternatively again in figure 5: Having got point D from steps (a) and (b) from section 2.1.1a above, ∠ADP is constructed equal to ∠ADC. Similarly ∠BDQ is constructed equal to ∠BDC. PD touches circle A at E and DQ touches circle B at F. PQ is the required tangent.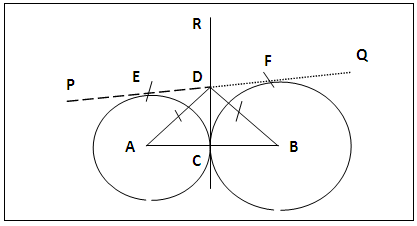 | Figure 5. External Tangent to Two touching Circles |
2.1.2. External Tangent to Two isolated or touching Circles: mean Radius Method, figure 6.Two types of tangents can be drawn to two isolated circles viz one external and one internal tangent, figure 6a, b. For external tangent, the method is as follows.(a). Divide, by parallel line method or otherwise, the centre line AB of the circles at C (internal homothetic point) such that AC/CB = rA/rB and bisect AB at O.(b). Centre C and radius (rA + rB)/2 swing an arc above AB; centre O with same radius cut the first arc at D. D is a point on the required tangent PQ to be constructed.(c). If AD and BD are respectfully joined and each used as a diameter, their respective semicircles will cut circle A at E and circle B at F. PQ is tangential to circle A at E and circle B at F, EF is the external tangent to the circles, figure 6a. 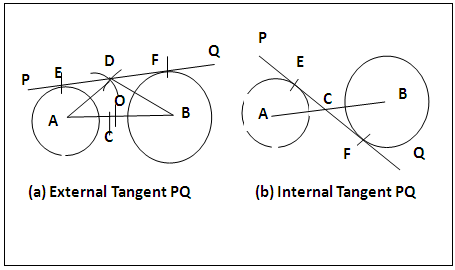 | Figure 6. Mean radius Method illustrated with Tangent to Two isolated Circles |
2.2. The New General Method figure 7.
The method goes as follow.(a). Draw the straight line PQ which will eventually be the required tangent.(b). At a point C on PQ erect a perpendicular CE. Centre C radius rA cut CE at A. Centre A and radius rA describe circle A. (c). Centre A and radius AB (the centre distance) swing a long arc MN. Anywhere along PQ, say at F, erect another perpendicular FG. C as centre and radius rB cut CE at H, F as centre and same radius rB cut FG at J. Join HJ producing if necessary to cut arc MN at B (the centre of circle B).(d). Centre B and radius rB describe circle B which will touch PQ at D. PQ is a tangent to circles A and B.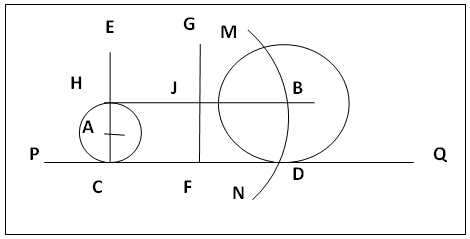 | Figure 7. New General Method for drawing a Tangent to any system of two Circles illustrated with isolated Circles |
2.3. Extension of the new General Method to other Circle Systems
2.3.1. Tangent at a Point on the circumference of a Single CircleThe starting point in the use of the new general approach is the construction of a tangent to a single circle, section 2.2 steps (a) and (b).2.3.2. Tangent from an outside Point to a Circle, Figure 8.(a). Having done section 2.2.1a, choose a point O on PQ. OQ is the tangent from O to circle A.2.3.3. Intersecting Tangent from a Point to a Circle, figure 8.Carry out section 2.2.1b. O as centre and radius OB cut circle A at C. Join OC producing to R. OQ and OR are the intersecting tangent from O to circle A.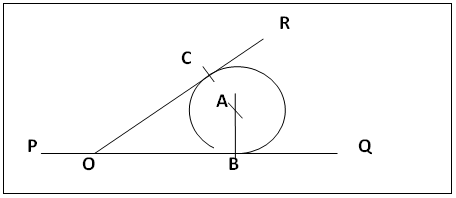 | Figure 8. Application to drawing intersecting Tangents to a given Circle |
2.3.4. To draw Tangents intersecting at a given Angle Ɵ to a single Circle, figure 9.(a). Mark point O on a straight line PQ and construct ∠SOQ equal to the given angle Ɵ and let OR be the bisector of ∠SOQ.(b). At convenient points C and D, erect perpendiculars and cut CE = DF = rA. Join FE producing to cut OR at A. Describe circle A with centre A and radius rA, it touches PQ at B and OS at G. 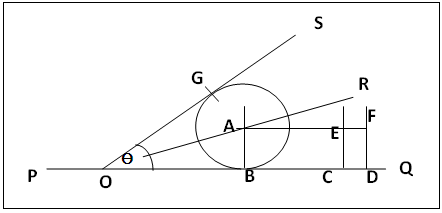 | Figure 9. To draw Tangents intersecting at a given Angle Ɵ to a single Circle |
2.4. An Array of Circles having different Placements to one another and with a common Tangent Figure 10.
The new method can be applied to drawing a common tangent to an array of circles with pairs of touching (circles A and B), isolated (circles A and C, A and D) and intersecting (circles B and C) circles using the same procedure. Figure 10 shows what is obtained in such a construction.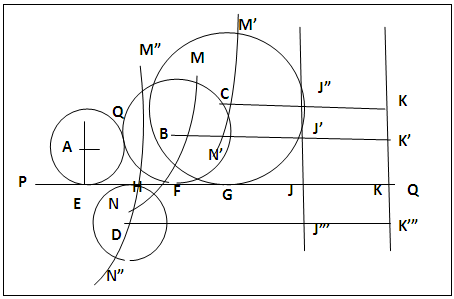 | Figure 10. Array of Circles |
Table 1 shows the properties of the circles in the array.Table 1. Parameters of pairs of Circles used in drawing the common Tangent PQ in figure 10
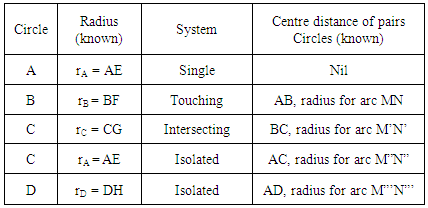 |
| |
|
3. Results and Discussion
3.1. Tangents to single Circle and to two Circles by the current Methods
A tangent to a single circle can be drawn at any point on the circumference of the circle or from any point outside the circle but this is not so with two circles in different placements. With two circles, a common tangent is restricted to a pair of points each point on each circle. Hence the method for single circle will not be applicable without modifications which will vary depending on whether the tangent is external or internal. The two methods available, to the best of our knowledge, are not published.That is why the essential details are given in the relevant figures. The methods are not applicable to drawing the tangent to touching circles at the point of touch hence the method used for single circle are always adopted. The existing methods reduce the procedures to drawing a tangent to a circle from an external point (as in single circles) and which at times is a homothetic point. The method utilizing eternal homothetic centre needs large space for the external tangent. 3.1.2. Additional Methods for two Circle SystemsIn the two touching circle system figure 5 section 2.1.1a,D is a point from which tangents can be drawn to circles A and B and since DC is a common tangent to both circles, DA = DC = DB. As point D is at the circumference of the semicircle with AB as diameter, angle ADB is 90o and angle PDA + angle QDB is also 90o because angle PDA = angle ADC. Similarly angle QDB = angle BDC and also DC = DE = DF (all properties of intersecting tangents). So PDQ is a straight line.A point to note here is that any point on a common tangent to two circles can be used as an external point to draw the common tangent. Examples of such points are the homothetic points O and F in figure 4; other points are D in figure 5 and point D in figure 6a. The location of any of these points in absence of the common tangent is achieved by the processes indicated in the relevant sections containing the cited figures. In the mean radius method, figure 6 section 2.1.1b, it can be shown by construction that point D on a common tangent to two circles is the only point equidistant by (rA + rB)/2 from points C and O. Mean radius method fails with intersecting circles because point D may lie inside the larger circle. In the case of touching circles, section 2.2.1a figure 5, CR is a “lead tangent” that makes the three alternative procedures possible in applying the basic facts of tangent in the constructions. PQ is a straight line because ∠CDA = ∠ADP and ∠CDB = ∠BDQ. ∠ADB = 90° hence ∠ADP + ∠BDQ = 90o. So ∠CDP and ∠CDQ are supplementary. As the two last angles share common arm CD, PEDFQ is a straight line. Also as DC = DP = DQ, a tangent common to circle A and circle B can be drawn by cutting circles A and B with centre D and radius CD at E and F respectively. Alternatively ∠CDP is constructed equal to ∠CDA and ∠CDQ constructed equal to ∠CDB. The arm DP will touch circle A at E and DQ will touch circle B at F. A third method uses AD and BD as diameters whose respective semicircles cut circle A at E and circle B at F.
3.2. The General Approach: The New Method
The new method is based on an alternate definition of tangent to a circle as a straight line which a circle touches and suggesting that a straight line that will eventually become the tangent be drawn then followed by the tangential circle. This is the reverse of the existing procedure. Having drawn the first circle A, the locus of the second circle B lies on a circle with radius AB. The centre of circle B is fixed by the intersection of a perpendicular to PQ and of radius rA. These simple facts of geometry make the method applicable to all types of tangents to any arrangement of two circles, Table 2, even where the circles are of same radii. Large space is not required as in locating external homothetic centres. The method is not restricted to drawing tangents to two circle systems. It is applicable to tangents to single circles and systems of circles of varying placements all sharing one common tangent.Table 2. Methods applicable to drawing Tangents to two Circle Systems
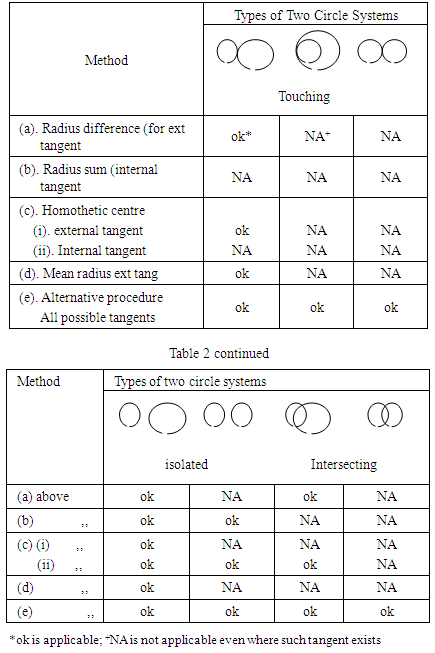 |
| |
|
The method is simple to manipulate. It uses mainly parallel perpendicular lines with fewer arcs so it gives a clearer figure. The method can be applied in the construction of two lines ending as tangents to an arc of a circle, figure 10. The procedure is clear and within the level of high (secondary) school work scheme. The alternative approach is applicable to systems of one or two circle systems or an array of circles sharing a common tangent.
4. Conclusions
The additional methods for system of two touching and also isolated circles increase the number of methods using the existing procedures. The mean radius method to isolated circles provides a procedure that does not need large space for external tangent as is the case with homothetic procedure.The alternative definition of a tangent to a circle has made possible the generation of this new alternative approach that turns out to be a general method of constructing a tangent to a circle or two circles in varied placements. The method is also applicable to an array of circles that share a common tangent. The new method is simple to operate, general and versatile but with all its versatility, it should be seen as complementary to the orthodox method and should be taught pari passu with the existing procedures.
References
| [1] | Channon. J. A, A. Mcleish Smith, H. C. Head, A. O. Kalejaiye and M. F. Macrae. New General Mathematics for West Africa Senior Secondary 2. Longman Group. U K Ltd, 3rd edition 1989, reprinted 1990, p85. |
| [2] | Answers. Construction of the Common Tangents to 2 Circles. jiguanglaoshi@ gmal.com accessed 19 April 2016. |
| [3] | Jeff Kertsher. Tangent Lines to two Circles. http://jwilson.coe.uga.edu/emt669.student.Folder/Kertcher Jeff/(essay.3/ext.tan.gsp) April 2016. |
| [4] | A Bogometry, How to Construct common Tangent to Two Circles from interactive Mathematics Miscellany and uzzles. http://www.cut-the-knot.org(Curriculum/Geometry/GeoGebr a) Tangent to two circles.shtml. http://www.cut-the-knot.org(Curriculum/Geometry/GeoGebr a) Tangent to two circles.shtml) accessed 19 April 2016. |













 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
