Bolarin G., Omatola I. U.
Department of Mathematics, Federal University of Technology, Minna, Nigeria
Correspondence to: Bolarin G., Department of Mathematics, Federal University of Technology, Minna, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this work we developed and analyzed a mathematical model of HIV/TB co infection. The model is a first order Ordinary Differential Equations, in which the human population is divided into six mutually- exclusive compartments namely; TB- Susceptible individuals (S), TB-Infected individuals (I), TB-Recovered individuals (R), HIV-Infected individuals (P1), Co- Infected individuals (P2) and individuals with AIDS (A). The equilibrium states were obtained and their stabilities were analyzed by using Bellman and Cooke’s theorem. The result shows that the endemic equilibrium state is stable and the disease free equilibrium state will be stable if 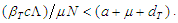
Keywords:
Tuberculosis, Human Immunodeficiency Virus, Co infection, Treatment, Equilibrium, Stability
Cite this paper: Bolarin G., Omatola I. U., A Mathematical Analysis of HIV/TB Co-Infection Model, Applied Mathematics, Vol. 6 No. 4, 2016, pp. 65-72. doi: 10.5923/j.am.20160604.01.
1. Introduction
Tuberculosis (TB) is a bacterial disease caused by Mycobacterium tuberculosis (tubercle bacilli). Transmission of TB occurs by air borne infectious droplets [13]. It typically affects the lungs (pulmonary TB) but can affect other parts as well (extra pulmonary TB) [10]. The World Health Organization (WHO) declared TB in 1993 has a global emergency. Nigeria ranks 10th among the 22 high burden in the world [11]. TB is preventable and curable. A mathematical model for TB has been a useful tool in accessing the spread of the disease, as well as its control. See [3] for example. HIV stands for Human Immunodeficiency Virus. HIV is a virus that gradually attacks the immune system and the immune system is our body’s natural defence against illness. If a person becomes infected with HIV, he or she will find it hard to fight off infections and diseases. The virus destroys a type of white blood cell called T-helper cells and makes copies of it inside them. T-helper cells are also referred to as CD4 cells [16]. There is no cure or vaccine for AIDS [5]. However, antiretroviral (ART) treatment improves health, pro-longs life, and substantially reduces the risk of HIV transmission. In both high-income and low-income countries, the life expectancy of patients infected with HIV who have access to ART is now measured in decades, and might approach that of uninfected populations in patients who receive an high HIV treatment [5].Co-infection of TB and HIV is when someone has both HIV and TB infections. When someone has HIV and TB, HIV infection accelerates the activation of tuberculosis and tuberculosis increases the rate at which HIV infection develops into AIDS [9]. It is worthy of note that HIV infection and infection with TB bacteria are two different infections as established in [6]. Co-treatment of HIV related TB improves survival especially in patients with CD4 counts <50 ells/mm3 [8]. Globally, one-third of the 34 million people living with HIV are infected with TB [14]. In 2014, about 400 000 people who had both TB and HIV were estimated to have died, in addition to the 1.1 million people who died from TB alone and 800 000 deaths from HIV alone. So in 2014 more people died from TB than from HIV related infections [15].[2] in his work, formulated a sex-structured model to capture the effect of complacency on the dynamics of HIV/AIDS but did not include how TB will affect the mix. But, recently a lot of great work has been done in the mathematical modelling of co infection of different pathogens though very little was done in the modelling of HIV-TB co infection. [13], [12], [6], [7] developed a mathematical model of HIV/TB co infection under TB treatment. Their work did not include anti-HIV treatment. [4] Developed a TB-HIV/AIDS co infection model and optimal control treatment. In this paper we incorporate all aspects of TB transmission dynamics as well HIV transmission dynamics to come up with a mathematical model of HIV/TB co-infection. This paper incorporate antiretroviral therapy for individuals infected with HIV. We investigate the effect of treatment on the TB in HIV/TB co infection and also investigate the effect of co treatment of HIV/TB co infection.The paper is organized as follows. Section 1 is introduction. The model formulation, the positive invariant region, the positivity of solutions, equilibrium states and the basic reproduction number are obtained in Section 2. The stability analysis of the model and concluding remark are carried out in sections 3 and 4 respectively.
2. Model Formulation
The model subdivides the human population into six mutually –exclusive compartments, Namely TB-susceptible individuals (S), TB-infected individuals who have active TB diseases and infectious (I), TB-recovered individuals (R), HIV-infected individuals (P1), co-infected individuals (P2) and full blown AIDS (A).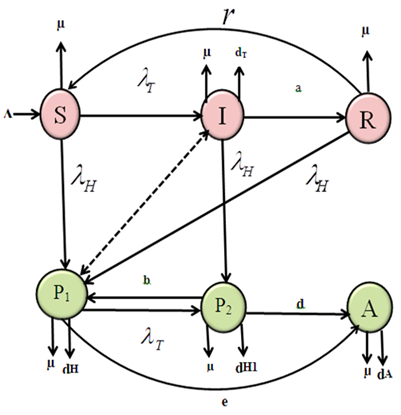 | Figure 1. The diagram for the flow of the model |
2.1. Basic Assumptions
Ø Individuals can only get TB through contact with TB infectious individuals (I and P 2).Ø Individuals may become HIV infected only through contact with HIV infectious individuals (P1 and P2).Ø The infectious I, both TB and HIV infectious P2 and AIDS individuals are considered too ill to remain sexually active and they are unable to transmit HIV through sexual activity. 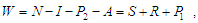 is the active population.To represent this mathematically, we have the following system of differential equations:
is the active population.To represent this mathematically, we have the following system of differential equations: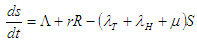 | (2.1) |
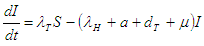 | (2.2) |
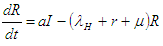 | (2.3) |
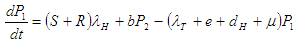 | (2.4) |
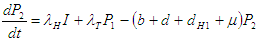 | (2.5) |
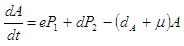 | (2.6) |
Where N=S+I+R+P1+P2+A.The force of infection, associated with TB infection is 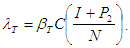 The force of infection
The force of infection 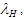 associated with HIV infection is
associated with HIV infection is 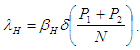
Table 1. Definition of State Variables and Parameters Used in the TB/HIV Model
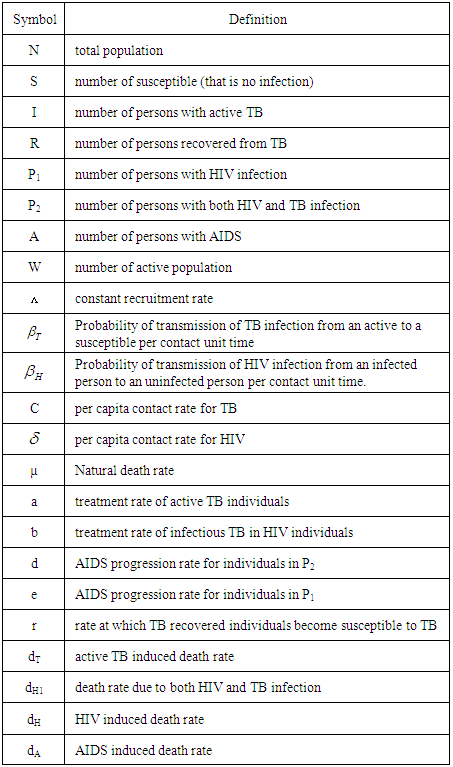 |
| |
|
2.2. The Positive Invariant Region
The total population size is 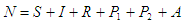 | (2.7) |
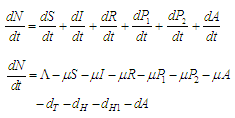 | (2.8) |
The positive invariant region can be obtained by using the following theorem.Theorem 2.1The solutions of the system of equations (2.1) to (2.6) are feasible for  if they enter the invariant region D.ProofLet
if they enter the invariant region D.ProofLet 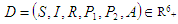 be any solution of the system of equations (2.1) to (2.6) with non-zero initial conditions.Assuming there is no disease equation (2.8) now becomes
be any solution of the system of equations (2.1) to (2.6) with non-zero initial conditions.Assuming there is no disease equation (2.8) now becomes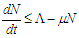 | (2.9) |
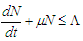 | (2.10) |
The integrating factor for (2.10) is 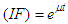 Multiply both sides of (2.10) by
Multiply both sides of (2.10) by 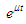 gives
gives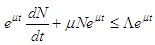 | (2.11) |
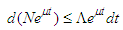 | (2.12) |
Integrating both sides we have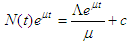 | (2.13) |
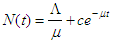 | (2.14) |
Applying the initial condition 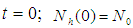
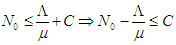 | (2.15) |
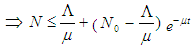 | (2.16) |
Therefore, as 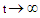 in (2.16) the human population N approaches
in (2.16) the human population N approaches 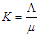
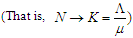 the parameter
the parameter 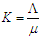 is called the carrying capacity.Hence all feasible solution set of the human population of the model equations (2.1) to (2.6) enter the region
is called the carrying capacity.Hence all feasible solution set of the human population of the model equations (2.1) to (2.6) enter the region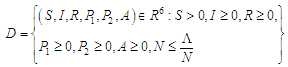 Therefore, the region D is positively-invariant (that is the solution is positive for all times, (t) and equations (2.1) to (2.6) are epidemiologically meaningful and mathematically well-posed in the domain D. Hence in this model it is sufficient to consider the dynamics of flow generated by the model (2.1) to (2.6). In addition, the existence, uniqueness, and continuation of results hold for the system.
Therefore, the region D is positively-invariant (that is the solution is positive for all times, (t) and equations (2.1) to (2.6) are epidemiologically meaningful and mathematically well-posed in the domain D. Hence in this model it is sufficient to consider the dynamics of flow generated by the model (2.1) to (2.6). In addition, the existence, uniqueness, and continuation of results hold for the system.
2.3. Positivity of Solutions
Lemma 2.1 Let the initial data be 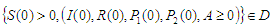 Then the solution set
Then the solution set 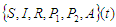 of the system of equations (2.1) to (2.6) is positive for all
of the system of equations (2.1) to (2.6) is positive for all 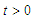 ProofFrom the first equation (2.6), we have
ProofFrom the first equation (2.6), we have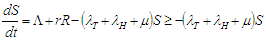 | (2.17) |
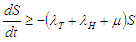 | (2.18) |
Separating the variables and integrating both sides we have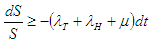 | (2.19) |
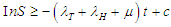 | (2.20) |
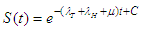 | (2.21) |
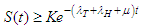 Where
Where 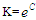 Using the initial condition
Using the initial condition 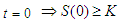 Therefore,
Therefore, 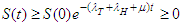 From equation (3.2)
From equation (3.2)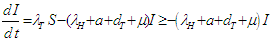 | (2.22) |
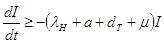 | (2.23) |
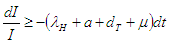 | (2.24) |
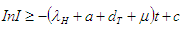 | (2.25) |
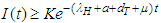 | (2.26) |
Applying the initial condition 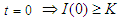 Therefore,
Therefore, 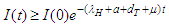 | (2.27) |
Similarly, it can be verified that the rest of the equations are positive for all 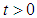 since
since 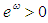 for all
for all 
2.4. Equilibrium States
2.4.1. The Disease Free Equilibrium State of the Model
The equilibrium state with the absence of infection is known as Disease Free Equilibrium or Zero Equilibrium. Therefore the disease-free equilibrium state of the model is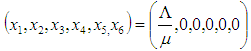
2.4.2. The Endemic Equilibrium State of the Model
The equilibrium state of the model is;
2.5. Basic Reproduction Number R0
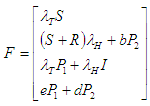 | (2.28) |
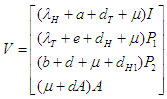 | (2.29) |
the next generation matrix 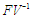 is given by
is given by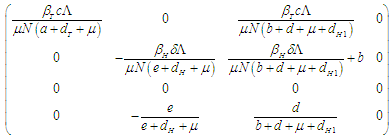 | (2.30) |
Therefore, the basic reproduction number 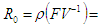 spectra radius of
spectra radius of 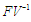
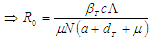 | (2.31) |
3. Stability Analysis of the Model
3.1. Stability Analysis of Disease Free Equilibrium (DFE)
Jacobean matrix of the system of equations at disease-free equilibrium is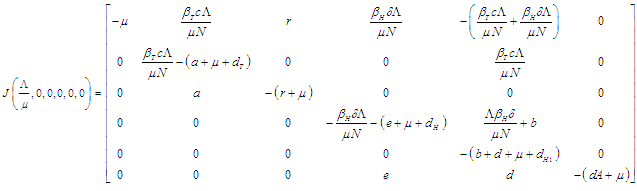 The characteristic equation is
The characteristic equation is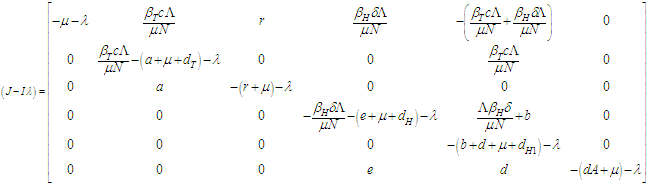 Therefore,
Therefore,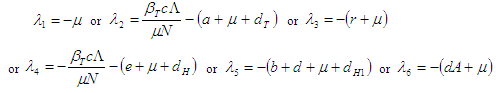 | (3.1) |
From (3.1)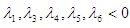 and
and 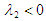 if and only if
if and only if 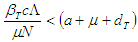 and
and 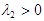 if and only if
if and only if 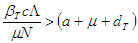 Hence, the DFE is stable if
Hence, the DFE is stable if 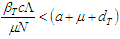 and otherwise unstable.
and otherwise unstable.
3.2. Stability Analysis of Endemic Equilibrium State (EE)
The characteristic equation is obtained from the Jacobi a determinant with the eigenvalues λ  | (3.2) |
Where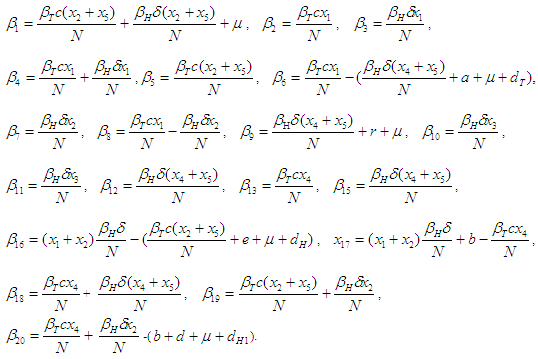 Next we shall apply the result of Bellman and Cooke’s (1963) to (3.2) to establish the stability or otherwise of the model we have;
Next we shall apply the result of Bellman and Cooke’s (1963) to (3.2) to establish the stability or otherwise of the model we have; | (3.3) |
 | (3.4) |
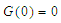 | (3.5) |
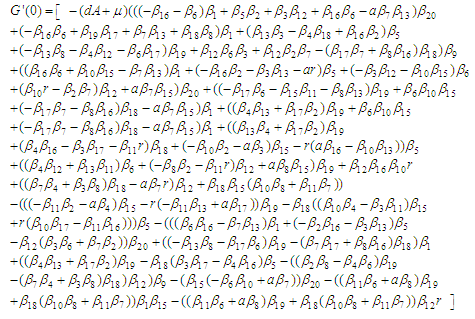 | (3.6) |
Since 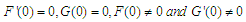
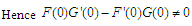 | (3.7) |
Therefore, the non –zero equilibrium state is stable.
4. Conclusions
In this study, we developed and analyzed a mathematical model of HIV/TB co infection. The model subdivides the human population into six compartments namely; Susceptible TB individuals S, TB-infectious individuals I, TB-recovered individuals R, HIV-infected individuals 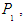 co-infected individuals
co-infected individuals 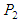 and individuals with full blown AIDS A. The model solution was found to be positive (establishing the fact that human population cannot be negative) for all time
and individuals with full blown AIDS A. The model solution was found to be positive (establishing the fact that human population cannot be negative) for all time 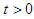 provided that the initial data set is positive.The stability analysis of the Disease Free Equilibrium State (DFE) of the model shows that it will be stable if
provided that the initial data set is positive.The stability analysis of the Disease Free Equilibrium State (DFE) of the model shows that it will be stable if 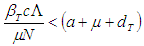 that is the population is sustainable. The analysis of the Endemic Equilibrium State (EES) shows that it is stable. This is in conformity with the real life scenario. That is, whenever HIV is present, the patient may likely be infected with TB if proper and timely care is not given. Also early detection of HIV and TB cases and provision of early treatment can help to control the disease.
that is the population is sustainable. The analysis of the Endemic Equilibrium State (EES) shows that it is stable. This is in conformity with the real life scenario. That is, whenever HIV is present, the patient may likely be infected with TB if proper and timely care is not given. Also early detection of HIV and TB cases and provision of early treatment can help to control the disease.
References
| [1] | Bellman, R., and Cooke, K (1963). Differential Equations. Academic Press, London. PP 11-45. |
| [2] | Bolarin, G. (2012), A Mathematical model of Complacency in HIV/AIDS Scenario: Sex-Structure Approach, Leaonardo Journal of Sciences Issue 21, P.1-12. |
| [3] | Bowong, S., and Tewa, J.J (2010), Global analysis of a dynamical model for transmission of TB with a general content. |
| [4] | Christiana, J.S., and Delfim F.M (2015). ATB-HIV/AIDS co-infection model and optimal control treatment. Series A, ISSN 1078-0947 (print), ISSN 1553-5231 (online). |
| [5] | Deeks, S.G., Lewin S.R., Havlir D.V (2013). The end of AIDS: HIV infection as a chronic disease. The Lancet, Vol. 382, Issue 9903, 1525{1533}. |
| [6] | Funke, J.D., (2013), Mathematical Epidemiology of HIV/AIDS and Tuberculosis Co-infection. |
| [7] | Joyce, K.N., (2015), Mathematical Modeling of Tuberculosis as an Opportunistic Respiratory Co-Infection in HIV/AIDS in the Presence of Protection. Applied Mathematcal Sciences, Vol. 9, 2015, no. 105, 5215 – 5233. |
| [8] | Kendal, M.A., and Havlir, D (2011), Timing of antiretroviral therapy and TB. Analysis of a dynamical model for transmission of tuberculosis with a general content. |
| [9] | Mayer, K (2010), “Synergistic Pandemics: Confronting the Global HIV and Tuberculosis Epidemics” Clinical infectious Diseases, 2010, Volume 50, Supplement 3. |
| [10] | Mandell, G. L., Bennett, J. E., Raphael, D. (2010), Mandell, Douglas, and Bennett's principles and practice of infectious diseases (7th Ed.). Philadelphia, PA: Churchill Livingstone/ Elsevier. |
| [11] | Nigeria TB Fact Sheet, 2012. |
| [12] | Shah, N.H., and Jyota, G (2013), “Modeling of HIV-TB co infection Transmission Dynamics”. American Journal of Epidemiological and Infection Disease 2.1, pp 1-7. |
| [13] | Roeger, W.L., Zhilan, F., and Carlos C.C (2009). Modeling TB and HIV Co-infections. Mathematical Biosciences and Engineering Volume 6, Number 4. Doi:10.3934/mbe.2009.6.815 pp.815-837. |
| [14] | World Health Organization (2011).The Global Plan to Stop TB”, WHO Geneva, 2011. |
| [15] | World Health Organization (2015). Policy on collaborative TB/HIV activities” WHO. |
| [16] | AID gov. https://www.aids.gov/hiv-aids-basics/. Retrieved 12/31/2015 |



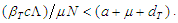

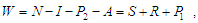 is the active population.To represent this mathematically, we have the following system of differential equations:
is the active population.To represent this mathematically, we have the following system of differential equations: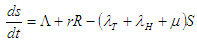
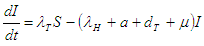
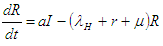
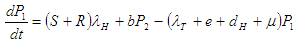
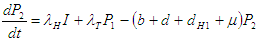
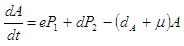
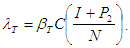 The force of infection
The force of infection 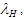 associated with HIV infection is
associated with HIV infection is 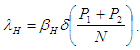
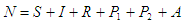
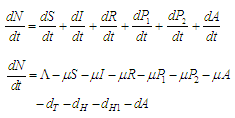
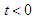 if they enter the invariant region D.ProofLet
if they enter the invariant region D.ProofLet 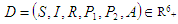 be any solution of the system of equations (2.1) to (2.6) with non-zero initial conditions.Assuming there is no disease equation (2.8) now becomes
be any solution of the system of equations (2.1) to (2.6) with non-zero initial conditions.Assuming there is no disease equation (2.8) now becomes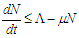
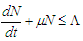
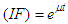 Multiply both sides of (2.10) by
Multiply both sides of (2.10) by 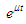 gives
gives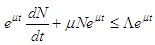
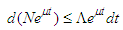
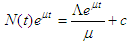
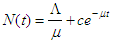
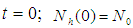
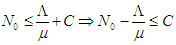
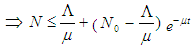
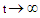 in (2.16) the human population N approaches
in (2.16) the human population N approaches 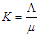
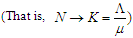 the parameter
the parameter 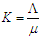 is called the carrying capacity.Hence all feasible solution set of the human population of the model equations (2.1) to (2.6) enter the region
is called the carrying capacity.Hence all feasible solution set of the human population of the model equations (2.1) to (2.6) enter the region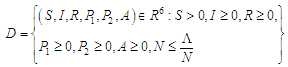 Therefore, the region D is positively-invariant (that is the solution is positive for all times, (t) and equations (2.1) to (2.6) are epidemiologically meaningful and mathematically well-posed in the domain D. Hence in this model it is sufficient to consider the dynamics of flow generated by the model (2.1) to (2.6). In addition, the existence, uniqueness, and continuation of results hold for the system.
Therefore, the region D is positively-invariant (that is the solution is positive for all times, (t) and equations (2.1) to (2.6) are epidemiologically meaningful and mathematically well-posed in the domain D. Hence in this model it is sufficient to consider the dynamics of flow generated by the model (2.1) to (2.6). In addition, the existence, uniqueness, and continuation of results hold for the system. 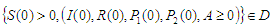 Then the solution set
Then the solution set 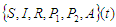 of the system of equations (2.1) to (2.6) is positive for all
of the system of equations (2.1) to (2.6) is positive for all 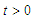 ProofFrom the first equation (2.6), we have
ProofFrom the first equation (2.6), we have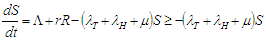
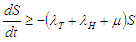
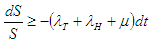
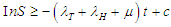
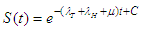
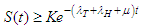 Where
Where 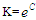 Using the initial condition
Using the initial condition 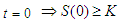 Therefore,
Therefore, 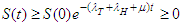 From equation (3.2)
From equation (3.2)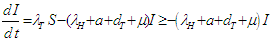
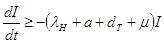
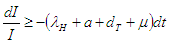
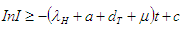
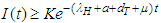
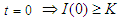 Therefore,
Therefore, 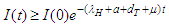
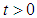 since
since 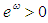 for all
for all 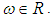
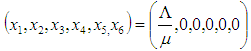

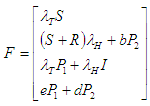
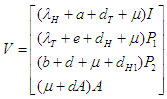
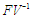 is given by
is given by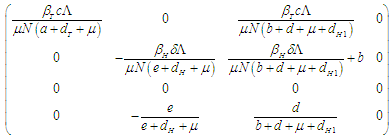
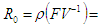 spectra radius of
spectra radius of 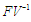
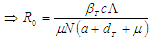
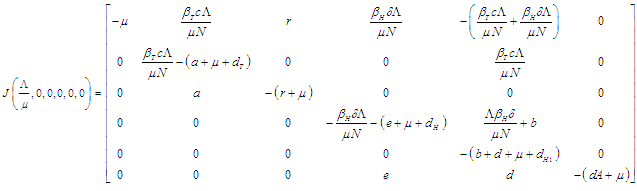 The characteristic equation is
The characteristic equation is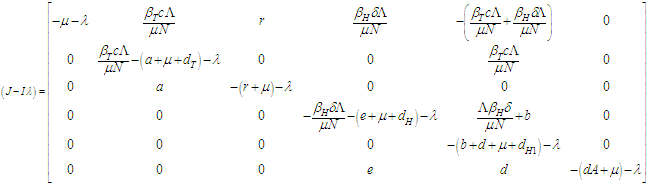 Therefore,
Therefore,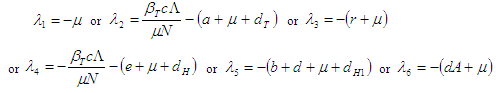
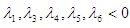 and
and 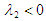 if and only if
if and only if 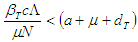 and
and 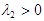 if and only if
if and only if 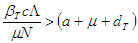 Hence, the DFE is stable if
Hence, the DFE is stable if 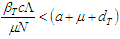 and otherwise unstable.
and otherwise unstable.
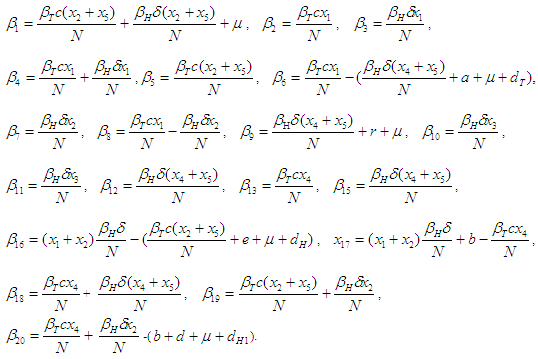 Next we shall apply the result of Bellman and Cooke’s (1963) to (3.2) to establish the stability or otherwise of the model we have;
Next we shall apply the result of Bellman and Cooke’s (1963) to (3.2) to establish the stability or otherwise of the model we have;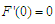
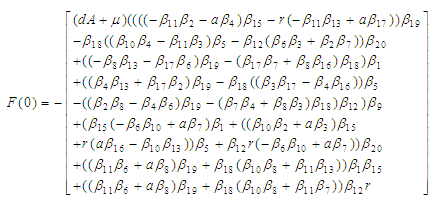
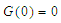
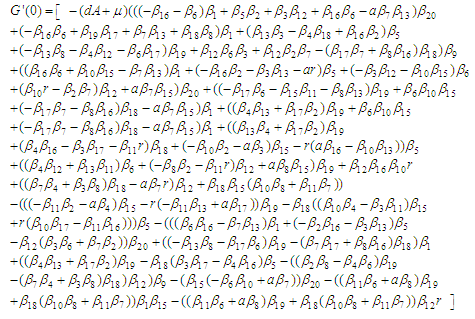
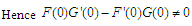
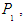 co-infected individuals
co-infected individuals 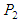 and individuals with full blown AIDS A. The model solution was found to be positive (establishing the fact that human population cannot be negative) for all time
and individuals with full blown AIDS A. The model solution was found to be positive (establishing the fact that human population cannot be negative) for all time 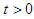 provided that the initial data set is positive.The stability analysis of the Disease Free Equilibrium State (DFE) of the model shows that it will be stable if
provided that the initial data set is positive.The stability analysis of the Disease Free Equilibrium State (DFE) of the model shows that it will be stable if 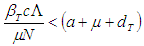 that is the population is sustainable. The analysis of the Endemic Equilibrium State (EES) shows that it is stable. This is in conformity with the real life scenario. That is, whenever HIV is present, the patient may likely be infected with TB if proper and timely care is not given. Also early detection of HIV and TB cases and provision of early treatment can help to control the disease.
that is the population is sustainable. The analysis of the Endemic Equilibrium State (EES) shows that it is stable. This is in conformity with the real life scenario. That is, whenever HIV is present, the patient may likely be infected with TB if proper and timely care is not given. Also early detection of HIV and TB cases and provision of early treatment can help to control the disease.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML