1. Introduction

Human Immunodeficiency Virus (HIV) is a virus that gradually attacks the immune system, which is our body’s natural defense against illness. If a person becomes infected with HIV, they will find it harder to fight off infections and diseases. The virus destroys a type of white blood cell called a T-helper cell and makes copies of itself inside them. T-helper cells are also referred to as CD4 cells [1, 4, 7].

The first cases were reported in 1981 and today there are approximately 36.9 million people currently living with HIV and tens of millions of people have died of AIDS-related causes since the beginning of the epidemic [2, 3, 5]. While new cases have been reported in all regions of the world, approximately 70% are in sub-Saharan Africa [9]. Most people living with HIV or at risk for HIV do not have access to prevention, care, and treatment, and there is still no cure [15, 17]. HIV primarily affects those in their most productive years; about 38% of new infections are among those under age 25 [6, 8].

HIV is found in the blood, sexual and bodily fluids of an infected person. The most common form of transmission are unsafe sex, unsafe blood transfusion, transmission from mother to child, intravenous drug use with contaminated needles and other blood related modes like bleeding wounds.

It targets and infects white blood cells known as CD4+ T-cells which are part of the immune system. CD4+ T-cells are helper cells produced from precursors in bone marrow and thymus. When a person has chronic HIV infection, it causes gradual depletion of the CD+4 T-cell pool In a normal human being the level of CD+4 T-cells in the peripheral blood is regulated at a level between 800mm^-3 to 1200mm^-3 when the CD+4 T-cell count falls below 200mm^-3, a person becomes vulnerable to opportunistic infections. CD+4 T-cells are a primary indicator used to measure progression of HIV infection in an HIV infected person [10, 11, 12].

Despite these challenges, new global efforts have been mounted to address the epidemic, particularly in the last decade, and there are signs that the epidemic may be changing course. The number of people newly infected with HIV and the number of AIDS-related deaths have declined, contributing to the stabilization of the epidemic. In addition, the number of people with HIV receiving treatment has increased to 15.8 million as of June 2015, a 2.2 million increase since June 2014. Young people, ages 15-24, account for approximately 30% of new HIV infections (among those 15 and over) [9, 13, 16].

Malaria is an infectious disease caused by Plasmodium parasites and transmitted between humans through bites of female Anopheles mosquitoes. Malaria was first discovered centuries ago by the Chinese in 2700 BC [6]. However it was in the 1800’s when Ross made his ground breaking discoveries that led to our understanding of the mechanics behind malaria infections. About 3.2 billion people – nearly half of the world's population – are at risk of malaria. In 2015, there were roughly 214 million malaria cases and an estimated 438000 malaria deaths. Increased prevention and control measures have led to a 60% reduction in malaria mortality rates globally since 2000. Sub-Saharan Africa continues to carry a disproportionately high share of the global malaria burden. In 2015, the region was home to 89% of malaria cases and 91% of malaria deaths [8, 14].

The most common first symptoms of malaria are similar to those of Flu. The patient may experience headache, aching muscles, stomach ache and weak or lack of energy. After a day or so the body temperature may rise (up to 40°C) and the patient may have fever, shivers, severe headache, diarrhea, loss of appetite, nausea, vomiting, back pain and increased sweating. The individuals most vulnerable to malaria are children under the age of 5 years. This is attributed to their weaker immunity. Aside from children, pregnant women are also heavily affected, with resultant effects on maternal health and birth outcomes.

Treatment of malaria depends on many factors including disease severity, the species of malaria parasite causing the infection and the part of the world in which the infection was acquired. The latter 2 characteristics help determine the probability that the organism is resistant to certain anti-malarial drugs. Additional factors such as age, weight, and pregnancy status may limit the available options for malaria treatment [10].

Malaria and human immunodeficiency virus (HIV) are the most deadly and important global health problems of our time. Malaria accounts for more than a million deaths each year, of which about 90% occur in tropical Africa, where malaria is the leading cause of mortality in children below five years [26]. Sub-Saharan Africa is also home to more than 29 million people living with HIV/AIDS. Both Malaria and HIV are considered as diseases of poverty, since they hinder sustainable development and contribute to poverty by taking a great toll on the young productive generation who would otherwise enter the workforce and contribute to the nation’s economy. The global distribution of Malaria and HIV is the same, with the majority of those affected living in sub-Saharan Africa, the Indian subcontinent, and Southeast Asia. Owing to the overlap of their geographic distribution and resultant rates of co-infection, interactions between the two diseases pose major public health problems [8].

This study was carried out from October to November 2013 in Owena, Idanre Local Government Area and State Hospital Akure, Ondo State. A total of 150 people of different age groups and sexes were screened for malaria and co-infection with HIV. In Owena and State hospital, 88 and 62 blood samples were examined respectively for the presence of malaria using thick and thin smear, and also for the presence of Human Immunodeficiency Virus (HIV) using Abbott Determine kit and Stat Pak kit. A standardized questionnaire was used to obtain information’s from each person. Such information is those relating the infection rate with age, sex and state of origin, place of residence [19].

2. Formulation of Model

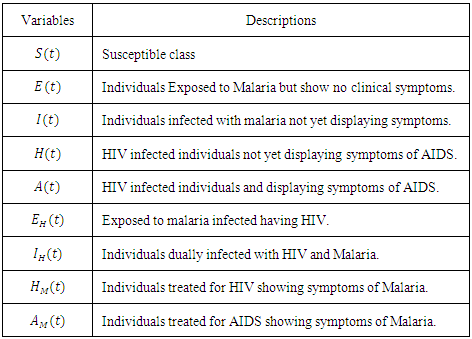
In modelling the total human population at any time t, denoted by 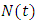is subdivided into sub-population namely, Susceptible 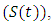who are not yet infected either by HIV or malaria, exposed to Malaria but show no clinical symptoms of the disease 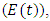exposed to malaria infected having HIV 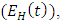individuals infected with malaria not yet displaying symptoms 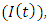HIV infected individuals not yet displaying symptoms of AIDS 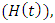HIV infected individuals yet displaying symptoms of AIDS 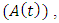individuals dually infected with HIV and malaria 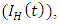individuals treated for HIV showing symptoms of malaria 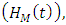individuals treated for AIDS showing symptoms of malaria

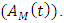Thus we have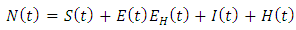

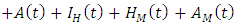The susceptible population is increased by the recruitment of individuals (assumed susceptible) into the population at a rate

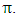Susceptible individuals acquire Malaria infection, following effective contact with the people infected with Malaria only (i.e. those in the E, 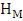and 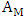classes) at a rat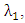e where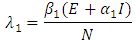

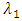is the force of infection for malaria. Here 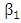is the transmission rate for Malaria and 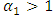accounts for the assumed reduction of infectivity of infectious individuals in the exposed class and known as the modification parameter.

Similarly, the susceptible individuals acquire HIV from with HIV at a rate 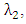where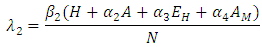

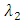is the force of infection for HIV. Here 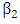is the transmission rate for HIV and 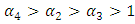accounts for the assumed reduction of infectivity of infectious individuals in the exposed class and known as the modification parameter.

In the susceptible class, population is entering into this class at a constant rate

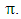In the malaria exposed class 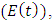individuals entering into this class from susceptible class 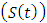at a rate 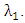Also individuals entering into the HIV class 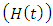from susceptible class 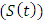at a rate

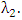In the malaria infected class 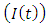, individual progresses to Malaria infected class 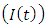from the Malaria exposed class 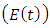at a rate 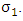In this class, let 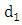denotes the death rate due to the disease. In AIDS class 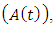individual is advancing to AIDS class 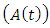from HIV infected class 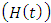at a rate 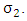In this class, let 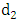denotes the death rate due to the disease.

In the exposed to malaria infected having HIV class 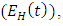individuals forward movement rate to malaria infected having HIV class

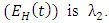Dually infected with HIV and malaria class is denoted by 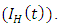Now the individuals progress to dually infected with HIV and malaria class 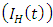from the exposed to malaria infected having HIV class 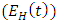at a rate 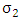. Also individually progress to this class from Malaria infected class 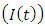. In this class, let 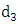denotes the death rate due to the disease.

HIV class having Malaria is denoted by 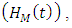individual’s forward movement to HIV class having Malaria 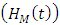from the HIV class 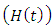at a rate

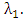AIDS class having Malaria 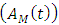, individuals advancement to AIDS class having Malaria 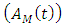from the HIV class having Malaria 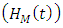at a rate 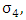also individually progress to this class from AIDS class 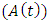at a rate 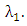In this class, let 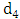denotes the death rate due to the disease.

In Malaria infected class 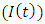, AIDS class 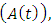dually infected with HIV and malaria class 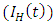and AIDS class having Malaria 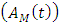, the disease induced death rates are denoted by 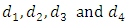respectively. Further, natural mortality occurs in all classes is denoted by

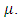Combining all the aforementioned assumption and definitions, the model becomes:

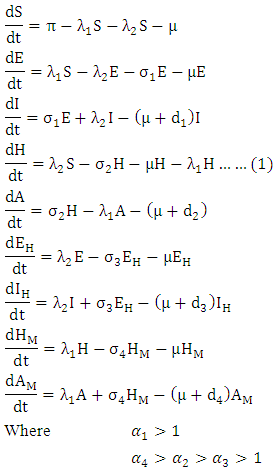Schematically this can be shown as,

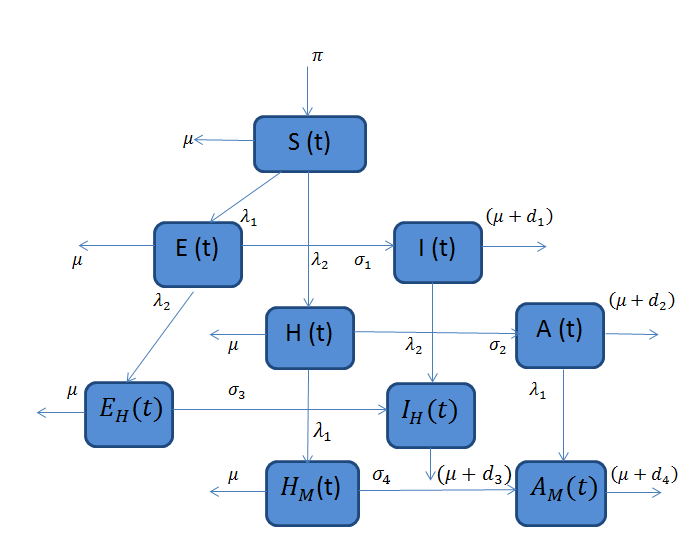Figure 1. Diagram of the model

3. Positivity and Boundedness of Solution

Model (1) describes the co-infection of Malaria and HIV diseases and therefore it can be shown that the associated state variables are non-negative for all time 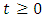and that the solutions of the model (1) with positive initial data remains positive for all time 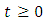[15]. We assume the associated parameters are non-negative all time 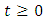all feasible solutions are uniformly bounded in a proper subset

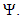Theorem: Solutions of the model (1) are contained in a region where 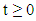[15].

Proof: To show that all feasible solutions are uniformly-bounded in a proper subs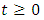et . Let 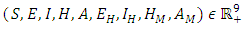be any solution with non-negative initial conditions. From the theorem on differential inequality if t follows that,

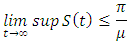Taking the time derivative of N along a solution path of the model (1) gives

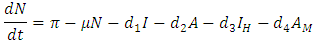Then,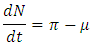

From the theorem on differential inequality it follows that,

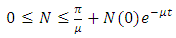Where, 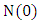represents the value of (1) evaluated at the initial values of the respective variables. Thus as 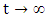we have

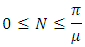It follows that 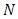is bounded and all the feasible solutions of the model (1) starting in the region 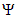for all approaches, enter or stay in the region, where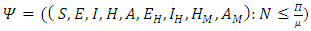

Thus Ψ is positively invariant under the flow induced by (1). Existence, uniqueness and continuation results also hold for the model (1) in 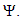Hence model (1) is well-posed mathematically and epidemiologically and it is sufficient to consider its solutions in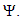

4. Disease-free Equilibrium Point

Disease-free equilibrium (DFE) points of a disease model are its steady-state solutions in the absence of infection or disease. We denote this point by 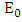and define the “diseased” classes that are either exposed or infectious. Then can construct the following two lemmas.

Lemma: For all equilibrium points on 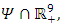for which 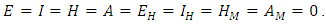Then the positive DFE for the model (1) is

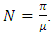Lemma: The model (1) has exactly one DFE and the DFE point is

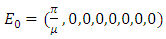Proof: The proof of the lemma requires that we show that the DFE is the only equilibrium point of (1) on 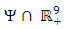Substituting 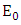into (1) shows all derivatives equal to zero, hence DFE is an equilibrium point. From above lemma, the only equilibrium point for N is 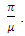Thus the only equilibrium point for 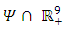is DFE.

5. Local Stability of the Disease-free Equilibrium

The global stability of the model (1) is highly dependent on the basic reproduction number which is denoted by 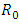[3]. The basic reproduction number is defined as the expected number of secondary infections produced by an index case in a completely susceptible population. The associated nonnegative matrix F, for the new infection terms, and the non-singular M-matrix, V, for the remaining transfer terms are given respectively, by

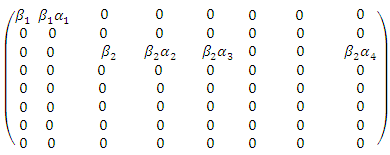and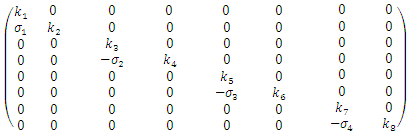

Where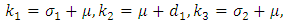

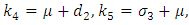
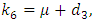
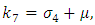
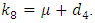The basic reproduction number 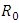is the spectral radius of the 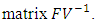By using Maple the eigenvalues of th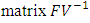e are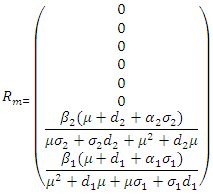

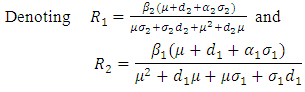we have,

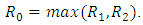Thus we have the following lemma

Lemma: The disease-free equilibrium 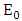of the model (1) is locally asymptotically stable whenever 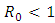and unstable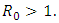

6. Global Stability of the Disease-free Equilibrium

The global asymptotically stability (GAS) of the disease-free state of the model is investigated using the theorem by Castillo-Chavez. We rewrite the model as:

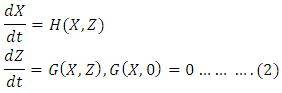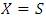Where and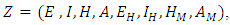

with the components of 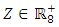denoting the infected population.

The disease free equilibrium is now denoted as:

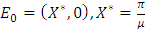The condition must be met to guarantee a local asymptotic stability

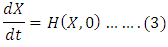Here, 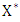is globally asymptotically stable (GAS)

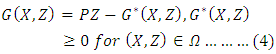Where 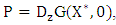is an M-matrix (the off-diagonal elements of P are non-negative) and 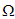is the region where the model makes biological sense. If the system (3) satisfies the conditions of (4) then the theorem below holds:

Theorem: The fixed point 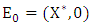is a globally asymptotically stable equilibrium of the system (3) provided that 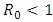and the assumptions in (4) are satisfied.

Proof: Form the model system (1) and (4), we have

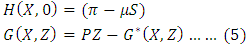Where 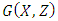is as follows:

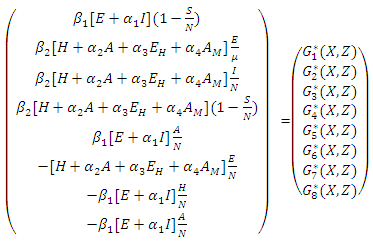Here 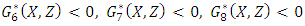and so the conditions are not met. So 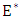may not be globally asymptotically stable when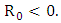

7. Endemic Equilibrium of the Model

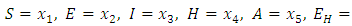
A disease is endemic in a population if it persists in a population. The endemic equilibrium of the model is studied using the Central Manifold Theorem [1]. To apply this theorem we make the following change of variables. Let 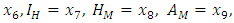so that

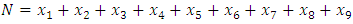The model (1) can be rewritten in the form:

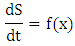Where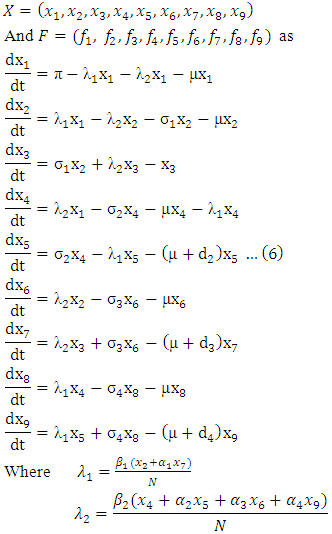

The Jacobian of the system (6) is

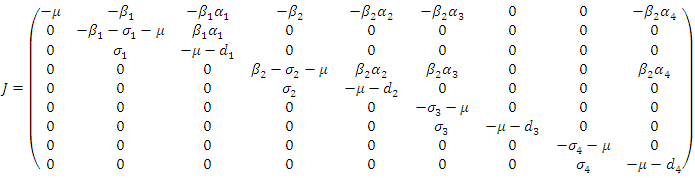To analyze the dynamics of (6), we compute the eigenvalues of the Jacobean of (6) at the disease free equilibrium (DFE). It can be shown that this Jacobean has a right eigenvector given by:

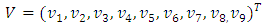Where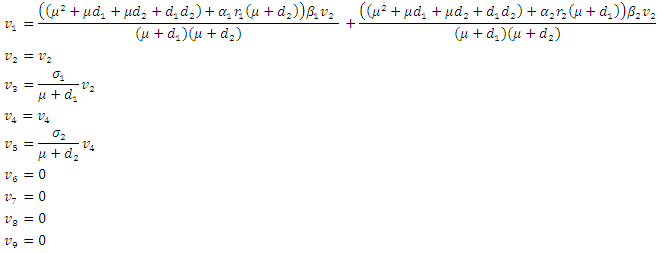

And the left eigenvectors are given by

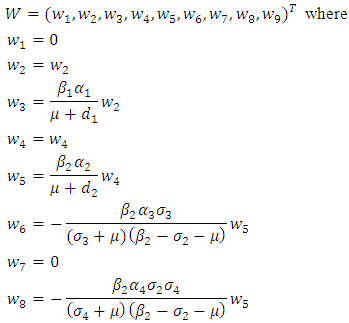Now using (6) we have

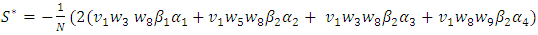And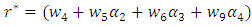

Clearly we can see that

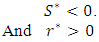Thus we have established the following theorem:

Theorem. The model (1) has a unique endemic equilibrium which is locally asymptotically stable when 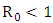and unstable when 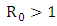[16].

8. Numerical Simulations and Discussions

The parameters and their values that are used the model are listed below.

Table 1. Description of parameters of model

Table 2. The value of the parameters of the model

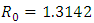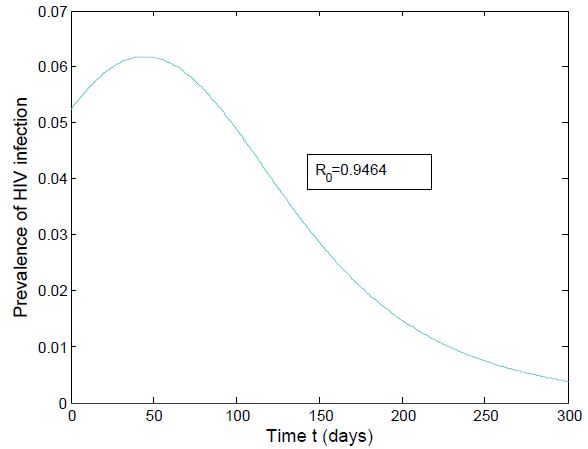
Figure (2) shows that the infected population is increasing when the basic reproduction number which is bigger than 1 and figure (3) shows that the infected population is decreasing when 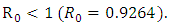Figure (4) (prevalence of HIV infection) indicates that the number of total infected population increases whenever the basic reproduction number 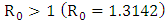and the figure (5) shows that the prevalence of HIV infection decreases when 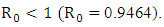Figure (6) and (7) (HIV and Malaria co-infection) both indicate respectively that when the basic reproduction number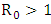 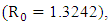the number of total infected population increases and when 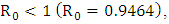the number of total infected population decreases.

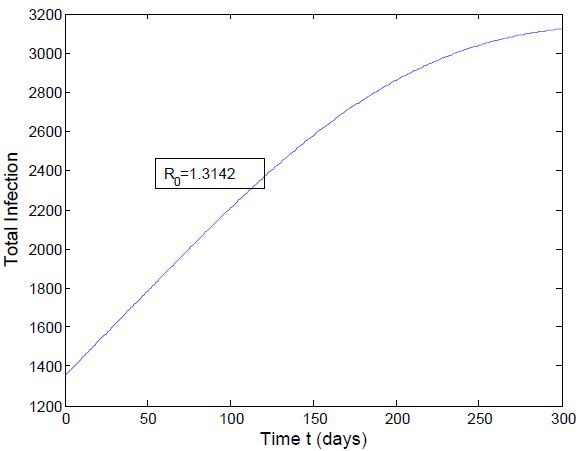Figure 2. Total infection when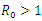

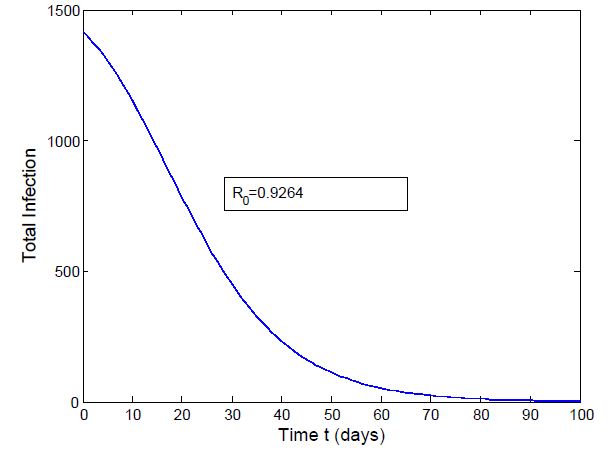Figure 3. Total Infection when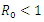

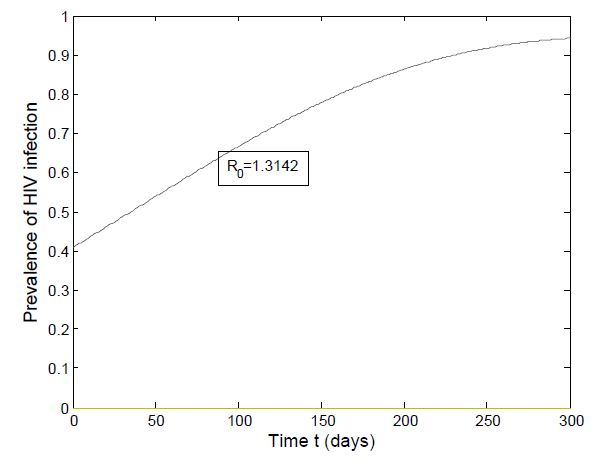Figure 4. Prevalence of HIV when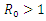

Figure 5. Prevalence of HIV when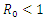

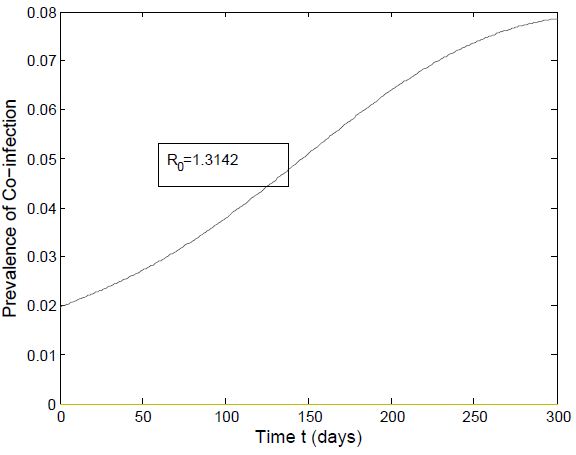Figure 6. Prevalence of Co-infection when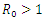

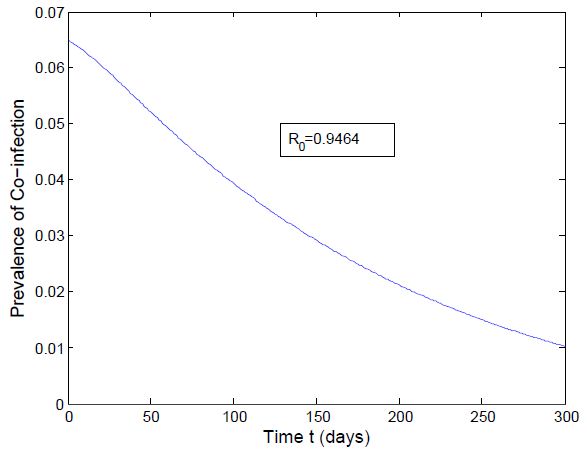Figure 7. Prevalence of Co-infection when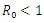

9. Conclusions

HIV and malaria affect millions of people across overlapping geographic distributions. The risk of transmission of both diseases can be increased because of co-infection. Here we have formulated a deterministic mathematical model for the co-infection of HIV/AIDS and malaria in order to assess their synergic relationship. Positivity and boundness of solutions are analyzed quantitatively. Sensitivity indices of the basic reproductive number 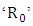to the parameters in the model is calculated. Comprehensive mathematical techniques are used to analyze the model steady states. It is found that using the next generation matrices, the disease free equilibrium point is locally asymptotically stable when the reproduction number is less than unity and unstable when reproduction number is greater than unity. Centre manifold theory is used to show that the HIV/AIDS-malaria co-infection model`s endemic equilibrium are locally asymptotically stable when the associated reproduction numbers are less than unity. In summary, the main findings of this paper, if reduction in sexual activity of individuals with malaria symptoms decreases the number of new cases of HIV and the mixed HIV-malaria infection and also protecting HIV infective from mosquito bites.