-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2016; 6(3): 41-47
doi:10.5923/j.am.20160603.01

Effect of Change of Origin of Variables on Ratio Estimator of Population Mean
Sarbjit S. Brar1, Jasleen Kaur2
1Department of Statistics, Punjabi University, Patiala, India
2Department of Mathematics, Punjabi University, Patiala, India
Correspondence to: Sarbjit S. Brar, Department of Statistics, Punjabi University, Patiala, India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In last two decades, a number of modified ratio estimators for population mean have been developed by using the known information of auxiliary variable under different sampling strategies. The functional form of these estimators is, mathematically, not justifiable because these estimators have been obtained by using transformation of auxiliary variable by adding a unit free constant or quantities with different units. But these modified estimators are more efficient than the usual ratio estimator of population mean. So, it is clear that there is some effect of change of origin of auxiliary variable on the usual ratio estimator. In the present paper, we have discussed the effect of change of origin of auxiliary as well as study variable on ratio estimator of population mean and have also obtained the optimum transformations in the cases of over estimation and under estimation. Also, the conditions for validity of approximate results of the ratio estimator have been obtained which can be easily verified in practical situations. Further, we have carried out a simulation study to verify the theoretical results.
Keywords: Efficiency, Ratio Estimation, Simple Random Sampling, Transformation
Cite this paper: Sarbjit S. Brar, Jasleen Kaur, Effect of Change of Origin of Variables on Ratio Estimator of Population Mean, Applied Mathematics, Vol. 6 No. 3, 2016, pp. 41-47. doi: 10.5923/j.am.20160603.01.
Article Outline
1. Introduction
- [1] initiated the use of auxiliary information to estimate population mean in sample survey. He proposed the ratio estimator
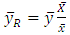 to estimate population mean
to estimate population mean 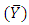 which can also be used to estimate population total
which can also be used to estimate population total 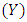 where
where 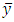 and
and 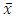 denote the sample means of study and auxiliary variables respectively and
denote the sample means of study and auxiliary variables respectively and 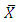 denotes the population mean of auxiliary variable. This ratio estimator is more efficient than mean per unit estimator if
denotes the population mean of auxiliary variable. This ratio estimator is more efficient than mean per unit estimator if 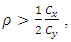 where
where 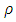 is the correlation coefficient between the auxiliary
is the correlation coefficient between the auxiliary 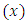 and the study
and the study 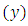 variables;
variables; 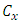 and
and 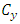 are coefficients of variation for auxiliary and study variables respectively.Further, on the same pattern, [2] proposed a product estimator
are coefficients of variation for auxiliary and study variables respectively.Further, on the same pattern, [2] proposed a product estimator 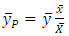 for
for 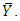 The product estimator is more efficient than mean per unit estimator if
The product estimator is more efficient than mean per unit estimator if 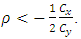 Using the power transformation, [3] proposed a new estimator
Using the power transformation, [3] proposed a new estimator 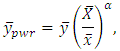 to estimate
to estimate 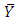 and he found the optimum value of
and he found the optimum value of 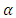 for which the MSE of
for which the MSE of 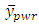 is minimum. After this, many statisticians proposed different kinds of estimators using auxiliary information. But [4] proposed a modified ratio estimator for
is minimum. After this, many statisticians proposed different kinds of estimators using auxiliary information. But [4] proposed a modified ratio estimator for 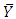 using the additional known information of coefficient of variation of auxiliary variable as:
using the additional known information of coefficient of variation of auxiliary variable as: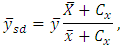 Thereafter, it became a trend to propose modified ratio estimators for
Thereafter, it became a trend to propose modified ratio estimators for 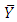 by using additional known information of auxiliary variable. Some related examples are as follows:[5]
by using additional known information of auxiliary variable. Some related examples are as follows:[5]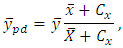 [6]
[6]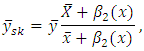 where
where 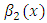 is coefficient of kurtosis of auxiliary variable.[7]
is coefficient of kurtosis of auxiliary variable.[7] 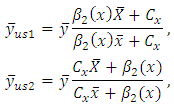 [8]
[8]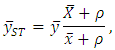 [9]
[9]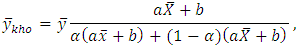 where
where 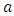 and
and 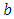 are real numbers or some known parameters of auxiliary variable.[10]
are real numbers or some known parameters of auxiliary variable.[10]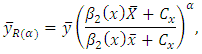 where
where 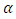 is some real constant.[11]
is some real constant.[11]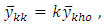 where
where 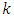 is some real constant.[12]
is some real constant.[12] 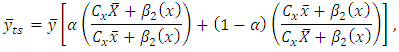 [13]
[13]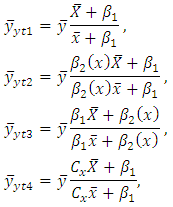 where
where 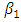 is the coefficient of skewness of auxiliary variable.All the above estimators are more efficient than the classical ratio estimator but in these estimators, researchers have added a pure number in the quantity which possesses a unit which is mathematically not possible. For example, the mean of auxiliary variable
is the coefficient of skewness of auxiliary variable.All the above estimators are more efficient than the classical ratio estimator but in these estimators, researchers have added a pure number in the quantity which possesses a unit which is mathematically not possible. For example, the mean of auxiliary variable 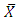 is measured in centimeters and the coefficient of variation is always a pure number, still [4] and [5] added these two quantities. The main question which arises here is "Can we add these two quantities?" This question was first raised by [14]. If the answer is in the negative, then the question arises about the authenticity of the estimators proposed by different researchers using above assumption.The aim of the present paper is to discuss these issues and find out the situation where one can use the classical ratio estimator. In Section-2, the basic conditions for the ratio estimator of population mean have been discussed. The effects of change of origin of variables on ratio estimator of population mean have been presented in Section-3. A detailed discussion about the clarification given by [15] on the transformation of auxiliary variable has been presented in Section-4 and the idea for further study has been proposed in Section-5. In Section-6, a simulation study has been carried out to verify theoretical results. In the last section, the conclusion of the present paper has been drawn.
is measured in centimeters and the coefficient of variation is always a pure number, still [4] and [5] added these two quantities. The main question which arises here is "Can we add these two quantities?" This question was first raised by [14]. If the answer is in the negative, then the question arises about the authenticity of the estimators proposed by different researchers using above assumption.The aim of the present paper is to discuss these issues and find out the situation where one can use the classical ratio estimator. In Section-2, the basic conditions for the ratio estimator of population mean have been discussed. The effects of change of origin of variables on ratio estimator of population mean have been presented in Section-3. A detailed discussion about the clarification given by [15] on the transformation of auxiliary variable has been presented in Section-4 and the idea for further study has been proposed in Section-5. In Section-6, a simulation study has been carried out to verify theoretical results. In the last section, the conclusion of the present paper has been drawn.2. Ratio Estimator
- In all the modified ratio estimators, researchers had changed either origin only or both the origin and scale of auxiliary variable. Due to this change, there is some reduction in bias and MSE of modified ratio estimators as compared to those of the classical ratio estimator. It means that there is some effect of change of origin and scale of auxiliary variable. To understand this reduction of bias and MSE, there is a need to understand the assumptions of classical ratio estimator which are as follows:-1. To obtain the approximate results for ratio estimator, the conditions are
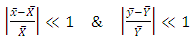 | (1) |
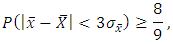 where
where 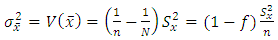 and
and 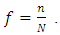 The above inequality shows that
The above inequality shows that 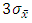 is the upper bound of
is the upper bound of 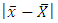 with probability more than
with probability more than 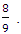 Using this upper bound in (1), we get
Using this upper bound in (1), we get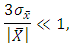 or
or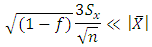 After ignoring the finite population correction, we get
After ignoring the finite population correction, we get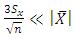 | (2) |
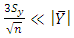 | (3) |
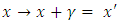 and
and 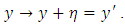 Since the left hand side of these inequalities is independent of change of origin, these transformations affect only the right side. These new variables can further be used in ratio estimation of population mean. In the present paper, we assume that these inequalities are satisfied for variables
Since the left hand side of these inequalities is independent of change of origin, these transformations affect only the right side. These new variables can further be used in ratio estimation of population mean. In the present paper, we assume that these inequalities are satisfied for variables 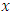 and
and 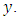 2. Classical ratio estimator of population mean is more efficient than mean per unit estimator provided
2. Classical ratio estimator of population mean is more efficient than mean per unit estimator provided 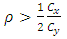 | (4) |
3. Effect of Change of Origin of Variables
- After assuming the conditions given in (1), one can easily obtain the approximate bias and MSE for classical ratio estimator as
 | (5) |
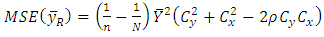 | (6) |
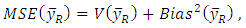 | (7) |
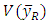 is the minimum value of
is the minimum value of 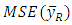 if bias of the estimator become zero.
if bias of the estimator become zero. 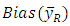 may be positive or negative. Both the cases have been discussed as follows:-
may be positive or negative. Both the cases have been discussed as follows:-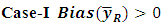 We have from equation (5),
We have from equation (5),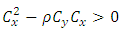 or
or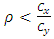 | (8) |
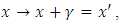 where
where 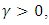 there is reduction in
there is reduction in 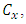 that is
that is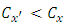 | (9) |
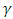 as
as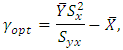 such that
such that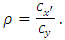 | (10) |
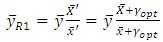 | (11) |
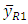 are as
are as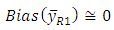 and
and 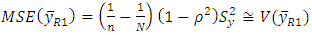 | (12) |
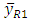 is an approximately unbiased estimator of population mean
is an approximately unbiased estimator of population mean 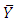 and the estimator
and the estimator 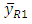 is always more efficient than mean per unit estimator.In practical situations, the value of
is always more efficient than mean per unit estimator.In practical situations, the value of 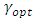 is generally unknown. So one can use the estimated value of
is generally unknown. So one can use the estimated value of 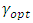 as
as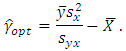
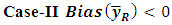 From equation (5), we get
From equation (5), we get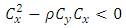 or
or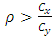 | (13) |
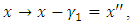 where
where 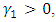 there is increase in
there is increase in 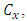 that is
that is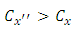 | (14) |
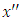 may violate the condition given in (1). So here, we shall use a new transformation
may violate the condition given in (1). So here, we shall use a new transformation 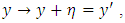 where
where 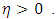 If we compare the coefficients of variation of these variables, we get
If we compare the coefficients of variation of these variables, we get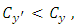 By using the optimum value of
By using the optimum value of 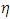 as
as 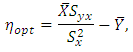 we get
we get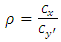 | (15) |
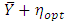 as
as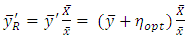 | (16) |
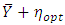 and the approximate variance is same as the variance of
and the approximate variance is same as the variance of 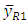 as given in (12).Modified ratio estimator for
as given in (12).Modified ratio estimator for 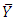 may be defined as
may be defined as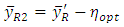 | (17) |
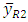 remains unbiased for
remains unbiased for 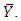 Also the variance of
Also the variance of 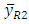 remains same as the variance of
remains same as the variance of 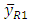 given in (12).The optimum value of
given in (12).The optimum value of 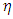 contains some unknown parameters, so one can use the estimated value of
contains some unknown parameters, so one can use the estimated value of 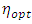 in practical situations as
in practical situations as 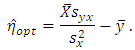 From the above discussion, one concludes that if there is a problem of over estimation during ratio estimation of population mean, then it can be solved by shifting the origin of the auxiliary variable. Similarly, if there is a problem of under estimation, then it can be reduced by shifting the origin of the study variable. Further, one more question arises- "What will happen if we change the origin and scale of the auxiliary variable?" To answer this, we consider the following transformation on auxiliary variable.
From the above discussion, one concludes that if there is a problem of over estimation during ratio estimation of population mean, then it can be solved by shifting the origin of the auxiliary variable. Similarly, if there is a problem of under estimation, then it can be reduced by shifting the origin of the study variable. Further, one more question arises- "What will happen if we change the origin and scale of the auxiliary variable?" To answer this, we consider the following transformation on auxiliary variable.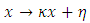 which implies that
which implies that In this case, the modified ratio estimator may be defined as
In this case, the modified ratio estimator may be defined as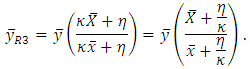 It shows that in ratio estimation, the transformation
It shows that in ratio estimation, the transformation 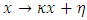 is equivalent to the transformation
is equivalent to the transformation 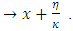 One can modify the ratio estimator
One can modify the ratio estimator 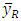 by shifting the origin of auxiliary variable or study variable and this modified estimator is always more beneficial than the existing one. Different modified ratio estimators proposed by the researchers by using the additional known information of auxiliary variable are mathematically not correct. But these estimators perform better than classical ratio estimator due to the change of origin of auxiliary variable; not due to additional known information.
by shifting the origin of auxiliary variable or study variable and this modified estimator is always more beneficial than the existing one. Different modified ratio estimators proposed by the researchers by using the additional known information of auxiliary variable are mathematically not correct. But these estimators perform better than classical ratio estimator due to the change of origin of auxiliary variable; not due to additional known information. 4. Clarification by Singh and Kumar
- [14] and [16] raised a question regarding transformation of auxiliary variables by adding a unit free constant. But [15] try to clarify the same with the help of following three examples:1. “Let
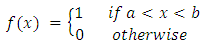 | (18) |
 which is in fact the distance between two points
which is in fact the distance between two points 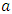 and
and 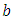 on a real line, say
on a real line, say 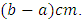 Now, to make
Now, to make 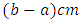 as area, we have to multiply it by
as area, we have to multiply it by 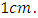 The required area will be:
The required area will be: 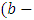
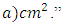 2. “If we integrate speed
2. “If we integrate speed 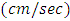 of an object with respect to time, then we get distance in
of an object with respect to time, then we get distance in 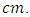 Now distance is not area, as expected after integrating a function, but it is distance in centimeter.”3.
Now distance is not area, as expected after integrating a function, but it is distance in centimeter.”3. 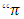 is constant and an irrational number, but has radian as units of measurements.”On the basis of these three examples, they asserted that these kinds of adjustments of units of measurements are common in practice.Our Clarification:First of all, in the above three examples we need to understand whether an adjustment has really been done or not. Let us recall the definition of integration as follows:Let
is constant and an irrational number, but has radian as units of measurements.”On the basis of these three examples, they asserted that these kinds of adjustments of units of measurements are common in practice.Our Clarification:First of all, in the above three examples we need to understand whether an adjustment has really been done or not. Let us recall the definition of integration as follows:Let 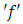 be a bounded real-valued function on
be a bounded real-valued function on 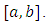 It means that
It means that 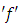 is also bounded on each sub-interval corresponding to each partition
is also bounded on each sub-interval corresponding to each partition 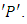 Let
Let 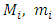 be the least upper bound and greatest lower bound of
be the least upper bound and greatest lower bound of 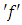 in
in 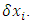 Then there are two sums,
Then there are two sums,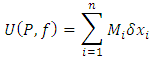 and
and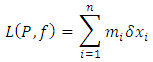 respectively called the upper and lower sums of
respectively called the upper and lower sums of 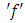 corresponding to the partition
corresponding to the partition 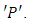 Further, infimum of the set of upper sums is called the upper integral and supremum of the set of lower sums is called the lower integral over
Further, infimum of the set of upper sums is called the upper integral and supremum of the set of lower sums is called the lower integral over 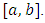 That is
That is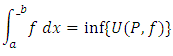 and
and 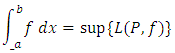 If two integrals are equal, i.e.
If two integrals are equal, i.e.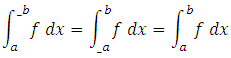 then
then 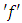 is said to be Riemann integrable or simply integrable over
is said to be Riemann integrable or simply integrable over 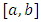 and the common value of these integrals is called the integral of
and the common value of these integrals is called the integral of 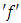 over
over 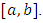 For more details of the concept of integration, see [17].From the above definition, it is clear that The units of integral of
For more details of the concept of integration, see [17].From the above definition, it is clear that The units of integral of 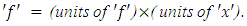 In equation (18), if both
In equation (18), if both 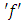 and
and 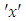 have units in
have units in 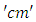 then from the definition, we have
then from the definition, we have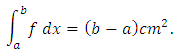 Similarly, when we integrate speed(cm/sec) of an object with respect to time(sec), then we get units of the integral in cm. Further, we know that each individual real number is a constant and
Similarly, when we integrate speed(cm/sec) of an object with respect to time(sec), then we get units of the integral in cm. Further, we know that each individual real number is a constant and 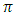 is one of them. The number
is one of them. The number 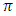 does not possess any units like radian. For example, if height of a person is 72 inches, it does not mean that 72 has inches as units. The units are possessed by variable height but not by 72.From above discussion, it is clear that in all the three examples given by [15], there is no adjustment of units.
does not possess any units like radian. For example, if height of a person is 72 inches, it does not mean that 72 has inches as units. The units are possessed by variable height but not by 72.From above discussion, it is clear that in all the three examples given by [15], there is no adjustment of units. 5. Further Study
- In the last two decades, a number of modified estimators have been developed under various sampling strategies using transformations of auxiliary variables by shifting origin by adding units free constants or quantities with different units. This type of modifications are mathematically not justifiable. So there is a need to find out the actual reasons about what happens when we change the origin under those sampling strategies. Some of the work which has been done using this pattern by different researchers is mentioned in [18-36] and many more.
6. Simulation Study
- A simulation study has been carried out to verify the theoretical results by using software R. Firstly, results have been obtained on the basis of 1,00,000 samples each of size n=3, 5 and 7 from each of normal populations
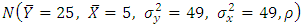 , where
, where 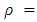
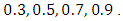 For these populations, auxiliary variable
For these populations, auxiliary variable 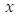 does not satisfy the condition
does not satisfy the condition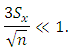 If we use the transformation
If we use the transformation 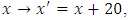 then the new auxiliary variable
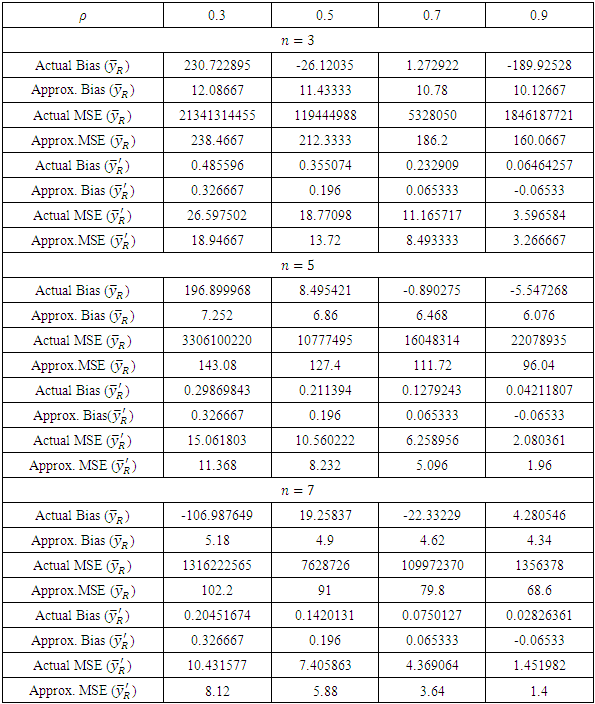
then the new auxiliary variable 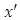 satisfies the above condition. Actual and approximate values for the biases and MSEs of the usual ratio estimator
satisfies the above condition. Actual and approximate values for the biases and MSEs of the usual ratio estimator 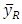 and the modified ratio estimator
and the modified ratio estimator 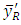 after using transformation
after using transformation 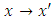 are given in Table-1.
are given in Table-1.
|
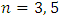
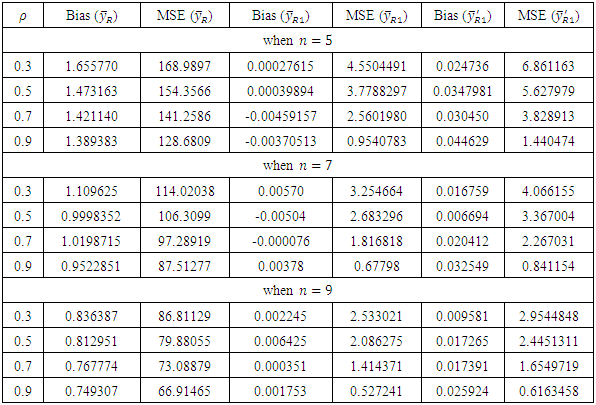
 have been drawn from each of normal population
have been drawn from each of normal population 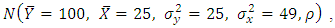 where
where 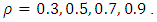 The values of biases and MSEs of
The values of biases and MSEs of 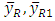 and
and 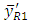 have been presented in Table-2.
have been presented in Table-2.
|
7. Conclusions
- A number of modified ratio estimators have been proposed by different researchers using the additional known information of auxiliary variable. Basically, they have applied a transformation on auxiliary variable by adding some unit-less quantity or a quantity with different units in auxiliary variable. Such type of transformations are mathematically not correct. But from these modified ratio estimators, one can form an idea that the change of origin of auxiliary variable affect the efficiency of the ratio estimator. In the present paper, it has been shown that the efficiency of ratio estimator also depends upon the origin of the auxiliary and study variables. Also, the efficiencies of the modified estimators have improved due to the change of origin and not due to additional known information of auxiliary variable. Further, the conditions for validity of the approximate results for ratio estimators have been developed in (2) and (3), which can easily be checked in practical situations before using the ratio estimators.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML