Applied Mathematics

p-ISSN: 2163-1409    e-ISSN: 2163-1425

2016;  6(2): 21-24

doi:10.5923/j.am.20160602.01

 

The Wiener Index and Hosoya Polynomial of the Subdivision Graph of the Wheel S(Wn) and the Line Graph Subdivision Graph of the Wheel L(S(Wn))

Mohammad Reza Farahani 1, Muhammad Kamran Jamil 2, M. R. Rajesh Kanna 3, Sunilkumar M. Hosamani 4

1Department of Applied Mathematics of Iran University of Science and Technology (IUST), Tehran, Iran

2Department of Mathematics, Riphah Institute of Computing and Applied Sciences (RICAS), Riphah International University, Lahore, Pakistan

3Department of Mathematics, Maharani's Science College for Women, Mysore, India

4Department of Mathematics, Rani Channamma University, Belgavi, India

Correspondence to: Mohammad Reza Farahani , Department of Applied Mathematics of Iran University of Science and Technology (IUST), Tehran, Iran.

Email:

Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.

This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract

Let G be a connected graph. The Wiener index of a graph is defined as the sum of all distances between different vertices, and the Hosoya polynomial of a graph G is defined as 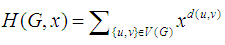. In this paper, we find the Wiener index and Hosoya polynomial of the line graphs of the wheel graphs using the concept of subdivision.

Keywords: Subdivision Graphs, Line Graphs, Wheel Wn, Wiener Index, Hosoya polynomial

Cite this paper: Mohammad Reza Farahani , Muhammad Kamran Jamil , M. R. Rajesh Kanna , Sunilkumar M. Hosamani , The Wiener Index and Hosoya Polynomial of the Subdivision Graph of the Wheel S(Wn) and the Line Graph Subdivision Graph of the Wheel L(S(Wn)), Applied Mathematics, Vol. 6 No. 2, 2016, pp. 21-24. doi: 10.5923/j.am.20160602.01.

Article Outline

1. Introduction
2. Main Results
3. Conclusions

1. Introduction

Let G=(V(G),E(G)) be a simple connected and finite graph, where V(G) and E(G) are the sets of vertices and edges, respectively. Number of elements in V(G), |V(G)|, is called the order of the graph G and the number of elements in E(G), |E(G)|, is called the size of the graph G. We will denote the order and the size by n and m, respectively. For vertices 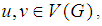the distance between u and v is the length of shortest u-v path and denoted as 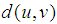. The diameter, d(G), is the largest distance between any two vertices of a graph G. For a vertex 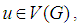degree of u is the number of first neighbours of u in G.
The subdivision graph, S(G), is the graph obtained by inserting an additional vertex into each edge of G, in other words by replacing each of its edge by a path of length 2. The line graph, L(G), of a graph G is the graph whose vertices are the edges of G, two vertices e and f are incident if and only if they have a common end vertex in G. A wheel graph with n vertices, Wn, is a graph formed by connecting a single vertex to all vertices of a cycle. A wheel graph with n vertices has 2(n-1) edges. For further details and results see [1-7].
A topological index is a function 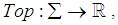where 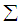is the set of finite simple graphs with the property that 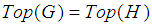if G and H are isomorphic. There is a lot of research has been done on topological indices of different graph families so far, and is of much importance due to their chemical significance.
One of the oldest topological index which is the Wiener index was introduced by chemist Harold Wiener in 1947 [8, 9]. He introduced this index for comparing and describing the relation between Physical-Chemical properties. The definition of this index is as follows:
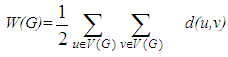The Wiener index of many molecular graphs has been computed, for details see [10-14]. The Hosoya polynomial was first introduced by H. Hosoya [15] and defines as follow:
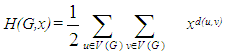A lot of research on the Hosoya polynomial of many molecular graphs has been done. For more details and chemical applications and mathematical properties of these topological indices see paper series [16-28].
Let d(G,k) be the number of vertex pairs of G, the distance of which is equal to k. Then we can rewrite the Hosoya polynomial and the Wiener index as
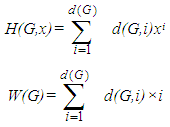where d(G) be the diameter of G and is the longest topological distance in G.

2. Main Results

Theorem 1: Let S(Wn) be the subdivision graph of a wheel graph with order n. Then the Hosoya polynomial and the Wiener index of S(Wn) are equals to:
H(S(Wn),x)=4n x+½n(n+9)x2+n(n+2)x3 +½n(3n-5)x4+ n(n-4) x5+ ½n(n-5)x6.
and
W(S(Wn))=18n2-33n.
Proof of Theorem 1: Consider the subdivision graph of a wheel graph with order n, we denotes this graph by S(Wn) for all positive integer number n≥3. By the definition of the subdivision graph of graph and from Figure 1, we can see that the size of vertex set V(S(Wn)) is equal to |V(Wn )|+ |E(Wn )|=n+1+2n=3n+1, where 2n vertices of the subdivision graph of the wheel graph Wn have degree two, similar to the wheel graph Wn, and only one center vertex c of the wheel graph Wn and the subdivision graph of the wheel graph S(Wn) has degree n. Then all remained vertices have degree two, the vertices added to the wheel graph Wn. In other words, we can divide the vertex set V(S(Wn)) into several partitions V2, V3 and Vm, on based the degree of its members as follow:
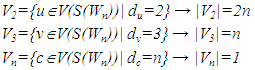So these imply that the size of edge set E(S(Wn)) is equal to
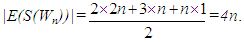Form the definitions of the Wiener index and Hosoya polynomial of a graph G, one can see that it is enough to compute all terms d(S(Wn),k) of the subdivision graph of the wheel graph S(Wn), where d(S(Wn),k) denote the number of unordered pairs of vertices x and y of S(Wn) such that distance d(x,y)=k (1≤k≤d(S(Wn))). Also, by according to Figure 1, we can see that d(S(Wn))=6, obviously.
Thus we have two re-formulas of the Wiener index and Hosoya polynomial of S(Wn) as follow:
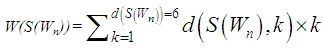and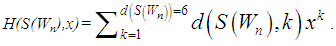
By the definitions of the Wiener index and Hosoya polynomial of G, we see that the first term of H(S(Wn),x) is equal to the number of edges of S(Wn)¸ thus d(S(Wn),1) = |E(S(Wn))| = 4n.
By Figure 1 and the definition of the subdivision graph of G, we see that there are n 2-edges paths between the Centre vertex c and the members of V3 and n 2-edges paths between all members of V3. Also, for vertices from V2 we see that there are ½[2n+n(n-1)+4n]= ½(n2+5n) 2-edges paths between them. Thus, the second term d(S(Wn),2) is equal to ½(n2+9n).
Now, for the third terms of the Wiener index and Hosoya polynomial of S(Wn), we start from the Centre vertex c, we have n 3-edges paths until the members of V2. Also there are n(n-1)+2n=n(n+1) 3-edges paths start from a vertex v of V3 and end to a vertex u of V2 and there is not any 3-edges path between all pairs of vertices (V2, V2), (V2, Vn) and (V3, V3). These imply that d(S(Wn),3) is equal to n2+2n.
From Figure 1, we see that there is not any 4-edges path with the Centre vertex c and between all members of V2 and V3. But there are n(n-2)+n= n2-n 4-edges paths between all vertices from member of V2, and there are ½n(n-3) 4-edges paths between all vertices from V3. Thus, the number of the 4-edges paths of the subdivision graph of the wheel graph S (Wn), is n2-n+½n (n-3) and d(S(Wn),4) is equal to ½n(3n-5).
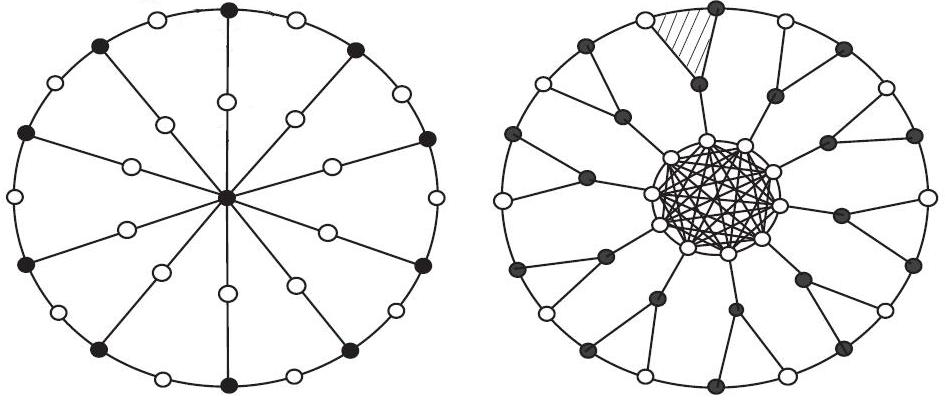Figure 1. [1, 2] The subdivision graph of the wheel Wn and the line graph subdivision graph of the wheel L(S(Wn)) for all positive integer number n≥3
For d(S(Wn),5), from Figure 1, one can see that there is not any 5-edges path between all pairs of vertices (V2, V2), (V2, Vn), (V3, V3), and (V3, Vn) obviously. And we have only n(n-4) 5-edges paths by start from a vertex v of V3 and end to a vertex u of V2 and the last term of the Wiener index and Hosoya polynomial of S(Wn) is d(S(Wn),5)=n(n-4).
Finally, from the structure of the subdivision graph of the wheel graph S(Wn), we see that there are only ½n(n-5) 6-edges paths between all pairs of vertices from the vertex partition V2, thus d(S(Wn),6)= ½n(n-5).
Here, by these above mentions results, we have the clearly formulas for the Wiener index and the Hosoya polynomial of the subdivision graph of the wheel graph S(Wn) as:
H(S(Wn),x)=Σd=1 6 d(S(Wn),d)xd
=4n x+½n(n+9)x2+n(n+2)x3+½n(3n-5)x4 + n(n-4) x5+ ½n(n-5)x6.
And also,
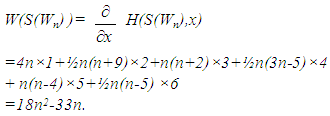Also, by definition of the Hosoya polynomial of an arbitrary graph G as order n (|V(G)|=n), it is obvious that
And, we can check
And this complete the proof of theorem 1.
Theorem 2. Consider the line graph of the subdivision graph of the wheel graph L(S(Wn)) for all positive integer number n≥3. Then,
● The Hosoya polynomial of L(S(Wn)) is equal to
H(L(S(Wn)),x)=½n(n+9)x+n(n+5)x2 +½n(5n+3)x3+2n(n-2)x4+ n(n-9)x5.
● The Wiener polynomial of L(S(Wn)) is equal to
W(L(S(Wn)) )=17n2-34n.
Proof of Theorem 2: Let L(S(Wn)) be the line graph of the subdivision graph of the wheel graph (Figure 1). The number of vertices in this graph is equal to the number of edge of the subdivision graph of the wheel graph S(Wn) and |V(L(S(Wn)) )|=4n, where n vertices of the line graph of the subdivision graph of the wheel graph L(S(Wn)) have degree n=|V(Kn-1)|+1 and all other vertices have degree three. So, we divide the vertex set of L(S(Wn)) into two partitions V3 and Vm and obviously
Here, we named all members of the vertex partition Vn as the Centre vertices.
Thus, the size of edge set E(L(S(Wn)) ) is equal to
|E(L(S(Wn)) )|=½[n×n+3×3n] =½n(n+9).
Or
|E(L(S(Wn)) )|=5n+|E(Kn)|=5n+½n(n-1) =½n(n+9).
Of course by definition of the line graph of an arbitrary graph G, it is obvious
|E(L(G))| = d(G,2),
|E(L(G))| = d(L(G),1).
New, similar to above proof of Theorem 1, to achieve our aims it is enough, we compute all terms d(L(S(Wn)),i) for all i=1,..., d(L(S(Wn)) ) (which from Figure 1, one can see that the diameter of the line graph of the subdivision graph of the wheel graph L(S(Wn)) d(L(S(Wn))) is equal to 5).
Obviously, by above equations, we know that
d(L(S(Wn)),1) =|E(L(S(Wn)) )|= d(S(Wn)),2) =½n(n+9).
On the other hand from the structure of L(S(Wn)) (Figure 1), d(L(S(Wn)),2) =n2+5n. Since, there are ½[2n+2n]+2n 2-edges paths between all vertices of the vertex partition V3. There are n+n+n(n-1) Centre vertices c∈Vn⊂V(L(S(Wn)) ) and vertices from V3.
From Figure 1, one can see that d(L(S(Wn)),3) =½n(5n+3), because 2n(n-1) 3-edges paths start from the Centre vertices of Vn and end to the vertices of the vertex partition V3. Also, there are 2n+½n(n-1)+2n=½n(n+7) 3-edges paths between all members of V3.
For d(L(S(Wn)),4), we see that there is not any 4-edges path started from the Centre vertices c and between all members of Vn and V3. And only there are 2n+2n(n-3)= 2n2-4n 4-edges paths between all member of V3. Thus, the number of the 4-edges paths of the line graph of the subdivision graph of the wheel graph L(S(Wn)) is equal to 2n(n-2).
Finally, from the structure of L(S(Wn)) (Figure 1), we see that there are ½(2n)(n-9) 5-edges paths between all vertices from V3. Therefor the last terms of the Hosoya polynomial of L(S(Wn)) is equal to d(L(S(Wn)),5) =n(n-9).
Now, these above computations imply that the Hosoya polynomial of the line graph of the subdivision graph of the wheel graph L(S(Wn)) will be
H(L(S(Wn)),x)=Σd=1 5 d(L(S(Wn)), d)xd
=½n(n+9)x+n(n+5)x2+½n(5n+3)x3+2n(n-2)x4+n(n-9)x5.
And obviously
Here the proof of theorem is completed.

3. Conclusions

In this paper, we discuss one of the oldest and thoroughly studied distance based topological index, the Wiener index, and the Hosoya polynomial. We found the Wiener index and Hosoya polynomial of the subdivision graph of the wheel Wn and the line graph subdivision graph of the wheel L(S(Wn)) for all positive integer number n≥3.

References

[1]  G. Su, L. Xu, Topological indices of the line graph of subdivision graphs and their Schur-bounds, Applied Mathematics and Computation 253 (2015) 395-401. http://dx.doi.org/10.1016/j.amc.2014.10.053.
[2]  M. F. Nadeem, S. Zafar, Z. Zahid, On certain topological indices of the line graph of subdivision graphs, Applied Mathematics and Computation 271 (2015) 790-794. http://dx.doi.org/10.1016/j.amc.2015.09.061.
[3]  M. F. Nadeem, S. Zafar, Z. Zahid. On topological properties of the line graphs of subdivision graphs of certain nanostructures, Applied Mathematics and Computation 273 (2016) 125-130.
[4]  R. Marinescu-Ghemeci, G. Mihai, I. Tomescu. Radio number of uniform subdivisions of the wheel. Utilitas Mathematica · March 2015.https://www.researchgate.net/publication/295591125.
[5]  S.M. Hosamani and S. Zafar. On topological properties of the line graphs of subdivision graphs of certain nanostructures – II. Researchgate. December 2015.https://www.researchgate.net/publication/287642588.
[6]  M. Azari, A. Iranmanesh, and T. Doslic. Vertex-weighted Wiener polynomials of subdivision-related graphs. Opuscula Math. 36(1), (2016), 5–23.http://dx.doi.org/10.7494/OpMath.2016.36.1.5.
[7]  M.R. Farahani, M.K. Jamil, Schultz Polynomial of Subdivision Graphs and Line Graphs of Wn. Journal of Chemical and Pharmaceutical Research. 8(3), 2016, 51-57. http://jocpr.com/vol8-iss3.html.
[8]  H. Wiener, Structural determination of paraffin boiling points, J. Amer. Chem. Soc. 69 (1947) 17-20.
[9]  H. Wiener, Relations of the physical properties of the isomeric alkanes to molecular structure: surface tension, specific dispersion, and critical solution temperature in aniline, J. Phys. Chem. 52 (1948) 1082-1089.
[10]  I. Gutman, S. Klavžar, A method for calculating Wiener numbers of Benzenoid hydrocarbons and phenylens, ACH Models Chem. 133 (1996) 389-399.
[11]  B. Zhou, I. Gutman, Relations between Wiener, hyper-Wiener and Zagreb indices, Chem. Phys. Letters, 394 (2004) 93-95.
[12]  B. Y. Yang, Y. N. Yeh, A crowning moment for Wiener indices, Stud. Appl. Math. 112 (2004) 333-340.
[13]  W. Yan, B. Y. Yang and Y. N. Yeh, The behaviour of Wiener indices and polynomials of graph under five graph decorations, Appl. Math. Lett. 20 (2007) 290-295.
[14]  S. Nikolić, N. Trinajstić, Z. Mihalić, The Wiener index: Development and applications, Croat. Chem. Acta. 68 (1995) 105-129.
[15]  H. Hosoya, On some counting polynomials in chemistry, Disc. Appl. Math. 19 (1989) 239-257.
[16]  I. Gutman, Hosoya polynomial and the distance of the total graph of a tree. Publikacije Elektrotechnikog Fakulteta, Univerzitetu Beogradu, 10 (1999) 53.
[17]  M. R. Farahani, Hosoya polynomial, Wiener and hyper-Wiener indices of some regular graphs. Informatics Engineering, an International Journal 1(1) Dec (2013) 9-13.
[18]  S. Xu, H. Zhang, Generalized Hosoya polynomials of hexagonal chains, J. Math. Chem. 43 (2008).
[19]  A.R. Ashrafi, H. Shabani, The Hosoya polynomial of TUC4C8 Nanotubes, Digest. J. Nanomater. Bios. 4(3) (2009) 453-457.
[20]  M. R. Farahani, Hosoya polynomial and Wiener index of Jahangir graphs J2,,M, Pacific Journal of Applied Mathematics, 7 (3). In press.
[21]  M.R. Farahani, M.P. Vlad. On the Schultz, Modified Schultz and Hosoya polynomials and Derived Indices of Capra-designed planar Benzenoid. Studia UBB Chemia. 57(4), (2012), 55-63.
[22]  M.R. Farahani, On the Schultz polynomial, Modified Schultz polynomial, Hosoya polynomial and Wiener index of Circumcoronene series of Benzenoid. Journal of Applied Mathematics & Informatics. 31(5-6), (2013). 595-608. http://dx.doi.org/10.14317/jami.2013.595.
[23]  M.R. Farahani, Hosoya, Schultz, Modified Schultz Polynomials and Their Topological Indices of Benzene Molecules: First Members of Polycyclic Aromatic Hydrocarbons (PAHs). International Journal of Theoretical Chemistry. 1(2), October (2013), 09-16.http://acascipub.com/Journals.php.
[24]  M.R. Farahani, Hosoya polynomial, Wiener and Hyper-Wiener indices of some regular graphs. Informatics Engineering, an International Journal. 1(1), (2013), 9-13. http://airccse.org/journal/ieij/current.html.
[25]  M.R. Farahani, The Wiener Index and Hosoya polynomial of a class of Jahangir graphs J3,m. Fundamental Journal of Mathematics and Mathematical Science. 3(1), 2015, 91-96. http://frdint.com/math_and_mathe_sciences_volume_three_%20issue_one_two_zero_fifteen.html.
[26]  M.R. Farahani, Hosoya Polynomial of Jahangir graphs J4,m. Global Journal of Mathematics, 3(1), 2015, 232-236.
[27]  M.R. Farahani, Wei Gao and M.R. Rajesh Kanna. The Schultz, Modified Schultz indices and their polynomials of the Jahangir graphs Jn,m for integer numbers n=3, m>1. Asian Journal of Applied Sciences. 2015, 3(6), 823-827. http://www.ajouronline.com.
[28]  M.R. Farahani and M.R. Rajesh Kanna. Computing Hosoya Polynomial, Wiener Index and Hyper-Wiener Index of Harary graph. Applied Mathematics, 5(5), 2015, 93-96. DOI: 10.5923/j.am.20150505.01.