1. Introduction

Life in the today modern and complicated world requires creative thoughts and dynamic ideas. Learning math effectively, can help it to form and grow well. Studying the effective parameters in learning math has been attractive to many scientists in the field of education during recent decades. Many researches have been performed and the results show that, understanding mathematics not only depends on cognitive structures, but also on motivational and emotional factors such as belief, attitudes, and anxiety. McLeod (1992) in the field of math education believes that efforts for revising math education program must discriminate for the role of interest. If the research for instruction and learning is to maximize its impact on the students and teachers, then in the researchers’ minds, emotional factors must have central role.

There is an interaction between learning and attitudes. The individuals’ learning can affect attitudes and conversely, the attitudes can affect their learning. Therefore, sometimes the differences in the learned behavior are because of the people’s belief and perceptions (Dweck, and Leggett, 1988). Study in the field of attitude towards mathematics and its role in educational achievement have been started with Iken and Dragger (1961) and Iken (1979). The findings of Iken and Dragger showed that attitude towards mathematics are based on a few scopes such as enjoying math homework and the fear of facing situation in which mathematics is used. In most studies, attitude towards math has been reported as an important factor in educational achievement (e.g. Ma, 1997; Ma and Xu, 2004).

Hackett and Betz (1989) have defined math self-efficacy as an assessment of people’s self-confidence in their ability for successful task performing or math specific problem. This factor can also effect on educational achievement in math, positively (Liu and Koirala, 2009; Nicolaidou and Philippou, 2003). It has been shown in some studies that both factors, attitude towards math and self-efficacy in math have positive relationship. They have also positive significant effect on educational achievement in mathematics (Nicolaidou and Philippou, 2003).

Figure 1. Primary path plot

There are very little research on studying the relationship between math performance and self-efficacy variables with attitude towards mathematics, while having variables such as gender, failing in math, and the pass mark (pre-score). Therefore, the research goal is to investigate the relationship between self-efficacy and educational achievement in math, while controlling the students’ attitude towards math using structure modeling method.

According to the proposed model, the following test must be investigated in society for being justified. Fig. 1 demonstrates causality model for math performance using research variables. In this model, gender and failing in math variables, are exogenous variables. Variables of math previous score and self-efficacy, attitude towards math and math current score, are endogenous variables in this model.

2. Method

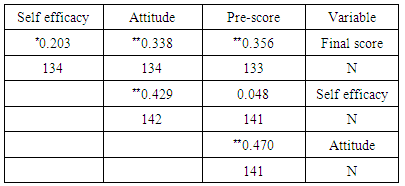
The main objective of the research is applied research and in terms of data collection it is descriptive correlational research. Statistical population of this research is the students of Islamic Azad University, Abadan branch, studying in the spring semester, 2015. The method of sampling is multi-stage cluster. Among Chemistry engineering and Electrical engineering students of four classes, in which all the students were taught from the same basic mathematics books, sampling was performed. The collected samples include 142 students (101 men and 41 women). The mean and standard deviation of the age is 24.21 and 6.906 years, respectively. The participants are from a wide age range. Also, among 142 participants in this research, one person did not mention its name. Minimum age of 18 years old and maximum of 50 years old was registered. To measure educational achievement in math, final grade has been considered. It is worth mentioning that basic mathematics final exam was held in common. Attitude towards mathematics contains 13 items which are measured by 4-point Likert (1: strongly disagree to 4: strongly agree). The sum of 13 items in this research shows the attitude towards mathematics. To measure math self-efficacy, Ferla, Valcke, and Cai (2009) questionnaire has been used. This questionnaire contains 8 items which are measured by 4-point Likert (1: very reliable to 4: very unreliable). Cronbach’s alpha value was calculated 0.885 and 0.68 for attitude towards mathematics and self-efficacy, respectively. Data analysis was performed in three states: first, distributing of the research variables has been descriptively investigated. Second, the correlation between research variables has been analyzed. Finally, by the use of this analysis, the research model path is investigated.

3. Findings

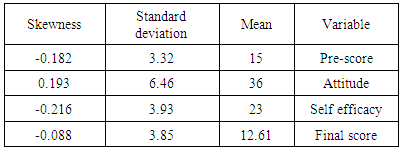
Table 1 shows descriptive statistics for subscales of available quantitative variables in reported hypothesizes. Eight people were absent in the final math exam. The mean grade of the final exam is 12.61±3.85. The previous students had a mean grade of 15±3.32. The skewness index for all variables is less than 0.22. Therefore, in terms of symmetry, variables status is normal.

Table 1. Descriptive statistics for quantitative variables of the research

In Table 2, correlation between variables of the research is observed. As it is observed from Table 2, there is a direct significant relationship between final grade of mathematics with previous grade variables (r=0.356, p<0.01) and attitude towards mathematics (r=0.338, p<0.01). Final grade of the mathematics has direct significant relationship with self-efficacy variable in 5% error level (r=0.356, p<0.01). Previous grade of the math has direct significant relationship with attitude towards mathematics in 1% error level. Previous grade of the math does not have a significant relationship with math self-efficacy in 5% error level (r=0.048, p>0.05). Self-efficacy variables have positive significant relationship with attitude towards mathematics in 1% error level.

Table 2. Correlation matrices of the research variables

Fitting indicators of the structure model for Fig. 1 is given in Table 3. Null hypothesis indicates that theoretical model is available in the population. According to the Table, chi-squared value in 5% error level is not significant; we do not refuse null hypothesis (Χ² = 8.402 and p = 0.135). In other words, the theoretical model presented by this data is acceptable in the population.

Table 3. Fitting indexes for the theoretical model of educational achievement

Fitting indicators for the new model is given in Table 3. As we can observe from the Table, the index Χ²/df is less than 2. The lower bound of the confidence interval 90% for RMSEA is less than 0.08. CFI and IFI Indexes are more than 0.9. Goodness of fit index of GFI and NFI is also more than cut-off point, 0.9. Therefore, the proposed model has a perfect fit in the statistical population. Fig. 2 indicates estimating the factors of the presented route. As it is shown in Fig. 2, the route factors of the model exogenous variables are negative attitude towards mathematics. The sign of route factors match with the theoretical factors presented in Fig. 2.

In Table 4, the significance level of each route has been reported for the total effects. The total effect of failing in math on previous grade variables, attitude towards math in 1% error level, and final grade of math in 5% error level is significant. All these effects are negative which indicates reducing math performance. The variable gender has a significant effect on self-efficacy, attitude, and final grade in 5% error level and all the effects are positive. Male students showed better performance than female in mathematics. The total effect of the previous grade on final grade is positively significant in 5% error level. This variable has positive effect on attitude towards mathematics in 1% error level. It means better previous performance makes attitude better. The effect of self-efficacy on attitude is not significant. Whereas, its effect on the final grade is positive and it is significant in 1% error level. The total effect of attitude on final grade is not significant in 5% error level.

Table 4. Level of significance for the total effects of the model

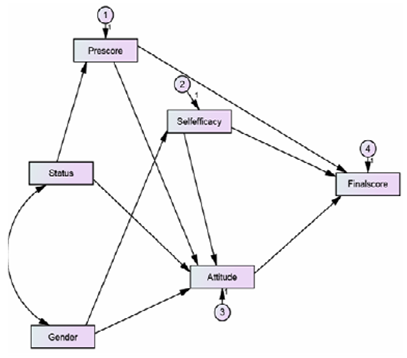
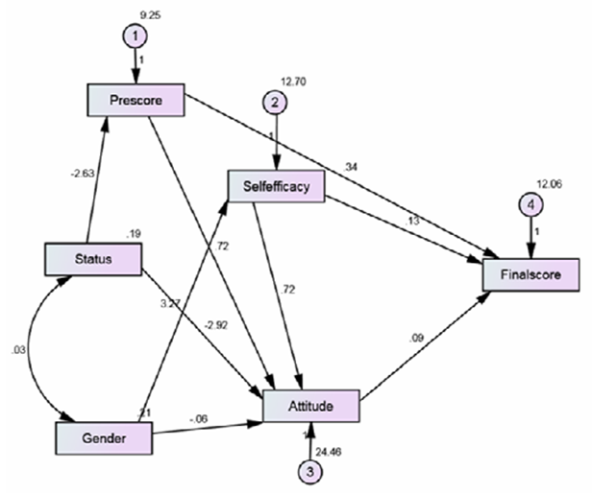Figure 2. Estimating the parameters of the theoretical model

4. Discussions

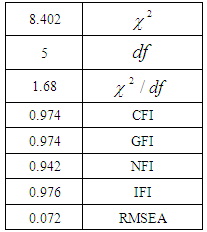
The aim of this study is to identify the students’ self-efficacy beliefs in mathematics and the use of these beliefs for predicting the progress of students’ math and the relationship between attitude and educational achievement. Each model for learning and mathematics achievement can be used by the educational consultants and teachers of mathematics. The proposed model in this study was verified and it is concluded that, even though correlation between attitude and the grade was significant, and the value was even more than the value for simple correlation between self-efficacy and final grade; in the proposed model, the total effect of attitude on math performance has not been significant. The results show that there is a positive significant relationship between self-efficacy and mathematics achievement. Therefore, we can claim that high positive self-efficacy has positive impact on mathematics achievement. In contrast, low self-efficacy may have negative impact on students’ mathematics achievement. Therefore, teachers can predict educational status of the students, or to help scholars in order to increase their self-efficacy.

ACKNOWLEDGEMENTS

This article is resulted from a research project which financed by Islamic Azad University Abadan branch.