Hassan Ibrahim 1, Francis Attah 1, Gabriel T. Gyegwe 2
1Department of Mathematics, Federal University Lafia, Lafia, Nigeria
2Department of Math/Stat./Comp. Sci., University of Agriculture Makurdi, Makurdi, Nigeria
Correspondence to: Hassan Ibrahim , Department of Mathematics, Federal University Lafia, Lafia, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, new iterative method proposed by Daftadar-Gejji and Jafari (2006) was used in solving both linear and nonlinear Volterra-Fredholm and Mixed Volterra-Fredholm integral equations. The method yields a series with faster convergence. Finally, some concrete examples are given to illustrate the validity of the method.
Keywords:
Volterra-Fredholm Integral equation, New iterative method, Mixed Volterra-Fredholm integral equation, Convergence Analysis
Cite this paper: Hassan Ibrahim , Francis Attah , Gabriel T. Gyegwe , On the Solution of Volterra-Fredholm and Mixed Volterra-Fredholm Integral Equations Using the New Iterative Method, Applied Mathematics, Vol. 6 No. 1, 2016, pp. 1-5. doi: 10.5923/j.am.20160601.01.
1. Introduction
Volterra-Fredholm Integral equations have received considerable interest in the Mathematical Physics, engineering, biology and contact problems in the theory of elasticity (see [1-5]). The solution of these integral equations can be obtained both analytically and numerically using one of the following method: Homotopy perturbation method [6], Rationalized Haar functions [7], Taylor polynomial method [8], Adomian decomposition method [9] and Minggen et al [10], used the representation of the exact solution for the nonlinear Volterra-Fredholm integral equations in the reproducing kernel space. The exact solution is given by the series form. In [1], Abdou used orthogonal polynomial to solve Fredholm-Volterra integral equations. Also, Yusufoglu and Erbas presented the method based on interpolation in solving linear Volterra-Fredholm integral equations [12]. Maleknejad and Sohrabi [13] solved nonlinear Volterra-Fredholm Hammerestein integral equations in terms of Legendre polynomials. Yousefi and Razzaghi in [14] applied legendre wavelets to special type of nonlinear Volterra-Fredholm integral equations of the form 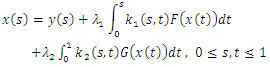 | (1) |
where 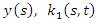 and
and 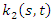 are assumed to be in
are assumed to be in 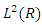 on the interval
on the interval 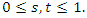
2. Review on New Iterative Method
Recently, Daftardar-Gejji and Jafari [15] proposed a new technique for solving linear and nonlinear functional equations known as the New Iterative Method. This method has proven useful for solving a variety of nonlinear equations such as algebraic equations, integral equations, ordinary and partial differential equations of integer and fractional order and systems of equations as well. Bhalekar and Daftardar-Gejji [16] applied the new iterative method to Fractional-order logistic equation. The obtained results were compared with the Adomian decomposition and Homotopy perturbation method. They concluded that the new iterative method converges faster to the approximate solutions. Ambreen et al. [17] solved time-fractional Schrödinger equations using the New Iterative Method (NIM). The technique is fully compatible with the complexity of these problems and obtained results are highly encouraging. Numerical results coupled with graphical representations explicitly reveal the complete reliability of the suggested algorithm. Daftardar-Gejji and Bhalekar [19] employed the New Iterative Method to find solutions of linear and nonlinear fractional diffusion-wave equations. The results obtained were free from rounding off errors since it does not involve discretization.Ramadan and Al-luhaibi [20] applied the new iterative method (NIM) to find approximate analytical solution of the Fornberg-Whitham equation. A comparison is made between the NIM results, homotopy perturbation transform method (HPTM) and Adomian decomposition method (ADM). It was discovered that the new iterative method solved nonlinear problems without using Adomian’s polynomials and He’s polynomials. Ibrahim and Ayoo [21] Srivastava and Rai [22]) proposed a new mathematical model, namely a multi-term fractional diffusion equation, for oxygen delivery through a capillary of tissues. They used the new iterative method (NIM) and modified Adomian decomposition method (MADM) to solve the multi-term fractional diffusion equation for different conditions. The results thus obtained are compared and presented graphically. It was observed that the order of the diffusion equation affects the delivery of oxygen significantly. The basic difference between the methods is that, the New Iterative Method (NIM) is direct and straightforward and it avoids the volume of calculations resulting from computing the Adomain polynomials.Hemeda [23] obtained the solution of fractional difference equations using the new iterative method (NIM). The obtained results confirmed the power of the method in reducing the size of calculations compared with other traditional methods. Kocak and Yildrim [24] applied new iterative method in finding the exact solutions of nonlinear time-fractional partial differential equations. The fractional derivatives are described in the Caputo sense. Yaseen et al. [25] used the iterative method to find an analytic treatment for Laplace equation with Dirichlet and Neumann boundary conditions. The obtained results show that the present approach is highly accurate and requires reduced amount of calculations compared with the existing iterative methods.It can be concluded that the New Iterative method (NIM) is a useful technique for solving both linear and nonlinear problems, most especially, in sciences and engineering.In this paper, we consider the linear Volterra-Fredholm and mixed Volterra-Fredholm integral equation of the form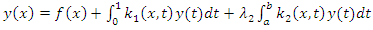 | (2) |
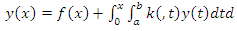 | (3) |
respectively, where 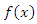 and
and 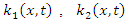 and
and 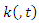 are analytic functions.
are analytic functions. 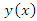 is the unknown function. We also consider nonlinear Fredholm-Volterra integral equation is the type
is the unknown function. We also consider nonlinear Fredholm-Volterra integral equation is the type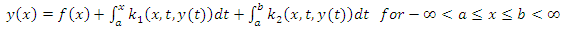 | (4) |
Where 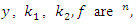 the n-dimensional Euclidean space with appropriate norm denoted by
the n-dimensional Euclidean space with appropriate norm denoted by 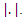
3. Basic Idea of NIM
Consider the Nonlinear function equation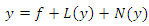 | (5) |
where 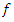 is a given function,
is a given function, 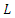 and
and 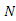 are linear and nonlinear operators respectively. It is assumed that the NIM solution for eqn (5) has the form
are linear and nonlinear operators respectively. It is assumed that the NIM solution for eqn (5) has the form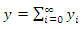 | (6) |
The convergence of series (6) is proved in [26] and described in section 3.Since L is linear,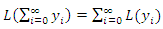 | (7) |
The nonlinear operator N in eqn (5) is decomposed by Dafterder-Gejj and Jafari [15] as below: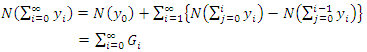 | (8) |
where 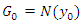 and
and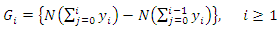 Using eqns (6), (7), (8) in eqn (5), we get
Using eqns (6), (7), (8) in eqn (5), we get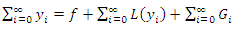 | (9) |
If N is a contraction, i.e.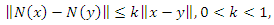 then
then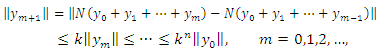 and the series
and the series 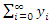 and
and 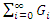 are absolutely and uniformly converges to solution of Eq. (5) [29]. Which is unique, in view of Banach fixed point theorem [30]. The k-term approximate solution of Eq. (2-4) is given by
are absolutely and uniformly converges to solution of Eq. (5) [29]. Which is unique, in view of Banach fixed point theorem [30]. The k-term approximate solution of Eq. (2-4) is given by 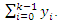
4. Condition of NIM
The following convergence result for NIM is described by Daftardar-Gejji and Bhalekar.Theorem 1. [26] if N is 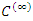 in a neighborhood of
in a neighborhood of 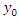 and
and 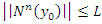 for any n and for some real
for any n and for some real 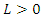 and
and 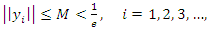 then the series
then the series 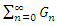 is absolutely convergent to N and moreover
is absolutely convergent to N and moreover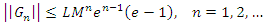 Theorem 2. [26] if N is
Theorem 2. [26] if N is 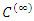 and
and 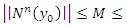
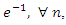 then the series
then the series 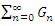 is absolutely convergent to N.
is absolutely convergent to N.
5. Numerical Examples
In this section, we present the numerical result of some problems solved by the proposed method of this article.Example 1: Consider the linear Volterra-Fredholm integral equation [27]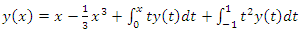 | (10) |
Using NIM, we get an iterative scheme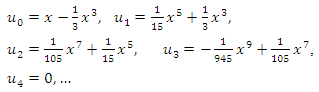 Thus, the solution (10) is
Thus, the solution (10) is 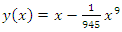
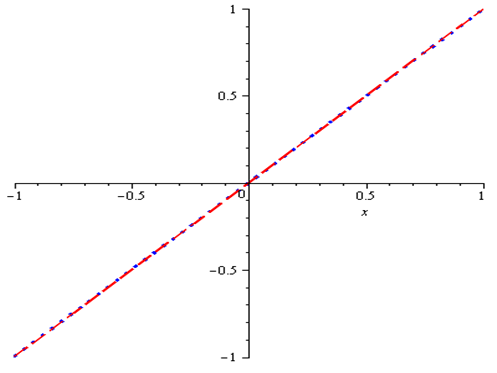 | Figure 1. Exact and Approximate Solution of Example 1, where dash and dotted lines represents the approximate and exact solution respectively |
Example 2: Consider the linear mixed Volterra-Fredholm integral equations,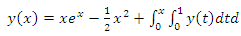 | (11) |
This NIM leads to 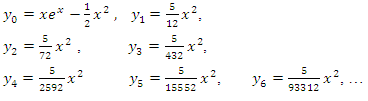 Thus the solution of (11) is
Thus the solution of (11) is 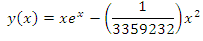
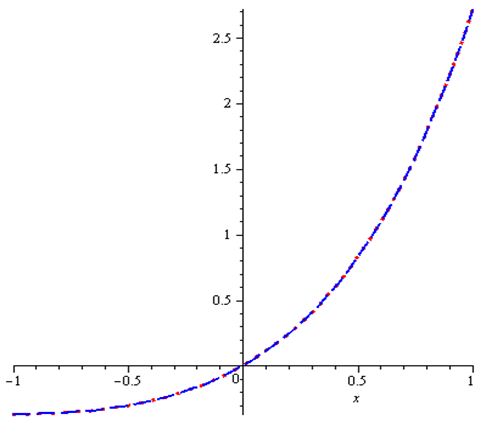 | Figure 2. Exact and Approximate Solution of Example 2, where dash and dotted lines represents the approximate and exact solution respectively |
Example 3: Consider the nonlinear Volterra-Fredholm integral equation [28]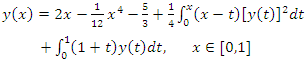 | (12) |
with exact solution 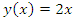 Applying NIM to (12), we get
Applying NIM to (12), we get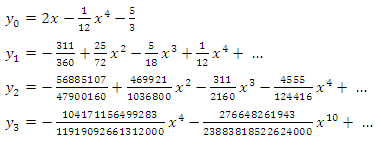 Thus the solution of (12) is
Thus the solution of (12) is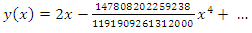
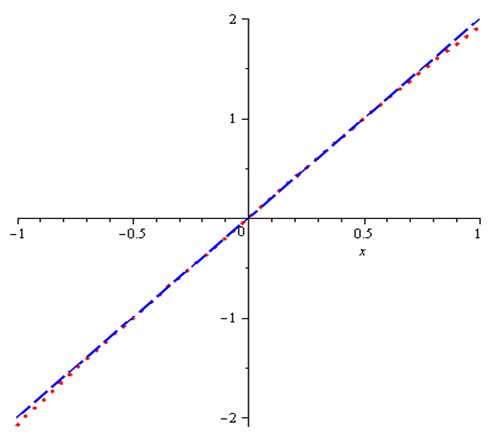 | Figure 3. Exact and Approximate Solution of Example 3, where dash and dotted lines represents the approximate and exact solution respectively |
Table 1. Results for Example 1
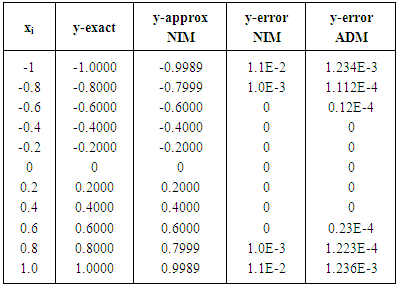 |
| |
|
Table 1 shows the computed error of the proposed method and compares the results with the Adomian decomposition method. Table 1 shows that our results are considerable accurate as the error of the NIM is lesser than that of ADM.Table 2. Results for Example 2
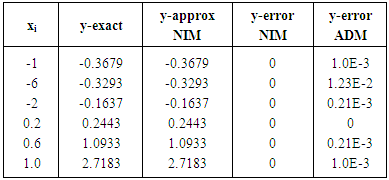 |
| |
|
In Table 2, computed error shows that the value of the exact and approximated solutions of the proposed method are the same, comparing this error with that of ADM, we see that, the proposed method converge accurately to the exact solution of Example 2.Table 3. Results for Example 3
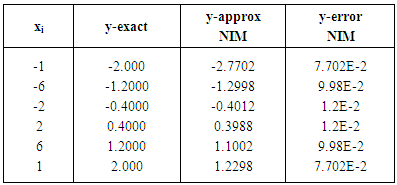 |
| |
|
6. Conclusions
We have successfully utilized new iterative method (NIM) to obtain semi-analytical solutions of both Volterra-Fredholm and mixed Volterra-Fredholm integral equations. The solution obtained and exact solutions are plotted using Maple 13 software. It is observed that the present method reduces the computational difficulties of other traditional methods and all the calculation can be made in simple manipulations. The accuracy of the obtained solutions can be improved by taking more iteration in the solutions. In many cases, the series solution obtained with NIM can be written in exact closed form. The solutions obtained are highly in agreement with the exact solutions.
ACKNOWLEDGEMENTS
H. Ibrahim acknowledges Dr. Terhemen Aboiyar of the University of Agriculture Makurdi, Nigeria for his support towards the success of this article.
References
| [1] | C. Consterda, Integral equation of the first kind in plane elasticity. J. Quort. Appl. Math. L(1) (4) (1995), 783-791. |
| [2] | M. A. Abdou, On asymptotic methods for fredholm-volterra integral equation of the second kind in contact problems. J. Comp. Appl. Math. 154 (2003), 431-446. |
| [3] | M. A. Abdou, F. A. Salama, Volterra-fredholm integral equation of the first kind and spectral relationships, Appl. Math. Comput. 153 (2004), 141-153. |
| [4] | M. I. Muskhelishvili, Some Basic problems of Mathematical theory of Elasticity, Noordhoff, Holland, 1953. |
| [5] | V. M. Aleksandrov, E. V. Kovalenko and S. M. Makhitarien; On a method of obtaining spectral relationships for integral operators of mixed problems of mechanics of continuous media, Appl. Math. Mech. 46 (6) (1983), 825-832. |
| [6] | M. Ghasani, M. Tavassoli Kajani and E. Babolian; Numerical solution of the nonlinear volterra-fredholm integral equations by using homotopy perturbation method. Appl. Matt. Comput., 188 (2007), 446-449. |
| [7] | Y. Ordokhani,; Solution of nonlinear volterra-fredholm-Hammerstein integral equations via rationalized Haar functions, Appl. Matt.Comput. 180 (2006) 436-443. |
| [8] | S. Yalcinbas; Taylor polynomial solutions of nonlinear volterra-fredholm integral equations, Appl. Matt. Comput. 127 (2002) 195-206. |
| [9] | K. Maleknejad, M. Hadizadeh; A new computational method for volterra- fredholm integral equations, Computer and Mathematics with Applications. 37 (9): 1-8 (1999). |
| [10] | C. Minggen and D. Hong, Representation of exact solution for the nonlinear volterra-fredholm integral equations, Appl. Math. Comput, 182 (2006), 1795-1802. |
| [11] | M.A. Abdou, Fredholm-volterra integral equation of the first kind and contact problem. Appl. Math. Comput. 125 (2002), 79-91. |
| [12] | E. Yusufoglu and E. Erbas; Numerical expansion methods for solving Volterra-Fredholm type linear integral equations by interpolation and quadrature rules. Kybernetes 37 (6), (2008) 768-785. |
| [13] | K. Maleknejad and S. Sohrabi; Legendre polynomial solution of nonlinear volterra-fredholm integral equations. Iust International Journal of Engineering Science. Vol. 19, No. 1-5, (2008) 49-52. |
| [14] | S. Yousefi and M. Razzaghi, Legendre wavelet method for the nonlinear Volterra-Fredholm integral equations. Appl. Math. Comput. 70 (2005), 1-8. |
| [15] | V. Dafterder-Gejji and H. Jafari, An iterative method for solving nonlinear functional equations. Journal of Mathematical Analysis and Applications. 316 (2006) 753-763. |
| [16] | S. Bhaleker and V. Dafterder-gejji. (2012) Solving fractional-order logistic equation using a new iterative method. Hindawi publishing corporation, international Journal of differential equations. 20: 12-16. |
| [17] | Ambreen B., K. Abid, U. Hayat, S. T. Mohyud-Ain (2013). New iterative method for Time-fractional Schrondinger Equation. World Journal of modeling and Simulation. 9: 89-95. |
| [18] | T. Aboiyar and H. Ibrahim (2015). Approximation of systems of Volterra integral Equations of the second kind using the New iterative method. International Journal of Applied Science and Mathematical Theory. 1 (4). |
| [19] | V. Dafterder-Gejji and S. Bhaleker (2008). Solving Fractional Diffussion – Wave equations using New Iterative Method. Fractional calculus and Applied Analysis: International Journal of Theory and Applications. 11: 11311-1454. |
| [20] | M. A. Ramaden and M. S. Al-luhaibi (2014). NIM for solving the Fomberg- Withan Equation and comparison with the homotopy perturbation transform method. British Journal of Mathematics and Computer Science. 4 (9) 1231-1227. |
| [21] | H. Ibrahim and P.V. Ayoo (2013). Approximation of systems of Volterra Integro-Differential Equations using the New Iterative Method. International Journal of Science and Research. Impact factor (2013): 4.438. ISSN (online): 2319-7064. |
| [22] | V. Srivastava and K. N. Rai (2010). A Multi-Term Fractional Diffusion Equation for oxygen delivery through a capillary to Tissues. Mathematical and Computer Modeling. 5: 616-624. |
| [23] | Hamada A. A. (2012). New Iterative Method: An Application for solving fractional physical Differential Equation. Hindawi Publishing Corporation. 13: 23-27. |
| [24] | H. Kocak and A. Yildrin (2011). An Effient NIM for finding exact solutions of nonlinear Time-Fractional partial differential equations. Nonlinear Analysis, modeling and control. 16: 403-414. |
| [25] | M. Yaseen, M. Samraig and S, Naheed (2012). The DI method for exact solutions of Laplace equation. International Journal of Mathematical Physics. 12: 1208-3350. |
| [26] | S. Bhaleker, V. Dafterder-Gejj. Concergence of the New iterative method. International Journal of Differential Equations, 2011. |
| [27] | A. M. Wawwaz; Linear and Nonlinear Integral equations. Methods and Applications. Higher education press. Springer pg 261-268. |
| [28] | M. Zerebnia (2013). A Numerical solution of nonlinear Volterra-Fredholm integral equations. Journal of Applied Analysis and Computation. Vol. 3(1), 95-104. |
| [29] | Cherruault, Y. (1988). Convergence of Adomain’s Decomposition Method. Kybernetes. 8:31-38. |
| [30] | Jerri, A. M. (1999). Introduction to Integral Equations with Applications. New York: Wiley. |


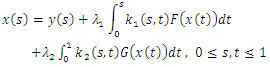
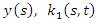 and
and 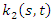 are assumed to be in
are assumed to be in 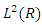 on the interval
on the interval 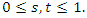
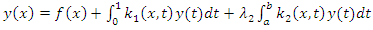
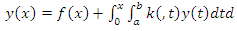
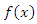 and
and 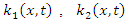 and
and 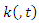 are analytic functions.
are analytic functions. 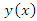 is the unknown function. We also consider nonlinear Fredholm-Volterra integral equation is the type
is the unknown function. We also consider nonlinear Fredholm-Volterra integral equation is the type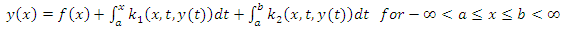
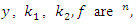 the n-dimensional Euclidean space with appropriate norm denoted by
the n-dimensional Euclidean space with appropriate norm denoted by 
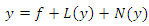
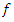 is a given function,
is a given function, 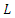 and
and 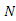 are linear and nonlinear operators respectively. It is assumed that the NIM solution for eqn (5) has the form
are linear and nonlinear operators respectively. It is assumed that the NIM solution for eqn (5) has the form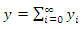
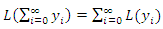
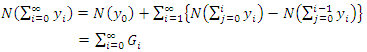
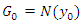 and
and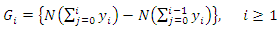 Using eqns (6), (7), (8) in eqn (5), we get
Using eqns (6), (7), (8) in eqn (5), we get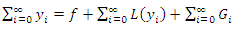
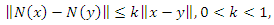 then
then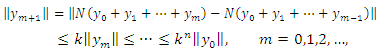 and the series
and the series 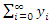 and
and 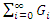 are absolutely and uniformly converges to solution of Eq. (5) [29]. Which is unique, in view of Banach fixed point theorem [30]. The k-term approximate solution of Eq. (2-4) is given by
are absolutely and uniformly converges to solution of Eq. (5) [29]. Which is unique, in view of Banach fixed point theorem [30]. The k-term approximate solution of Eq. (2-4) is given by 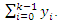
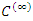 in a neighborhood of
in a neighborhood of 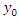 and
and 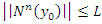 for any n and for some real
for any n and for some real 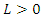 and
and 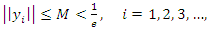 then the series
then the series 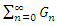 is absolutely convergent to N and moreover
is absolutely convergent to N and moreover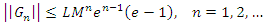 Theorem 2. [26] if N is
Theorem 2. [26] if N is 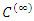 and
and 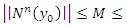
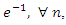 then the series
then the series 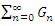 is absolutely convergent to N.
is absolutely convergent to N.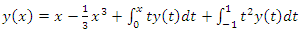
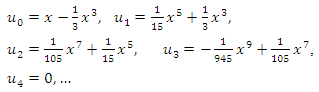 Thus, the solution (10) is
Thus, the solution (10) is 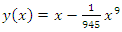

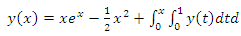
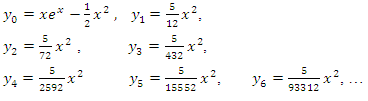 Thus the solution of (11) is
Thus the solution of (11) is 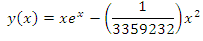

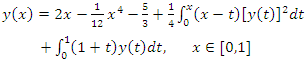
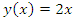 Applying NIM to (12), we get
Applying NIM to (12), we get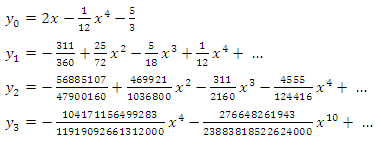 Thus the solution of (12) is
Thus the solution of (12) is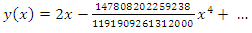

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

