-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2015; 5(6): 111-124
doi:10.5923/j.am.20150506.02

In-Plane and Out-of-Plane Dynamic Responses of Elastic Cables under External and Parametric Excitations
Usama H. Hegazy
Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine
Correspondence to: Usama H. Hegazy, Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The dynamic behavior of a three dimensional suspended elastic cable subjected to external and parametric excitations are investigated. The case of subharmonic resonance in the presence of 1:1:1 internal resonance between the modes of the cable is considered and examined. The method of multiple scales is applied to study the steady-state response and the stability of the system at resonance conditions. Numerical simulations illustrated that multiple-valued solutions, jump and saturation phenomenon, hardening and softening nonlinearities occur in the resonant frequency response curves. The effects of different parameters on system behavior have been studied applying frequency response function.
Keywords: In-Plane mode, Out-of-Plane mode, Parametric Resonance, Quadratic and cubic nonlinearities
Cite this paper: Usama H. Hegazy, In-Plane and Out-of-Plane Dynamic Responses of Elastic Cables under External and Parametric Excitations, Applied Mathematics, Vol. 5 No. 6, 2015, pp. 111-124. doi: 10.5923/j.am.20150506.02.
Article Outline
1. Introduction
- The nonlinear response of a suspended elastic cable under random excitation at 2:1 internal resonance of the first planar and non-planar modes is investigated. The Gaussian and non-Gaussian closure solutions are found to be in a good agreement with Monte-Carlo simulation. It is indicated that the mean response of the in-plane mode possesses a non-zero mean under zero mean excitation due to the non-zero sag-to-span ratio [1]. A three-mode, first in-plane mode and first two out-of-plane modes, random excitation of a suspended elastic cable with a 2:1:2 internal resonance is considered and studied. The Fokker-Planck equation and non-Gaussian closure scheme are applied to perform random analysis, which are validated using Monte Carlo simulation. The effect of some cable parameters on the autoparametric interaction is investigated [2]. The nonlinear dynamics of a two d.o.f. suspended elastic cable under small tangential oscillations of one support, which result in parametric excitation of out-of-plane motion and simultaneous parametric and external excitation of in-plane motion, are studied. A first order perturbation analysis is applied to determine the stability of the planar and non-planar periodic motions and found that suspended cables may exhibit saturation and jump phenomena. Theoretical predictions are found to be in a good agreement with experimental measurements of the cable two-to-one resonant response [3]. A second order perturbation analysis is conducted to investigate the existence and stability of periodic solutions with near commensurable natural frequencies in a two-to-one ratio. It is found that cubic nonlinearities disrupt saturation and theoretical results are confirmed by numerical integration of the equations of motion [4]. A three degree-of-freedom model of suspended elastic cable subject to planar excitation is considered and the resonant response of the system is studied when a symmetric in-plane mode interacts with two out-of-plane modes. The considered simultaneous internal resonance occurs when the natural frequency of the in-plane mode is in the neighborhood of natural frequency of the first out-of-plane mode and of twice of natural frequency of the second out-of-plane mode. The multiple scales method up to a second order is utilized to obtain periodic solutions, which are verified numerically [5]. The case of 1:1 internal resonance and primary parametric resonance of a two dimensional suspended elastic cable to parametrical excitation of out-of-plane motion and external excitations of in-plane motion is studied. The theory of normal form and method of multiple scales are used to obtain a simplified averaged equations. It is shown that the considered model may undergo Hopf bifurcation, heteroclinic bifurcations and a Silnikov type homoclinic orbit to the saddle focus. Numerical simulations are performed to illustrate the theoretical predictions [6]. A hyprid three-dimensional finite element/incremental harmonic balance method is utilized to study the nonlinear modal interaction and internal resonance of a suspended cable. It is found that response profiles of the cable at the super-harmonic resonance are very different from those at the primary and internal resonances. Moreover, strong modal interaction occurs in the transition from the primary resonance to the super-harmonic resonance, and from the superharmonic resonance to the primary resonance [7]. The nonlinear responses of immersed cable subject to constant fluid flow speed along the cable plane with two in-plane mode interaction under fluid hydrodynamic forces are investigated. It is indicated that the system exhibits a periodic attractor in the configuration plane when the velocity of the fluid is large [8]. The non-planar finite dynamics of a four d.o.f. elastic suspended cable to external excitations and support motions are studied. The equations of motion, which represent two in-plane and two out-of-plane components, are solved using the method of multiple scales of order two considering the cases of primary external resonance and three simultaneous internal resonances. The effect of some control parameters is investigated [9]. The case of three-to-one internal resonance between the modes of the beam and the string in the presence of subharmonic resonance for the beam is considered and examined. The method of multiple scales is applied to study the steady-state response and the stability of the model. The effect of different parameters on the system is studied and several nonlinear behaviors of the system are found, which are confirmed numerically [10]. The dynamics of cable with concentrated loads were investigated using a direct perturbation method combined with multiple time scales. The model was assumed to have complex loads, including nonlinear aerodynamic force and concentrated masses [11]. The dynamic configuration of inextensible cables was studied [12]. Three components of displacement describing two equilibria of an extensible, traveling, elastic cable were obtained [13]. Simple formulas were established to analyze the global vibration of a cable-stayed bridge [14]. The global bifurcations of an inclined cable under external excitation with external damping are studied and the case of primary resonance is considered. The Shilinkov type homoclinic orbits and chaotic dynamics are analyzed using a new global perturbation technique [15]. The nonlinear dynamic responses of cable structures with two-to-one internal resonance cases [16-18], and three-to-one internal resonance [19] are studied using different methods and the chaotic dynamics of the cable model is illustrated by numerical simulations. Primary and subharmonic resonance cases in an inclined cable under external harmonic excitation are investigated theoretically and experimentally [20]. The present work examines the nonlinear resonant behavior of one in-plane mode that is coupled with two out-of-plane modes. The Galerkin method is used to discretize the governing nonlinear equation of motion into three ordinary differential equations with quadratic and cubic nonlinearities. Using the method of multiple scales, a set of first order nonlinear differential equations are obtained. The analytical results show that the system behavior includes several characteristics of the nonlinear system in the resonant frequency response curves. It is also shown that the system parameters have various effects on the nonlinear response of the considered model.
2. Cable Model Formulation
- The elastic cable of length L suspended between two supported ends, one is fixed and the second is vibrating support is shown in Fig. 1. The external excitation is assumed to be harmonic loading of the form f2(s)cosΩt acting upon the elastic cable in the tangential (in-plane) direction of the cable’s left support.
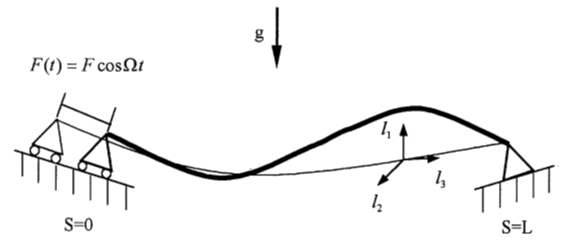 | Figure 1. Schematic diagram of the suspended elastic cable, [6] |
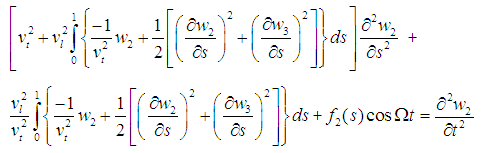 | (1) |
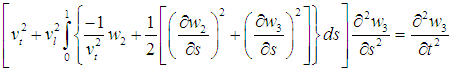 | (2) |
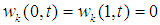 for k = 2,3.
for k = 2,3. 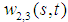 are nondimensional displacements with respect to the static equilibrium configuration of the cable in the normal and binormal directions, respectively, s is the nondimensional arc length coordinate of the cable and t is the nondiemnsional time.
are nondimensional displacements with respect to the static equilibrium configuration of the cable in the normal and binormal directions, respectively, s is the nondimensional arc length coordinate of the cable and t is the nondiemnsional time. 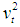 and
and 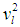 denote the nondimensional transverse and longitudinal wave speeds of the cable, respectively. The partial differential equations (1) and (2) are discretized considering one in-plane mode and two out-of plane modes using the following expansions, which represent separable solutions
denote the nondimensional transverse and longitudinal wave speeds of the cable, respectively. The partial differential equations (1) and (2) are discretized considering one in-plane mode and two out-of plane modes using the following expansions, which represent separable solutions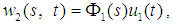 | (3) |
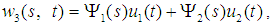 | (4) |
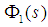 is the in-plane mode shape with the corresponding natural frequency ω1 and
is the in-plane mode shape with the corresponding natural frequency ω1 and 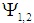 are out-of-plane mode shapes with the corresponding natural frequencies ω1,2. These mode shape functions are obtained by substituting Eqs. (3) and (4) into the linear equations of motion governing the free motion about the equilibrium position for normal and binormal directions, that are extracted from Eqs. (1) and (2). Then using separation of variables and applying the boundary conditions gives:
are out-of-plane mode shapes with the corresponding natural frequencies ω1,2. These mode shape functions are obtained by substituting Eqs. (3) and (4) into the linear equations of motion governing the free motion about the equilibrium position for normal and binormal directions, that are extracted from Eqs. (1) and (2). Then using separation of variables and applying the boundary conditions gives: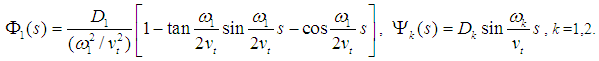 where D1 and Dk are arbitrary constants. Substituting Eqs. (3) and (4) into Eqs. (1) and (2), applying the applying the Galerkin method and adding linear viscous damping coefficients µ1,2,3 lead to the following three nonlinear coupled ordinary differential equations in terms of the nondimensional generalized coordinates u1,2,3(t):
where D1 and Dk are arbitrary constants. Substituting Eqs. (3) and (4) into Eqs. (1) and (2), applying the applying the Galerkin method and adding linear viscous damping coefficients µ1,2,3 lead to the following three nonlinear coupled ordinary differential equations in terms of the nondimensional generalized coordinates u1,2,3(t): 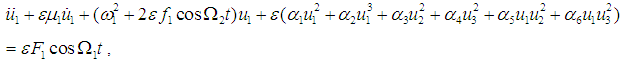 | (5) |
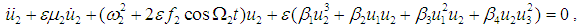 | (6) |
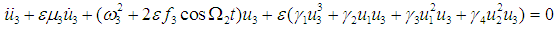 | (7) |
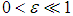 is a small perturbation parameter, F and Ω1 are the in-plane external forcing amplitude and frequencies, fj ( j =1,2,3) and Ω2 are parametric forcing amplitudes and frequency. These parameters are defined as follows
is a small perturbation parameter, F and Ω1 are the in-plane external forcing amplitude and frequencies, fj ( j =1,2,3) and Ω2 are parametric forcing amplitudes and frequency. These parameters are defined as follows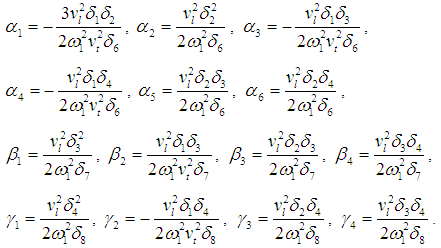 where
where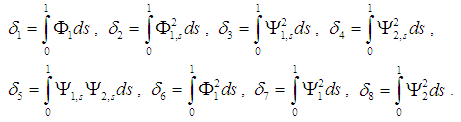
3. Perturbation Analysis
- A generalization of the method of multiple scales [21] is utilized to obtain a first-order uniform expansion for the solutions of Eqs. (5-7) in the form.
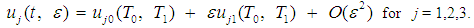 | (8) |
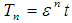 .Substituting Eq. (8) into Eqs. (5-7) and equating the coefficients of the same powers of ε , yield the followingOrder ε0:
.Substituting Eq. (8) into Eqs. (5-7) and equating the coefficients of the same powers of ε , yield the followingOrder ε0: 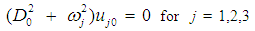 | (9) |
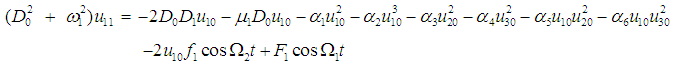 | (10) |
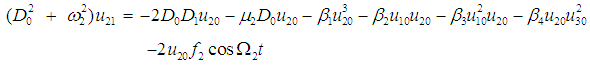 | (11) |
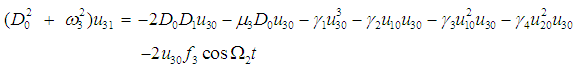 | (12) |
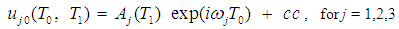 | (13) |
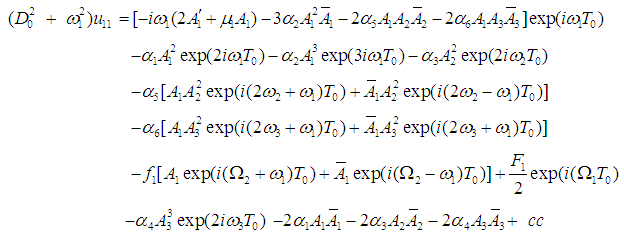 | (14) |
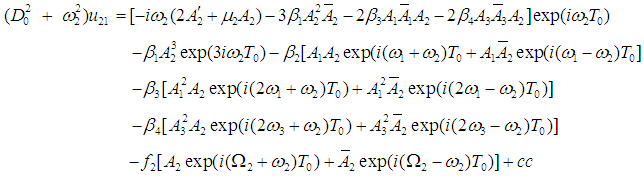 | (15) |
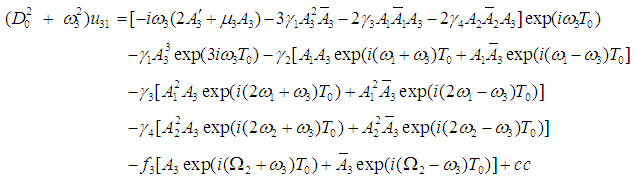 | (16) |
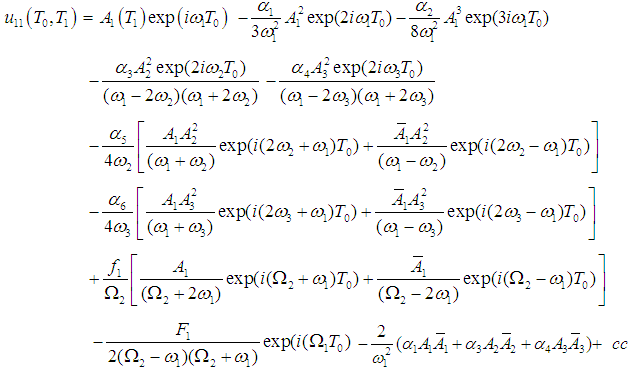 | (17) |
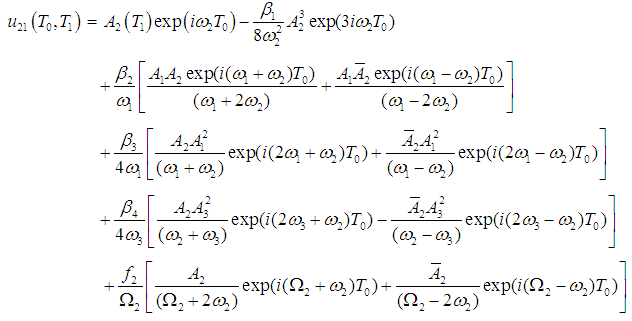 | (18) |
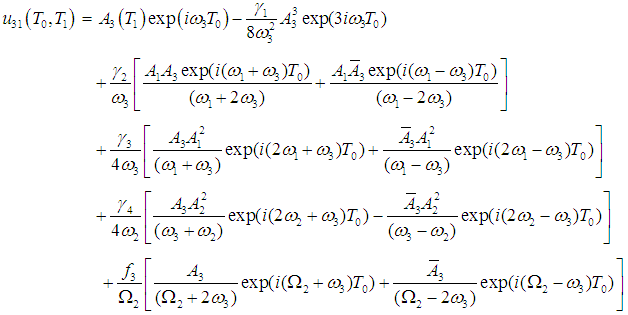 | (19) |
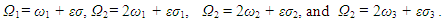 | (20) |
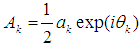 , k = 1,2,3, and the eliminating of the secular terms provides the following four equations governing the amplitude and phase modulations
, k = 1,2,3, and the eliminating of the secular terms provides the following four equations governing the amplitude and phase modulations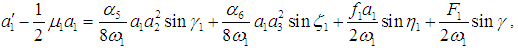 | (21) |
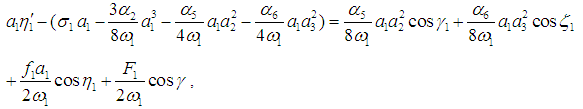 | (22) |
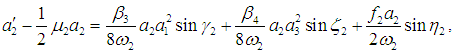 | (23) |
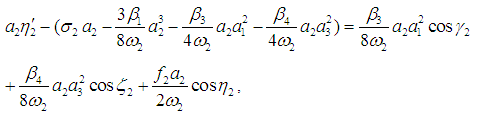 | (24) |
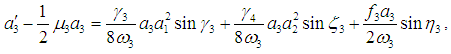 | (25) |
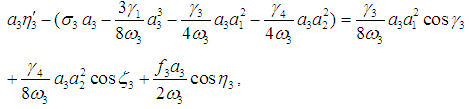 | (26) |
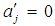 and
and 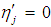 , for j = 1,2,3. Using these conditions in Eqs. (21-26) leads to
, for j = 1,2,3. Using these conditions in Eqs. (21-26) leads to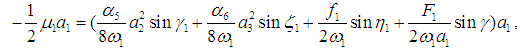 | (27) |
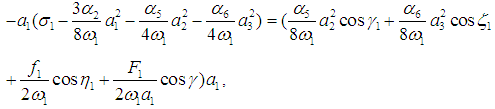 | (28) |
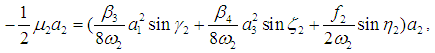 | (29) |
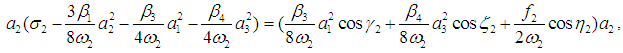 | (30) |
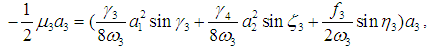 | (31) |
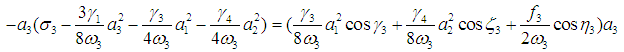 | (32) |
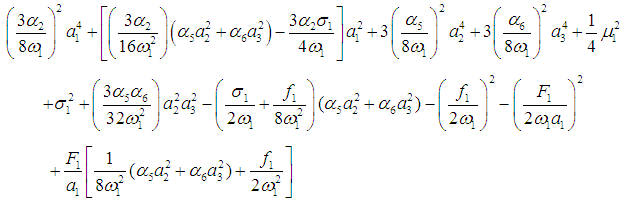 | (33) |
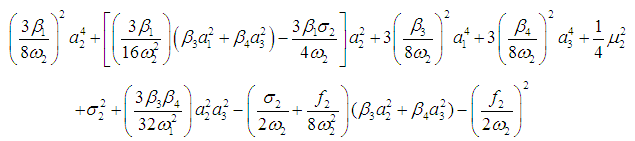 | (34) |
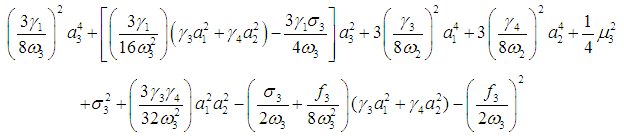 | (35) |
4. Numerical Results
- The steady-state periodic solutions corresponding to the fixed points of Eqs. (27-32) for simultaneous internal and principle parametric resonances of the three modes are obtained when the conditions
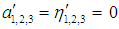 are implemented. From the resulting equations, the frequency response Eqs. (33-35) are obtained and solved numerically using the MAPLE© software. The analysis of local stability is determined by linearization of Eqs. (21-26) for the parameters a1,2,3 and η1,2,3 about each singular point, which will result in a set of linear equations with constant coefficients and hence lead to an eigen-value problem. Then, these eigen-values associated with the resulting linear equations will be examined. If the real part of every eigen-value of the coefficient matrix is positive then the point is unstable, otherwise must be stable. These linear equations are formed by assuming that each one of the parameters a1,2,3 and η1,2,3 is expressed in the form
are implemented. From the resulting equations, the frequency response Eqs. (33-35) are obtained and solved numerically using the MAPLE© software. The analysis of local stability is determined by linearization of Eqs. (21-26) for the parameters a1,2,3 and η1,2,3 about each singular point, which will result in a set of linear equations with constant coefficients and hence lead to an eigen-value problem. Then, these eigen-values associated with the resulting linear equations will be examined. If the real part of every eigen-value of the coefficient matrix is positive then the point is unstable, otherwise must be stable. These linear equations are formed by assuming that each one of the parameters a1,2,3 and η1,2,3 is expressed in the form 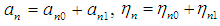 | (36) |
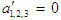 and
and 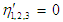 and an1 and ηn1 are small perturbations. Inserting Eq. (36) into Eqs. (21-26) and keeping the linear terms in an1 and ηn1, then solving the resulted the state-space equation
and an1 and ηn1 are small perturbations. Inserting Eq. (36) into Eqs. (21-26) and keeping the linear terms in an1 and ηn1, then solving the resulted the state-space equation 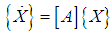 , where the matrix [A] is the Jacobian matrix, in order to calculate the eigen-values. The numerical results are presented in Figs. (2-5) as the steady-state amplitudes a1,2,3 are varied against the detuning parameters σ1,2,3 for different values of the system parameters. In these figures, Each curve consists of right and left branches. The left branch stands for the stable solutions and the right one stands for the unstable solutions. Considering Fig. (2a) as a basic case for comparison, where σ1 is plotted against a1 (in-plane mode). It can be seen from Figs. (2b) that as the linear viscous damping coefficient µ1 increases, the steady state amplitude of the first mode a1 decreases. Figures (2c) and (2d) show several representative curves for the cubic nonlinear term α2. Comparing these curves shows that the nonlinearity effect (either hardening or softening nonlinearity) bends the frequency response curves to right when α2 is positive and to left when α2 is negative. The figures also illustrate the variation of the steady-state amplitude as α2 is varied. The remaining cubic nonlinear terms α5 and α6, Figs. (2e, 2f), do not strongly change the amplitude as they are varied and hence no effect on the response curves. As the natural frequency ω1 increases, Fig. (2g), the branches of the response curves converge, and the region of unstable solutions decreases. The steady-state amplitude a1 is increased as the parametric excitation amplitude f1 increases as shown in Fig. (2h), whereas Fig. (2k) indicates that the variation of the external forcing amplitude F1 shows different effect and behavior on the frequency response curves. In Figs. (2i) and (2j), the resonant response curves are shifted to right as the steady-state amplitudes of the second and third modes a2 and a3 are increased.In addition, the force response curves presented in Fig. 3 illustrate the variations of the steady-state amplitude a1 with the forcing parametric excitation f1 for different values of the cubic nonlinear terms α2, α5 and α6. The significant effects of α5 and α6 are shown in Figs. (3c) and (3d), where the first mode amplitude increases as these nonlinear terms increase. For the second mode of vibration (first out-of-plane mode), the steady-state amplitude a2 is plotted against the detuning parameter σ2, as shown in Fig. (4). These curves illustrate the effects of the damping coefficient µ2, the cubic nonlinear terms β1,3,4, the natural frequency ω2, the parametric excitation amplitude f2, the steady-state amplitudes of the first and third modes a1 and a3. The force response curves of the second mode of vibration for different values of the damping term and nonlinear terms are shown in Fig. (5). It is noticed from Fig. (5b) that as the parametric excitation amplitude f2 increases beyond 25.0, the effect of increasing the linear damping coefficient µ2 becomes insignificant and the steady-state amplitude a2 of the first out-of-plane mode saturates. It is also noted that the curves are shifted to the right as µ2 is increased further, which means that the amplitude of the excitation f2 must exceed a critical value before the first out-of-plane amplitude a2 is to be strongly excited.Similar effects and curves are reported for the variation of the second out-of-plane amplitude a3 with σ1 and f3 for different values of system parameters, therefore they are not included in the figures.
, where the matrix [A] is the Jacobian matrix, in order to calculate the eigen-values. The numerical results are presented in Figs. (2-5) as the steady-state amplitudes a1,2,3 are varied against the detuning parameters σ1,2,3 for different values of the system parameters. In these figures, Each curve consists of right and left branches. The left branch stands for the stable solutions and the right one stands for the unstable solutions. Considering Fig. (2a) as a basic case for comparison, where σ1 is plotted against a1 (in-plane mode). It can be seen from Figs. (2b) that as the linear viscous damping coefficient µ1 increases, the steady state amplitude of the first mode a1 decreases. Figures (2c) and (2d) show several representative curves for the cubic nonlinear term α2. Comparing these curves shows that the nonlinearity effect (either hardening or softening nonlinearity) bends the frequency response curves to right when α2 is positive and to left when α2 is negative. The figures also illustrate the variation of the steady-state amplitude as α2 is varied. The remaining cubic nonlinear terms α5 and α6, Figs. (2e, 2f), do not strongly change the amplitude as they are varied and hence no effect on the response curves. As the natural frequency ω1 increases, Fig. (2g), the branches of the response curves converge, and the region of unstable solutions decreases. The steady-state amplitude a1 is increased as the parametric excitation amplitude f1 increases as shown in Fig. (2h), whereas Fig. (2k) indicates that the variation of the external forcing amplitude F1 shows different effect and behavior on the frequency response curves. In Figs. (2i) and (2j), the resonant response curves are shifted to right as the steady-state amplitudes of the second and third modes a2 and a3 are increased.In addition, the force response curves presented in Fig. 3 illustrate the variations of the steady-state amplitude a1 with the forcing parametric excitation f1 for different values of the cubic nonlinear terms α2, α5 and α6. The significant effects of α5 and α6 are shown in Figs. (3c) and (3d), where the first mode amplitude increases as these nonlinear terms increase. For the second mode of vibration (first out-of-plane mode), the steady-state amplitude a2 is plotted against the detuning parameter σ2, as shown in Fig. (4). These curves illustrate the effects of the damping coefficient µ2, the cubic nonlinear terms β1,3,4, the natural frequency ω2, the parametric excitation amplitude f2, the steady-state amplitudes of the first and third modes a1 and a3. The force response curves of the second mode of vibration for different values of the damping term and nonlinear terms are shown in Fig. (5). It is noticed from Fig. (5b) that as the parametric excitation amplitude f2 increases beyond 25.0, the effect of increasing the linear damping coefficient µ2 becomes insignificant and the steady-state amplitude a2 of the first out-of-plane mode saturates. It is also noted that the curves are shifted to the right as µ2 is increased further, which means that the amplitude of the excitation f2 must exceed a critical value before the first out-of-plane amplitude a2 is to be strongly excited.Similar effects and curves are reported for the variation of the second out-of-plane amplitude a3 with σ1 and f3 for different values of system parameters, therefore they are not included in the figures.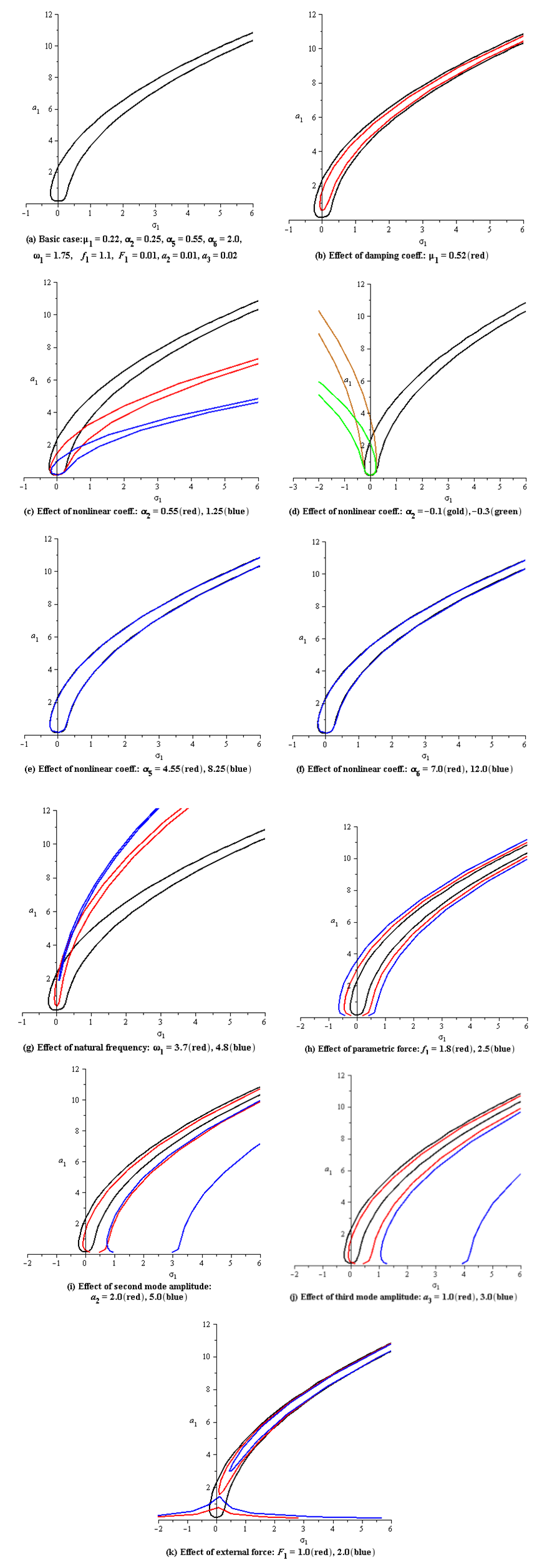 | Figure 2. Resonant frequency response curves for the first mode of the system |
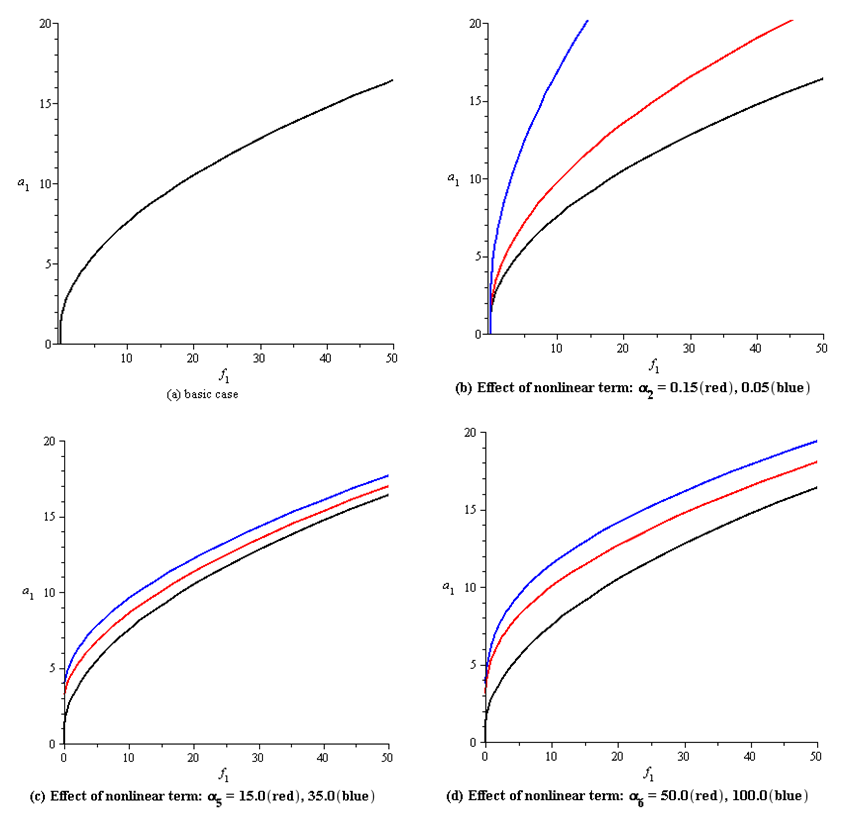 | Figure 3. Resonant force response curves for the first mode of the system |
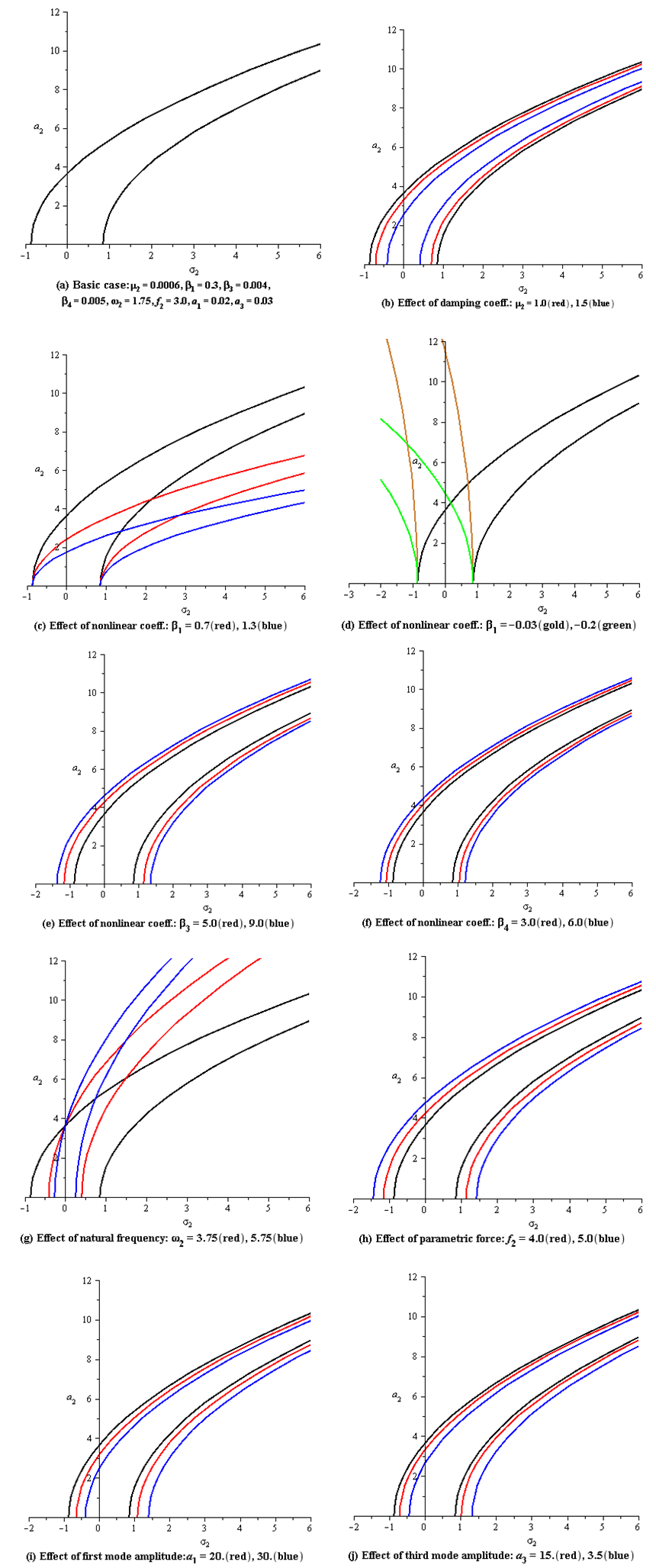 | Figure 4. Resonant frequency response curves for the second mode of the system |
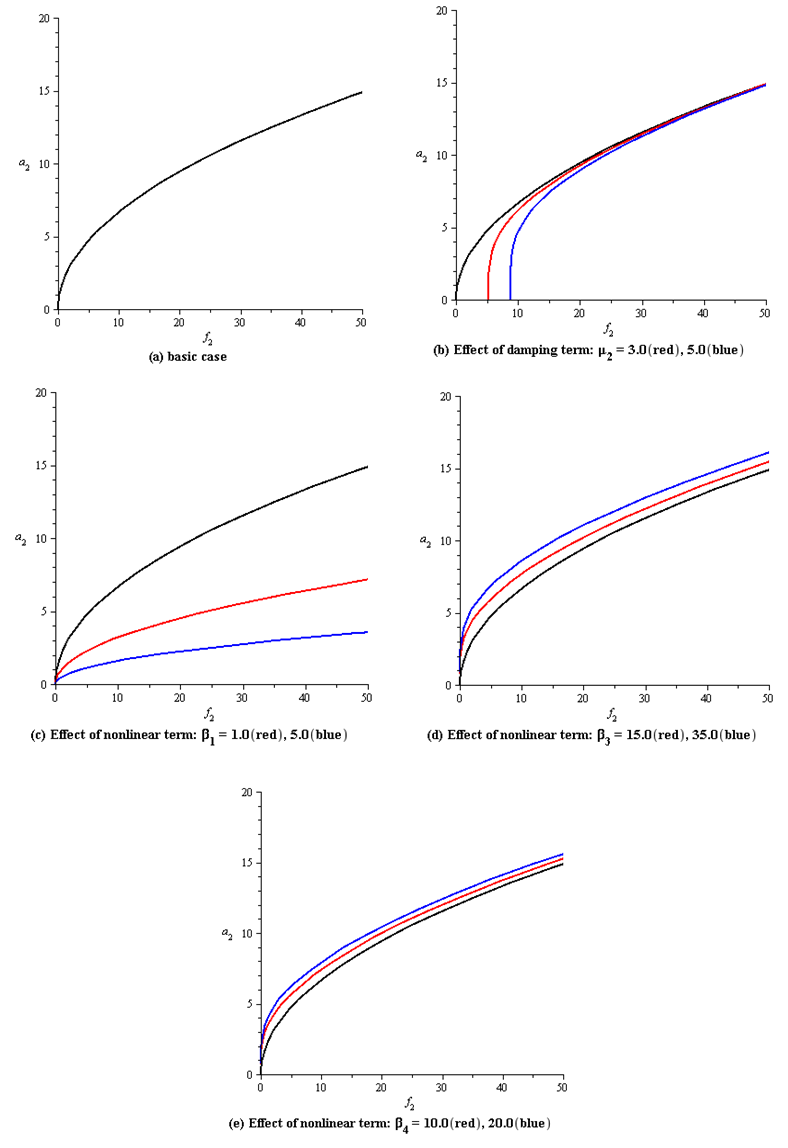 | Figure 5. Resonant force response curves for the second mode of the system |
5. Conclusions
- The nonlinear response of an elastic suspended cable to small tangential vibration of one support has been studied. The problem is described by a three-degree-of-freedom system of nonlinear ordinary differential equations, which represent one in-plane equation and two out-of-plane equations. The case of 1:1:1 internal resonance in the presence of principal parametric resonance between the in-plane and out-of-plane modes is studied by applying a perturbation method using a first-order approximation. The frequency response equation is numerically solved to obtain the steady-state solutions and to investigate the effects of different parameters on the system behavior.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML