P. N. Habu, F. Attah, H. Ibrahim
Department of Mathematics, Federal University Lafia, Lafia, Nigeria
Correspondence to: P. N. Habu, Department of Mathematics, Federal University Lafia, Lafia, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The motion of a fluid in an elastic tube when subjected to a pressure-gradient which is a periodic function of time is modeled and analyzed. This was done by considering the equations of the motion of the fluid and those of the motion of the tube. We obtained the average velocity across the tube and also a better approximation for the rate of flow was obtained.
Keywords:
Pressure-Gradient, Periodic function, Oscillatory motion, Thin-Walled elastic tube, Magnetic field
Cite this paper: P. N. Habu, F. Attah, H. Ibrahim, Oscillatory Motion of a Viscous Fluid in a Thin-Walled Elastic Tube with Induced Magnetic Field: A Proposed Therapy for Cancer and Hypertension Treatment, Applied Mathematics, Vol. 5 No. 5, 2015, pp. 97-100. doi: 10.5923/j.am.20150505.02.
1. Introduction
The problem of determining the motion of a liquid in an elastic tube when subjected to a pressure-gradient which is a periodic function of time, arises in connection with the flow of blood in the large arteries [1]. Performance modeling and analysis of blood flow in elastic arteries was investigated by G.C. Sharma et al. They estimated the effect of magnetic field on rheological model of blood. One of these models, is the Power-Low model and the other is generalized Maxwell model [2]. Thurston [8] attempted to study all of the rheological properties of blood with a model including non-Newtonian Viscosity, viscoelasticity and thixotropy.J. C. Misra and G. C. Shit studied the effect of magnetic field on blood flow through an artery, using a numerical model. Blood consisting of a suspension of red blood cells containing hemoglobin which contains iron oxide, it is quite apparent that blood is electrically conducting and exhibits magnetohydrodynamic flow characteristics [3]. P.N. Habu et al [12] and [13] investigated the effect of Magnetic Field in an Oscillatory flow and particle suspension in a fluid through an elastic tube:- An application to blood flow in arteries and also Oscillatory flow and particle suspension in a fluid through an elastic tube, respectively.Erica M. Cherry et al [4] studied Magnetic Drug Targeting Applications (MDTA) is a promising proposed technique for treating localized disease such as cancer [4]. In the present study, we investigated the Oscillatory motion of a viscous fluid in a thin-walled elastic tube with induced magnetic field. This can be considered as a proposed therapy for treating localized diseases such as cancer.The equations of motion of the tube are: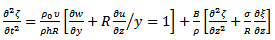 | (1) |
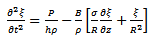 | (2) |
with the boundary conditions for the motion of the fluid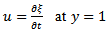 | (3) |
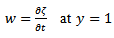 | (4) |
The equations of motion of the fluid are [12]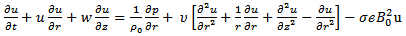 | (5) |
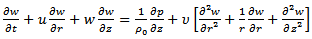 | (6) |
together with the continuity equation as 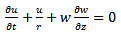 | (7) |
Since the fluid is subjected to a pressure-gradient which is a periodic function of time, we can make the following assumptions as in [12]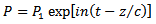 | (8) |
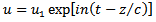 | (9) |
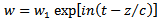 | (10) |
with the Womersley Number 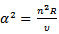 and
and 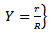 | (11) |
and 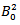 is a constants.Neglecting the inertia terms in eqn (5) and (6) and substitute (8) to (10) into (5) and (6) respectively, we obtain
is a constants.Neglecting the inertia terms in eqn (5) and (6) and substitute (8) to (10) into (5) and (6) respectively, we obtain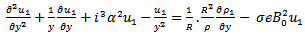 | (12) |
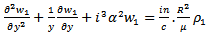 | (13) |
where 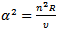 where the terms in
where the terms in 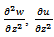 have been omitted, since
have been omitted, since 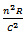 is small.Similarly, the equation of continuity (7) becomes
is small.Similarly, the equation of continuity (7) becomes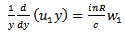 | (14) |
If now it is assumed that 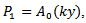 where k is to be determined, the equation of motion can be integrated as in [13], to give
where k is to be determined, the equation of motion can be integrated as in [13], to give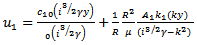 | (15) |
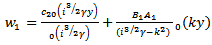 | (16) |
where 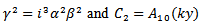
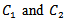 are arbitrary constants. If these values of
are arbitrary constants. If these values of 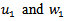 are inserted in the equation (7) it should reduce to an identity, i.e from (15) and (16), using (7), we get
are inserted in the equation (7) it should reduce to an identity, i.e from (15) and (16), using (7), we get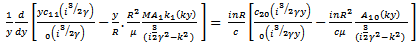
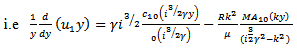 | (17) |
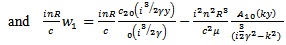 | (18) |
For the equation of continuity (14) to be satisfied, (17) and (18) must be identical, i.e 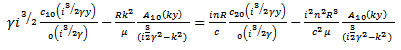 | (19) |
Using (19), equating coefficients of 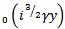 and
and 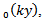 we obtain
we obtain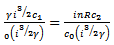 | (20) |
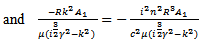 | (21) |
From (20) we have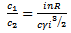 | (22) |
From (21) 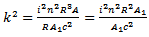
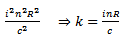 | (23) |
From [1] we use the approximations,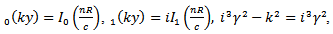
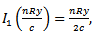 inserting these approximations into (15) and (16) we get
inserting these approximations into (15) and (16) we get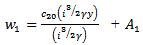 | (24) |
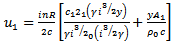 | (25) |
At the inner surface of the tube, i.e at 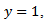
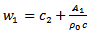 | (26) |
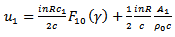 | (27) |
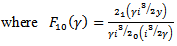 | (28) |
The value of 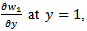 is also needed to be substituted in the equation of motion of the tube.Using eqn (16)
is also needed to be substituted in the equation of motion of the tube.Using eqn (16)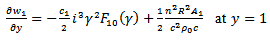 | (29) |
If it is now assumed that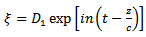 | (30) |
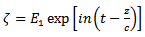 | (31) |
where 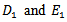 are arbitrary constants, the boundary condition for
are arbitrary constants, the boundary condition for 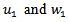 becomes
becomes 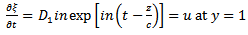 | (32) |
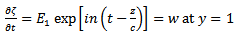 | (33) |
From eqn (32) and (33)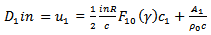 | (34) |
and similarly,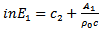 | (35) |
and the equation of motion of the tube can be written as 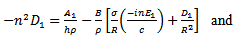 | (36) |
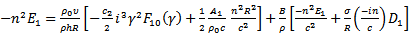 | (37) |
Eqns (34), (35), (36) and (37) are four homogeneous equations in the arbitrary constants 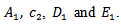 Eliminating them will give a “frequency equation” which will determine the wave-velocity, c, in terms of the elastic properties of the tube and the non-dimensional parameter
Eliminating them will give a “frequency equation” which will determine the wave-velocity, c, in terms of the elastic properties of the tube and the non-dimensional parameter 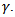 From [12], the result of the elimination will give
From [12], the result of the elimination will give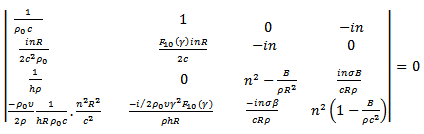 | (38) |
Operating on the columns and row of equation (38) several times we obtain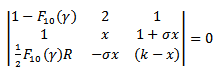 | (39) |
where 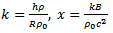 (39) becomes,
(39) becomes,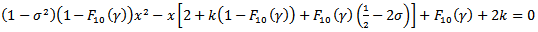 | (40) |
Hence the roots of (40) are given by [12]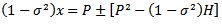 | (41) |
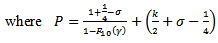 | (42) |
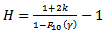 | (43) |
Now the details of the motion of the fluid at a particular value of Z, i.e over a short length of artery, will be studied. If the origin of Z is taken at the midpoint of this short length, the longitudinal velocity will be [1]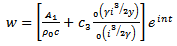 | (44) |
where the value of 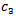 is to be determined from the boundary conditions. From (34), (35) and (36),
is to be determined from the boundary conditions. From (34), (35) and (36), 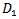 and
and 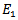 can be eliminated. If in the resulting equation,
can be eliminated. If in the resulting equation, 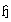 is written for the ratio of
is written for the ratio of 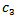 to
to  the value of
the value of 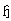 is given by [1]
is given by [1]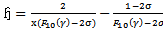 | (45) |
where 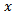 is the root of eqn (40), since
is the root of eqn (40), since 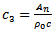 it follows that
it follows that 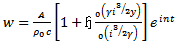 | (46) |
The first point to be noted is that for a given pressure-function, pressure gradient is inversely proportional to the wave-velocity, so that the velocity of the fluid and there the amount of flow, will be proportionately greater, in that which is more elastic.The constant 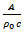 may be written as [1]
may be written as [1]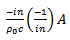 | (47) |
and since 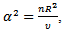 this may be written as
this may be written as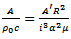 | (48) |
where 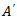 is the quantity that will be given by Fourier Analysis of the observed pressure-gradient. The average velocity across the tube is
is the quantity that will be given by Fourier Analysis of the observed pressure-gradient. The average velocity across the tube is 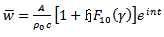 | (49) |
This can be put in the form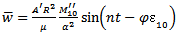 | (50) |
For a pressure-gradient 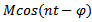 and the values of
and the values of 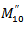 and
and 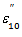 compared with those of
compared with those of 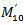 and
and 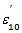 for the right tube. That is [1]
for the right tube. That is [1]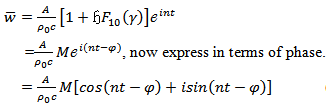 | (51) |
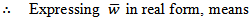
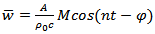 | (52) |
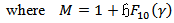 | (53) |
for 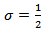 and
and 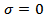
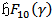 are; when
are; when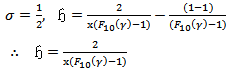 | (54) |
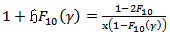 | (55) |
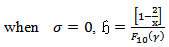 | (56) |
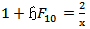 | (57) |
Using these formulae and the corresponding one for 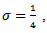 the values of
the values of 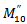 and
and 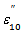 have been calculated by Womersley [1] for
have been calculated by Womersley [1] for 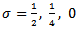 for the first four harmonics at the femoral artery. The formula for the rate of flow might at first sight be written as [1]
for the first four harmonics at the femoral artery. The formula for the rate of flow might at first sight be written as [1]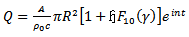 | (58) |
But this is only an approximation, since at any time the value of the radices is not R, but 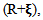 and varies with the time. Therefore we obtained the approximation as
and varies with the time. Therefore we obtained the approximation as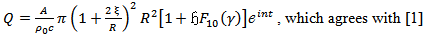 | (59) |
2. Conclusions
We have shown that the flow rate, 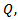 contains
contains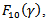 showing that
showing that 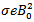 the applied magnetic field affects the flow rate. Also the longitudinal velocity, contains a function of
the applied magnetic field affects the flow rate. Also the longitudinal velocity, contains a function of 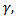 thereby pointing out that over a short length of the artery, the velocity is affected by the applied magnetic field. Magnetic Field Therapy (MFT) is one of the world’s oldest forms of healing. The first documented references to MFT in Medicine were made over 6,000 years ago (Google). For the study of Magnetic Field in the treatment of Cancer and hypertension, see [16] and [17] respectively. We therefore consider our model as a proposed therapy for Cancer and Hypertension treatment.
thereby pointing out that over a short length of the artery, the velocity is affected by the applied magnetic field. Magnetic Field Therapy (MFT) is one of the world’s oldest forms of healing. The first documented references to MFT in Medicine were made over 6,000 years ago (Google). For the study of Magnetic Field in the treatment of Cancer and hypertension, see [16] and [17] respectively. We therefore consider our model as a proposed therapy for Cancer and Hypertension treatment.
References
| [1] | J.R. Womersley; Oscillatory motion of viscous liquid in a Thin-Walled Elastic Tube-1: the linear approximation for long waves. Philos. Mag., Vol. 46, pp 199 (1955). |
| [2] | G.C. Sharma; M. Jain and A. Kumar, Performance Modelling and Analysis of blood flow in elastic arteries. Mathematical and Computer Modelling 39, (2004), 1491-1499. |
| [3] | J. C. Misra, G.C. Shit, Effect of Magnetic Field on Blood Flow through an artery:- A numerical model. TOM 12, Num.4, (2007). |
| [4] | Erica M. Cherry; John K. Eaton, Simulation of Magnetic particles in the bloodstream for magnetic Drug Targeting Applications. 8th International Conference on Multiphase Flow, ICMF 2013 Jeju, Korea. |
| [5] | Vardanyan. V.A. Effect of magnetic field on bloodflow, Biofizika 1973 Vol. 18 pp491-496. |
| [6] | Ling. S.C; Atabek H.B. A non-linear analysis of pulsatile flow in arteries. J. Fluid Mec 1972, Vol. 55 pp493-511. |
| [7] | Misra G.C; Pal B; Gupta A.S, Oscillatory entry flow in a plane channel with pulsating walls, Int.J. Non-Linear Mechanics 2001, Vol. 36 pp 731-741. |
| [8] | G.B. Thurston, Rheological parameter for the viscosity, visco-elasticity and thixotropy of blood, Biorheology 16, 149-155, (1979). |
| [9] | C.M. Rodkiewicz; P.Sinha and J.S. Kennedy, On the application of a constitive equation for whole human blood, J. of Biomechanical Engg. 112, 198-204 (1990). |
| [10] | A. Dutta and J.M. Tarbell, Influence of a non-Newtonian behavior of blood flow in an elastic artery model. ASME J. of Biomechanical Engg. 118, 111-119 (1996). |
| [11] | A. Dutta, D.M Wang and J.M. Tarbell, Numerical analysis of flow in an elastic artery model, ASME J. of Biomechanical Engg. 114, 26-32 (1992). |
| [12] | P.N Habu, I.G. Bassi and F. Attah, Effect of Magnetic Field in an Oscillatory Flow and particle Suspension in a Fluid Through an Elastic Tube:- An Application to Blood Flow in Arteries. American Journal of Mathematics and Statistics, 2015, 5(5): 306-310. |
| [13] | P.N. Habu, M.A. Mbah, Oscillatory Flow and Particle Suspension in a Fluid through an Elastic Tube. Journal of Mathematical Theory and Modeling, 2013, Vol. 3 num 11, p 109- 114. |
| [14] | Taylor. M. G. Wave travel in arteries and the design of the cardiovascular system. McGraw-Hill Book Company, New York (1964) pp343-372. |
| [15] | Spiegel. M.R (1980), Advanced Mathematics for Engineers and Scientists. McGraw-Hill Company, New York, p 352-353. |
| [16] | Anusheel Varshney and Gautan Kumar, Effects of Magnetic Field on Cancer Cell line, Journal of Experimental Biology and Agricultural Sciences, ISSN No 2320-8694, June 2013, Vol 1(25). |
| [17] | Hideyuki Okano and Chiyaji Ohkubo, Anti-Pressor effects of whole body exposure to static magnetic field on pharmacologically induced hypertension in conscious rabbits, Bioelectromagnettics, Vol 24, Issue 2, page 139-147, February 2013. |


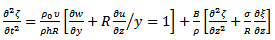
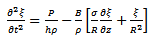
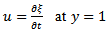
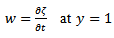
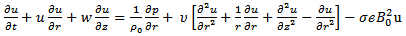
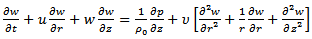
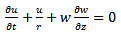
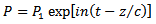
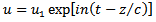
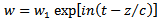
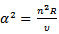 and
and 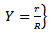
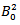 is a constants.Neglecting the inertia terms in eqn (5) and (6) and substitute (8) to (10) into (5) and (6) respectively, we obtain
is a constants.Neglecting the inertia terms in eqn (5) and (6) and substitute (8) to (10) into (5) and (6) respectively, we obtain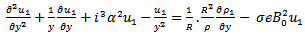
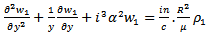
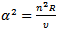 where the terms in
where the terms in 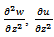 have been omitted, since
have been omitted, since 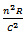 is small.Similarly, the equation of continuity (7) becomes
is small.Similarly, the equation of continuity (7) becomes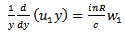
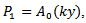 where k is to be determined, the equation of motion can be integrated as in [13], to give
where k is to be determined, the equation of motion can be integrated as in [13], to give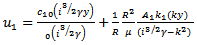
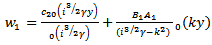
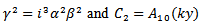
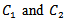 are arbitrary constants. If these values of
are arbitrary constants. If these values of 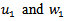 are inserted in the equation (7) it should reduce to an identity, i.e from (15) and (16), using (7), we get
are inserted in the equation (7) it should reduce to an identity, i.e from (15) and (16), using (7), we get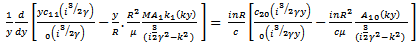
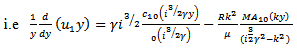
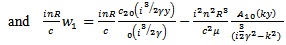
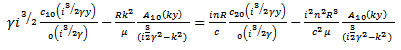
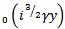 and
and 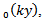 we obtain
we obtain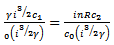
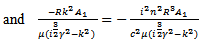
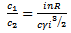
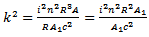
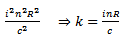
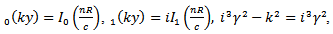
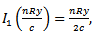 inserting these approximations into (15) and (16) we get
inserting these approximations into (15) and (16) we get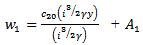
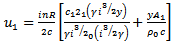
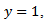
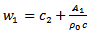
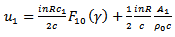
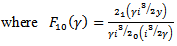
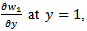 is also needed to be substituted in the equation of motion of the tube.Using eqn (16)
is also needed to be substituted in the equation of motion of the tube.Using eqn (16)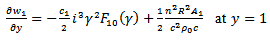
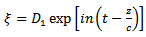
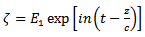
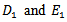 are arbitrary constants, the boundary condition for
are arbitrary constants, the boundary condition for 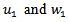 becomes
becomes 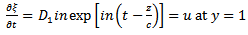
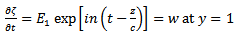
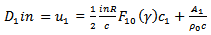
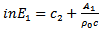
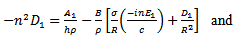
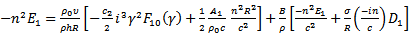
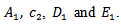 Eliminating them will give a “frequency equation” which will determine the wave-velocity, c, in terms of the elastic properties of the tube and the non-dimensional parameter
Eliminating them will give a “frequency equation” which will determine the wave-velocity, c, in terms of the elastic properties of the tube and the non-dimensional parameter  From [12], the result of the elimination will give
From [12], the result of the elimination will give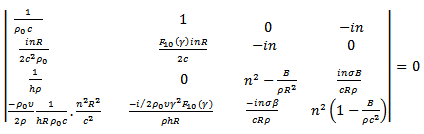
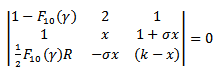
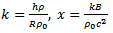 (39) becomes,
(39) becomes,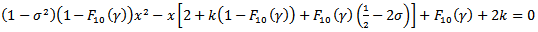
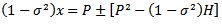
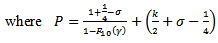
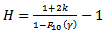
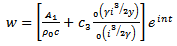
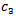 is to be determined from the boundary conditions. From (34), (35) and (36),
is to be determined from the boundary conditions. From (34), (35) and (36), 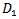 and
and 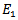 can be eliminated. If in the resulting equation,
can be eliminated. If in the resulting equation, 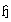 is written for the ratio of
is written for the ratio of 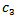 to
to  the value of
the value of 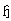 is given by [1]
is given by [1]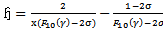
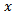 is the root of eqn (40), since
is the root of eqn (40), since 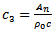 it follows that
it follows that 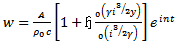
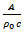 may be written as [1]
may be written as [1]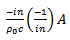
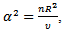 this may be written as
this may be written as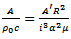
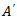 is the quantity that will be given by Fourier Analysis of the observed pressure-gradient. The average velocity across the tube is
is the quantity that will be given by Fourier Analysis of the observed pressure-gradient. The average velocity across the tube is 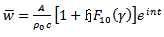
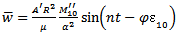
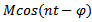 and the values of
and the values of 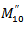 and
and 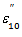 compared with those of
compared with those of 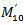 and
and 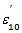 for the right tube. That is [1]
for the right tube. That is [1]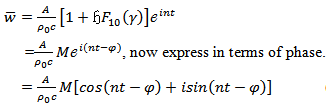
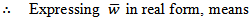
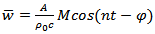
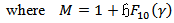
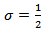 and
and 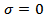
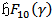 are; when
are; when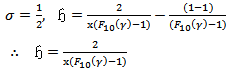
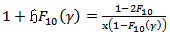
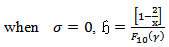
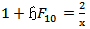
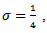 the values of
the values of 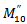 and
and 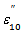 have been calculated by Womersley [1] for
have been calculated by Womersley [1] for 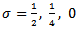 for the first four harmonics at the femoral artery. The formula for the rate of flow might at first sight be written as [1]
for the first four harmonics at the femoral artery. The formula for the rate of flow might at first sight be written as [1]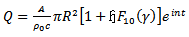
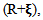 and varies with the time. Therefore we obtained the approximation as
and varies with the time. Therefore we obtained the approximation as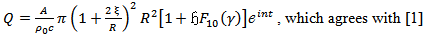
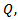 contains
contains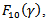 showing that
showing that 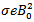 the applied magnetic field affects the flow rate. Also the longitudinal velocity, contains a function of
the applied magnetic field affects the flow rate. Also the longitudinal velocity, contains a function of 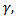 thereby pointing out that over a short length of the artery, the velocity is affected by the applied magnetic field. Magnetic Field Therapy (MFT) is one of the world’s oldest forms of healing. The first documented references to MFT in Medicine were made over 6,000 years ago (Google). For the study of Magnetic Field in the treatment of Cancer and hypertension, see [16] and [17] respectively. We therefore consider our model as a proposed therapy for Cancer and Hypertension treatment.
thereby pointing out that over a short length of the artery, the velocity is affected by the applied magnetic field. Magnetic Field Therapy (MFT) is one of the world’s oldest forms of healing. The first documented references to MFT in Medicine were made over 6,000 years ago (Google). For the study of Magnetic Field in the treatment of Cancer and hypertension, see [16] and [17] respectively. We therefore consider our model as a proposed therapy for Cancer and Hypertension treatment. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML