-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2015; 5(5): 93-96
doi:10.5923/j.am.20150505.01

Computing the Hosoya Polynomial, Wiener Index and Hyper-Wiener Index of the Harary Graph
Mohammad Reza Farahani1, M. R. Rajesh Kanna2
1Department of Applied Mathematics of Iran University of Science and Technology (IUST), Narmak, Tehran, Iran
2Post Graduate Departments of Mathematics, Maharani's Science College for Women, Mysore, India
Correspondence to: Mohammad Reza Farahani, Department of Applied Mathematics of Iran University of Science and Technology (IUST), Narmak, Tehran, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The distance d(u,v) between two vertices u and v of a connected graph G is equal to the length of a shortest path that connects u and v. The Hosoya polynomial was introduced by H. Hosoya in 1988 and defined as H(G,x)= ½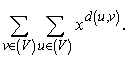 Also, the Wiener index W(G) is the sum of all distances between vertices of G as W(G)=½
Also, the Wiener index W(G) is the sum of all distances between vertices of G as W(G)=½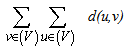 whereas the hyper-Wiener index WW(G) is defined as
whereas the hyper-Wiener index WW(G) is defined as 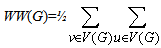 (d(u,v)+d(u,v)2). In this paper, we compute the Hosoya polynomial of the Harary graph. Also we compute the Wiener index and hyper Wiener index of this family of Regular graphs.
(d(u,v)+d(u,v)2). In this paper, we compute the Hosoya polynomial of the Harary graph. Also we compute the Wiener index and hyper Wiener index of this family of Regular graphs.
Keywords: Harary graph, Topological Indices, Hosoya polynomial, Wiener Index, Hyper-Wiener index
Cite this paper: Mohammad Reza Farahani, M. R. Rajesh Kanna, Computing the Hosoya Polynomial, Wiener Index and Hyper-Wiener Index of the Harary Graph, Applied Mathematics, Vol. 5 No. 5, 2015, pp. 93-96. doi: 10.5923/j.am.20150505.01.
1. Introduction
- Let G=(V,E) be a simple connected graph. The vertex-set and edge-set of G denoted by V=V(G) and E=E(G), respectively. An edge e=uv of a graph G is joined between two vertices u and v. The distance between vertices u and v, d(u,v), in a graph is the number of edges in a shortest path connecting them and the diameter of a graph G, D(G) is the longest topological distance in G.A topological index of a graph is a single unique number characteristic of the graph and is mathematically invariant under graph automorphism. The topological index of a molecular graph G is a non-empirical numerical quantity that quantifies the structure and the branching pattern of G. Usage of topological indices in biology and chemistry began in 1947 when H. Wiener [1, 2] introduced Wiener index to demonstrate correlations between physicochemical properties of organic compounds and the index of their molecular graphs.The hyper-Wiener index is one of distance-based graph invariants, (based structure descriptors), used for predicting physico–chemical properties of organic compounds. The hyper-Wiener index was introduced by M. Randić in 1993 [3, 4]. The Wiener index and the hyper Wiener index of G are defined as follows:
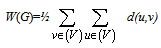 | (1) |
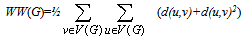 | (2) |
 | (3) |
2. Main Result
- The aim of this section is to obtain a closed formula of Hosoya polynomial, Wiener index and hyper-Wiener index of the Harary graph H2r+1,2n. At first we need the following definition.Definition 1 [21-24]. Let r and n be two positive integer numbers and n≥r+1, then in the Harary graph H2r+1,2n, two vertices i and j are joined if and only if | i-j|≤ r or j=i+n (∀i,j∊ℤ2n).Example 1. In case r=2 and n=6 (6≥2+1), the Harary graph H5,12 is shown in Figure 1. By Definition 1, one can see that the vertex v1 is joined with the vertices v2,v3, v12,v11 and v7, since 7-1=6 and for all numbers 2,3,11 and 12 (∊ℤ12), |1-2|=|1-12|<|1-3|=|1-11|≤2.
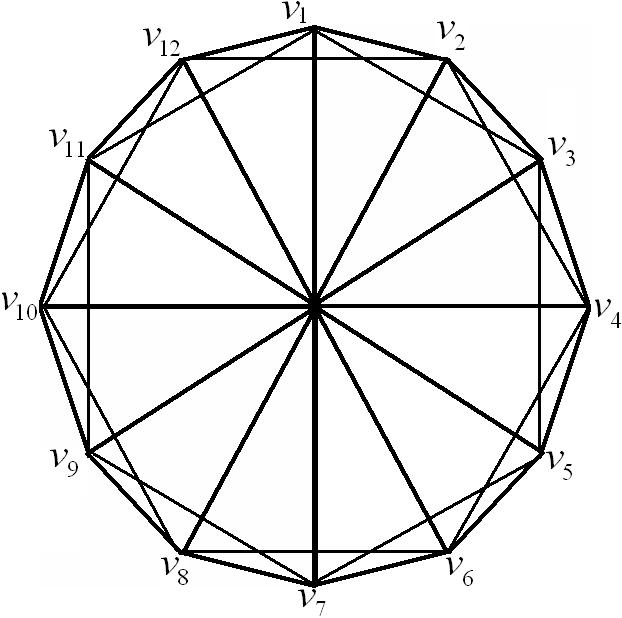 | Figure 1. The Harary graph H5,12 |
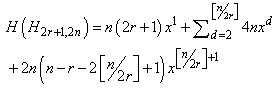 | (4) |
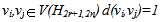 if and only if i−r ≤ j ≤ i+r or |j-i|=n (∀i,j=1,2,…,n), thus the coefficient of the first term in the Hosoya polynomial of G ( x1 ) is equal to |E(H2r+1,2n)|=2rn+n.On the other hand from the structure of H2r+1,2n, ∀i,j∊ℤ2n & |i-j|≤r or |i-j|=n d(vi,vi±(r+j))= d(vi,vi+n±j)=2, since for a vertex vi∊V(H2r+1,2n), vi,vj, vi,vi±r, vi,vi+n, vi±rvi±r+j and vi+n,vi+n±j belong to E(H2r+1,2n). Hence the coefficient of the second term in H(H2r+1,2n,x) is 4n.Also by similar argument, one can see that for all vertices of G, d(vi,vi±(dr+j)) and d(vi,vi+n±((d-1)r+j)) are equal to d+1, where
if and only if i−r ≤ j ≤ i+r or |j-i|=n (∀i,j=1,2,…,n), thus the coefficient of the first term in the Hosoya polynomial of G ( x1 ) is equal to |E(H2r+1,2n)|=2rn+n.On the other hand from the structure of H2r+1,2n, ∀i,j∊ℤ2n & |i-j|≤r or |i-j|=n d(vi,vi±(r+j))= d(vi,vi+n±j)=2, since for a vertex vi∊V(H2r+1,2n), vi,vj, vi,vi±r, vi,vi+n, vi±rvi±r+j and vi+n,vi+n±j belong to E(H2r+1,2n). Hence the coefficient of the second term in H(H2r+1,2n,x) is 4n.Also by similar argument, one can see that for all vertices of G, d(vi,vi±(dr+j)) and d(vi,vi+n±((d-1)r+j)) are equal to d+1, where 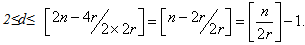 This implies that the diameter of Harary graph H2r+1,2n will be
This implies that the diameter of Harary graph H2r+1,2n will be 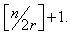 It is easy to see that the latest coefficient in H(H2r+1,2n,x) is equal to
It is easy to see that the latest coefficient in H(H2r+1,2n,x) is equal to 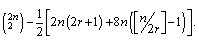 Therefore by using the definition of Hosoya polynomial, we have
Therefore by using the definition of Hosoya polynomial, we have 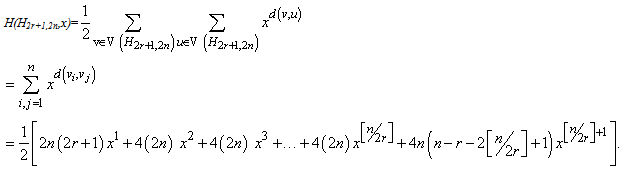 And this complete the proof of Theorem 1.According to Equation 3, we can obtain the Wiener index and the hyper-Wiener index of the Harary graph H2r+1,2n by the Hosoya polynomial.Theorem 2. Let H2r+1,2n be the Harary graph (∀r,n∊ℤ & n≥r+1). Then, the Wiener index of H2r+1,2n is equal to
And this complete the proof of Theorem 1.According to Equation 3, we can obtain the Wiener index and the hyper-Wiener index of the Harary graph H2r+1,2n by the Hosoya polynomial.Theorem 2. Let H2r+1,2n be the Harary graph (∀r,n∊ℤ & n≥r+1). Then, the Wiener index of H2r+1,2n is equal to 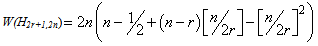 Proof. Consider the Harary graph G= H2r+1,2n. From definitions of the Wiener index and Hosoya Polynomial of G (Equations 1 and 3), we see that the Wiener index W(G) is the first derivative of the Hosoya polynomial H(G,x) evaluated at x=1. Thus
Proof. Consider the Harary graph G= H2r+1,2n. From definitions of the Wiener index and Hosoya Polynomial of G (Equations 1 and 3), we see that the Wiener index W(G) is the first derivative of the Hosoya polynomial H(G,x) evaluated at x=1. Thus 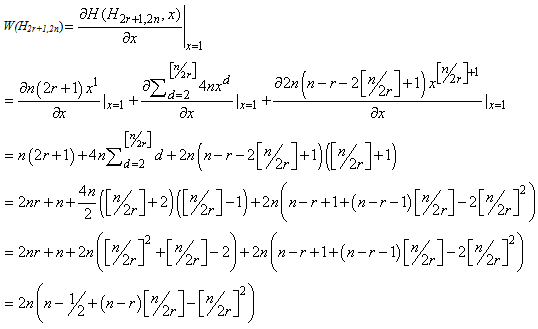 Here the proof of Theorem 2 is completed. As an immediately result from Theorem 2, we have.Theorem 3. For given positive integer numbers r and n (n≥r+1), the hyper-Wiener index of the Harary graph H2r+1,2n is equal to
Here the proof of Theorem 2 is completed. As an immediately result from Theorem 2, we have.Theorem 3. For given positive integer numbers r and n (n≥r+1), the hyper-Wiener index of the Harary graph H2r+1,2n is equal to 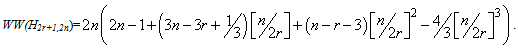 Proof. Let H2r+1,2n be the Harary graph (∀r,n∊ℤ & n≥r+1) . According to Equation 2, we can compute the hyper-Wiener index of H2r+1,2n as follows:
Proof. Let H2r+1,2n be the Harary graph (∀r,n∊ℤ & n≥r+1) . According to Equation 2, we can compute the hyper-Wiener index of H2r+1,2n as follows: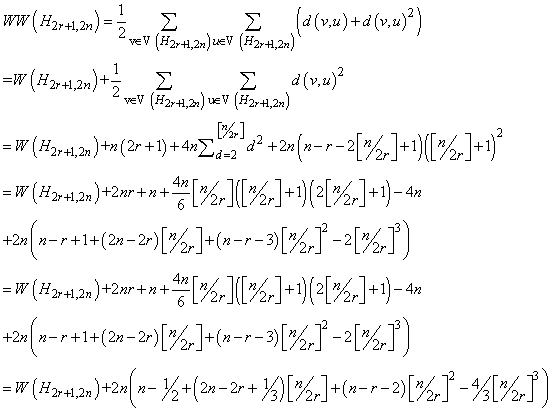
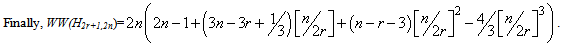
ACKNOWLEDGEMENTS
- Authors are also thankful to the University Grants Commission, Government of India, for the financial support under the GrantMRP(S)-0535/13-14/KAMY004/UGC-SWRO.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML