1. Introduction

Bisection of plane geometric angles is the only procedure taught for the division of angles in introductory plane geometry and there are text books [1-5] dealing on this subject matter. This routine method has continued to dominate the scene despite the fact that it divides angles only into 2, 4, 8 etc excluding 3, 5, 6, 7, 9 etc equal parts. This could be caused by the absence of other simple methods or that some angles that cannot be obtained through bisection can be copied from the protractor or the use of set squares. The method by Givens [6] is mathematically complex, tedious and cannot be practiced by High School students. There is therefore the need for other methods to be introduced. The main aim of this article is to introduce other methods that equally partition any plane angle into a number of parts and in addition to highlight some other applications of the result of these methods.

2. Methodology

2.1. Basic Principles of the New Methods

The new methods utilize the following principles of plane geometry. The arc length l of arc AB of a sector AOB (or circle) of radius r subtends a definite angle θ^o at the centre O, figure 1. Also at constant angle θ^o the arc length l of AB increases in the same proportion as the radius increases. Follow up of these are that for the concentric arcs AB (radius r) and arc CD (radius 2r), figure 1, arc length CD is twice arc length AB. All these are derivable from the equation arc length l = 2πrθ/360.

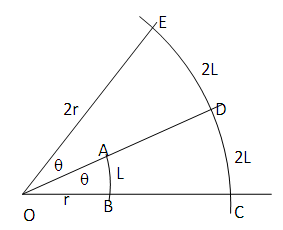Figure 1. Relationship between θ, arc length and radius

If arc length CD, figure 2, is partitioned into three equal parts say, each one third arc length CE, EF, FD will subtend θ/3. Therefore to divide a sector angle into n equal parts, the sector arc will be divided into n equal parts. The difficulty in dividing arc length into any number of equal parts is overcome in two ways. One way is by applying the direct relationship between arc length and its radius. The second approach is by direct sectioning of the arc length through estimation followed by exact division. These pathways are explained below.

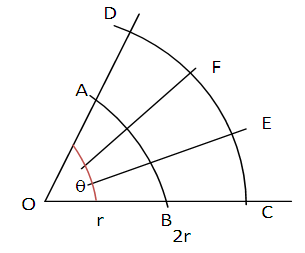Figure 2. Relationship between arc length and radius

2.2. Partitioning of Arc Length of an Angle

(a). Applying direct variation of Arc Length with its Radius

As arc length increases in direct proportion as its radius, the radius R of the sector will be divided into n equal parts so R equals nr and r is the radius of the least concentric arc.

The sector arc can now be partitioned into n parts by dividing it by the arc length of the smallest arc. Each of the small arcs from the division will subtend at the center θ°/n. In practice it is found that it is better to use half (or twice this half) the arc length of the least arc. So the sector angle or the least arc is bisected. The detailed steps are as listed in section 2.2a.

2.2a Equal Division of Angle applying direct variation of Arc Length with its Radius: Procedure

To divide an angle, say 60^o into five equal parts.

a) Draw or construct ∠POQ = 60°, figure 3.

b) From O with any convenient radius cut along OQ such that OC = CD = DE = EF = FB.

c) O as centre, radius OC swing arc CG and O as centre and radius OB swing arc BA. The angle is converted to a sector AOB.

d) Let OR be the bisector of angle AOB.

e) B as starting point divide arc BA by arc lengths CH + HG

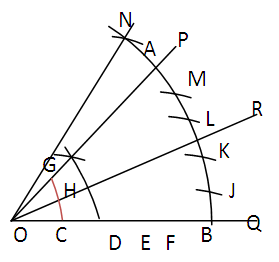Figure 3. Equal division of an angle, say 60°, into five parts

(i.e. chord CH + chord HG not chord CG) into BJ, JK, KL, LM and MA. Arc AB is divided into five equal parts so also the sector AOB into five equal small sectors each with sector angle equal to 60°/5 i.e. 12°. Dividing arc AB by arc CH gives ten parts to be paired.

(b) Applying Approximate Partitioning followed by Actual Division, Second Method

In this process, the arc is sectioned into n parts of which n-1 parts are equal and the last may differ. With pair of compasses the chord lengths of each of these small arcs are transferred to a straight line and the sum divided by n directly or by the parallel line method. The quotient is used to accurately divide the sector arc. Details of this procedure are given in section 2.2b.

2.2b Equal Division of Angle applying Approximate Partitioning followed by Actual Division: Procedure for say 60° into three equal parts (n=3).

a) Draw or construct the angle POQ giving it long arms (sides) so as to have long arc when converted to a sector, figure 4.

b) O as centre with long enough radius swing arc AB. The angle is turned to a sector figure 4a.

c) Using a pair of compasses and a convenient radius cut arc AB at c and d i.e. Ac = cd; dB may or may not be equal to cd.

d) On a straight line, figure 4b, mark the point A. A as centre, figure 4b, and radius same as in (c) above, cut Ac = cd. With d on the straight line as centre and radius dB on the arc AB cut point B on the straight line. Draw AJ at any convenient angle and with any convenient radius mark off AK = KL = LM. Join MB and draw a line through L parallel to MB to meet AB figure 4b at D.

e) With A (on the sector) as centre and radius DB (on the straight line) cut sector arc AB at C and D. Arc AC = CD = DB so also chord AC = CD = DB. Hence the sector angle θ is trisected by completing the three component sectors.

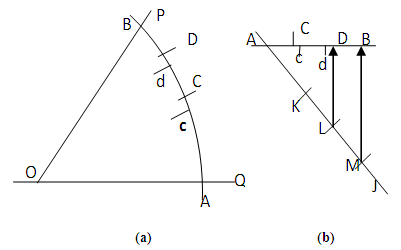Figure 4. Trisection of 60o by the second Method

2.3. Other Applications of the New Method

Givens [6] in his paper observed that angle trisection and in fact division of angles into equal number of parts is of very great importance because of the wider use which may be made of the knowledge. Here under are some of the applications. Once an angle is divided into a number of equal parts, new angles can be constructed either by adding or subtracting one part of the quotient as illustrated below. An angle can also be divided into a ratio. In most cases a simple arithmetic, as shown in 2.3.1 to 2.3.3, is needed. Calculations for some other angles are shown in Table 1.

2.3.1. To Construct 72°

Needed calculation is: 72 = 60 + 12 = 60 + 60/5.

So construct or draw angle 60° figure 3, divide it into five equal parts as in 2.2a,b and add a sector of 12° to sector of angle 60°. The addition goes thus: A as centre, radius AM cut arc BA produced at N, ∠NOB = 72°.

2.3.2. To Construct Angle 48^o

Similarly 48 = 60 – 12 = 60 - 60/5.

This means discarding the ∠BOJ or ∠AOM = 12° sector, figure 3. Discarding ∠AOM leaves ∠MOB = 48°.

2.3.3. To divide an Angle into a Given Ratio e.g. 2:3.

Sum of ratio is five.

Still on figure 3 as example, the angle is divided into five. Combining the last two sectors each of 12° gives a sector AOL of 24°; the first three sectors form a sector BOL of angle 36°. The ratio is 2:3.

3. Results and Discussion

3.1. Basic Principles of the New Methods

The direct proportionality of arc length to radius at constant angle and of arc length to angle at constant radius are known facts in plane geometry. Therefore the sector arc length will increase integrally as the radius integrally increases. The division of the radius of the sector into equal parts is to have any arc length with any of these radii a multiple of the length of the least arc. This makes it possible to divide the sector arc into the desired number of small arcs and also the sector angle into the desired number of parts. The length of any arc having any of these radii and is concentric with the sector arc will be an integral multiple of the least arc. Arc lengths of succeeding arcs will thus increase as multiples of the least arc length. The divisor CH (or CH + HG) is the chord of the arc CH (or CH and HG) and not half of chord CG. Also the sum of chord CH and chord HG is greater than chord CG. When bisected, it is chords CH and HG (actually the arcs) that subtend equal angles at O. Fig 5 shows that chords CE + ED (arcs CE + ED) not chord COD equals chord BF (or arc BF). The line bisector of the sector angle not only provides the divisor but also acts as a check to know whether the centre of each arc lies on it.

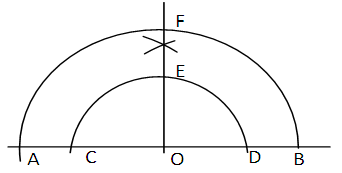Figure 5. Bisection of angle 180o by the new method

The second procedure utilizes the additional fact that averaging gives the length for each n different lengths that should be equal. The different lengths of chords of these nearly equal arcs become equal when averaged to give the required equal length. The second method is suitable for partitioning both small and large angles. The division of angle applying direct variation of arc length with its radius is similar to equal division of a straight line by the parallel line method [7, 8] as shown in figure 6.

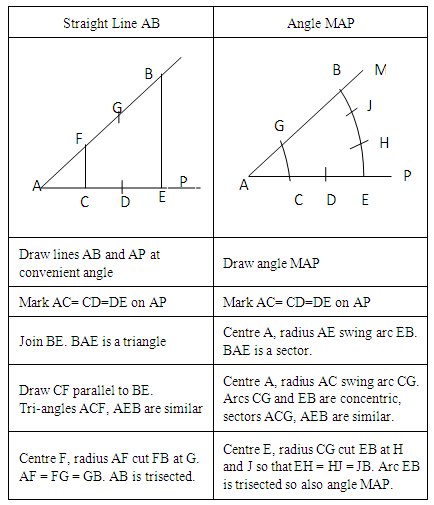Figure 6. Comparison of Equal Division (e.g. trisection) of a Straight Line and also an Angle

3.2. Other Applications of the New Methods

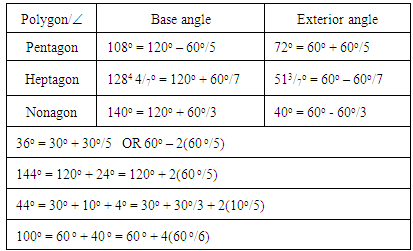
The construction of angles by the new methods through the addition or subtraction procedure is straight forward and must be carried out in a sector of same radius since it is a section of the arc length of the main sector that is involved. A change in radius gives wrong result. Addition and subtraction of angles and also division of angles into ratio parts are possible in bisection method but the angle(s) to be added or subtracted or expressed as ratio parts are those angles that can be obtained from bisection. For example 75° = 60° + 15°. 15° can be obtained from bisecting 60^o and the resulting 30°. Splitting 60° into 20° and 40° (i.e. 1:2 ratio) is not possible through bisection as neither 20° nor 40° can be constructed by bisection unless by the equipartition procedures.

The new methods coupled with the routine method of constructing and bisecting angles make it possible to construct such angles like 10°, 12°, 40°, 72°, 108° to mention a few. By combining the routine method with the new methods regular polygons of base angles 108°, (exterior angle 72°) and 128⁴4/₇^o (exterior angle 51³/₇^o) and others, see Table 1, can be constructed if the length of its side is known and the base angle or the exterior angle can be easily constructed.

Table 1. Essential Calculations for Angles of some Regular Polygons and some other Angles

4. Conclusions

The new procedures are easy and versatile and when coupled with existing routine methods more difficult constructions can be done. The new methods should be incorporated in the teaching of basic angle construction in plane geometry.