1. Introduction

HIV affects the immune system, making people infected with the virus at a higher risk of being infected by several other pathogens. It is important that those infected keep their bodies as healthy as possible by making sure that they get all the required nutrients. This will help to maintain and improve the performance of the immune system and hence increase the ability to fight against pathogens [1]. Poor nutrition worsens the effects of HIV by further failing the immune system, causing rapid progression of HIV to AIDS. It is known that food and nutritional intake can affect adherence to antiretroviral drugs (ARVs) as well as their effectiveness [2-3].

Recommended Dietary Intake (RDI) is the average daily dietary intake level that is sufficient to meet the nutrient requirements of nearly all (97–98 per cent) healthy individuals in a particular life stage and gender group [4]. Normally the RDI values are arranged according to age, weight, height and gender of individuals’ for normal persons [4-7].

People living with HIV (PLWHIV) have additional requirements of energy compared to non-infected persons. An adult with early infection (asymptomatic stage) needs 10% to 20% of extra energy while at symptomatic stage needs 20% to 30% extra energy above the recommended daily/dietary intake (RDI) compared to a non-infected adult of the same age and sex. Children with early infection (asymptomatic stage) require 10% extra energy, but 20% to 30% extra energy at symptomatic stage compared to a non-infected child of the same age and sex. There is no strong evidence to suggest that HIV infection increases protein, vitamins and mineral requirements above the RDI of the non-infected individuals [3, 8].

A linear programming model has been employed to model the diet for Malaysian boarding school caters with the aim of minimizing the budget provided by the Malaysian government and to maximize the variety of food intake [9]. Their model also wanted to achieve the maximum nutritional requirement based on the Malaysian Recommended Daily Allowance (RDA) requirements. Also, a linear programming optimization model has been used to model food consumption to meet daily nutrients needed by the standard woman and the standard man at the minimal cost respecting the World Health Organization (WHO) standards. The cost of foods to be minimized, is defined as the objective function in the optimization model [10]. Linear programming represents an influential tool for designing optimized diets, it is a useful mathematical method that can be used to easily translate accepted nutritional recommendations into sound food-based guidelines basing on locally available foods and local market prices. Besides, linear programming is much more efficient than the empirical “trial and error” approach currently used for formulating diets [11].

Elsewhere, linear programming model has been used to determine the balanced and least costly diets for different age groups who suffer from malnutrition due to deficiencies in their food budget in the poorest community in Greater Amman, Jordan [12].

Joseph C and colleagues [13] formulated a diet problem with a linear programming model. This formulation included the diet problem web page where the user is shown the steps to convert the verbal formulation of the problem into a mathematical problem. According to [14], a linear programming model is used to find a one-day ration food for a person to meet their nutritional requirements while minimizing cost.

Multiple linear regression analysis is carried out to prophesy the values of a dependent variable Y, given a set of N explanatory variables 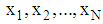[15]. Multiple regression analysis is a highly flexible system for observing the relationship of a collection of independent variables (or predictors) to a single dependent variable (or criterion). The independent variables may be quantitative or categorical [16].

Different researchers have described the importance of achieving nutrient recommendation for people living with HIV, but none (to our knowledge) has described how to achieve it using a simple model. Furthermore, different studies in diet modeling have not considered factors that determine nutrient required in the body during the optimization process. Without considering these factors over taking/under taking of the nutrients may result due to the fact that RDI values are determined by factors such as age, weight, height and gender of individuals. This paper aims to develop a mathematical model which combines multiple linear regression model and linear programming model. Multiple linear regression model will predict macro and micro nutrient required in the human body by an individual’s age, weight, height and gender, so as to avoid over or under taking nutrients, and linear programming model will compute adequate amount of foods that will determine optimal nutrients. The developed mathematical model will act as a tool to enable people living with HIV to achieve the nutrients recommended.

2. Research Methodology

In this paper, a linear programming and multiple linear regression models have been formulated and combined in order to form a cost effectiveness computing model that will be used to compute adequate amount of foods that will meet the optimal nutrients needs for people living with HIV at a minimized cost in consideration of age, weight, height and gender of an individual at an asymptomatic stage. The Recommended Dietary Intake (RDI) of nutrients used in this study is borrowed from [5-7] for normal persons. Energy requirements for PLWHIV have been obtained by adding 15% and 10% to a normal person’s requirement for adults and children respectively. The food composition table is suggested by [8].

3. Mathematical Model Formulation

The mathematical model is expected to predict the nutrient requirements in the human body and determine adequate amount of foods that will meet the optimal nutrients. The nutrient requirement will be predicted by the multiple linear regression model and the adequate amount of foods will be computed by the linear programming model.

3.1. Multiple Linear Regression Model

The regression analysis has assumptions to be met for its results to be considered valid, predictive and useful. In this paper, four main assumptions have been considered before starting the regression analysis. According to [17-19], it has been stated that the four assumptions which needs to be met include normality of errors (residuals), linearity of parameters in the model, assumptions about the model error, and assumption about measurement error (reliability).

3.1.1. Normality of Errors or Residuals

Errors are assumed to be normally distributed in any combination of values of the predictor variables, the properties of the errors are investigated by calculating the residuals of a regression model in the sample data. It should be noted that it is not necessary for predictors to be normally distributed [17-20].

3.1.2. Linearity of Parameters in the Model

The response variable is assumed to be a linear function of the parameters such as 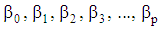but not necessarily a linear function of the predictor variables 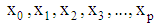[17-20].

3.1.3. Assumptions about the Model Error

According to [17, 19, 21-23], the assumptions about the model error include: mean of errors should be zero, independence of errors, homoscedasticity that is constant variation of errors and normal distribution of errors as has been named and explained above.

3.1.4. Assumption about Measurement Error (reliability)

It is assumed that predictor variables are measured without errors, and errors in the response variable are considered not harmful to inferences relating to unstandardized regression coefficients, provided this measurement error is not correlated with the predictor variable values [17-19].

Apart from the four assumptions above, the regression analysis put into consideration other factors such as a measure of goodness of fit , and the significance of the model and coefficients. We have performed a regression analysis of each nutrient as response variable on explanatory variables age (A), weight (W), height (H), and gender (G). Where A, W and H are continuous quantitative variables and G is a categorical variable. The regression analysis resulted in the following multiple linear regression model: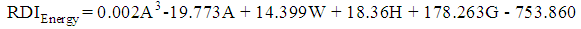

(1)

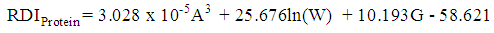(2)

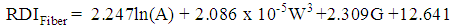(3)

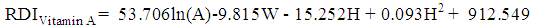(4)

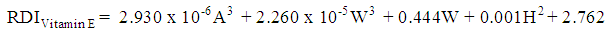(5)

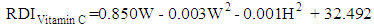(6)

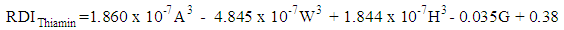(7)

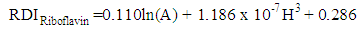(8)

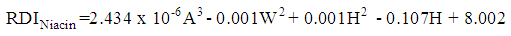(9)

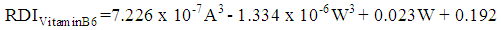(10)

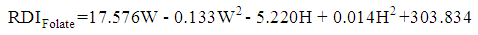(11)

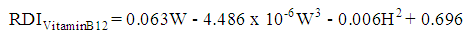(12)

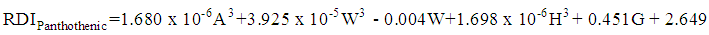(13)

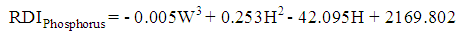(14)

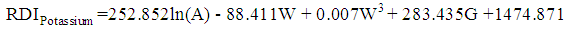(15)

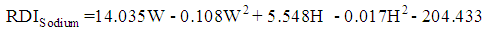(16)

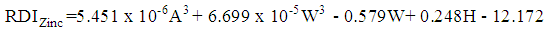(17)

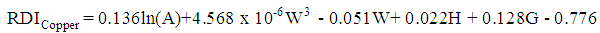(18)

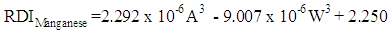(19)

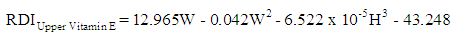(20)

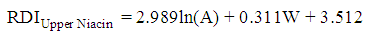(21)

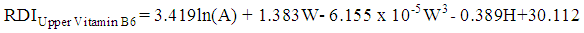(22)

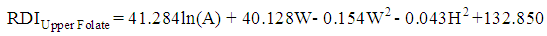(23)

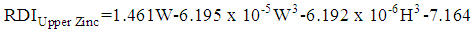(25)

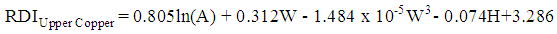(26)

3.2. Linear Programming Model

The linear programming model involves food items as variable 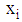, cost of food 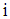as parameter 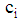, nutrient j contained in food 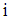is given as 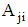. Moreover, 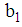is the maximum allowable amount of nutrient j, while 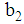is the minimum amount of nutrient j required and 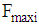is the maximum allowable amount of food , from the multiple linear regression model we define 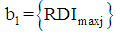and 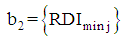where 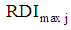is the set of multiple linear regression model for maximum recommended nutrient intake and 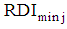is the set of multiple linear regression models for minimum recommended nutrient intake. Thus 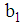include equations numbered 20 through 26, where 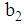include equations numbered 1 to 19. Mathematically, a linear programming model is written as:

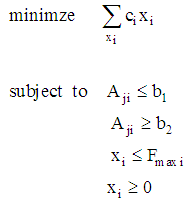(27)

4. Results

Results have been organized in two categories: the first is the predictive power of our multiple linear regression model and the second is the cost comparison incurred on buying the computed adequate amount of foods when the model predicted values are used and when RDI values are used as the nutritional recommendations.

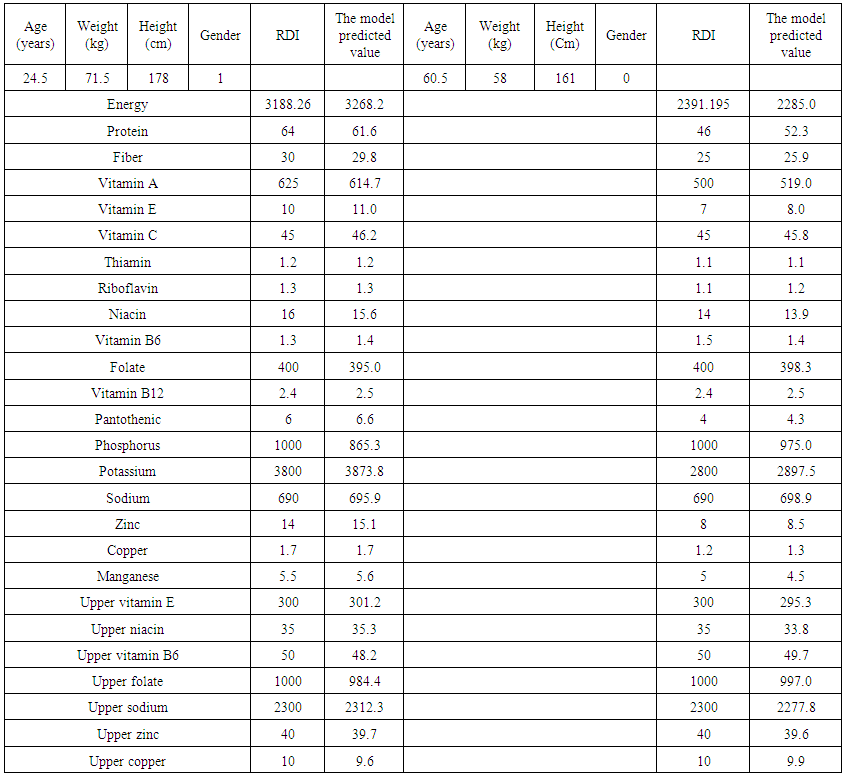Table 1. Comparison of model predicted values to the RDI value

4.1. Multiple Linear Regression Model Predictive Power

In this part we want to see the predictive power of the multiple linear regression model developed, we compare the values predicted by the model to the RDI values. The comparison is considering the model predicted values and RDI values for a specific individual. The gender has been arbitrary represented as 0 for women and 1 for men. We have randomly considered a man aged 24.5 years, weighing 71.5 kg, of height 178 cm and a woman of 60.5 years old, weighing 58 kg and of height 161 cm. The results were as in the Table 1 above.

From Table 1 above, the model predicted values are close enough to the RDI values, which shows that the model developed has high predictive power. This convinced us that the multiple linear regression model could be used to predict the nutritional recommendation to the human body by factors of age, weight, height and gender. The multiple linear regression model predicted values are categorize into the minimum amount of nutrients recommended and maximum amount of nutrients allowed. These results were used to limits/defines the constraints in the linear programming model, so as to find out adequate amount of foods that would meet the optimal nutrients required.

4.2. Linear Programming Model Result

A person who is infected with HIV/AIDS and is not showing signs of illness does not need a specific HIV-diet. However, those infected with HIV should make every effort to adopt healthy and balanced nutrition patterns in order to meet their increased energy requirements and maintain their nutritional status, so as to enable their immune systems fight against opportunistic diseases [24]. Suppose there are ten foods which are easily found in a certain area, these foods are rice with coconut milk, banana with meat and coconut milk, beef, avocado, papaya juice, spinach, African doughnut, cassava porridge, dried fresh water fish and green salad. From this list an individual can select what to eat. We have compared the cost incurred when we use the values of our multiple linear regression model and the actual RDI values. The formulated problem was solved by a two phase simplex method in MATLAB, we wrote the function TwoPhaseSimplex which calls the totbl and ljx functions in order to solve this problem by the two phase simplex method. The function totbl is used to display the tableau while the function ljx is used to exchange the pivot row and pivot column in the tableau [25-26]. The results from the problem were as follows:

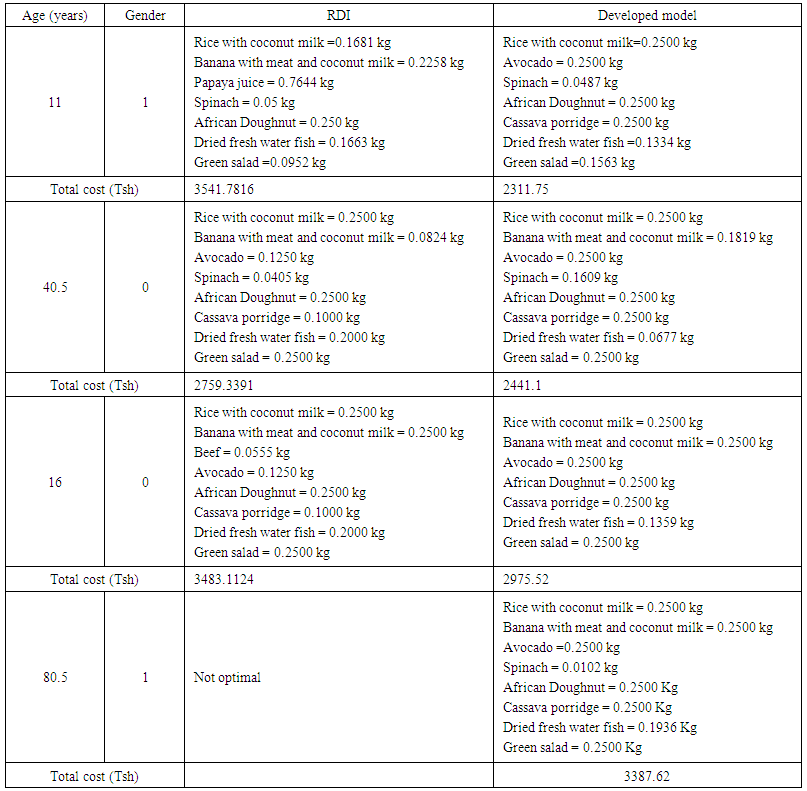Table 2. Cost comparison incurred for computing adequate amount of foods to reach the optimal nutrients using our model predicted values and using RDI values

The cost comparisons from Table 2 above can be presented graphically in Figure 1 below.

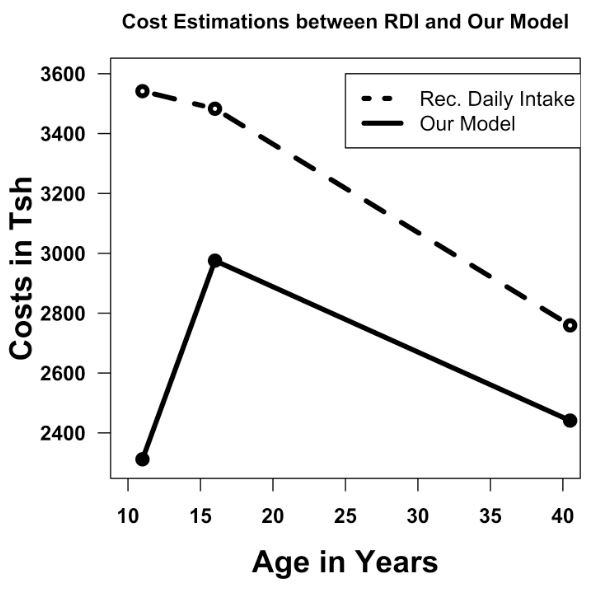Figure 1. Cost comparison when RDI values and model predicted values were used to compute adequate amount of foods to achieve recommended nutrients

Table 2 and Figure 1 shows that when multiple linear regression and linear programming models are combined they provide optimal nutrients for a cost much less than the RDI nutrient recommendations. For instance a young man who is 11 years old has met the optimal nutrients by the cost of TSH 3541.7816 when RDI values are used, but using our model he meets the optimal nutrients at TSH 2311.75, this cost has decreased by approximately 34.73%. A woman whose age is 40.5 years old is meeting her nutritional requirements at TSH 2759.3391 when RDI values are used, but uses only TSH 2441.1 to meet her nutritional recommendation using our model. The cost will decrease by approximately 11.53%. Similarly a woman aged 16 years old will use TSH 3483.1124 to meet the nutritional recommendation when RDI values are used while she will use TSH 2975.52 when the values of our model are used. The man whose age is 80.5 years will not meet the optimal nutrients from this food list if the RDI values are used, however, he will meet optimal nutrients using our model at a cost of TSH 3387.62. Thus, through this developed mathematical model, people living with HIV will be in a position to meet the amount of recommended nutrients at less cost.

5. Discussion and Conclusions

The paper has developed a mathematical model that can be used to manage the nutritional requirements for people living with HIV at an asymptomatic stage at least cost. This mathematical model combines multiple linear regression and linear programming models. Multiple linear regression models predict the nutritional requirements in the human body by factors of weight, age, height and gender and its results are the maximum allowable amount of nutrients and minimum amount of nutrients required. These results are used in the linear programming model to limit the constraints set. The linear programming model computes the adequate amount of foods that determine the optimal nutrients.

We saw that the multiple linear regression models have high predictive powers as their values were close enough to the actual values of RDI. The optimality in the linear programming is reached even when these two models are combined and good enough the optimal solution is at least cost-saving compared to RDI. This model has been considered because individuals of the same age and sex may not necessarily have the same weight and height, which make the difference of nutrient required in the body. By providing optimal estimates, our model avoids over or undertakings of the nutrients for the patient thus ensuring a balanced nutrient intake for them. The model predicts optimal nutritional recommendation at a cost lower than that predicted from RDI, which will enable more people to have a balanced diet. In the absence of HIV/AIDS cure this will help individuals to live healthier and continue having a positive contribution at the household and national levels both socially and economically. The model developed can be extended to different groups of people who must manage their diets and therefore promises to have a wider applicability.

The study is limited to a few nutrients as we have considered nineteenth nutrients, this was done for demonstration purposes. The fact that our model has shown to produce useful information makes us eager to extend it by adding even more nutrients in the future. Another future plan is development of a graphical user interface (GUI) in different programming languages, web page or mobile application that will give opportunity to clients just to select the foods they want to eat, submit their age, weight, height and gender, but also the cost of foods they have chosen and obtain the adequate amount of foods that will meet their optimal nutrient requirements at a minimized cost.