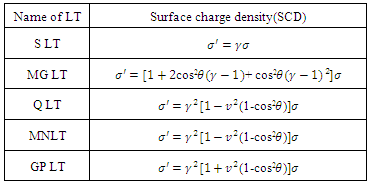S. A. Bhuiyan, A. R. Baizid
Department of Business Administration, Leading University, Sylhet, Bangladesh
Correspondence to: S. A. Bhuiyan, Department of Business Administration, Leading University, Sylhet, Bangladesh.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Lorentz transformation is a group transformation that is used to transform the space and time coordinates of one inertial frame of reference into another one with travelling at a relative speed. Lorentz transformation is the basic tool for the study of Relativistic Mechanics. There are different types of Lorentz transformations such as Special, Most general, Mixed number, Geometric product and Quaternion Lorentz transformations. In this paper we have studied the surface charge density in different types of Lorentz Transformations.
Keywords:
Lorentz Transformation (LT), Most General Lorentz Transformation (MGLT), Mixed Number Lorentz Transformation (MNLT), Geometric Product Lorentz Transformation (GPLT), Quaternion Lorentz Transformation (QLT), Surface Charge Density (SCD)
Cite this paper: S. A. Bhuiyan, A. R. Baizid, Surface Charge Density in Different Types of Lorentz Transformations, Applied Mathematics, Vol. 5 No. 3, 2015, pp. 57-67. doi: 10.5923/j.am.20150503.01.
1. Introduction
In most treatments on special relativity [1], the line of motion is aligned with x-axis. In such a situation the (y-z) coordinates are invariant under the LT. However, it is of interest to study the case when the line of motion does not coincide with any of the coordinate axes. In this paper we have derived the formula for SCD in different types of LTs when the line of motion is not aligned with any of the coordinate axes.
1.1. Special Lorentz Transformation
Let us consider two inertial frames of references S and S', where the frame S is at rest and the frame S' moving along the X axis with the velocity 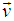 with respect to the S frame. The space and time coordinates of S and S' are
with respect to the S frame. The space and time coordinates of S and S' are  and
and  respectively. The relation between then coordinates of S and S', which is called the special Lorentz transformation, can be written as [1]
respectively. The relation between then coordinates of S and S', which is called the special Lorentz transformation, can be written as [1]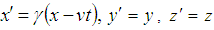 | (1) |
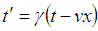 , where
, where 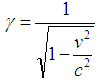 and c = 1And
and c = 1And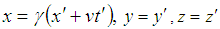 | (2) |


1.2. Most General Lorentz Transformation
When the velocity 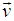 of S' with respect to S is not along the X axis, i.e. the velocity
of S' with respect to S is not along the X axis, i.e. the velocity 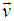 has three components vx, vy and vz then the relation between the coordinates of S and S', which is called the MGLT, can be written as [1]
has three components vx, vy and vz then the relation between the coordinates of S and S', which is called the MGLT, can be written as [1] 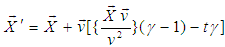 | (3) |
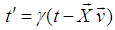 , where
, where 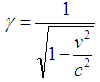 and c = 1The inverse MGLT can be written as [1]
and c = 1The inverse MGLT can be written as [1]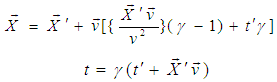 | (4) |
1.3. Mixed Number Lorentz Transformation
MNLT can be generated using Mixed number algebra. [1, 5-9]. Let us consider the velocity 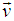 of S' with respect to S is not along the X axis, i.e. the velocity
of S' with respect to S is not along the X axis, i.e. the velocity 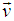 has three components vx,vy and vz. Let in this case
has three components vx,vy and vz. Let in this case 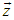 and
and 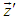 can be the space part in S and S' frame respectively. Then the MNLT can be written as [1, 3, 5-9]
can be the space part in S and S' frame respectively. Then the MNLT can be written as [1, 3, 5-9] 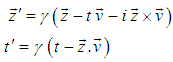 | (5) |
The inverse MNLT can be written as [1]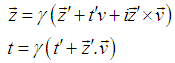 | (6) |
1.4. Geometric Product Lorentz Transformation
Bidyut Kumar Datta and his co-workers defined the geometric product of vectors as [2, 14, 15] 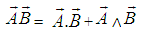 Where
Where 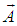 and
and 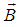 are two vectors.
are two vectors. 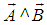 . i.e A wedge B, it has magnitude
. i.e A wedge B, it has magnitude 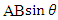 and it is different from the usual cross product. It is not a scalar or vector. Geometric product of two perpendicular vectors is an area or a bivector oriented in the plane containing the vectors and Geometric product of two parallel vectors is simply the scalar product of the vectors [16]. We use the symbol
and it is different from the usual cross product. It is not a scalar or vector. Geometric product of two perpendicular vectors is an area or a bivector oriented in the plane containing the vectors and Geometric product of two parallel vectors is simply the scalar product of the vectors [16]. We use the symbol  instead of the symbol
instead of the symbol 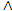 .. Therefore the geometric product of vectors can be written as [2]
.. Therefore the geometric product of vectors can be written as [2] 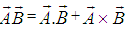 | (7) |
We can also generate a type of most general Lorentz transformation using this geometric product.In this case the velocity 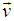 of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case
of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case 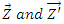 be the space parts in the S and S' frames respectively. Then the GPLT can be written as [2]
be the space parts in the S and S' frames respectively. Then the GPLT can be written as [2]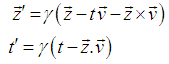 | (8) |
The inverse GPLT can be written as [2]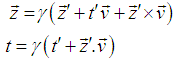 | (9) |
1.5. Quaternion Lorentz Transformation
The Quaternion can also be written as the sum of a scalar and a vector [2] i.e, 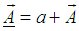 . The multiplication of any two quaternion’s
. The multiplication of any two quaternion’s 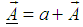 and
and 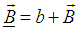 is given by [2]
is given by [2] 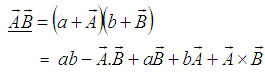 | (10) |
Taking a= b = 0, we get 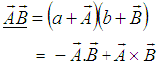 | (11) |
This product is called quaternion product. We can also generate a type of most general Lorentz transformation using this quaternion product.In this case the velocity 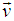 of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case
of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case 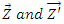 be the space parts in the S and S' frames respectively. Then the QLT can be written as [2]
be the space parts in the S and S' frames respectively. Then the QLT can be written as [2] 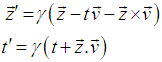 | (12) |
The inverse QLT can be written as [2]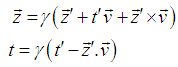 | (13) |
2. Surface Charge Density
The charge density is the amount of electric charge (the number of electrons, ions) per unit volume of space in one, two or three dimensions. The surface charge density 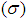 is the amount of electric charge per unit surface area (A).
is the amount of electric charge per unit surface area (A). 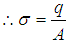 It is measured in coulombs per square meter(C/m2) [1]. Since there are positive as well as negative charges, the charge density can take on negative values. Like any density it can depend on position. We know that the charge on the electron or proton is the minimum, called the elementary charge e (= 1.6×10-19coul). The electric charge is discrete which may be determined by counting the number of elementary charged particles. As the total number of elementary charges cannot depend on the state of the motion of the observer, we may conclude that the electric charge is relativistically invariant. Based on this information we want to discuss the surface charge density
It is measured in coulombs per square meter(C/m2) [1]. Since there are positive as well as negative charges, the charge density can take on negative values. Like any density it can depend on position. We know that the charge on the electron or proton is the minimum, called the elementary charge e (= 1.6×10-19coul). The electric charge is discrete which may be determined by counting the number of elementary charged particles. As the total number of elementary charges cannot depend on the state of the motion of the observer, we may conclude that the electric charge is relativistically invariant. Based on this information we want to discuss the surface charge density 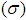 in different types of Lorentz transformation.
in different types of Lorentz transformation.
3. Surface Charge Density in Different Types of Lorentz Transformation
3.1. Surface Charge Density in Special Lorentz Transformation
Let us consider two system S and S', S' is moving with uniform velocity 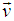 relative to S along negative direction of X-axis as shown in Figure 1. Let there be a stationary sheet of uniform charge density
relative to S along negative direction of X-axis as shown in Figure 1. Let there be a stationary sheet of uniform charge density 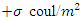 at rest in system S having one edge parallel to X'-axis. Let the sheet be a square of side L0 and placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving with velocity
at rest in system S having one edge parallel to X'-axis. Let the sheet be a square of side L0 and placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving with velocity 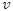 along (+) ve X-axis.We have the transformation formula for the surface charge density in Special Lorentz transformation which is given [1] as
along (+) ve X-axis.We have the transformation formula for the surface charge density in Special Lorentz transformation which is given [1] as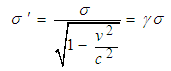 | (14) |
Where 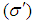 is the surface charge density of the moving frame.
is the surface charge density of the moving frame.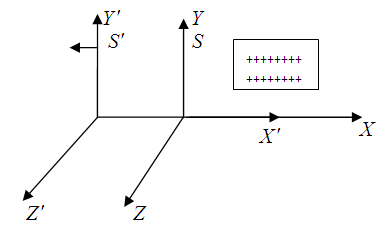 | Figure 1. The system S' is moving along X-axis with velocity 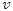 relative to the system S relative to the system S |
3.2. Surface Charge Density in Most general Lorentz Transformation
Let us consider two system S and S' where the frame S' is moving with velocity 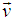 relative to the system S along X-Y plane as shown in Figure 2. Thus the velocity of
relative to the system S along X-Y plane as shown in Figure 2. Thus the velocity of 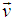 has two components
has two components 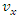 and
and 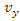 . Let us consider a stationary sheet of uniform charge density
. Let us consider a stationary sheet of uniform charge density 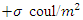 at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction.Therefore the surface charge density in MGLT is discussed in [1] and the transformation equation of surface charge density in MGLT is derived as
at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction.Therefore the surface charge density in MGLT is discussed in [1] and the transformation equation of surface charge density in MGLT is derived as 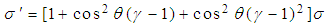 | (15) |
Where 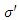 represent the surface charge density when the system S' is moving along X-Y plane.
represent the surface charge density when the system S' is moving along X-Y plane.
3.3. Surface Charge Density in Mixed Number Lorentz Transformation
Again according to the systems described in 3.2 we have the transformation formula for the surface charge density in MNLT which is derived in [1] can be written as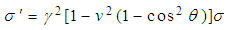 | (16) |
3.4. Surface Charge Density in Geometric product Lorentz Transformation
Let us consider two system S and S' where the frame S' is moving with velocity 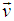 relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of
relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of 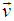 has two components
has two components 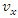 and
and 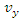 .
.  | Figure 2. The system S' is moving in X-Y plane with velocity 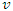 relative to the system S relative to the system S |
Let us consider a stationary sheet of uniform charge density 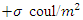 at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity
at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity  along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the GPLT can be written as [4]
along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the GPLT can be written as [4] 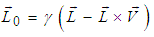
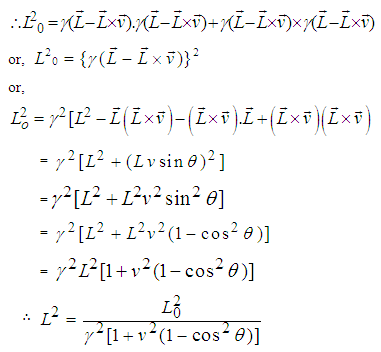 Considering L has two components
Considering L has two components 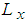 and
and 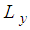 .
.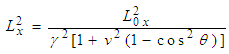 and
and 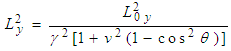 The total charge observed by an observer in S' is
The total charge observed by an observer in S' is 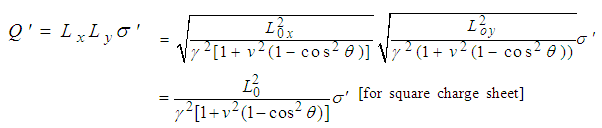 | (17) |
Where 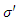 is the surface charge density in system S'. According to the principle of conservation of charge
is the surface charge density in system S'. According to the principle of conservation of charge 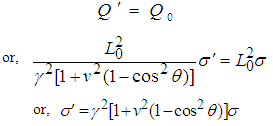 | (18) |
This equation represents the transformation equation for surface charge density in GPLT.
3.5. Surface Charge Density in Quaternion Lorentz Transformation
Let us consider two system S and S' where the frame S' is moving with velocity 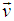 relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of
relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of 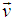 has two components
has two components 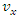 and
and 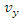 . Let us consider a stationary sheet of uniform charge density
. Let us consider a stationary sheet of uniform charge density 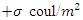 at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity
at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity 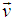 along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the QLT can be written as [4]
along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the QLT can be written as [4] 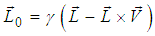
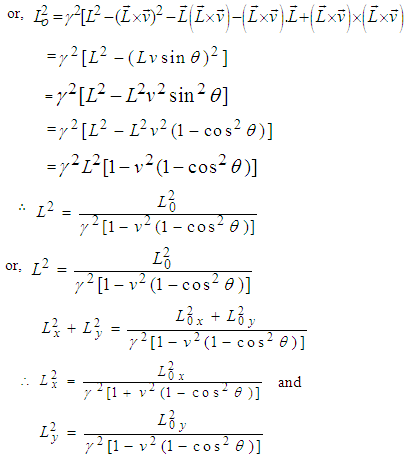 The total charge observed by an observer in S' is
The total charge observed by an observer in S' is 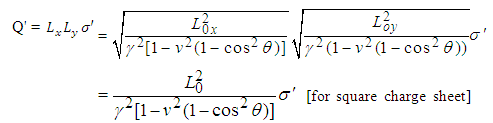 | (19) |
Where 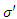 is the surface charge density in system S'. According to the principle of conservation of charge
is the surface charge density in system S'. According to the principle of conservation of charge 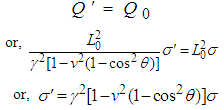 | (20) |
This equation represents the transformation equation for surface charge density in QLT.
4. Comparative Study
4.1. Table 1
Table 1. Surface charge density in different types of Lorentz transformations (LT)
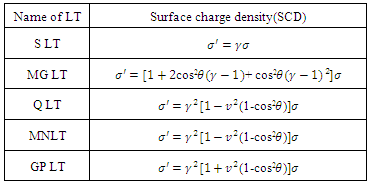 |
| |
|
4.2. Graphical Representation of SCD in Different Types of LTs
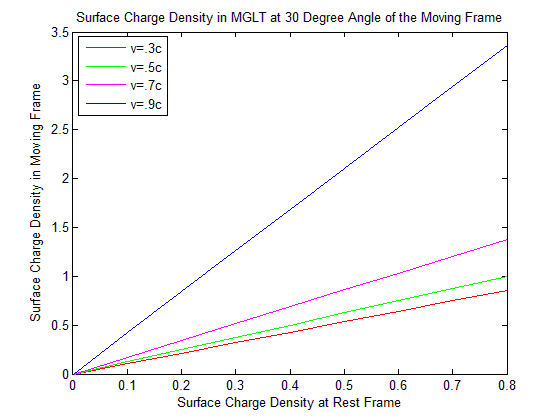 | Figure 3. Surface Charge Density in MGLT at 30 Degree Angle of the moving Frame |
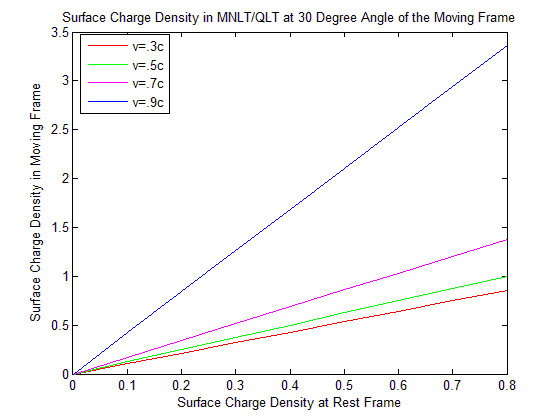 | Figure 4. Surface Charge Density in MNLT/QLT at 30 Degree Angle of the Moving Frame |
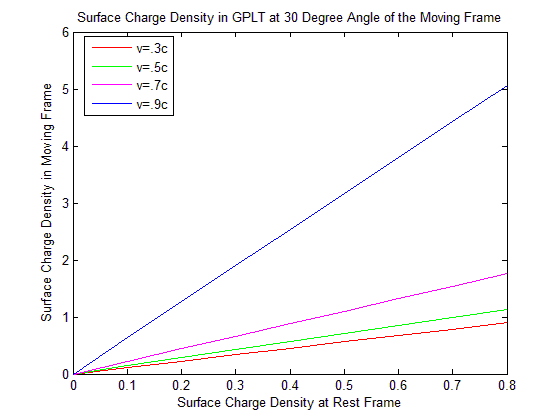 | Figure 5. Surface Charge Density in GPLT at 30 Degree Angle of the Moving Frame |
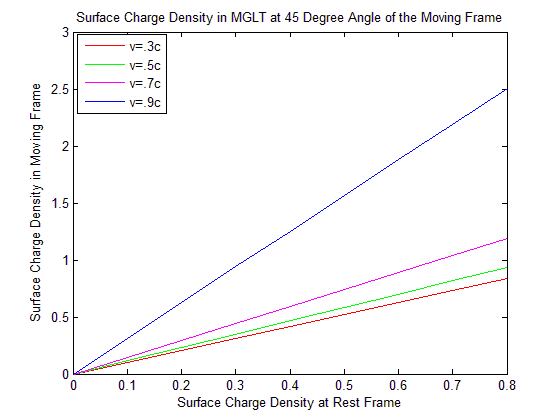 | Figure 6. Surface Charge Density in MGLT at 45 Degree Angle of the Moving Frame |
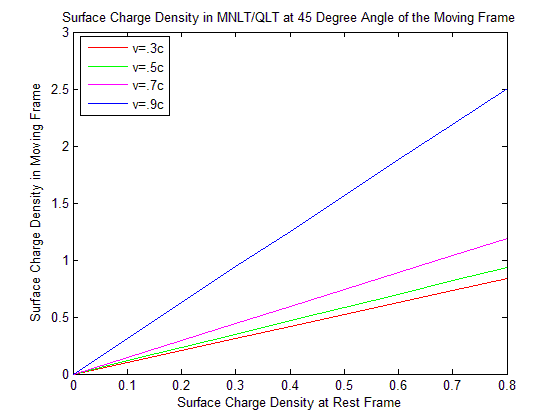 | Figure 7. Surface Charge Density in MNLT/QLT at 45 Degree Angle of the Moving Frame |
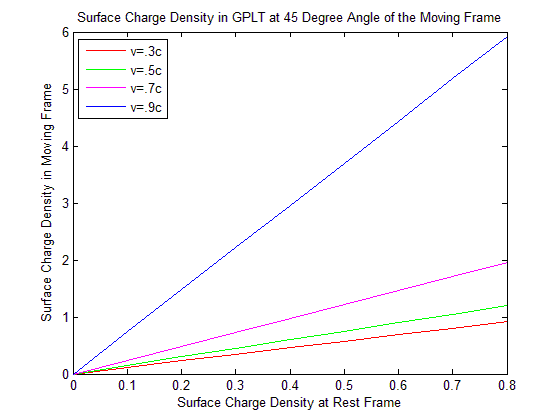 | Figure 8. Surface Charge Density in GPLT at 30 Degree Angle of the Moving Frame |
 | Figure 9. Surface Charge Density in MNLT/QLT at 30 Degree Angle of the Moving Frame |
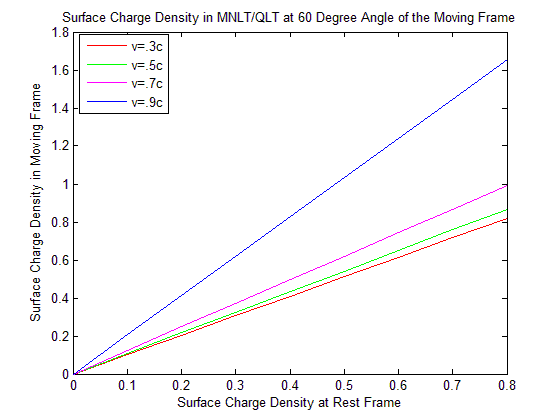 | Figure 10. Surface Charge Density in MNLT/QLT at 30 Degree Angle of the Moving Frame |
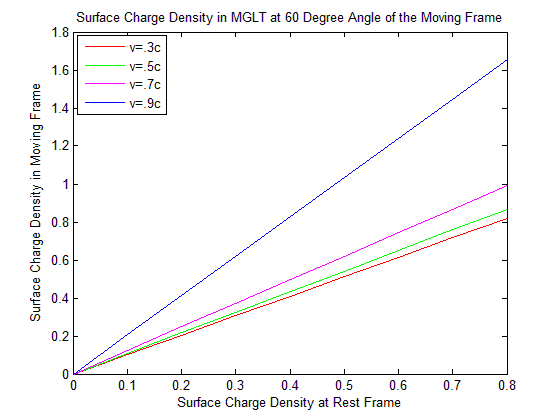
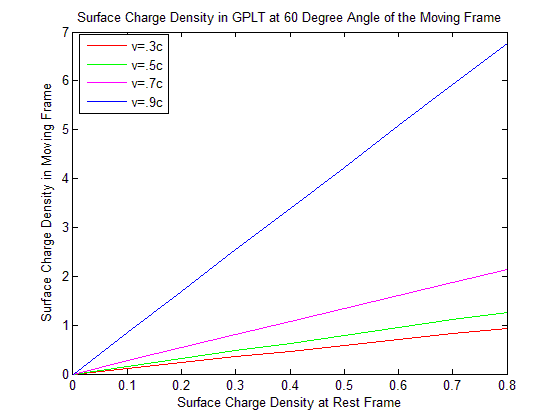 | Figure 11. Surface Charge Density in GPLT at 60 Degree Angle of the Moving Frame |
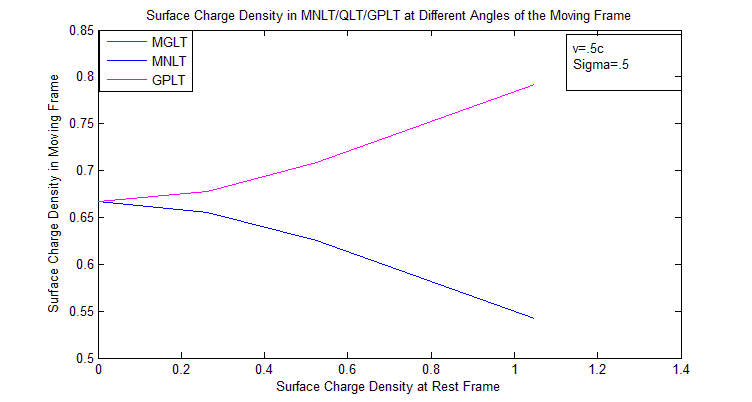 | Figure 12. Surface Charge Density in MGLT/MNLT/GPLT at Different Angles of the Moving Frame |
Discussion: For the less velocity of the moving frame there exist slightly changes of the surface charge density. But when the velocity of the moving frame is very close to the speed of light the change of surface charge density is highly remarkable.Discussions: We see from the Figure 12 surface charge density is increasing in GPLT at fixed velocity and fixed surface charge density at rest frame when angle is increasing. But in MNLT it is decreasing. The surface charge density in MGLT of the moving frame is same as in MNLT. So it is coincide with MNLT and not visible in the graph.
5. Conclusions
The transformation formulae for surface charge density in SLT, MGLT, QLT, MNLT and GPLT are illustrated in Table 1. The numerical values of surface charge densities of the moving system in terms of a system at rest for different types of LTs have calculated and it has observed graphically that for same angle 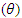 between system S and S', the values of surface charge density of moving system,
between system S and S', the values of surface charge density of moving system, 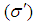 increases with increasing velocity
increases with increasing velocity 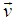 of the moving system and for the same velocity of the moving system
of the moving system and for the same velocity of the moving system 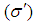 decreases with increasing angle
decreases with increasing angle 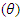 but in GPLT for the same velocity of the moving system
but in GPLT for the same velocity of the moving system 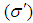 increases with increasing angle
increases with increasing angle 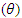 .
.
References
| [1] | S.B Rafiq and M.S Alam , Transformation of Surface Charge Density in Mixed Number Lorentz Transformation, Sri Lankan Journal of Physics, Vol.13(1)(2012) 17-25. |
| [2] | Atikur Rahman Baizid & Md. Shah Alam, Reciprocal Property of Different Types of Lorentz Transformation, International Journal of Reciprocal Symmetry and Theoretical Physics,volume1, No 1(2014). |
| [3] | M.S. Alam, S. Bauk and M. Ahmed, Agreements and disagreements between Lorentz transformation and von Peschke’s comment, Physics Essays 24, (2011)1. |
| [4] | M.S. Alam, K. Begum, Different types of Lorentz transformation, Jahangirnagar Physics Studies. 15, (2009). |
| [5] | M. S. Alam, Mixed Product of vectors, Journal of Theoretics. 3, (2001) 4. |
| [6] | M.S. Alam, M.H. Ahsan and M. Ahmad, Mathematical Tools of Mixed-Number algebra J. Natn. Sci. Foundation, Sri Lanka. 33, (2005)1. |
| [7] | M.S. Alam, M.H. Ahsan, Mixed-Number Lorentz Transformation, Physics Essays, 16, (2003) 4. |
| [8] | M.S. Alam, Consequences of Mixed Number Lorentz Transformation, Proc. Pakistan Acad. Sci. 41, (2004) 2. |
| [9] | M. S. Alam, M.D. Chowdhury, Relativistic aberration of Mixed number Lorentz transformation, J. Natn. Sci. Foundation Sri Lanka. 34, (2005) 3. |
| [10] | M.S. Alam, Comparative Study of Mixed Product and Quaternion Product, Indian Journal of Physics A 77, (2003). |
| [11] | M.S. Alam, Comparative Study of Quaternions and Mixed Number, Journal of Theoretics. 3, (2001) 6. |
| [12] | Md. Shah Alam and Sabar Bauk, Comparative Study of Geometric product and Mixed product. Proceedings of the 6th IMT-GT conference on Mathematics, Statistics and its Applications (ICMSA2010) Universiti Tunku Abdul Rahman, Kuala Lumpur, Malaysia. |
| [13] | M. R. Spiegel, Theory and Problems of Vector Analysis and An Introduction to Tensor Analysis, Schaum’s outline series, McGraw-Hill book company. |
| [14] | Datta, B.K, De Sabbata V. and Ronchetti L. 1998. Quantization of gravity in real space time, II Nuovo Cimento, 113 B. |
| [15] | Datta, B.K., Datt a R. 1998. Einstein field equations in spinor formalism, Foundations of Physics letters, 11,1. |

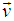 with respect to the S frame. The space and time coordinates of S and S' are
with respect to the S frame. The space and time coordinates of S and S' are 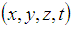 and
and 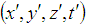 respectively. The relation between then coordinates of S and S', which is called the special Lorentz transformation, can be written as [1]
respectively. The relation between then coordinates of S and S', which is called the special Lorentz transformation, can be written as [1]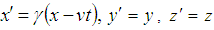
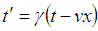 , where
, where 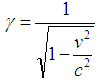 and c = 1And
and c = 1And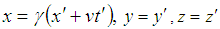


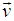 of S' with respect to S is not along the X axis, i.e. the velocity
of S' with respect to S is not along the X axis, i.e. the velocity 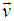 has three components vx, vy and vz then the relation between the coordinates of S and S', which is called the MGLT, can be written as [1]
has three components vx, vy and vz then the relation between the coordinates of S and S', which is called the MGLT, can be written as [1] 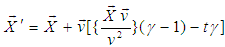
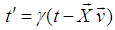 , where
, where 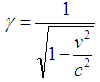 and c = 1The inverse MGLT can be written as [1]
and c = 1The inverse MGLT can be written as [1]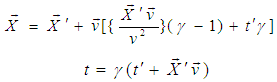
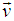 of S' with respect to S is not along the X axis, i.e. the velocity
of S' with respect to S is not along the X axis, i.e. the velocity 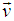 has three components vx,vy and vz. Let in this case
has three components vx,vy and vz. Let in this case 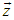 and
and 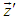 can be the space part in S and S' frame respectively. Then the MNLT can be written as [1, 3, 5-9]
can be the space part in S and S' frame respectively. Then the MNLT can be written as [1, 3, 5-9] 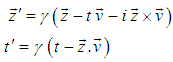
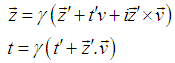
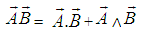 Where
Where 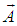 and
and 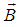 are two vectors.
are two vectors. 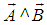 . i.e A wedge B, it has magnitude
. i.e A wedge B, it has magnitude 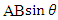 and it is different from the usual cross product. It is not a scalar or vector. Geometric product of two perpendicular vectors is an area or a bivector oriented in the plane containing the vectors and Geometric product of two parallel vectors is simply the scalar product of the vectors [16]. We use the symbol
and it is different from the usual cross product. It is not a scalar or vector. Geometric product of two perpendicular vectors is an area or a bivector oriented in the plane containing the vectors and Geometric product of two parallel vectors is simply the scalar product of the vectors [16]. We use the symbol  instead of the symbol
instead of the symbol 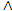 .. Therefore the geometric product of vectors can be written as [2]
.. Therefore the geometric product of vectors can be written as [2] 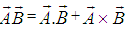
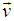 of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case
of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case 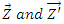 be the space parts in the S and S' frames respectively. Then the GPLT can be written as [2]
be the space parts in the S and S' frames respectively. Then the GPLT can be written as [2]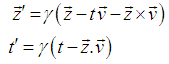
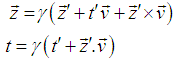
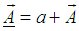 . The multiplication of any two quaternion’s
. The multiplication of any two quaternion’s 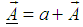 and
and 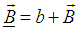 is given by [2]
is given by [2] 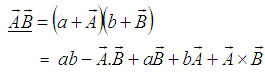
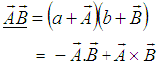
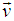 of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case
of S' with respect to S also has three components vx, vy and vz as the MGLT. Let in this case 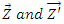 be the space parts in the S and S' frames respectively. Then the QLT can be written as [2]
be the space parts in the S and S' frames respectively. Then the QLT can be written as [2] 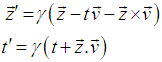
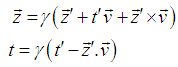
 is the amount of electric charge per unit surface area (A).
is the amount of electric charge per unit surface area (A). 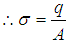 It is measured in coulombs per square meter(C/m2) [1]. Since there are positive as well as negative charges, the charge density can take on negative values. Like any density it can depend on position. We know that the charge on the electron or proton is the minimum, called the elementary charge e (= 1.6×10-19coul). The electric charge is discrete which may be determined by counting the number of elementary charged particles. As the total number of elementary charges cannot depend on the state of the motion of the observer, we may conclude that the electric charge is relativistically invariant. Based on this information we want to discuss the surface charge density
It is measured in coulombs per square meter(C/m2) [1]. Since there are positive as well as negative charges, the charge density can take on negative values. Like any density it can depend on position. We know that the charge on the electron or proton is the minimum, called the elementary charge e (= 1.6×10-19coul). The electric charge is discrete which may be determined by counting the number of elementary charged particles. As the total number of elementary charges cannot depend on the state of the motion of the observer, we may conclude that the electric charge is relativistically invariant. Based on this information we want to discuss the surface charge density  in different types of Lorentz transformation.
in different types of Lorentz transformation. relative to S along negative direction of X-axis as shown in Figure 1. Let there be a stationary sheet of uniform charge density
relative to S along negative direction of X-axis as shown in Figure 1. Let there be a stationary sheet of uniform charge density  at rest in system S having one edge parallel to X'-axis. Let the sheet be a square of side L0 and placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving with velocity
at rest in system S having one edge parallel to X'-axis. Let the sheet be a square of side L0 and placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving with velocity 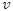 along (+) ve X-axis.We have the transformation formula for the surface charge density in Special Lorentz transformation which is given [1] as
along (+) ve X-axis.We have the transformation formula for the surface charge density in Special Lorentz transformation which is given [1] as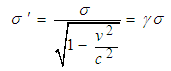
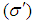 is the surface charge density of the moving frame.
is the surface charge density of the moving frame.
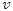 relative to the system S
relative to the system S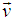 relative to the system S along X-Y plane as shown in Figure 2. Thus the velocity of
relative to the system S along X-Y plane as shown in Figure 2. Thus the velocity of 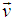 has two components
has two components 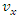 and
and 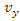 . Let us consider a stationary sheet of uniform charge density
. Let us consider a stationary sheet of uniform charge density 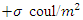 at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction.Therefore the surface charge density in MGLT is discussed in [1] and the transformation equation of surface charge density in MGLT is derived as
at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction.Therefore the surface charge density in MGLT is discussed in [1] and the transformation equation of surface charge density in MGLT is derived as 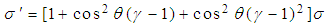
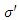 represent the surface charge density when the system S' is moving along X-Y plane.
represent the surface charge density when the system S' is moving along X-Y plane.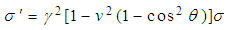
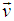 relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of
relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of 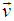 has two components
has two components 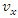 and
and 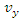 .
. 
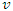 relative to the system S
relative to the system S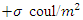 at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity
at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity 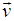 along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the GPLT can be written as [4]
along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the GPLT can be written as [4] 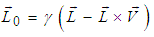
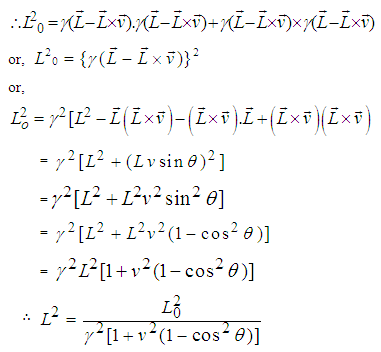 Considering L has two components
Considering L has two components 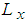 and
and 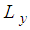 .
.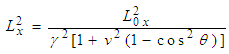 and
and 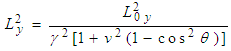 The total charge observed by an observer in S' is
The total charge observed by an observer in S' is 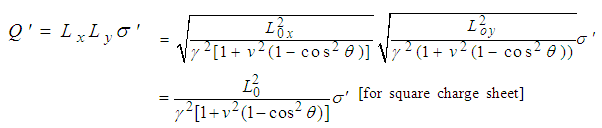
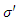 is the surface charge density in system S'. According to the principle of conservation of charge
is the surface charge density in system S'. According to the principle of conservation of charge 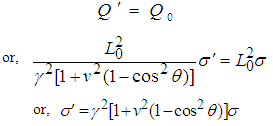
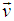 relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of
relative to the system S along any arbitrary direction as shown in the Figure 2. Thus the velocity of 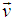 has two components
has two components 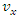 and
and 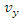 . Let us consider a stationary sheet of uniform charge density
. Let us consider a stationary sheet of uniform charge density 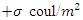 at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity
at rest in system S having one edge parallel to X-axis and let the sheet be a square of side L0 placed parallel to X-Y plane. The observer in the system S' will observe that the sheet is moving in opposite direction with velocity 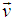 along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the QLT can be written as [4]
along any arbitrary direction as shown in Figure 2.If L0 is the length of the square charged sheet in S, then the length contraction in the moving frame for the QLT can be written as [4] 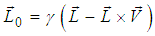
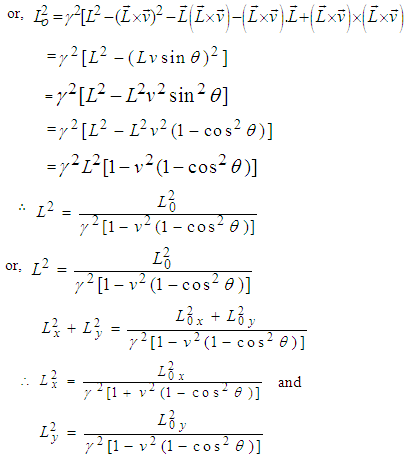 The total charge observed by an observer in S' is
The total charge observed by an observer in S' is 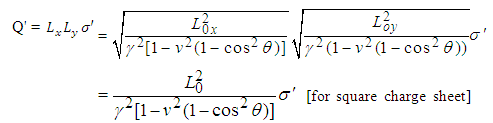
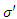 is the surface charge density in system S'. According to the principle of conservation of charge
is the surface charge density in system S'. According to the principle of conservation of charge 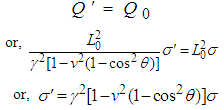










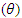 between system S and S', the values of surface charge density of moving system,
between system S and S', the values of surface charge density of moving system, 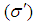 increases with increasing velocity
increases with increasing velocity 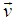 of the moving system and for the same velocity of the moving system
of the moving system and for the same velocity of the moving system 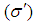 decreases with increasing angle
decreases with increasing angle 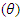 but in GPLT for the same velocity of the moving system
but in GPLT for the same velocity of the moving system 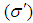 increases with increasing angle
increases with increasing angle 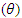 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML