-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2015; 5(1): 21-32
doi:10.5923/j.am.20150501.04
Non-Linear Reaction Diffusion Equation with Michaelis-Menten Kinetics and Adomian Decomposition Method
M. Renuga Devi 1, S. Sevukaperumal 2, L. Rajendran 3
1Department of Mathematics, P. M. T. College, Usilampatti, Madurai, Tamilnadu
2Ganesar College of Arts and Science, Melaisivapuri, Tamilnadu
3Department of Mathematics, The Madura College, Madurai, Tamilnadu
Correspondence to: L. Rajendran , Department of Mathematics, The Madura College, Madurai, Tamilnadu.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The mathematical model of reaction diffusion problem with Michaelis-Menten kinetics in a solid of planar and spherical shape is discussed. A simple series solution for the substrate concentration is obtained as a function of the Thiele modulus, modified Sherwood number, and the Michaelis constant. Here the Adomian decomposition method (ADM) is used to find the analytical expressions for the concentration of substrate and effectiveness factor. The numerical simulation of non-linear equations was carried out using the Matlab program. A comparison of the analytical approximation and numerical simulation is also presented. A good agreement between analytical and numerical results is observed.
Keywords: Mathematical Modeling, Non-Linear Diffusion-Reaction Equation, Michaelis-Menten Kinetics, The Adomian Decomposition Method
Cite this paper: M. Renuga Devi , S. Sevukaperumal , L. Rajendran , Non-Linear Reaction Diffusion Equation with Michaelis-Menten Kinetics and Adomian Decomposition Method, Applied Mathematics, Vol. 5 No. 1, 2015, pp. 21-32. doi: 10.5923/j.am.20150501.04.
Article Outline
1. Introduction
- The modern theory of the nonlinear processing is an important field of today science. The nonlinear system and coherent structures represent an interdisciplinary area with many nonlinear applications in physics (nonlinear optics, nonlinear electric circuits, hydrodynamics, plasmas and states of solid), general relativity, chemistry (chemical reactions), biology (atmosphere and oceans, animal dispersal), random media and modern telecommunications. A great variety of phenomena in physics, chemistry or biology can be described by nonlinear PDEs and particularly by reaction-diffusion equations. For these reasons, the theory of the analytical solutions of the reaction-diffusion equations is considered. The general form of nonlinear parabolic reaction diffusion equation
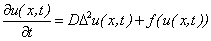 | (1) |
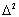 denotes the Laplace operator. So the first term on the right hand side describes the diffusion, including D as diffusion coefficient. The second term,
denotes the Laplace operator. So the first term on the right hand side describes the diffusion, including D as diffusion coefficient. The second term, 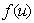 is a smooth function
is a smooth function 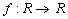 and describes the processes with really “change” the present
and describes the processes with really “change” the present 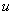 , i.e. something happens to it (birth, death, chemical reaction), not just diffuse in the space. It is also possible, that the reaction term depends not only
, i.e. something happens to it (birth, death, chemical reaction), not just diffuse in the space. It is also possible, that the reaction term depends not only 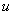 but also on the first derivative of
but also on the first derivative of 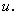 It appears in population dynamics, combustion theory and chemical kinetics. Reaction-diffusion equations are closely connected to the large deviation problems for diffusion processes.Many problems in theoretical and experimental biology involve the solution of the steady-state reaction diffusion equation with nonlinear chemical kinetics. Such problems arise in the formulation of substrate and product material balances for enzymes immobilized within particles [1, 2], in the description of substrate transport into microbial cells [3-5], in membrane transport, in the transfer of oxygen to respiring tissue [6, 7] and in the analysis of any artificial kidney system [8]. For such cases, the problem is often well poised as a two-point nonlinear boundary –value problem because of the saturation, Michaelis-Menten, or Monod expression used to describe consumption of the substrate. The Michaelis-Menten kinetics [9] is the one of the simplest and best-known model for the non-linear reaction diffusion process. It takes the form of an equation relating reaction velocity to substrate concentration for a system where the substrate
It appears in population dynamics, combustion theory and chemical kinetics. Reaction-diffusion equations are closely connected to the large deviation problems for diffusion processes.Many problems in theoretical and experimental biology involve the solution of the steady-state reaction diffusion equation with nonlinear chemical kinetics. Such problems arise in the formulation of substrate and product material balances for enzymes immobilized within particles [1, 2], in the description of substrate transport into microbial cells [3-5], in membrane transport, in the transfer of oxygen to respiring tissue [6, 7] and in the analysis of any artificial kidney system [8]. For such cases, the problem is often well poised as a two-point nonlinear boundary –value problem because of the saturation, Michaelis-Menten, or Monod expression used to describe consumption of the substrate. The Michaelis-Menten kinetics [9] is the one of the simplest and best-known model for the non-linear reaction diffusion process. It takes the form of an equation relating reaction velocity to substrate concentration for a system where the substrate 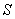 binds reversibly to an enzyme
binds reversibly to an enzyme 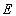 to form an enzyme-substrate complex
to form an enzyme-substrate complex 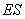 , which then reacts irreversibly to generate a product P and regenerate to free enzyme
, which then reacts irreversibly to generate a product P and regenerate to free enzyme 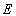 . This system can be represented schematically as follows:
. This system can be represented schematically as follows: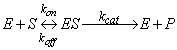 | (2) |
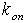 is the bimolecular association rate constant of enzyme-substrate binding;
is the bimolecular association rate constant of enzyme-substrate binding; 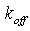 is the unimolecular rate constant of the
is the unimolecular rate constant of the 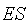 complex dissociating to regenerate free enzyme and substrate; and
complex dissociating to regenerate free enzyme and substrate; and 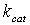 is the unimolecular rate constant of the
is the unimolecular rate constant of the 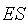 complex dissociating to give the free enzyme and product
complex dissociating to give the free enzyme and product 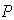 . The Michaelis-Menten equation for this system is:
. The Michaelis-Menten equation for this system is: 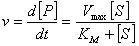 | (3) |
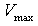 represents the maximum velocity achieved by the system, at maximum (saturating) substrate concentrations.
represents the maximum velocity achieved by the system, at maximum (saturating) substrate concentrations. 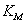 (The Michaelis constant; sometimes represented as
(The Michaelis constant; sometimes represented as 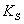 instead ) is the substrate concentration at which the reaction velocity is 50% of the
instead ) is the substrate concentration at which the reaction velocity is 50% of the 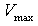 .
. 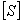 is the concentration of the substrate
is the concentration of the substrate 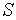 . The Michaelis-Menten equation has been used to predict the rate of product formation in enzymatic reactions for more than a century. Reuvei et al. [10] mathematically analyzed the effect of enzyme-substrate unbinding on enzymatic reactions at the single - molecule level. Tosaka et al. [11] analyzed mathematical model for oxygen diffusion in a spherical cell with Michaelis-Menten oxygen uptake kinetics by means of an integral equation method. Maalmi et al. [12] analyzed steady-state reactant diffusion followed by uptake at a small active site on a larger macromolecule or cell by Michaelis-Menten kinetics. Marchant et al. [13] described the cubic-autocatalysis with Michaelis-Menten kinetics in a one-dimensional reaction-diffusion cell. Indira et al. [14] discussed mathematical model based on catechol polyphenol oxidase as a prototype electro enzymatic system. Bucolo et al. [15] analyzed substrate removal from the extravascular compartment by Michaelis-Menten saturation type kinetics with negligible diffusion in the axial and instantaneous diffusion in the transverse directions. Do et al. [16] used the approximate analytical technique employing a finite integral transform to solve the reaction diffusion problem with Michaelis-Menten kinetics in a solid of general shape. Chapwanya and Lubuma [17] have presented the basic SIR epidemiological model with the Michaelis-Menten formulation of the contact rate. Bucolo et al. [15] analyzed the steady-state solution of the equations governing the substrate exchange between vascular and extravascular compartments separated by a membrane with finite, symmetrical substrate permeability. Napper et al. [19] discussed the Michaelis-Menten kinetics model of oxygen transport to heart tissue. A method for obtaining good approximate solutions to nonlinear diffusion-reaction boundary value problems based on the maximum principle are presented in [20]. Rajendran et al. [21] discussed mediated bioelectrocatalysis in very useful to build bioreactors, biofuel cells and biosensors. The purpose of this work is to obtain a simple closed approximate expression of concentration of substrate using the Adomian decomposition method for all values of Thiele modulus
. The Michaelis-Menten equation has been used to predict the rate of product formation in enzymatic reactions for more than a century. Reuvei et al. [10] mathematically analyzed the effect of enzyme-substrate unbinding on enzymatic reactions at the single - molecule level. Tosaka et al. [11] analyzed mathematical model for oxygen diffusion in a spherical cell with Michaelis-Menten oxygen uptake kinetics by means of an integral equation method. Maalmi et al. [12] analyzed steady-state reactant diffusion followed by uptake at a small active site on a larger macromolecule or cell by Michaelis-Menten kinetics. Marchant et al. [13] described the cubic-autocatalysis with Michaelis-Menten kinetics in a one-dimensional reaction-diffusion cell. Indira et al. [14] discussed mathematical model based on catechol polyphenol oxidase as a prototype electro enzymatic system. Bucolo et al. [15] analyzed substrate removal from the extravascular compartment by Michaelis-Menten saturation type kinetics with negligible diffusion in the axial and instantaneous diffusion in the transverse directions. Do et al. [16] used the approximate analytical technique employing a finite integral transform to solve the reaction diffusion problem with Michaelis-Menten kinetics in a solid of general shape. Chapwanya and Lubuma [17] have presented the basic SIR epidemiological model with the Michaelis-Menten formulation of the contact rate. Bucolo et al. [15] analyzed the steady-state solution of the equations governing the substrate exchange between vascular and extravascular compartments separated by a membrane with finite, symmetrical substrate permeability. Napper et al. [19] discussed the Michaelis-Menten kinetics model of oxygen transport to heart tissue. A method for obtaining good approximate solutions to nonlinear diffusion-reaction boundary value problems based on the maximum principle are presented in [20]. Rajendran et al. [21] discussed mediated bioelectrocatalysis in very useful to build bioreactors, biofuel cells and biosensors. The purpose of this work is to obtain a simple closed approximate expression of concentration of substrate using the Adomian decomposition method for all values of Thiele modulus 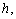 dimensionless Michaelis constant
dimensionless Michaelis constant 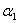 and modified Sherwood number
and modified Sherwood number 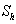 .
. 2. Mathematical Formulation of the Problem
- The problem of an enzymatic reaction occurring isothermally within a porous support particle will be considered. The shape of the particle is assumed to possess a sufficient symmetry to permit the composition at any point in space as a function of only one spatial variable (eg. slab and spherical enzyme support). The non-dimensional material balance of substrate species inside the support can be written as follows:
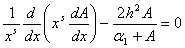 | (4) |
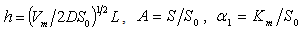 | (5) |
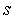 characterizes the shape of the immobilized catalyst with
characterizes the shape of the immobilized catalyst with 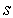 =0, 2 for slab, sphere respectively. The boundary conditions applicable to Eqn. (4) are
=0, 2 for slab, sphere respectively. The boundary conditions applicable to Eqn. (4) are 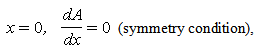 | (6) |
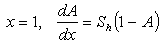 | (7) |
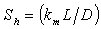 is a modified Sherwood number and
is a modified Sherwood number and 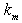 is a mass-transfer coefficient. The equation (4) can be written for slab and spherical enzyme support as follows:Case (1): Planar particle
is a mass-transfer coefficient. The equation (4) can be written for slab and spherical enzyme support as follows:Case (1): Planar particle 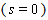 In this case the Eqn. (4) was reduces to the following dimensionless form:
In this case the Eqn. (4) was reduces to the following dimensionless form: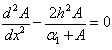 | (8) |
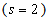 In this case the Eqn. (4) was reduces to the following dimensionless form:
In this case the Eqn. (4) was reduces to the following dimensionless form: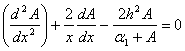 | (9) |
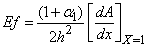 | (10) |
3. Analytical Expression of Substrate Concentration Using the Adomian Decomposition Method (ADM)
- In this paper, the Adomian decomposition method is used to solve nonlinear differential equations (8) and (9). The ADM [21-25] yields without linearization, perturbation or transformation, an analytical solution in terms of a rapidly convergent infinite power series with easily computable terms. The technique is based on a decomposition of a solution of a nonlinear operator equation in a series of functions. Each term of the series is obtained from a polynomial generated from an expansion of an analytic function in a power series. The Adomian technique is very simple in an abstract formulation, but the difficulty arises in calculating the polynomials and in proving the convergence of the series of functions. Convergence of the Adomian method when applied to some classes of ordinary and partial differential equations is discussed by many authors. For example, Abbaoui and Cherrault [26, 27] had proved the convergence of the Adomian method for differential and operator equation. The basic concept of the Adomian decomposition method is given in Appendix A. The analytical expression of concentration (Appendix B) of the substrate for planar enzyme support is as follows:
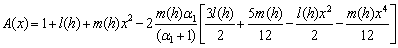 | (11) |
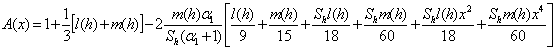 | (12) |
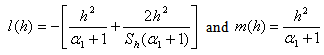 | (13) |
4. Discussion
- Eqn. (11) represents the new analytical expression of concentration of substrate
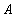 for the planar enzyme support. Concentration of substrate depends upon the parameter Thiele modulus
for the planar enzyme support. Concentration of substrate depends upon the parameter Thiele modulus 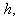 dimensionless Michaelis constant
dimensionless Michaelis constant 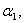 and modified Sherwood number
and modified Sherwood number 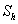 . The Thiele modulus describes the relationship between diffusion and reaction rate in porous catalyst pellets with no mass transfer limitations. This value is generally used in determining the effectiveness factor for catalyst pellets. The Thiele modulus is represented by the symbols
. The Thiele modulus describes the relationship between diffusion and reaction rate in porous catalyst pellets with no mass transfer limitations. This value is generally used in determining the effectiveness factor for catalyst pellets. The Thiele modulus is represented by the symbols 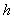 as
as 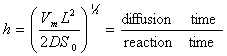 | (14) |
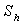 (also called the mass transfer Nusselt number) is a dimensionless number used in mass-transfer operation. It represents the ratio of convective to diffusive mass transport, and is named in honor of Thomas Kilgore Sherwood. It is defined as follows:
(also called the mass transfer Nusselt number) is a dimensionless number used in mass-transfer operation. It represents the ratio of convective to diffusive mass transport, and is named in honor of Thomas Kilgore Sherwood. It is defined as follows: 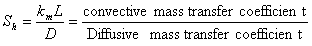 | (15) |
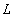 is a characteristic length (m),
is a characteristic length (m), 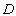 is the mass diffusivity (m2s-1),
is the mass diffusivity (m2s-1), 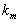 is the mass transfer coefficient (ms-1). Using dimensional analysis, it can also be further defined as a function of the Reynolds and Schmidt numbers
is the mass transfer coefficient (ms-1). Using dimensional analysis, it can also be further defined as a function of the Reynolds and Schmidt numbers 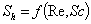 . Figures (1.a)-(1.c) represent the dimensionless concentration of substrate
. Figures (1.a)-(1.c) represent the dimensionless concentration of substrate 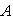 versus dimensional position X for various values of Thiele modulus
versus dimensional position X for various values of Thiele modulus 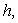 Michaelis-Menten constant
Michaelis-Menten constant 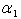 and Sherwood number
and Sherwood number 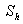 . From the figure (1.a), it is evident that the concentration of the substrate increases when
. From the figure (1.a), it is evident that the concentration of the substrate increases when 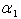 decreases. Also, the concentration is maximum at
decreases. Also, the concentration is maximum at 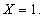 From the figures (1.b) and (1.c), it is inferred that the concentration of the substrate increases when
From the figures (1.b) and (1.c), it is inferred that the concentration of the substrate increases when 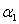 and
and 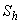 increases.
increases. 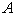 for spherical enzyme support. Figures (2.a)-(2.c) represent the dimensionless concentration of substrate
for spherical enzyme support. Figures (2.a)-(2.c) represent the dimensionless concentration of substrate 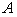 versus dimensional position X for various values of Thiele modulus
versus dimensional position X for various values of Thiele modulus 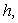 Michaelis-Menten constant
Michaelis-Menten constant 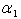 and Sherwood number
and Sherwood number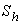 . From the figure (2.a), it is obvious that the concentration of the substrate increases when
. From the figure (2.a), it is obvious that the concentration of the substrate increases when 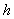 decreases. From the figures (2.b) and (2.c), it is evident that the concentration of the substrate increases when Michaelis-Menten constant
decreases. From the figures (2.b) and (2.c), it is evident that the concentration of the substrate increases when Michaelis-Menten constant 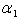 and Sherwood number
and Sherwood number 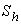 increases. The concentration of substrate attains the maximum value when
increases. The concentration of substrate attains the maximum value when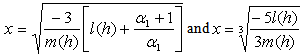 | (16) |
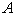 versus(a) Thiele modulus
versus(a) Thiele modulus 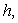 (b) dimensionless Michaelis constant
(b) dimensionless Michaelis constant 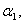 (c) modified Sherwood number
(c) modified Sherwood number 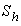 calculated using equations (11) and (12) for slab and spherical geometry respectively. All the results discussed above are confirmed in this three dimensional figures.
calculated using equations (11) and (12) for slab and spherical geometry respectively. All the results discussed above are confirmed in this three dimensional figures.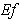 for various values of
for various values of 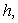
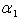 and
and 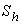 is plotted in figures (5) to (7). From the figure (5), it is inferred that the Effectiveness factor
is plotted in figures (5) to (7). From the figure (5), it is inferred that the Effectiveness factor 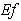 decreases when modified Sherwood number
decreases when modified Sherwood number 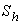 decreases for various values of
decreases for various values of 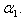 From the figure (6), it is evident that the Effectiveness factor
From the figure (6), it is evident that the Effectiveness factor 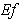 decreases for certain value and then increases when modified Sherwood number
decreases for certain value and then increases when modified Sherwood number 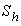 decreases for various values of
decreases for various values of 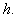 From the figure (7. a), it is obvious that the Effectiveness factor
From the figure (7. a), it is obvious that the Effectiveness factor 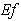 decreases when dimensionless Michaelis constant
decreases when dimensionless Michaelis constant 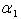 decreases. From the figure (7. b), it is evident that the Effectiveness factor
decreases. From the figure (7. b), it is evident that the Effectiveness factor 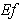 decreases for certain value and then increases when the Thiele modulus
decreases for certain value and then increases when the Thiele modulus 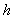 decreases.
decreases.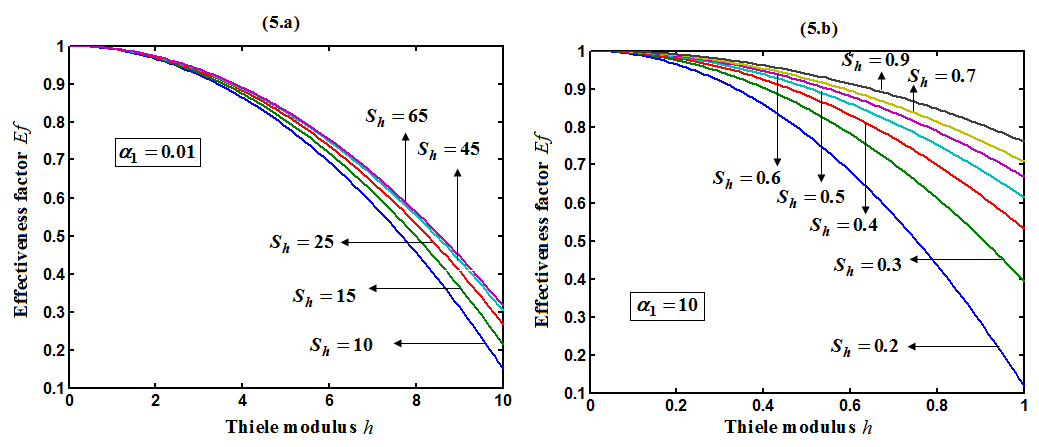 | Figure 5. Dimensionless effectiveness factor  versus Thiele modulus versus Thiele modulus  for various values of for various values of  and for the fixed value of (a) and for the fixed value of (a) 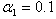 and (b) and (b) 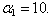 |
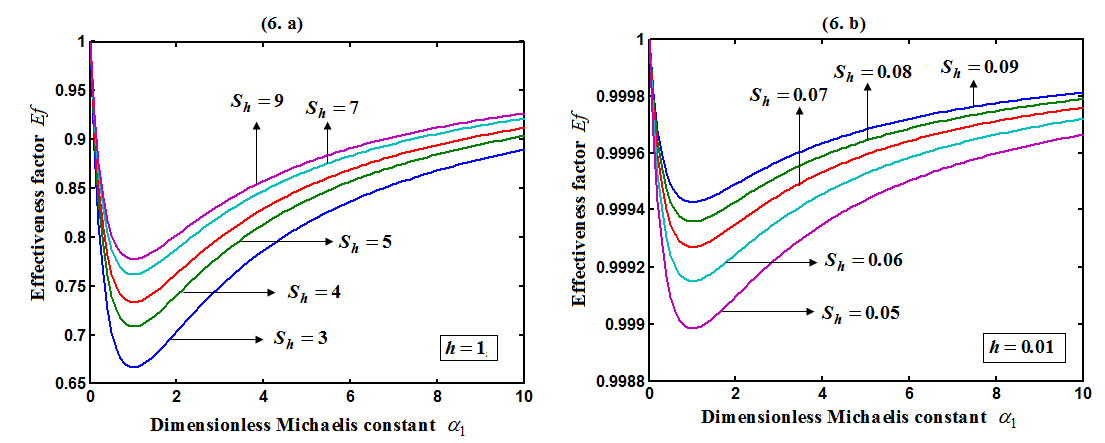 | Figure 6. Dimensionless effectiveness factor  versus dimensionless Michaelis constant versus dimensionless Michaelis constant 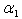 for various values of for various values of 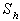 and for the fixed value of (a) and for the fixed value of (a) 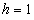 and (b) and (b) 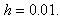 |
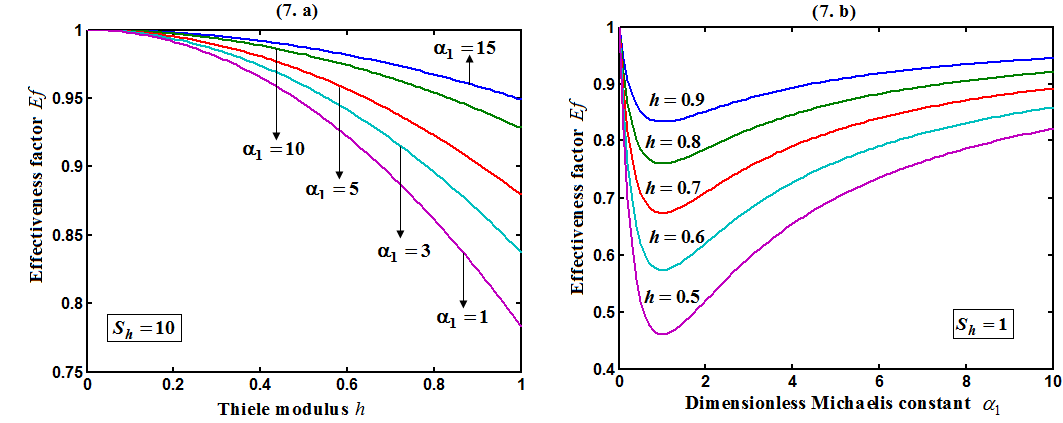 | Figure 7. Dimensionless effectiveness factor 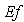 versus dimensionless (a) Thiele modulus versus dimensionless (a) Thiele modulus 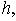 (b) Michaelis constant (b) Michaelis constant 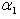 for various values of for various values of 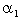 and and 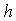 respectively respectively |
5. Conclusions
- An approximate analytical solution of the non-linear differential equation that arises from consideration of diffusion and reaction with Michaelis-Menten kinetics have been derived. Our analytical results are compared with the numerical results for various values of the Thiele modulus, the Michaelis constant and Sherwood number. Satisfactory agreement is noted. This method can be used to solve some nonlinear problems in physical and chemical sciences for various complex boundary conditions.
ACKNOWLEDGEMENTS
- This work was supported by the Department of Science and Technology (DST), Government of India. The authors also thank Mr. S. Natanagopal, Secretary, The Madura college Board, Mr. R. Murali, Principal and Department of Mathematics, The Madura College, Madurai for their encouragement.
Appendix
- Appendix ABasic concepts of the Adomian decomposition methodThe Adomian decomposition method consists of decomposing the nonlinear differential equation
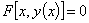 | (A.1) |
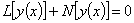 | (A.2) |
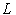 and
and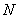 are the linear and nonlinear parts of
are the linear and nonlinear parts of 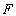 respectively. The operator
respectively. The operator 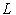 is assumed to be an invertible operator. Solving for
is assumed to be an invertible operator. Solving for 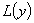 leads to
leads to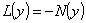 | (A.3) |
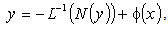 | (A.4) |
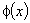 is the function that satisfies the condition
is the function that satisfies the condition 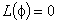 . Now suppose that the solution
. Now suppose that the solution 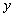 can be represented as an infinite series of the form
can be represented as an infinite series of the form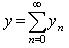 | (A.5) |
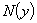 can be written as infinite series in terms of the Adomain polynomials
can be written as infinite series in terms of the Adomain polynomials 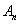 of the form
of the form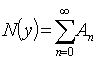 | (A.6) |
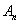 of
of 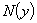 are evaluated using the formula
are evaluated using the formula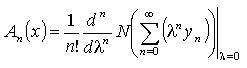 | (A.7) |
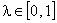 is a hypothetical parameter. Substituting Eqns. (A.5) and (A.6) in (A.4) gives
is a hypothetical parameter. Substituting Eqns. (A.5) and (A.6) in (A.4) gives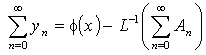 | (A.8) |
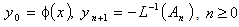 | (A.9) |
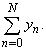 Appendix BAnalytical solutions of equation (8) using ADM (s=0)In this appendix, we derive the general solution of nonlinear Eqn. (8) by using the Adomian decomposition method. We write the Eqn. (8) in the operator form,
Appendix BAnalytical solutions of equation (8) using ADM (s=0)In this appendix, we derive the general solution of nonlinear Eqn. (8) by using the Adomian decomposition method. We write the Eqn. (8) in the operator form,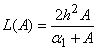 | (B.1) |
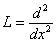 . Applying the inverse operator
. Applying the inverse operator 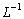 on both sides of Eqn. (B.1) yields
on both sides of Eqn. (B.1) yields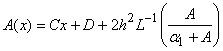 | (B.2) |
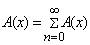 | (B.3) |
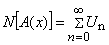 | (B.4) |
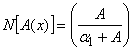 | (B.5) |
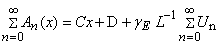 | (B.6) |
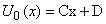 | (B.7) |
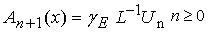 | (B.8) |
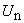 are the Adomian polynomials of
are the Adomian polynomials of 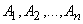 . We can find the first few
. We can find the first few 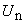 as follows:
as follows: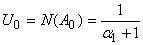 | (B.9) |
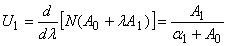 | (B.10) |
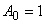 | (B.11) |
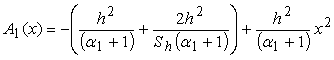 | (B.12) |
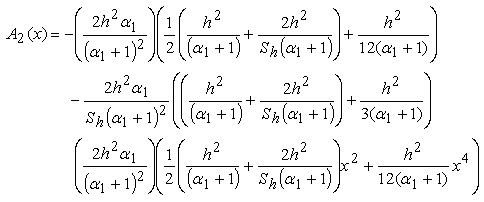 | (B.13) |
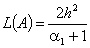 | (C.1) |
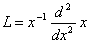 . Applying the inverse operator on both sides of Eqn. (C.1) yields
. Applying the inverse operator on both sides of Eqn. (C.1) yields 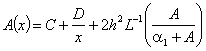 | (C.2) |
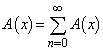 | (C.3) |
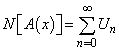 | (C.4) |
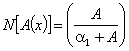 | (C.5) |
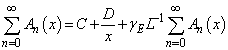 | (C.6) |
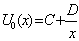 | (C.7) |
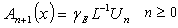 | (C.8) |
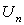 are the Adomian polynomials of
are the Adomian polynomials of 
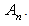 We can find the first few
We can find the first few 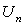 as follows:
as follows: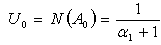 | (C.9) |
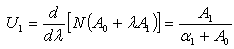 | (C.10) |
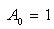 | (C.11) |
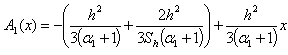 | (C.12) |
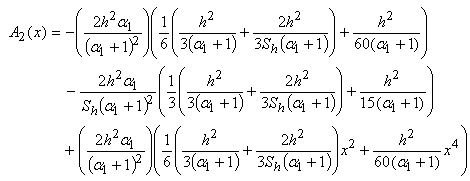 | (C.13) |

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML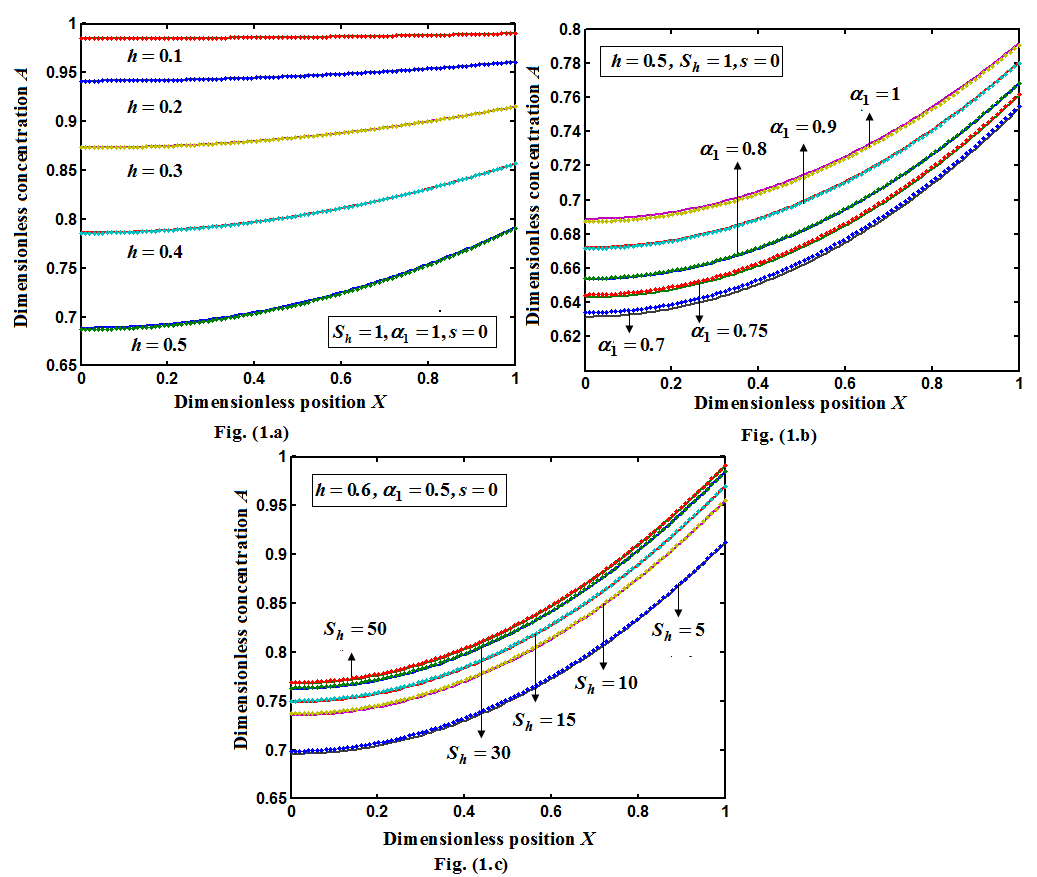
 (b) dimensionless Michaelis constant
(b) dimensionless Michaelis constant  (c) modified Sherwood number
(c) modified Sherwood number 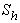 on the concentration profile of the substrate
on the concentration profile of the substrate 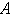 obtained in this work (equation (11)) and from the simulation result. Solid lines represent the analytical solution whereas the dotted lines in the numerical solution
obtained in this work (equation (11)) and from the simulation result. Solid lines represent the analytical solution whereas the dotted lines in the numerical solution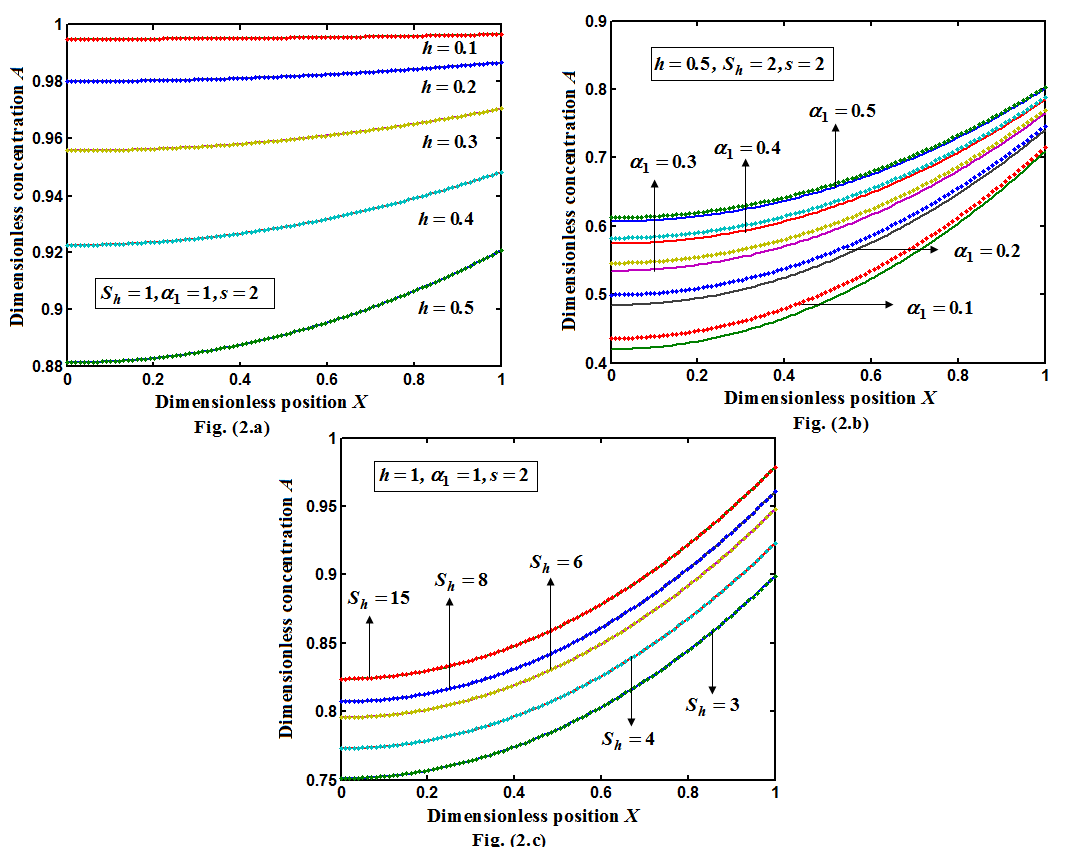
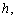 (b) dimensionless Michaelis constant
(b) dimensionless Michaelis constant 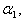 (c) modified Sherwood number
(c) modified Sherwood number 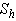 on the concentration profile of substrate
on the concentration profile of substrate 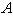 obtained in this work (equation (12)) and from the simulation result. Solid lines represent the analytical solution whereas the dotted lines in the numerical solution
obtained in this work (equation (12)) and from the simulation result. Solid lines represent the analytical solution whereas the dotted lines in the numerical solution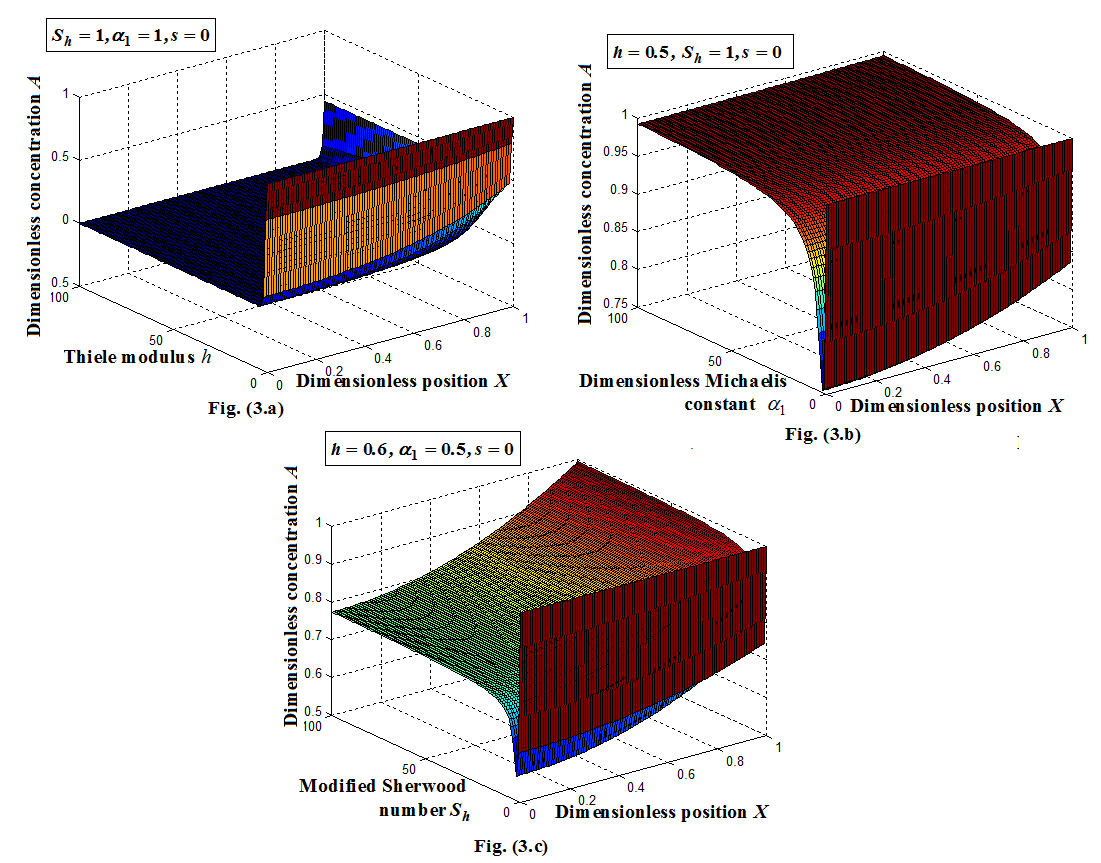
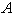 versus (a) Thiele modulus
versus (a) Thiele modulus 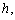 (b) dimensionless Michaelis constant
(b) dimensionless Michaelis constant 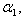 (c) modified Sherwood number
(c) modified Sherwood number 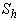 calculated using equation (11) for slab geometry
calculated using equation (11) for slab geometry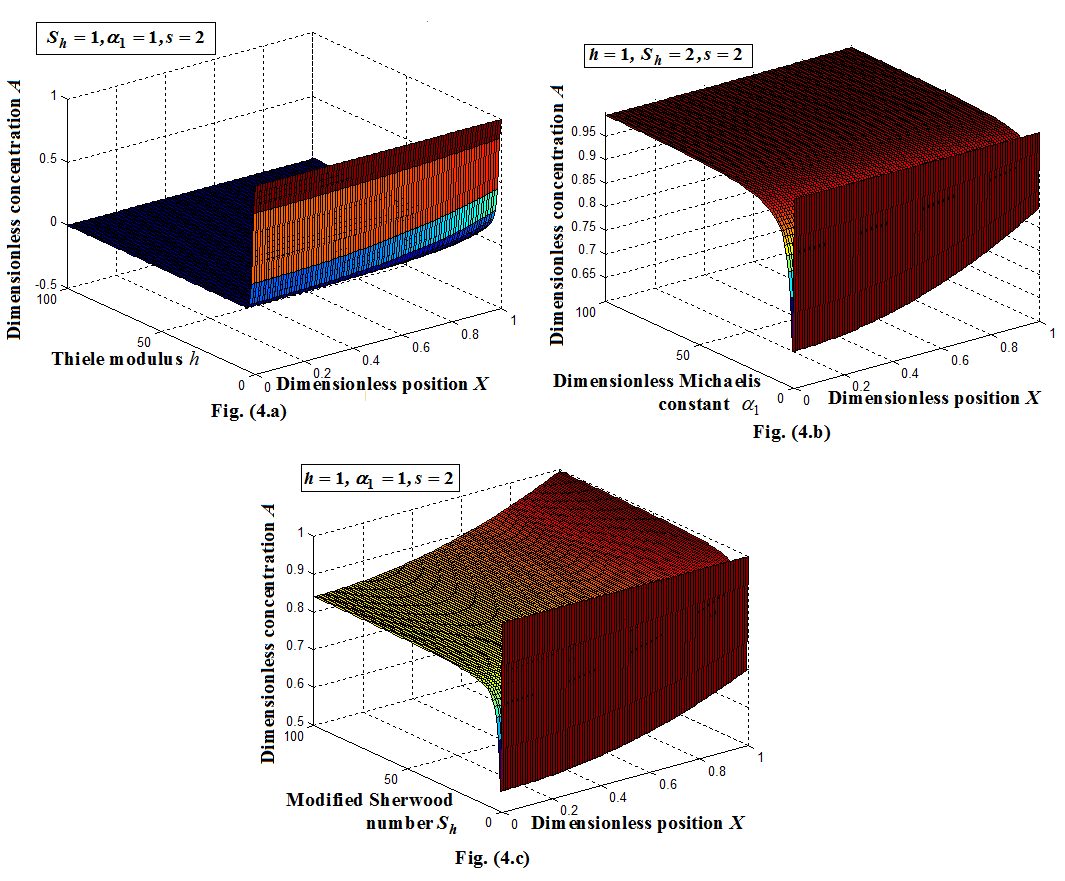
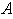 versus (a) Thiele modulus
versus (a) Thiele modulus 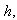 (b) dimensionless Michaelis constant
(b) dimensionless Michaelis constant  (c) modified Sherwood number
(c) modified Sherwood number 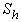 calculated using equation (12) for spherical geometry
calculated using equation (12) for spherical geometry