Waseem Asghar Khan1, Muhammad Aslam Noor2, Adnan Rauf1
1Department of Mathematics, Sukkur-Institute of Business Administration, Sukkur, Pakistan
2Department of Mathematics, COMSATS Institute of Information Technology, Islamabad, Pakistan
Correspondence to: Waseem Asghar Khan, Department of Mathematics, Sukkur-Institute of Business Administration, Sukkur, Pakistan.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we suggest and analyze a new two-step iterative method for solving nonlinear equations, which modified Noor method [6] without second derivatives for nonlinear equation. This Modified method has a fourth-order convergence and efficiency index of this method is 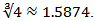 Several examples are given to illustrate the efficiency and the performance of this new method. We also present a comparison among several recent fourth-order convergent methods free from second derivatives.
Several examples are given to illustrate the efficiency and the performance of this new method. We also present a comparison among several recent fourth-order convergent methods free from second derivatives.
Keywords:
Predictor-Corrector method, Iterative method, Convergence criteria, Numerical examples
Cite this paper: Waseem Asghar Khan, Muhammad Aslam Noor, Adnan Rauf, Second Derivatives Free Fourth-Order Iterative Method Solving for Nonlinear Equation, Applied Mathematics, Vol. 5 No. 1, 2015, pp. 15-20. doi: 10.5923/j.am.20150501.03.
1. Introduction
In resent years, several iterative type methods have been developed for solving nonlinear equations 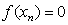 . These methods have been suggested and analyzed by using a variant of different techniques including Taylor series, decomposition and quadrature and homotopy methods, see [1-16] and the references therein for more information. Using the appropriate Taylor series expansion, we first derive an implicit type method for solving the nonlinear equations [9-16]. It is well known that to implement the implicit method, one has to use the prediction and correction type arguments. This facts motivated us to develop and suggest a two-step iterative methods. It is interesting to mention that by combining the predictor and corrector steps, we can obtain new method [6]. We would like to mention that we have to calculate the second derive of the functions, which may create some implementation problems. To overcome this drawback, we modify Noor [6] method by replacing the second derivatives of the function
. These methods have been suggested and analyzed by using a variant of different techniques including Taylor series, decomposition and quadrature and homotopy methods, see [1-16] and the references therein for more information. Using the appropriate Taylor series expansion, we first derive an implicit type method for solving the nonlinear equations [9-16]. It is well known that to implement the implicit method, one has to use the prediction and correction type arguments. This facts motivated us to develop and suggest a two-step iterative methods. It is interesting to mention that by combining the predictor and corrector steps, we can obtain new method [6]. We would like to mention that we have to calculate the second derive of the functions, which may create some implementation problems. To overcome this drawback, we modify Noor [6] method by replacing the second derivatives of the function  with new technique in [3]. In this way, we have a modified iterative method for solving nonlinear equations free from the second derivatives. This new method is robush and easy to implement. We also prove that the new modified method is of fourth-order convergence. Several examples are given to illustrate the efficiency and advantage of this two-step method.
with new technique in [3]. In this way, we have a modified iterative method for solving nonlinear equations free from the second derivatives. This new method is robush and easy to implement. We also prove that the new modified method is of fourth-order convergence. Several examples are given to illustrate the efficiency and advantage of this two-step method.
2. Iterative Methods
We consider iterative methods to find a simple root of a nonlinear equation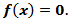 | (1) |
where 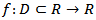 for an open interval D is a scalar function.We assume that α is simple root of the equation (1) and γ is an initial guess sufficiently close to α. Use the Taylor’s series, we have
for an open interval D is a scalar function.We assume that α is simple root of the equation (1) and γ is an initial guess sufficiently close to α. Use the Taylor’s series, we have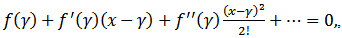 | (2) |
where γ is the initial approximation for a zero.From (2), we have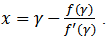 | (3) |
This allows us to suggest the following iterative method for solving the nonlinear equation (1).Algorithm 2.1. For a given x0, compute the approximate solution xn+1 by the iterative scheme.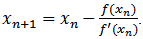 Algorithm 2.1 is the well-known Newton method and it is one-step method; which has a quadratic convergence and an efficiency index of
Algorithm 2.1 is the well-known Newton method and it is one-step method; which has a quadratic convergence and an efficiency index of  We can rewrite (2), we have
We can rewrite (2), we have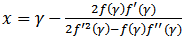 | (4) |
This formulation allows us to suggest the following an iterative method for solving the nonlinear equation (1). Algorithm 2.2: For a given x0, compute the approximate solution xn+1 by the iterative scheme.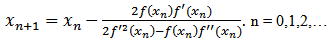 This is known as Halley’s method, which has cubic convergence [2]. The efficiency of this method is
This is known as Halley’s method, which has cubic convergence [2]. The efficiency of this method is 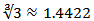 . We can rewrite the equation (2) in a different way. This alternative equivalence formula has been used to a different class of iterative methods for solving nonlinear equation
. We can rewrite the equation (2) in a different way. This alternative equivalence formula has been used to a different class of iterative methods for solving nonlinear equation 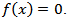
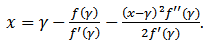 | (5) |
This fixed point formulation allows us to suggest the following method.Algorithm 2.3: For a given 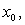 compute approximates solution
compute approximates solution 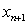 by the iterative scheme.
by the iterative scheme. 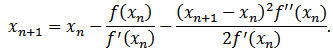 which is an implicit method, since
which is an implicit method, since 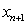 occurs on both sides. In order to implement Algorithm 2.3, Noor [6, 7] has suggested a predictor-corrector method. We use Algorithm 2.2 as a predictor and then use Algorithm 2.3 as a corrector. The Algorithm of this method is as follows:Algorithm 2.4: For a given
occurs on both sides. In order to implement Algorithm 2.3, Noor [6, 7] has suggested a predictor-corrector method. We use Algorithm 2.2 as a predictor and then use Algorithm 2.3 as a corrector. The Algorithm of this method is as follows:Algorithm 2.4: For a given 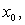 compute the approximate solution
compute the approximate solution 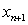 by iterative schemes.
by iterative schemes.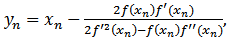 | (6) |
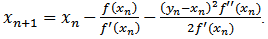 | (7) |
This is a two-step method. Algorithm 2.4 can be rewritten as:Algorithm 2.5: For a given 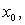 compute the approximate solution
compute the approximate solution 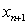 by iterative scheme.
by iterative scheme.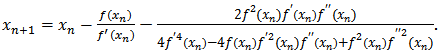 | (8) |
In order to implement this method, one has to find the second derivative of this function, which may create some problems. To overcome this drawback, one usually replaces the second order derivative by its finite difference. This technique enables us to suggest iterative method free from second derivatives. To be more precise, we the following finite difference technique: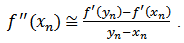 | (9) |
Combining (8) and (9), we suggest the following new iterative method for solving the nonlinear equation.Algorithm 2.6: For a given 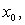 compute the approximate solution
compute the approximate solution 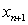 by iterative schemes.
by iterative schemes.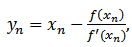 | (10) |
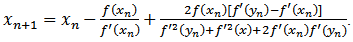 | (11) |
Recently, another approach is used to remove the second derivative from Halley’s method and some third-order iterative methods free from second derivative are obtained [3].Here, we will apply the approach use in [3] to Algorithm 2.7 and obtain a new method free from second derivative. Analysis of convergence shows that this modified method is of fourth-order convergence. And efficiency index of this method is 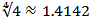 .Let
.Let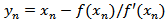 , we consider Taylor expansion of
, we consider Taylor expansion of 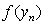 about
about 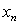
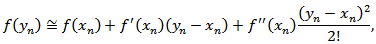 which implies
which implies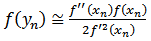 | (12) |
using (12) in (8), we obtain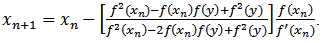 Algorithm of this method can be written as followsAlgorithm 2.7: For a given
Algorithm of this method can be written as followsAlgorithm 2.7: For a given 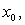 compute the approximate solution
compute the approximate solution 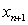 by iterative schemes.
by iterative schemes.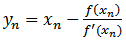 | (13) |
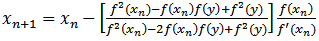 | (14) |
This method does not require the second derivative. Important characteristic of this method is that per iteration they require two evaluations of the function and one of its first derivatives. The efficiency of this method is 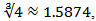 which is better than that of the well-known other methods involving the second-order derivative of the function. We recall these methods for the sake of completeness.Kou et al. [4] have suggested a foruth-order methods. The Algorithm of these fourth-order methods can be written as follows:Algorithm 2.8: (K1, [4]) For a given
which is better than that of the well-known other methods involving the second-order derivative of the function. We recall these methods for the sake of completeness.Kou et al. [4] have suggested a foruth-order methods. The Algorithm of these fourth-order methods can be written as follows:Algorithm 2.8: (K1, [4]) For a given 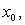 compute the approximate solution
compute the approximate solution 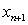 by iterative scheme.
by iterative scheme.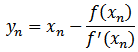
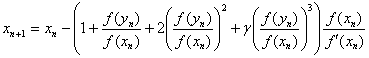 .
. 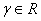 .Noor and V. Gupta [5] have suggested a iterative method of fourth-order. The Algorithm of this method can be written as follows:Algorithm 2.9: (NR, [5]) For a given
.Noor and V. Gupta [5] have suggested a iterative method of fourth-order. The Algorithm of this method can be written as follows:Algorithm 2.9: (NR, [5]) For a given 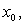 compute the approximate solution
compute the approximate solution 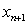 by iterative scheme.
by iterative scheme.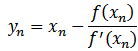
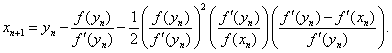
3. Convergence Criteria
Now we consider the convergence criteria of Algorithm 2.7.Theorem 1: Let 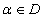 be a simple zero of sufficiently differentiable function
be a simple zero of sufficiently differentiable function 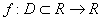 for an open interval
for an open interval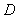 . If
. If 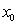 is sufficiently close to
is sufficiently close to 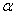 , then Algorithm 2.7 has fourth-order convergences.Proof.If
, then Algorithm 2.7 has fourth-order convergences.Proof.If 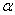 is the root and
is the root and 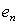 be the error at nth iteration, than
be the error at nth iteration, than 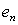 =
= 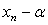 , using Taylor’s expansion, we have
, using Taylor’s expansion, we have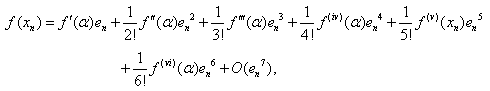 | (15) |
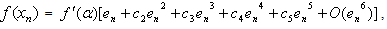 | (16) |
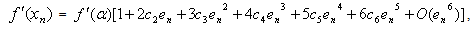 | (17) |
where 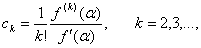 let
let 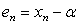 .From (16) and (17), we have
.From (16) and (17), we have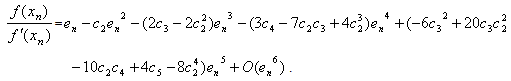 | (18) |
Using (18) in (13), we obtain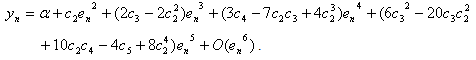 | (19) |
From (19), we have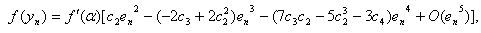 | (20) |
from (16) and (20), we obtain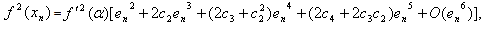 | (21) |
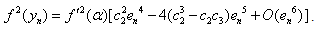 | (22) |
Adding (21) and (22), we obtain 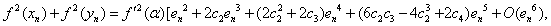 | (23) |
from (16) and (20), we have 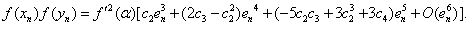 | (24) |
Subtracting (23) and (24), we obtain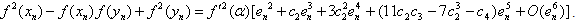 | (25) |
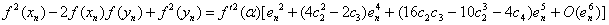 | (26) |
Dividing (25) and (26), we obtain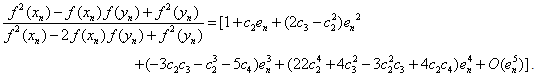 | (27) |
Using (18) and (27), we have 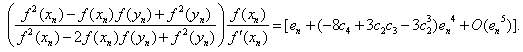 | (28) |
Put (28) in (14), we obtain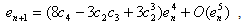 which shows that Algorithm 2.7 has fourth-order convergence.
which shows that Algorithm 2.7 has fourth-order convergence.
4. Numerical Examples
We present some examples to illustrate the efficiency of the new developed iterative methods. We compare the Newton method (NM), Noor method (NR, [5]), method of Kou (K1, [4]), method of Algorithm 2.6 (N1, [6]), and new method Algorithm 2.7. We used 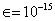 . The following stopping criteria are used for computer programs:(i)
. The following stopping criteria are used for computer programs:(i) 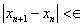 .(ii)
.(ii) 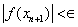 .The examples are the same as in Chun [1].
.The examples are the same as in Chun [1].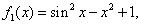
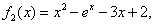
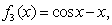
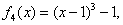
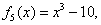
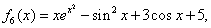
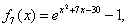
Table 1. Numerical comparison
 |
| |
|
5. Conclusions
We have shown that it is possible to obtain modifications of Noor [6] method free from second derivative by using a new approach to remove the second derivative from Noor method. We prove that the order of convergence of this method is four. Analysis of efficiency shows that this method is preferable to the well-known other methods involving the second order derivative of the function. Numerical results show that these methods have definite practical utility.
ACKNOWLEDGEMENTS
The authors are grateful to Dean & Rector Nisar Ahmed Siddiqui, Institute of Business Administration, Sukkur for providing excellent research environment and facilities.
References
| [1] | C. Chun, Iterative methods improving Newton’s method by the decomposition method, Comput. Math. Appl. 50 (2005) 1559-1568. |
| [2] | T. Fang, F. Guo, C. F. Lee, A new iterative methods with cubic convergence to solve nonlinear algebraic equations, Appl. Math. and Comput. 175 (2006) 1147- 1155. |
| [3] | J. S. Kou, Y. T. Li, X. H. Wang, Modified Halley,s method free from second derivative, Appl. Math. Comput. (2006), in press. |
| [4] | J. Kou, Second-derivative-free variants of Cauchy,s method, Appl. Math.Comput. (2007) in press. |
| [5] | M. Aslam Noor, V. Gupta, Modified Householder iterative method free from second derivatives for nonlinear equations, Appl. Math. Comput., (2007), in press. |
| [6] | M. Aslam Noor, W. A. Khan, Third-order predictor-corrector method for solving nonlinear equation, International conference on Mathematics in Malaysia Proceeding. 772-782. |
| [7] | W. A. Khan, Numerical Analysis and Computation, Lecture Notes, Sukkur Institute of Business Administration, Sukkur, Pakistan, 2014 |
| [8] | J. F. Traub, Iterative methods for the solution of equations, prentice Hall, Englewood Cliffs (NJ), 1964. |
| [9] | W. A. Khan, Numerical Analysis and Computation, Lecture Notes, Department of Mathematics, Sukkur-IBA, 2013. |
| [10] | M. A. Noor, W. A. Khan, Fourth-Order Iterative Method Free from Second Derivative for Solving Nonlinear Equations, Appl. Math. Sci., Vol. 6, 2012, no. 93, 4617 – 4625. |
| [11] | M. A. Noor, W. A. Khan, New iterative methods for solving nonlinear equation by using homotopy perturbation method, Appl. Math. Comput., 219 (2012) pp. 3565-3574 |
| [12] | M. A. Noor, W. A. Khan, K. I. Noor, E. Al-Said (2011). Higher-order iterative methods free from second derivative for solving nonlinear equations. Int. J. Phy. Sci. 6(8): 1887-1897. |
| [13] | M. A. Noor, W. A. Khan, A. Hussain (2007). A new modified Halley method without second derivatives for nonlinear equation. Appl. Math. Compu. 189: 1268-1273. |
| [14] | W. A. Khan, M. A. Noor, S. Younus, Homotopy perturbation techniques for the solution of certain nonlinear equations. Appl. Math. Sci., Vol. 6, 2012, no. 130, 6487 – 6499. |
| [15] | M. A. Noor, K. I Noor, W. A. Khan and F. Ahmad, On iterative methods for nonlinear equations, Appl. Math. Comput., 183 (2006) 128-133. |
| [16] | W. A. Khan, M. A. Noor, A. Rauf, Higher-order iterative methods by using Householders method for solving certain nonlinear equations, Vol 2, No. 2, (2013) pp 107-120. |
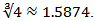 Several examples are given to illustrate the efficiency and the performance of this new method. We also present a comparison among several recent fourth-order convergent methods free from second derivatives.
Several examples are given to illustrate the efficiency and the performance of this new method. We also present a comparison among several recent fourth-order convergent methods free from second derivatives.
 . These methods have been suggested and analyzed by using a variant of different techniques including Taylor series, decomposition and quadrature and homotopy methods, see [1-16] and the references therein for more information. Using the appropriate Taylor series expansion, we first derive an implicit type method for solving the nonlinear equations [9-16]. It is well known that to implement the implicit method, one has to use the prediction and correction type arguments. This facts motivated us to develop and suggest a two-step iterative methods. It is interesting to mention that by combining the predictor and corrector steps, we can obtain new method [6]. We would like to mention that we have to calculate the second derive of the functions, which may create some implementation problems. To overcome this drawback, we modify Noor [6] method by replacing the second derivatives of the function
. These methods have been suggested and analyzed by using a variant of different techniques including Taylor series, decomposition and quadrature and homotopy methods, see [1-16] and the references therein for more information. Using the appropriate Taylor series expansion, we first derive an implicit type method for solving the nonlinear equations [9-16]. It is well known that to implement the implicit method, one has to use the prediction and correction type arguments. This facts motivated us to develop and suggest a two-step iterative methods. It is interesting to mention that by combining the predictor and corrector steps, we can obtain new method [6]. We would like to mention that we have to calculate the second derive of the functions, which may create some implementation problems. To overcome this drawback, we modify Noor [6] method by replacing the second derivatives of the function  with new technique in [3]. In this way, we have a modified iterative method for solving nonlinear equations free from the second derivatives. This new method is robush and easy to implement. We also prove that the new modified method is of fourth-order convergence. Several examples are given to illustrate the efficiency and advantage of this two-step method.
with new technique in [3]. In this way, we have a modified iterative method for solving nonlinear equations free from the second derivatives. This new method is robush and easy to implement. We also prove that the new modified method is of fourth-order convergence. Several examples are given to illustrate the efficiency and advantage of this two-step method.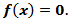
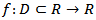 for an open interval D is a scalar function.We assume that α is simple root of the equation (1) and γ is an initial guess sufficiently close to α. Use the Taylor’s series, we have
for an open interval D is a scalar function.We assume that α is simple root of the equation (1) and γ is an initial guess sufficiently close to α. Use the Taylor’s series, we have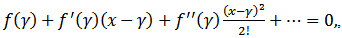
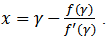
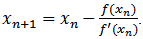 Algorithm 2.1 is the well-known Newton method and it is one-step method; which has a quadratic convergence and an efficiency index of
Algorithm 2.1 is the well-known Newton method and it is one-step method; which has a quadratic convergence and an efficiency index of 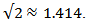 We can rewrite (2), we have
We can rewrite (2), we have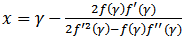
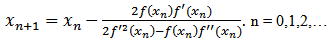 This is known as Halley’s method, which has cubic convergence [2]. The efficiency of this method is
This is known as Halley’s method, which has cubic convergence [2]. The efficiency of this method is 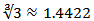 . We can rewrite the equation (2) in a different way. This alternative equivalence formula has been used to a different class of iterative methods for solving nonlinear equation
. We can rewrite the equation (2) in a different way. This alternative equivalence formula has been used to a different class of iterative methods for solving nonlinear equation 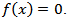
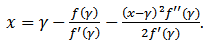
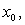 compute approximates solution
compute approximates solution 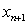 by the iterative scheme.
by the iterative scheme. 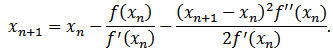 which is an implicit method, since
which is an implicit method, since 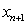 occurs on both sides. In order to implement Algorithm 2.3, Noor [6, 7] has suggested a predictor-corrector method. We use Algorithm 2.2 as a predictor and then use Algorithm 2.3 as a corrector. The Algorithm of this method is as follows:Algorithm 2.4: For a given
occurs on both sides. In order to implement Algorithm 2.3, Noor [6, 7] has suggested a predictor-corrector method. We use Algorithm 2.2 as a predictor and then use Algorithm 2.3 as a corrector. The Algorithm of this method is as follows:Algorithm 2.4: For a given 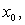 compute the approximate solution
compute the approximate solution 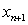 by iterative schemes.
by iterative schemes.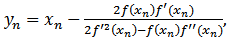
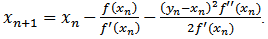
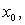 compute the approximate solution
compute the approximate solution 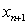 by iterative scheme.
by iterative scheme.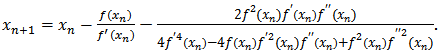
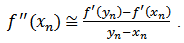
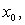 compute the approximate solution
compute the approximate solution 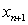 by iterative schemes.
by iterative schemes.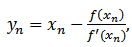
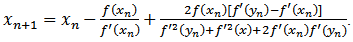
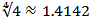 .Let
.Let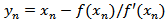 , we consider Taylor expansion of
, we consider Taylor expansion of 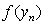 about
about 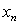
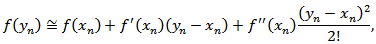 which implies
which implies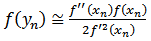
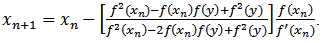 Algorithm of this method can be written as followsAlgorithm 2.7: For a given
Algorithm of this method can be written as followsAlgorithm 2.7: For a given 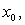 compute the approximate solution
compute the approximate solution 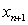 by iterative schemes.
by iterative schemes.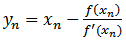
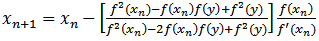
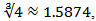 which is better than that of the well-known other methods involving the second-order derivative of the function. We recall these methods for the sake of completeness.Kou et al. [4] have suggested a foruth-order methods. The Algorithm of these fourth-order methods can be written as follows:Algorithm 2.8: (K1, [4]) For a given
which is better than that of the well-known other methods involving the second-order derivative of the function. We recall these methods for the sake of completeness.Kou et al. [4] have suggested a foruth-order methods. The Algorithm of these fourth-order methods can be written as follows:Algorithm 2.8: (K1, [4]) For a given 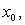 compute the approximate solution
compute the approximate solution 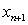 by iterative scheme.
by iterative scheme.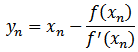
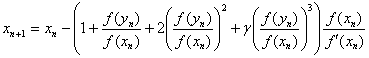 .
. 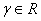 .Noor and V. Gupta [5] have suggested a iterative method of fourth-order. The Algorithm of this method can be written as follows:Algorithm 2.9: (NR, [5]) For a given
.Noor and V. Gupta [5] have suggested a iterative method of fourth-order. The Algorithm of this method can be written as follows:Algorithm 2.9: (NR, [5]) For a given 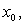 compute the approximate solution
compute the approximate solution 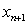 by iterative scheme.
by iterative scheme.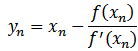
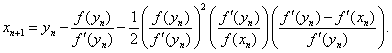
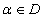 be a simple zero of sufficiently differentiable function
be a simple zero of sufficiently differentiable function 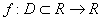 for an open interval
for an open interval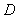 . If
. If 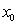 is sufficiently close to
is sufficiently close to 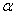 , then Algorithm 2.7 has fourth-order convergences.Proof.If
, then Algorithm 2.7 has fourth-order convergences.Proof.If 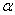 is the root and
is the root and 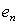 be the error at nth iteration, than
be the error at nth iteration, than 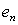 =
= 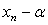 , using Taylor’s expansion, we have
, using Taylor’s expansion, we have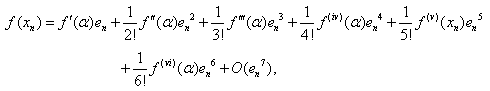
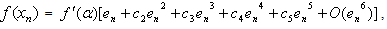
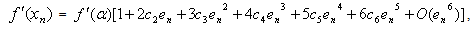
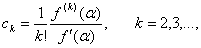 let
let 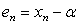 .From (16) and (17), we have
.From (16) and (17), we have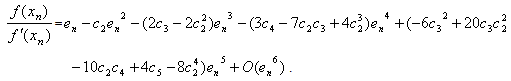
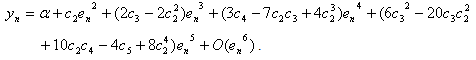
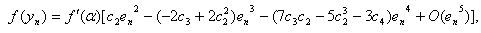
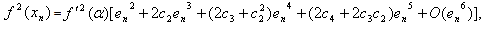
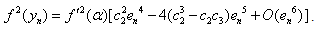
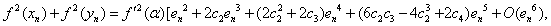
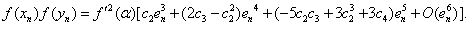
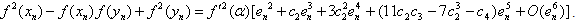
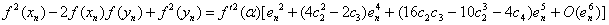
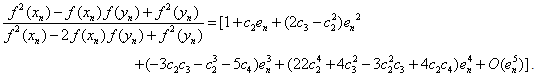
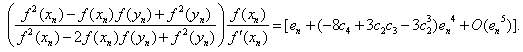
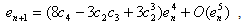 which shows that Algorithm 2.7 has fourth-order convergence.
which shows that Algorithm 2.7 has fourth-order convergence. 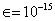 . The following stopping criteria are used for computer programs:(i)
. The following stopping criteria are used for computer programs:(i) 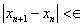 .(ii)
.(ii) 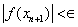 .The examples are the same as in Chun [1].
.The examples are the same as in Chun [1].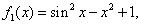
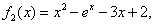
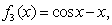
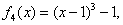
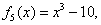
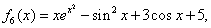
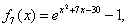
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML