Bright O. Osu1, Joy I. Adindu-Dick2
1Department of Mathematics, Abia State University, Uturu, Nigeria
2Department of Mathematics, Imo State University, Nigeria
Correspondence to: Bright O. Osu, Department of Mathematics, Abia State University, Uturu, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We studied the rate of returns on investment as the net gain in wealth over the cumulative investment in continuous time. Dynamic asset allocations are continuously rebalanced so as to always keep a fixed constant proportion of wealth invested in various assets at each point in time play a fundamental role in the theory of optimal portfolio strategy. We proved that: (i) the limiting distribution of this measure of return is gamma distribution if the returns follow a geometric Brownian motion; (ii) if returns follow Weibull distribution, then it results to asymptotic power-law behavior of assets returns. For example, the mean return on investment is maximized by the same strategy that maximizes logarithm utility which is also known to minimize the exponential rate at which wealth grows and the return from this policy turns out to have stochastic dominance properties as well. We consider the logistic function in large market financial crashes corresponding to values of packing dimension of  by the fractal dispersion of Hausdorff measure prior to market signal with constraint of a zero heat capacity, the existence of a unique solution to the associated Hausdorff is established and optimal policy is characterized. Also advocated is a procedure for locating optimal market crises signal relative to the heat equation to give an early warning.
by the fractal dispersion of Hausdorff measure prior to market signal with constraint of a zero heat capacity, the existence of a unique solution to the associated Hausdorff is established and optimal policy is characterized. Also advocated is a procedure for locating optimal market crises signal relative to the heat equation to give an early warning.
Keywords:
Optimal policy, Contingent claim, Power Law, Hausdorff measure, Market signal, Fractal dispersion
Cite this paper: Bright O. Osu, Joy I. Adindu-Dick, Optimal Policy on the Possible Rate of Returns of Contingent Claim by Fractal Dispersion on Hausdorff Measure to Market Signal, Applied Mathematics, Vol. 5 No. 1, 2015, pp. 1-6. doi: 10.5923/j.am.20150501.01.
1. Introduction
Ethier et al, [2] studied the rate of return on investment in discrete time gambling method, where the total return on the individual gambler is assumed to follow a random walk. They also showed that the asymptotic distribution of the return, as the mean increment in the random walk goes to zero is a gamma distribution. Also Kelly (1956) in Thorp, [11] observed the relationship between the logarithm of wealth and expected asymptotic rate at which wealth compounds. The object is to let one know how one should invest in each equities of ones highly diversified stocks portfolio to maximize the capital growth. In finance, the rate of return (ROR) which is known as return on investment (ROI) is the ratio of money gained or lost whether realized or unrealized on an investment, relative to the amount of money invested. The amount of money gained or lost may be referred to as interest, profit/loss, gain/loss or net income/loss. There are several ways to determine ROI, but the most frequently used method is net gain divided by total assets. Constant proportions investment strategies also play a fundamental role in portfolio theory. Under these policies, an investor follows a dynamic trading strategy that continually rebalances the portfolio so as to always allocate fixed constant proportions of the investor’s wealth across the investment opportunities. These strategies are widely used in practice and are also referred to as continuously rebalanced strategy [9]. Given the fundamental nature of policies in theoretical portfolio practice, it is of interest to know what the stochastic behavior of the rate of return on investment (RROI), defined as the net of gain over the cumulative investment [3]. Merton, [5] introduced the setting in the continuous time financial model as used in Black-Scholes, [1].In this paper, we obtain some limit theorems for RROI which allows us to compare and derive some specific optimality properties for certain portfolio strategies. We also established and proved that the return on investment for such policies converges to a limiting stochastic distribution and the result provides a basis upon which to compare different strategies on Hausdorff measure prior to the heat equation to locate market crises and give early warning.
2. The Rate of Return from Total Investment
The rate of return on investment is defined as the ratio of net gain in wealth over the cumulative investment. Our interest here is the rate of return from the total investment (RROI), which for the fixed policy will be denoted by the process  Hence
Hence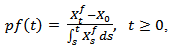 | (2.1) |
which is equivalent to the least square estimator 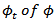 studied by Hu, et al [4] on the continuous parametric estimation of observed fractional Ornstein-Uhlenbeck process
studied by Hu, et al [4] on the continuous parametric estimation of observed fractional Ornstein-Uhlenbeck process 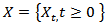 defined as
defined as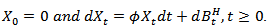 | (2.2) |
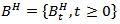 is a fractional Brownian motion with Hurst parameter
is a fractional Brownian motion with Hurst parameter 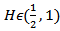 given as
given as 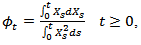 | (2.3) |
Where  is a measure of the wealth it takes to finance a gain. If
is a measure of the wealth it takes to finance a gain. If  is large; it means that the investor is accumulating gains at a faster rate than if it is small. Note that if we divide the numerator and the denominator by t in equation (2.1) we also interpret
is large; it means that the investor is accumulating gains at a faster rate than if it is small. Note that if we divide the numerator and the denominator by t in equation (2.1) we also interpret  as the average net gain over the average wealth level.Theorem 2.1If the returns of contingent claim
as the average net gain over the average wealth level.Theorem 2.1If the returns of contingent claim 
 follow geometric Brownian motion
follow geometric Brownian motion 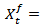
 , then the resulting distribution is Gamma distribution, that is,
, then the resulting distribution is Gamma distribution, that is, 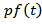
 ProofRecall that
ProofRecall that 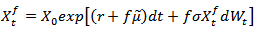 then
then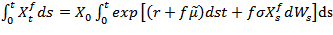 | (2.4) |
From geometric Brownian motion,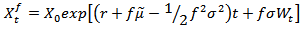 | (2.5) |
and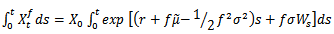 | (2.6) |
Substitute (2.5) and (2.6) in (2.1) to get which implies
which implies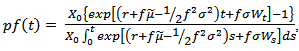 and simplifies to
and simplifies to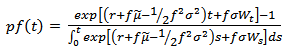 | (2.7) |
If  we have that from equation (2.7) it shows that for that policy under which the total wealth is always invested in the risk-free asset is
we have that from equation (2.7) it shows that for that policy under which the total wealth is always invested in the risk-free asset is 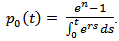 But
But  so that
so that If
If 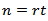 then
then  is the risk free interest rate as expected but if
is the risk free interest rate as expected but if 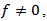 the rate of return on investment (RROI) process
the rate of return on investment (RROI) process 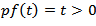 is complicated and does not yield to a simple direct analysis.NOTE: a random variable
is complicated and does not yield to a simple direct analysis.NOTE: a random variable 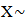 gamma
gamma  means that X is a random variable with density function
means that X is a random variable with density function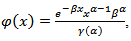 with
with  and the
and the  And for any fixed proportion that satisfies
And for any fixed proportion that satisfies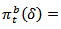
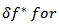 all
all  , the (RROI) process
, the (RROI) process converges
converges 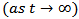 in distribution to random variable which has a gamma distribution, where
in distribution to random variable which has a gamma distribution, where 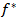 is the constant vector given by
is the constant vector given by 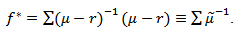 If
If  is a constant vector for all
is a constant vector for all  such a policy is called constant proportion policy which is the optimal investment policy for any interesting objective function. A constant vector is also optimal policy for other objective criteria, such as minimizing the expected time t to reach a given level of wealth as well.Specifically, as
such a policy is called constant proportion policy which is the optimal investment policy for any interesting objective function. A constant vector is also optimal policy for other objective criteria, such as minimizing the expected time t to reach a given level of wealth as well.Specifically, as 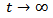 we have
we have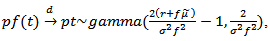 | (2.8) |
where  denotes convergence in distribution.Therefore to get the expectation of
denotes convergence in distribution.Therefore to get the expectation of  we have
we have 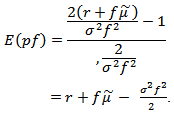 | (2.9) |
The expectation in (2.9) should not be confused with the ratio of the expected gain to the expected total investment which for any  is equal to
is equal to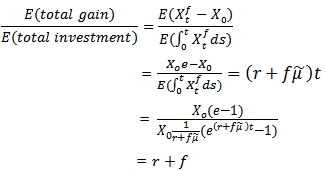 | (2.10) |
Theorem 2.2If the returns  as defined in (2.1) follow Weibull randomvariates
as defined in (2.1) follow Weibull randomvariates , then the resulting distribution
, then the resulting distribution  follows asymptotic power-law.ProofLet
follows asymptotic power-law.ProofLet 
 be distributed according to the following probability density function
be distributed according to the following probability density function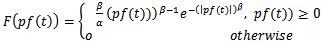 | (2.11) |
where  are the mean and the shape parameters of the Weibull distribution (2.11).If
are the mean and the shape parameters of the Weibull distribution (2.11).If 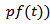 has the Weibull density function, then
has the Weibull density function, then  has the exponential density function with
has the exponential density function with  as (using the formula in [7]);
as (using the formula in [7]);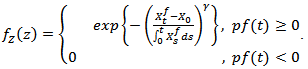 | (2.12) |
Thus the optimal investment strategy is (see [8]);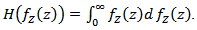 | (2.13) |
That is 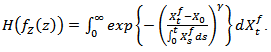 | (2.14) |
But  (where
(where  is as in (2.4) or (2.6)), so that
is as in (2.4) or (2.6)), so that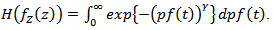 Hence the optimal strategy is the asymptotic power-law;
Hence the optimal strategy is the asymptotic power-law;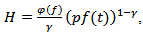 | (2.15) |
where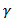 is the fractal exponent given by (see [6])
is the fractal exponent given by (see [6])  with
with  a Bessel function given as
a Bessel function given as 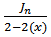 and
and 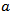 the singularity strength
the singularity strength 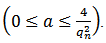
3. Optimal Growth Policy and Stochastic Dominance
Here we can see that the quantity (2.8) is maximized by the strategy that invests as much as possible in the risky asset. The mean of (2.7), is maximized at a finite value 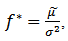 | (3.1) |
which is the same policy that is optimal for maximizing logarithmic utility of wealth at a fixed terminal time and hence for maximizing exponential rate of growth. Notice that the mean of the limiting distribution of (RROI) process is maximized at the value  with resulting mean
with resulting mean  for this strategy the RROI,
for this strategy the RROI,  satisfies
satisfies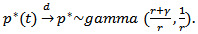 | (3.2) |
In fact, the distribution characterization of the limiting RROI allows for some-what stronger statement, in terms of stochastic orderings. Suppose that for two random variables, X,Y we say that 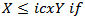
 This is equivalent to say that
This is equivalent to say that  for all increasing convex function
for all increasing convex function  and is referred to as the increasing convex ordering. We also say that (provided the expectations are finite) this is equivalent to saying that
and is referred to as the increasing convex ordering. We also say that (provided the expectations are finite) this is equivalent to saying that  for all increasing concave function
for all increasing concave function 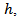 and is hence referred to as the increasing concave ordering.We let
and is hence referred to as the increasing concave ordering.We let  denote the RRIO obtained from using the policy
denote the RRIO obtained from using the policy  defined in (2.9) and let
defined in (2.9) and let  be the RROI. From any other constant proportion strategy
be the RROI. From any other constant proportion strategy  where c is an arbitrary constant, the following hold
where c is an arbitrary constant, the following hold Equation (a) is in effect for investor with greater relative risk aversion while equation (b) is in effect for an investor with less relative risk aversion. Then for a proportional strategy
Equation (a) is in effect for investor with greater relative risk aversion while equation (b) is in effect for an investor with less relative risk aversion. Then for a proportional strategy  where
where  is the optimal policy of (2.7), the relationship
is the optimal policy of (2.7), the relationship  holds if and only if C satisfies
holds if and only if C satisfies 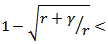
 Showing that the only type of constant proportion policy (other than
Showing that the only type of constant proportion policy (other than  for which RROI is stochastically dominated by the optimal growth policy is one that is shorting the stock to the degree required by
for which RROI is stochastically dominated by the optimal growth policy is one that is shorting the stock to the degree required by  To establish equation (2.1) in section 1 above, we have that the process
To establish equation (2.1) in section 1 above, we have that the process 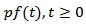 does not admit a simple direct analysis, there is a related markov process amenable to analysis which holds the key for the limiting behavior of
does not admit a simple direct analysis, there is a related markov process amenable to analysis which holds the key for the limiting behavior of  specifically the
specifically the  0 defined by
0 defined by 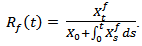 | (3.3) |
If t = 0 we have  also we will first show that the limiting behavior of
also we will first show that the limiting behavior of  is equivalent to the limiting behavior of
is equivalent to the limiting behavior of  But our interest here is to show the limiting behavior of the RROI process
But our interest here is to show the limiting behavior of the RROI process  We show that the diffusion process
We show that the diffusion process 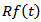 whose limiting behavior can be analyzed.Suppose that for random variable
whose limiting behavior can be analyzed.Suppose that for random variable  we have
we have 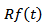
 Then for any
Then for any we have
we have 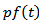
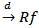
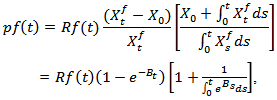 | (3.4) |
where 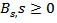 is the linear Brownian motion defined by
is the linear Brownian motion defined by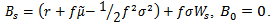 Note that
Note that  hasa positive drifts which implies that
hasa positive drifts which implies that as well as
as well as  Equation (2.1) will be completely establish if we can prove that
Equation (2.1) will be completely establish if we can prove that  for some random variable
for some random variable  with
with  Lemma 3.1: For some fixed proportion investment policy
Lemma 3.1: For some fixed proportion investment policy  the process
the process  follows the stochastic differential equation
follows the stochastic differential equation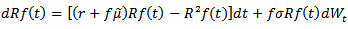 | (3.5) |
 is a temporary homogeneous diffusion process with drift function
is a temporary homogeneous diffusion process with drift function  and diffusion function
and diffusion function ProofLet
ProofLet  be the cumulative wealth investment process, also let
be the cumulative wealth investment process, also let  Since
Since  is a process of bounded variation, its Ito’s rule show that
is a process of bounded variation, its Ito’s rule show that  so applying Ito’s rule to
so applying Ito’s rule to 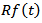 gives
gives 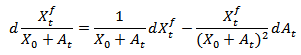 which upon substitution gives
which upon substitution gives 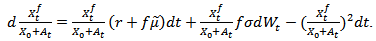 | (3.6) |
The result is equivalent to (3.5). Here, the policy is maximized by a strategy that invests as much as possible in the risky asset and the total return from this policy turns out to have stochastic dominance property as well. This continuous stochastic process can be used for modeling random behavior that evolves over time like fluctuation in an asset price.
4. Application on Logistic Financial Fractal Dispersion Function of the Hausdorff Priorto Crash Market Signal
One of the several distinct techniques of investigating the size of subsets of zero market in  is the notion of packing dimension due to Taylor and Triort, [10].Packing dimension is defined via the packing measure as a class φ of monotone functions h
is the notion of packing dimension due to Taylor and Triort, [10].Packing dimension is defined via the packing measure as a class φ of monotone functions h 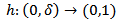 which is non decreasing, right continuous satisfying h(0+) = 0 and for which there is a constant.
which is non decreasing, right continuous satisfying h(0+) = 0 and for which there is a constant.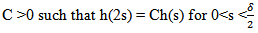 | (4.1) |
We obtain the packing dimension by two definitions. First, we defined a pre-measure 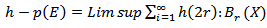 | (4.2) |
disjoint  Where
Where  denotes the open ball centered on X radius r Eq(4.2) is not an outer measure because it is not count ably Sub-additive. However it leads to an outer measure by defining
denotes the open ball centered on X radius r Eq(4.2) is not an outer measure because it is not count ably Sub-additive. However it leads to an outer measure by defining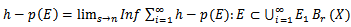 | (4.3) |
which can be thought of as a generalization of Hausdorff measure using maximal packing of E by balls, so that if h(s) 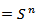 then h –p( ) on
then h –p( ) on 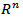 is n-dimensional Hausdorff measure. Thus to measure the Borel subset of
is n-dimensional Hausdorff measure. Thus to measure the Borel subset of  we need
we need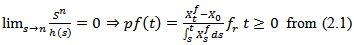 | (4.4) |
So that if  there is a unique value of
there is a unique value of  for which the packing measure h- P(E) drops from infinity to zero.This in turn means that E is less occupied than if it were
for which the packing measure h- P(E) drops from infinity to zero.This in turn means that E is less occupied than if it were  dimensional. For
dimensional. For  We define the next Dim E as
We define the next Dim E as 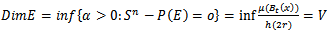 | (4.5) |
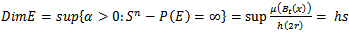 | (4.6) |
which denotes the packing dimension E.The underlying assets is paying nontrivial continuous dividends with an annualized yield  A holder of the underlying asset receives a dividends yield
A holder of the underlying asset receives a dividends yield 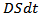 over any time interval with length
over any time interval with length  Paying dividends leads to the asset price decrease
Paying dividends leads to the asset price decrease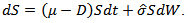 | (4.7) |
Comparing equations (3.5) and (4.7) implies that  After an elapse of time
After an elapse of time 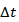 the value of the portfolio will change by the rate
the value of the portfolio will change by the rate  in view of the dividend received on h units held. Using Ito’s lemma for
in view of the dividend received on h units held. Using Ito’s lemma for  we conclude with the equation
we conclude with the equation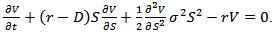 | (4.8) |
Using a new function (where
(where 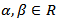 are some constants) and the transformation
are some constants) and the transformation 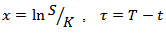 we have;
we have; 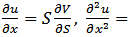
 which is substituted in (4.8) to get ;
which is substituted in (4.8) to get ;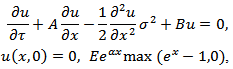 | (4.9) |
where  and
and 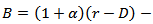
 By setting
By setting 
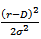
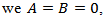 that (4.9) reduces to finding the solution of the Cauchy problem
that (4.9) reduces to finding the solution of the Cauchy problem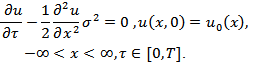 | (4.10) |
Consider a market comprising of  unit of wealth in long position (expected) and
unit of wealth in long position (expected) and  unit of the wealth in short position (actual), at time
unit of the wealth in short position (actual), at time  the market value is assumed to be
the market value is assumed to be  after an elapse the value changes by the amount and the Hausdorff measure in this case is to determine which subsets of
after an elapse the value changes by the amount and the Hausdorff measure in this case is to determine which subsets of  is the n-dimensional Euclidean space) are of zero heat capacity (that is where there is no market signal and hence market crash) with respect to the heat equation
is the n-dimensional Euclidean space) are of zero heat capacity (that is where there is no market signal and hence market crash) with respect to the heat equation 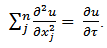 | (4.11) |
A solution  to the Cauchy problem (4.10) is given by the Green’s formula
to the Cauchy problem (4.10) is given by the Green’s formula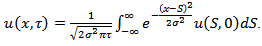 | (4.12) |
Equation (4.12) gives us the idea that the transition density of the Brownian motion in  is just the heat kernel (for
is just the heat kernel (for 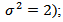
 which satisfies the heat equation (4.11). The measure zero is equivalent to the heat capacity zero on the hyper plane. It therefore follows that the solution of (4.8) is given as;
which satisfies the heat equation (4.11). The measure zero is equivalent to the heat capacity zero on the hyper plane. It therefore follows that the solution of (4.8) is given as;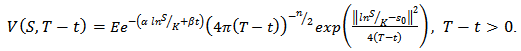 | (4.13) |
The market crash (bubble) source gives rise to a  which assigns a value to a portfolio
which assigns a value to a portfolio  to each point of
to each point of  through a generating kernel
through a generating kernel  so that on a positive market strategy
so that on a positive market strategy  on
on  is the portfolio growth rate if it is finite on a dense subset of
is the portfolio growth rate if it is finite on a dense subset of 
5. Conclusions
Equations (2.8) and (2.15) reveal that: (i) if assets returns follow a geometric Brownian motion, then the limiting distribution is gamma distribution, conversely (ii) if returns follow Weibull distribution, then it results to asymptotic power-law behavior. Furthermore the optimal strategy (2.15) depends on which in turn depends on
which in turn depends on (the singularity strength).
(the singularity strength).  as
as  and
and  (the optimal claims) increases without bound. As
(the optimal claims) increases without bound. As  and
and  decrease constantly with
decrease constantly with  Given (3.1), we have
Given (3.1), we have  (the square of the correlation coefficient) and
(the square of the correlation coefficient) and 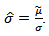 The policy is maximized by a strategy that invest as much as possible in the risky asset and the total return from this policy turns out to have stochastic dominance property as well. This continuous stochastic process can be used for modeling random behavior that evolves over time like fluctuation in an asset price and With Hausdorff measure and the heat equation via packing dimension
The policy is maximized by a strategy that invest as much as possible in the risky asset and the total return from this policy turns out to have stochastic dominance property as well. This continuous stochastic process can be used for modeling random behavior that evolves over time like fluctuation in an asset price and With Hausdorff measure and the heat equation via packing dimension  and
and  there is no market signal as it tends to zero hence the market is likely to crash at that point indicating shortfall on the wealth investment. The exact packing dimension is determined for subset of
there is no market signal as it tends to zero hence the market is likely to crash at that point indicating shortfall on the wealth investment. The exact packing dimension is determined for subset of  for which
for which 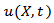 is unbounded for
is unbounded for 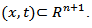 Where
Where  is n-dimensional Euclidean space. (size of the market)And for analysis of subset of B of
is n-dimensional Euclidean space. (size of the market)And for analysis of subset of B of  of Zero Hausdorff measure, it is appropriate to assume that
of Zero Hausdorff measure, it is appropriate to assume that 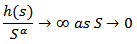 So that if
So that if  but
but  turns out to be either zero or infinity.
turns out to be either zero or infinity.
References
| [1] | Black, F. and Scholes, M. The Pricing of Option and Corporate Liabilities: Journal of Political Economy 81, (1973), 637-654. |
| [2] | Ethier, S N. and Tavare, S. The Proportional Bettor’s Return on Investments: Journal of Applied Probability 20(3), (1983), 563-573. |
| [3] | Hakansson, N.H., Optimal Investment and Consumption Strategies under Risk for a class of Utility Function: Econometrica 38(5), (1970), 587-607. |
| [4] | Hu Y. and Nualart D. Parameter Estimation for Fractional Ornstein-Uhlenbeck Process: Statistics and Probability Letters 80, (2010), 1030-1038. |
| [5] | Merton, R. C. Continuous-Time Finance: Basil Blackwell Inc., Cambridge, Ma, (1990). |
| [6] | Osu, B. O. and Adindu-Dick, J. I. Optimal Prediction of the Expected value of Assets under Fractal scaling exponent. To appear in MathSJ (2014). |
| [7] | Olkin, I., Gloser, I.J. and Derman, C. Probability models and Applications. Macmillian Publishing co, Inc. New York (1980). |
| [8] | Okoroafor, A. C. and Osu, B. O. An Empirical Optimal Selection Model. Afri. J. Math. Comp. Res. 2(1) (2009): 001-005. |
| [9] | Perold, A.F. and Sharpe, W.F., Dynamic Strategies for Asset Allocation: Reprinted from Financial Analyst Journal (1998), 16-27. |
| [10] | Taylor S.J. and Triort C., Packing Measure and its Evaluation for a Brownian path. Trans. Am. Math. Soc., 288: (1985), 679-699. |
| [11] | Thorp, E. O., Portfolio Choice and Kelly Criterion: Proceedings of the Business and Economics Section of the American Statistical Association, (1971), 215-224. |
 by the fractal dispersion of Hausdorff measure prior to market signal with constraint of a zero heat capacity, the existence of a unique solution to the associated Hausdorff is established and optimal policy is characterized. Also advocated is a procedure for locating optimal market crises signal relative to the heat equation to give an early warning.
by the fractal dispersion of Hausdorff measure prior to market signal with constraint of a zero heat capacity, the existence of a unique solution to the associated Hausdorff is established and optimal policy is characterized. Also advocated is a procedure for locating optimal market crises signal relative to the heat equation to give an early warning.
 Hence
Hence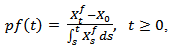
 studied by Hu, et al [4] on the continuous parametric estimation of observed fractional Ornstein-Uhlenbeck process
studied by Hu, et al [4] on the continuous parametric estimation of observed fractional Ornstein-Uhlenbeck process  defined as
defined as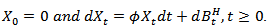
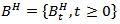 is a fractional Brownian motion with Hurst parameter
is a fractional Brownian motion with Hurst parameter 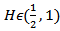 given as
given as 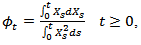
 is a measure of the wealth it takes to finance a gain. If
is a measure of the wealth it takes to finance a gain. If  is large; it means that the investor is accumulating gains at a faster rate than if it is small. Note that if we divide the numerator and the denominator by t in equation (2.1) we also interpret
is large; it means that the investor is accumulating gains at a faster rate than if it is small. Note that if we divide the numerator and the denominator by t in equation (2.1) we also interpret  as the average net gain over the average wealth level.Theorem 2.1If the returns of contingent claim
as the average net gain over the average wealth level.Theorem 2.1If the returns of contingent claim 
 follow geometric Brownian motion
follow geometric Brownian motion 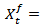
 , then the resulting distribution is Gamma distribution, that is,
, then the resulting distribution is Gamma distribution, that is, 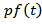
 ProofRecall that
ProofRecall that 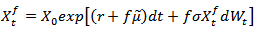 then
then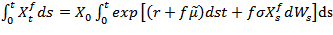
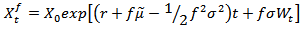
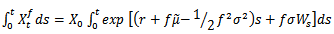
 which implies
which implies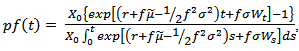 and simplifies to
and simplifies to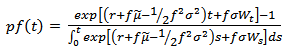
 we have that from equation (2.7) it shows that for that policy under which the total wealth is always invested in the risk-free asset is
we have that from equation (2.7) it shows that for that policy under which the total wealth is always invested in the risk-free asset is 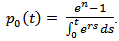 But
But  so that
so that If
If 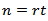 then
then  is the risk free interest rate as expected but if
is the risk free interest rate as expected but if 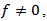 the rate of return on investment (RROI) process
the rate of return on investment (RROI) process 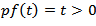 is complicated and does not yield to a simple direct analysis.NOTE: a random variable
is complicated and does not yield to a simple direct analysis.NOTE: a random variable 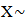 gamma
gamma  means that X is a random variable with density function
means that X is a random variable with density function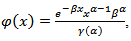 with
with  and the
and the  And for any fixed proportion that satisfies
And for any fixed proportion that satisfies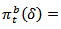
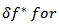 all
all  , the (RROI) process
, the (RROI) process converges
converges 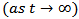 in distribution to random variable which has a gamma distribution, where
in distribution to random variable which has a gamma distribution, where 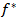 is the constant vector given by
is the constant vector given by 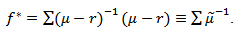 If
If  is a constant vector for all
is a constant vector for all  such a policy is called constant proportion policy which is the optimal investment policy for any interesting objective function. A constant vector is also optimal policy for other objective criteria, such as minimizing the expected time t to reach a given level of wealth as well.Specifically, as
such a policy is called constant proportion policy which is the optimal investment policy for any interesting objective function. A constant vector is also optimal policy for other objective criteria, such as minimizing the expected time t to reach a given level of wealth as well.Specifically, as 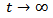 we have
we have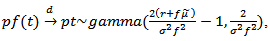
 denotes convergence in distribution.Therefore to get the expectation of
denotes convergence in distribution.Therefore to get the expectation of  we have
we have 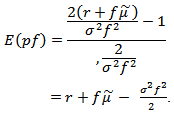
 is equal to
is equal to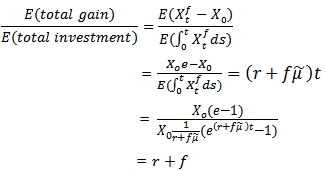
 as defined in (2.1) follow Weibull randomvariates
as defined in (2.1) follow Weibull randomvariates , then the resulting distribution
, then the resulting distribution  follows asymptotic power-law.ProofLet
follows asymptotic power-law.ProofLet 
 be distributed according to the following probability density function
be distributed according to the following probability density function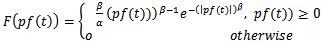
 are the mean and the shape parameters of the Weibull distribution (2.11).If
are the mean and the shape parameters of the Weibull distribution (2.11).If 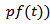 has the Weibull density function, then
has the Weibull density function, then  has the exponential density function with
has the exponential density function with  as (using the formula in [7]);
as (using the formula in [7]);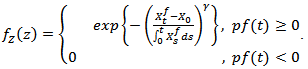
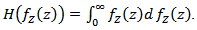
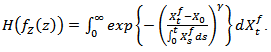
 (where
(where  is as in (2.4) or (2.6)), so that
is as in (2.4) or (2.6)), so that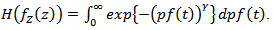 Hence the optimal strategy is the asymptotic power-law;
Hence the optimal strategy is the asymptotic power-law;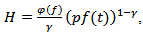
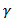 is the fractal exponent given by (see [6])
is the fractal exponent given by (see [6])  with
with  a Bessel function given as
a Bessel function given as 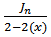 and
and 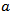 the singularity strength
the singularity strength 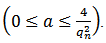
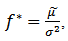
 with resulting mean
with resulting mean  for this strategy the RROI,
for this strategy the RROI,  satisfies
satisfies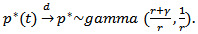
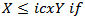
 This is equivalent to say that
This is equivalent to say that  for all increasing convex function
for all increasing convex function  and is referred to as the increasing convex ordering. We also say that (provided the expectations are finite) this is equivalent to saying that
and is referred to as the increasing convex ordering. We also say that (provided the expectations are finite) this is equivalent to saying that  for all increasing concave function
for all increasing concave function 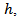 and is hence referred to as the increasing concave ordering.We let
and is hence referred to as the increasing concave ordering.We let  denote the RRIO obtained from using the policy
denote the RRIO obtained from using the policy  defined in (2.9) and let
defined in (2.9) and let  be the RROI. From any other constant proportion strategy
be the RROI. From any other constant proportion strategy  where c is an arbitrary constant, the following hold
where c is an arbitrary constant, the following hold Equation (a) is in effect for investor with greater relative risk aversion while equation (b) is in effect for an investor with less relative risk aversion. Then for a proportional strategy
Equation (a) is in effect for investor with greater relative risk aversion while equation (b) is in effect for an investor with less relative risk aversion. Then for a proportional strategy  where
where  is the optimal policy of (2.7), the relationship
is the optimal policy of (2.7), the relationship  holds if and only if C satisfies
holds if and only if C satisfies 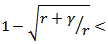
 Showing that the only type of constant proportion policy (other than
Showing that the only type of constant proportion policy (other than  for which RROI is stochastically dominated by the optimal growth policy is one that is shorting the stock to the degree required by
for which RROI is stochastically dominated by the optimal growth policy is one that is shorting the stock to the degree required by  To establish equation (2.1) in section 1 above, we have that the process
To establish equation (2.1) in section 1 above, we have that the process 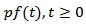 does not admit a simple direct analysis, there is a related markov process amenable to analysis which holds the key for the limiting behavior of
does not admit a simple direct analysis, there is a related markov process amenable to analysis which holds the key for the limiting behavior of  specifically the
specifically the  0 defined by
0 defined by 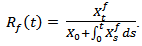
 also we will first show that the limiting behavior of
also we will first show that the limiting behavior of  is equivalent to the limiting behavior of
is equivalent to the limiting behavior of  But our interest here is to show the limiting behavior of the RROI process
But our interest here is to show the limiting behavior of the RROI process  We show that the diffusion process
We show that the diffusion process 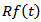 whose limiting behavior can be analyzed.Suppose that for random variable
whose limiting behavior can be analyzed.Suppose that for random variable  we have
we have 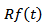
 Then for any
Then for any we have
we have 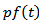
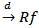
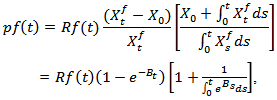
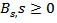 is the linear Brownian motion defined by
is the linear Brownian motion defined by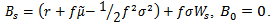 Note that
Note that  hasa positive drifts which implies that
hasa positive drifts which implies that as well as
as well as  Equation (2.1) will be completely establish if we can prove that
Equation (2.1) will be completely establish if we can prove that  for some random variable
for some random variable  with
with  Lemma 3.1: For some fixed proportion investment policy
Lemma 3.1: For some fixed proportion investment policy  the process
the process  follows the stochastic differential equation
follows the stochastic differential equation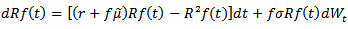
 is a temporary homogeneous diffusion process with drift function
is a temporary homogeneous diffusion process with drift function  and diffusion function
and diffusion function ProofLet
ProofLet  be the cumulative wealth investment process, also let
be the cumulative wealth investment process, also let  Since
Since  is a process of bounded variation, its Ito’s rule show that
is a process of bounded variation, its Ito’s rule show that  so applying Ito’s rule to
so applying Ito’s rule to 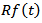 gives
gives 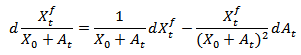 which upon substitution gives
which upon substitution gives 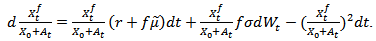
 is the notion of packing dimension due to Taylor and Triort, [10].Packing dimension is defined via the packing measure as a class φ of monotone functions h
is the notion of packing dimension due to Taylor and Triort, [10].Packing dimension is defined via the packing measure as a class φ of monotone functions h 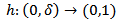 which is non decreasing, right continuous satisfying h(0+) = 0 and for which there is a constant.
which is non decreasing, right continuous satisfying h(0+) = 0 and for which there is a constant.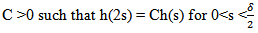
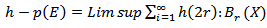
 Where
Where  denotes the open ball centered on X radius r Eq(4.2) is not an outer measure because it is not count ably Sub-additive. However it leads to an outer measure by defining
denotes the open ball centered on X radius r Eq(4.2) is not an outer measure because it is not count ably Sub-additive. However it leads to an outer measure by defining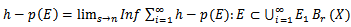
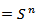 then h –p( ) on
then h –p( ) on 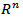 is n-dimensional Hausdorff measure. Thus to measure the Borel subset of
is n-dimensional Hausdorff measure. Thus to measure the Borel subset of  we need
we need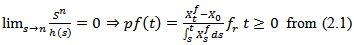
 there is a unique value of
there is a unique value of  for which the packing measure h- P(E) drops from infinity to zero.This in turn means that E is less occupied than if it were
for which the packing measure h- P(E) drops from infinity to zero.This in turn means that E is less occupied than if it were  dimensional. For
dimensional. For  We define the next Dim E as
We define the next Dim E as 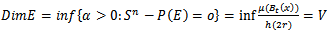
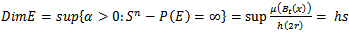
 A holder of the underlying asset receives a dividends yield
A holder of the underlying asset receives a dividends yield 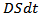 over any time interval with length
over any time interval with length  Paying dividends leads to the asset price decrease
Paying dividends leads to the asset price decrease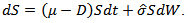
 After an elapse of time
After an elapse of time 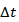 the value of the portfolio will change by the rate
the value of the portfolio will change by the rate  in view of the dividend received on h units held. Using Ito’s lemma for
in view of the dividend received on h units held. Using Ito’s lemma for  we conclude with the equation
we conclude with the equation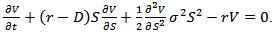
 (where
(where 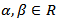 are some constants) and the transformation
are some constants) and the transformation 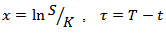 we have;
we have; 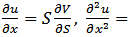
 which is substituted in (4.8) to get ;
which is substituted in (4.8) to get ;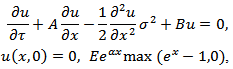
 and
and 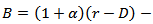
 By setting
By setting 
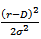
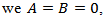 that (4.9) reduces to finding the solution of the Cauchy problem
that (4.9) reduces to finding the solution of the Cauchy problem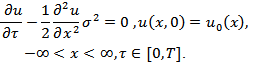
 unit of wealth in long position (expected) and
unit of wealth in long position (expected) and  unit of the wealth in short position (actual), at time
unit of the wealth in short position (actual), at time  the market value is assumed to be
the market value is assumed to be  after an elapse the value changes by the amount and the Hausdorff measure in this case is to determine which subsets of
after an elapse the value changes by the amount and the Hausdorff measure in this case is to determine which subsets of  is the n-dimensional Euclidean space) are of zero heat capacity (that is where there is no market signal and hence market crash) with respect to the heat equation
is the n-dimensional Euclidean space) are of zero heat capacity (that is where there is no market signal and hence market crash) with respect to the heat equation 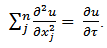
 to the Cauchy problem (4.10) is given by the Green’s formula
to the Cauchy problem (4.10) is given by the Green’s formula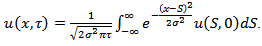
 is just the heat kernel (for
is just the heat kernel (for 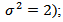
 which satisfies the heat equation (4.11). The measure zero is equivalent to the heat capacity zero on the hyper plane. It therefore follows that the solution of (4.8) is given as;
which satisfies the heat equation (4.11). The measure zero is equivalent to the heat capacity zero on the hyper plane. It therefore follows that the solution of (4.8) is given as;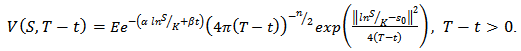
 which assigns a value to a portfolio
which assigns a value to a portfolio  to each point of
to each point of  through a generating kernel
through a generating kernel  so that on a positive market strategy
so that on a positive market strategy  on
on  is the portfolio growth rate if it is finite on a dense subset of
is the portfolio growth rate if it is finite on a dense subset of 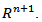
 which in turn depends on
which in turn depends on (the singularity strength).
(the singularity strength).  as
as  and
and  (the optimal claims) increases without bound. As
(the optimal claims) increases without bound. As  and
and  decrease constantly with
decrease constantly with  Given (3.1), we have
Given (3.1), we have  (the square of the correlation coefficient) and
(the square of the correlation coefficient) and 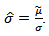 The policy is maximized by a strategy that invest as much as possible in the risky asset and the total return from this policy turns out to have stochastic dominance property as well. This continuous stochastic process can be used for modeling random behavior that evolves over time like fluctuation in an asset price and With Hausdorff measure and the heat equation via packing dimension
The policy is maximized by a strategy that invest as much as possible in the risky asset and the total return from this policy turns out to have stochastic dominance property as well. This continuous stochastic process can be used for modeling random behavior that evolves over time like fluctuation in an asset price and With Hausdorff measure and the heat equation via packing dimension  and
and  there is no market signal as it tends to zero hence the market is likely to crash at that point indicating shortfall on the wealth investment. The exact packing dimension is determined for subset of
there is no market signal as it tends to zero hence the market is likely to crash at that point indicating shortfall on the wealth investment. The exact packing dimension is determined for subset of  for which
for which  is unbounded for
is unbounded for  Where
Where  is n-dimensional Euclidean space. (size of the market)And for analysis of subset of B of
is n-dimensional Euclidean space. (size of the market)And for analysis of subset of B of  of Zero Hausdorff measure, it is appropriate to assume that
of Zero Hausdorff measure, it is appropriate to assume that  So that if
So that if  but
but  turns out to be either zero or infinity.
turns out to be either zero or infinity. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML