-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2014; 4(3): 77-85
doi:10.5923/j.am.20140403.02
Unsteady MHD Free Convection Flow Along a Vertical Plate in the Presence of Radiative Heat Flux
Nepal Chandra Roy1, Bishnu Pada Ghosh2, Litan Kumar Saha3
1Department of Mathematics, University of Dhaka, Dhaka, Bangladesh
2Department of Mathematics, Jagannath University, Dhaka, Bangladesh
3Department of Applied Mathematics, University of Dhaka, Dhaka, Bangladesh
Correspondence to: Litan Kumar Saha, Department of Applied Mathematics, University of Dhaka, Dhaka, Bangladesh.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Magnetohydrodynamic (MHD) free convection boundary layer flow of a viscous incompressible fluid along a vertical plate has been studied numerically where the effect of radiation and the surface temperature oscillation is taken into account. The governing boundary layer equations have been solved by employing two distinct methods, namely, the primitive variable method and the Keller box method. A comparison between the primitive variable method and the Keller box method is made that provides a good agreement. The effects of varying the Prandtl number, Pr, the magnetic field parameter, M, and the conduction-radiation parameter, Rd, are discussed in terms of amplitude and phase angle of skin friction for fluid having Prandtl number equals 0.1. Also we have investigated the effects of these parameters on the amplitude of oscillation of transient skin-friction and transient heat transfer and on the streamlines and isolines of temperature.
Keywords: Magnetohydrodynamics, Thermal radiation, Boundary layer, Free convection
Cite this paper: Nepal Chandra Roy, Bishnu Pada Ghosh, Litan Kumar Saha, Unsteady MHD Free Convection Flow Along a Vertical Plate in the Presence of Radiative Heat Flux, Applied Mathematics, Vol. 4 No. 3, 2014, pp. 77-85. doi: 10.5923/j.am.20140403.02.
Article Outline
1. Introduction
- The effects of thermal radiation on the free convection flows have been the focus of research interest due to many applications in space technology and in processes involving high temperatures such as nuclear power plants, gas turbines and thermal energy storage. Also the free convection flow in the presence of magnetic field is very important owing to its significant effect on the boundary layer control and on the performance of many engineering devices using electrically conducting fluids. This type of fluid flow finds application in MHD power generation, plasma studies, nuclear reactor using liquid metal coolant and geothermal energy extraction.The energy equation had lead to a highly nonlinear partial differential equation with the inclusion of radiation effects. Soundalgekar et al. [1] analyzed the radiation effects on free convection flow of a gas past a semi-infinite flat plate. Sakiadis [2] first considered the steady flow on a moving continuous flat surface and developed a numerical solution using a similarity transformation. The effect of magnetic field on the natural convection heat transfer has been studied by Sparrow and Cess [3]. Romig [4] analyzed the effect of electric and magnetic fields on the heat transfer to electrically conducting fluids. The skin friction and heat transfer on a continuous flat surface moving in a parallel free stream was studied numerically by Abdelhafez [5]. Chiam [7] delineates the solutions for steady hydromagnetic flow over a surface stretching with a power-law velocity with the distance along the surface. Hossain and Takhar [8] investigated the effect of radiation on forced and free convection flow of an optically dense viscous incompressible fluid past a heated vertical plate with uniform free stream velocity and surface temperature. The effect of radiation on the free convection heat transfer problem in the absent of magnetic field and viscous effects has been analyzed by Hossain et al. [9]. Steady free convection flow in the presence of a magnetic field past a vertical plate has investigated by a number of researchers. The problem of steady, laminar, hydromagnetic forced convection boundary-layer flow over a non-isothermal wedge with permeable surface considering the thermal radiation and heat generation or absorption effects investigated by Chamkha et al. [9]. Afify [11] studied the effects of chemical reaction on free convective flow and mass transfer of a viscous, incompressible and electrically conducting fluid over a stretching surface in the presence of a magnetic field. Duwairi [12] and Damseh et al. [13] investigated the radiation and magnetic effects on the skin friction and heat transfer for forced convection conditions. The steady nonlinear hydromagnetic flow of an incompressible, viscous and electrically conducting fluid with heat transfer over a surface of variable temperature stretching with a power-law velocity in the presence of variable transverse magnetic field has been analyzed by Devi and Thiyagarajan [14]. Ishak et al. [15] investigated the problem of mixed convection adjacent to a vertical, continuously stretching sheet in the presence of a variable magnetic field. Aydın and Kaya [16] presented numerically the effects of thermal radiation taking into account the suction or injection on a steady MHD mixed convective flows of a viscous incompressible fluid about a permeable vertical plate. Kandasamy et al. [17] studied the effects of thermophoresis and chemical reaction on MHD mixed convective heat and mass transfer past a porous wedge with variable viscosity in the presence of suction or injection. Mixed convection heat transfer about a semi-infinite inclined plate with the effects of magneto and thermal radiation analyzed by Aydin and Kaya [18]. Seth et al. [19] investigated the effects of radiation on unsteady hydromagnetic natural convection transient flow near an impulsively moving vertical flat plate with ramped wall temperature in a porous medium. Das [20] studied the effects of thermal radiation on steady two dimensional boundary layer flow of an incompressible electrically conducting fluid over a flat plate considering the partial slip at the surface of the boundary, temperature dependent fluid viscosity, variable thermal conductivity and non-uniform heat generation and absorption. Roy and Hossain [21] examined the natural convection boundary layer flow of a viscous incompressible fluid along a vertical plate taking into account the conduction–radiation interaction and surface temperature oscillations. Samad and Saha [22] investigated the two dimensional heat and mass transfer free convection flow of an MHD Non-Newtonian power-law fluid along a stretching sheet in the presence of magnetic field and assuming a simplified thermal radiation.Lighthill [23] was the first who analyzed the unsteady forced flow of a viscous incompressible fluid past a flat plate and a circular cylinder with small amplitude oscillation in free stream. The corresponding problem of unsteady free convection flow along a vertical plate with oscillating surface temperature was investigated by Nanda and Sharma [24] and Eshghy et al. [25]. Muhuri and Maiti [26] and Verma [27] have also studied the effect of oscillation of the surface temperature on the unsteady free convection from a horizontal plate.From the above literature review, we can conclude that most of the works investigated the steady behaviors of the skin friction and heat transfer for a variety of physical parameters. Even though a few works considered the unsteady problem but they used simplified models neglecting the effects of the presence of magnetic field and/or thermal radiation. In this study, we investigate the unsteady free convection flow along a vertical plate taking into account the effects of magnetic field and thermal radiation. The temperature of the plate is assumed to be oscillating about a constant mean temperature θw with a small amplitude ε as posed by Kelleher and Yang [6]. We solve the governing boundary layer equations using two distinct methods, namely, the primitive variable method and the Keller box method. Then the effects of the physical parameters such as the Prandtl number, Pr, the magnetic field parameter, M, and the conduction-radiation parameter, Rd, have been presented in terms of amplitude and phase angle of skin friction as well as transient skin-friction and heat transfer.
2. Mathematical Formulation
- Let us consider a two-dimensional unsteady laminar free convection boundary layer flow of an optically dense viscous and incompressible fluid along a vertical flat plate in the presence of magnetic field and radiative heat transfer. The surface temperature of the plate is assumed to be oscillating with small amplitude about a constant mean temperature. The plate is maintained at the surface temperature ΔT while the ambient temperature of the fluid is
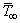 . The coordinate system and the flow configuration are shown in Figure 1.
. The coordinate system and the flow configuration are shown in Figure 1. | Figure 1. Flow configuration and coordinate system |
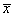 denote the distance along the plate from the leading edge,
denote the distance along the plate from the leading edge, 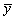 the normal distance from the plate and
the normal distance from the plate and 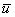 ,
,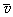 the corresponding velocity components respectively, ν the coefficient of viscosity, ρ the density of the fluid, g the acceleration due to gravity, β the coefficient of volumetric expansion,
the corresponding velocity components respectively, ν the coefficient of viscosity, ρ the density of the fluid, g the acceleration due to gravity, β the coefficient of volumetric expansion, 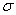 the electrical conductivity, B0 the magnetic field strength, α the thermal diffusivity, κ the thermal conductivity,
the electrical conductivity, B0 the magnetic field strength, α the thermal diffusivity, κ the thermal conductivity, 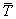 the temperature of the fluid in the boundary layer,
the temperature of the fluid in the boundary layer, 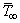 the ambient temperature of the fluid and qr represents the radiative heat flux in the
the ambient temperature of the fluid and qr represents the radiative heat flux in the 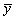 direction. Then the conservation equations for the unsteady, laminar, two-dimensional boundary layer flow under the usual Boussinesq approximation are
direction. Then the conservation equations for the unsteady, laminar, two-dimensional boundary layer flow under the usual Boussinesq approximation are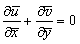 | (1) |
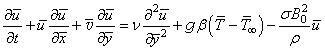 | (2) |
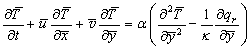 | (3) |
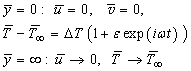 | (4) |
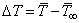 .In this study, the radiative heat flux term is simplified by using the Rosseland diffusion approximation which is valid for an optically thick fluid as follows:
.In this study, the radiative heat flux term is simplified by using the Rosseland diffusion approximation which is valid for an optically thick fluid as follows: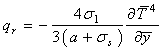 | (5) |
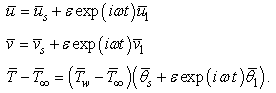 | (6) |
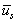 ,
, 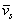 and
and 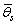 are the steady-state equations.
are the steady-state equations.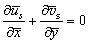 | (7) |
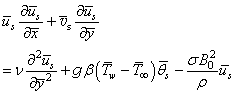 | (8) |
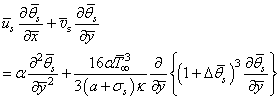 | (9) |
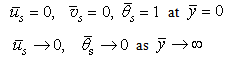 | (10) |
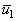 ,
, 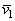 and
and 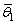 are the components of the unsteady flow, which satisfy the equations:
are the components of the unsteady flow, which satisfy the equations: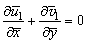 | (11) |
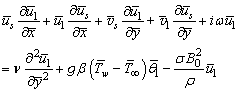 | (12) |
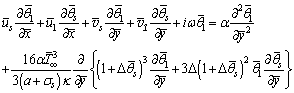 | (13) |
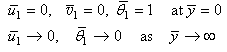 | (14) |
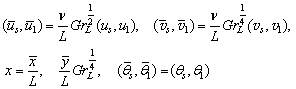 | (15) |
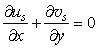 | (16) |
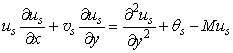 | (17) |
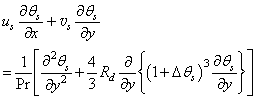 | (18) |
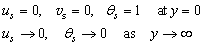 | (19) |
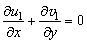 | (20) |
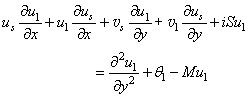 | (21) |
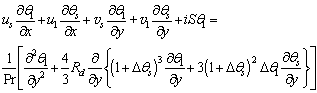 | (22) |
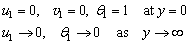 | (23) |
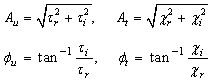 | (24) |
3. Methods of Solution
- The steady set of equations (16)-(19) have been solved by employing the primitive variable method for different values of the pertinent parameters Pr, Rd and M. The steady-state solutions are then applied in finding the solutions of unsteady equations (20)-(23), which provide the fluctuating parts of the flow and temperature fields.
3.1. Primitive-variable Formulation (PVF)
- We introduce the following group of primitive variable transformations to reduce the equations (16)-(19) and (20)-(23) into parabolic form:
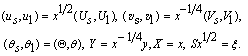 Thus from (16)-(19), we get
Thus from (16)-(19), we get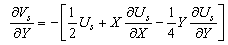 | (25) |
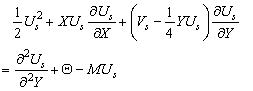 | (26) |
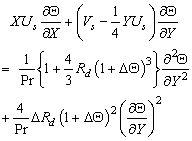 | (27) |
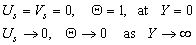 | (28) |
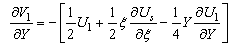 | (29) |
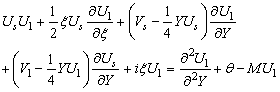 | (30) |
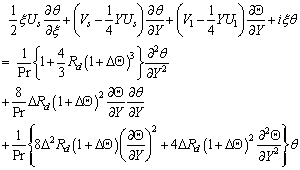 | (31) |
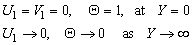 | (32) |
3.2. Stream-Function Formulation (SFF)
- We introduce the following group of well-known transformations to get the similarity equations for the steady state equations (7)-(9):
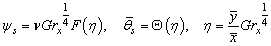 | (33) |
 satisfies the equation (7) of continuity for the steady state flow.Thus we have
satisfies the equation (7) of continuity for the steady state flow.Thus we have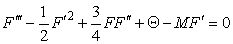 | (34) |
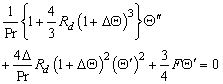 | (35) |
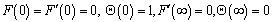 | (36) |
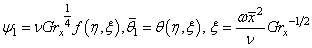 | (37) |
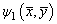 is the oscillating part of the stream function satisfying equation (11). Equation (12) and (13) then reduces to
is the oscillating part of the stream function satisfying equation (11). Equation (12) and (13) then reduces to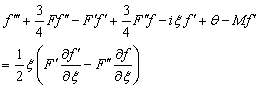 | (38) |
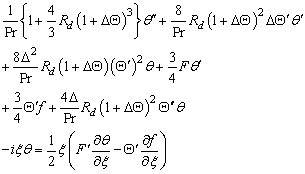 | (39) |
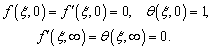 | (40) |
4. Results and Discussion
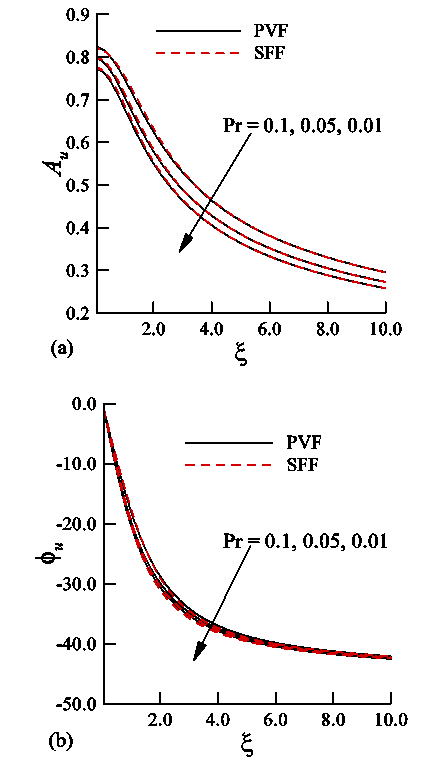
- The solutions of the equations governing the unsteady natural convection boundary layer flow with a viscous incompressible fluid along a vertical plate are obtained using the finite difference method (primitive variable formulation) and the Keller-box method (the stream-function formulation) for entire region. The results are expressed in terms of amplitude and phase angle of skin friction showing the effects of the physical parameters involved in the flow field, such as, the Prandtl number, Pr, the conduction-radiation parameter, Rd and the magnetic parameter, M while the surface temperature parameter is assumed to be fixed as θw = 1.1.A comparison between the primitive variable formulation method and the stream-function formulation method is made in Figures 2(a) and (b). The figures show that the primitive variable formulation method gives a good agreement with the stream-function formulation method. As a result, the following results will be presented only by primitive variable formulation method. In addition to, Figures 2(a) and (b) express the effects of the Prandtl number, Pr, on the amplitude and phase angle of skin friction, respectively. From both figures we observe that the amplitude of skin friction profiles decreases and the phase angle of that increases with the increase of the Prandtl number, Pr. This confirms the finding of Samanta and Guha [28] that the skin friction decreases with increasing the value of the Prandtl number.
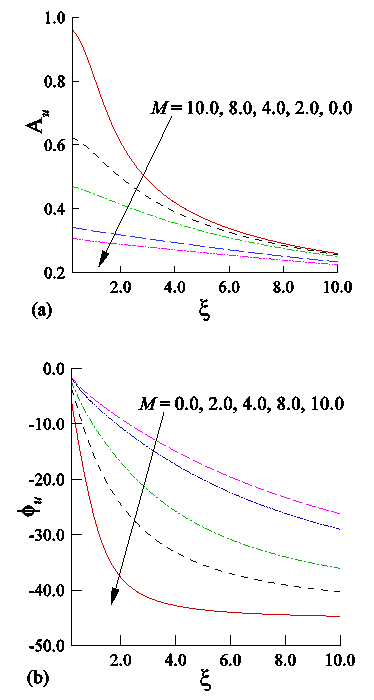 | Figure 3. Effect of magnetic field parameter (M) on (a) amplitude and (b) phase angle of skin-friction |
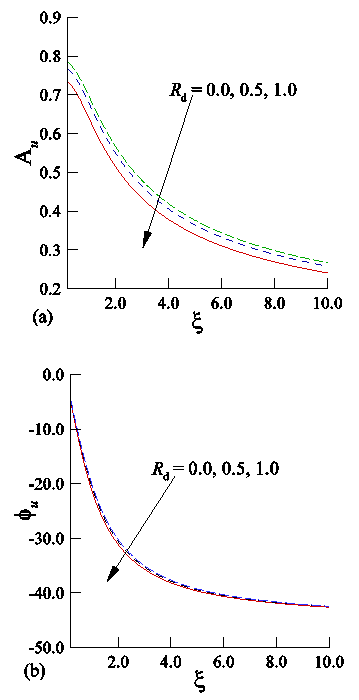 | Figure 4. Effect of conduction-radiation parameter (Rd) on (a) amplitude and (b) phase angle of skin-friction |
4.1. Effects of Different Physical Parameters on Transient Skin-friction and Heat Transfer
- Now we discuss the effects of the physical parameters, such as M, Rd, and ξ on the transient skin-friction coefficient, τ, and heat transfer coefficients, q, are measured from the following relations while Pr = 0.1.
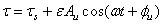 and
and 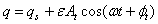 where τs and qs are respectively the steady mean skin-friction and mean heat transfer.Figures 5 and 6 show the effects of the variation of the magnetic field parameter, M, on the amplitude of oscillation of the transient skin-friction and heat transfer. From these figures, we observe that the amplitude of oscillation of the transient skin-friction decreases and that of transient heat transfer increases while M increases.
where τs and qs are respectively the steady mean skin-friction and mean heat transfer.Figures 5 and 6 show the effects of the variation of the magnetic field parameter, M, on the amplitude of oscillation of the transient skin-friction and heat transfer. From these figures, we observe that the amplitude of oscillation of the transient skin-friction decreases and that of transient heat transfer increases while M increases.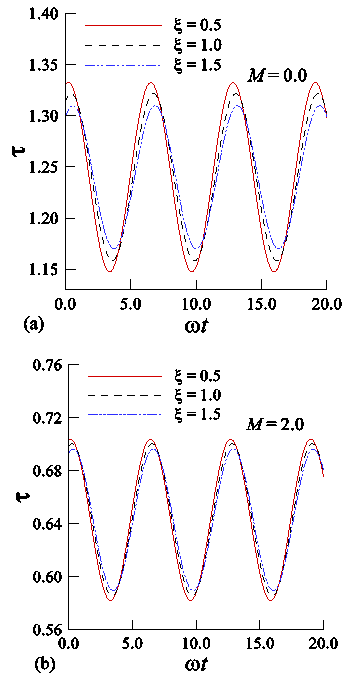 | Figure 5. Numerical values of transient skin-friction coefficient against ωt while (a) M = 0.0 and (b) M = 2.0 |
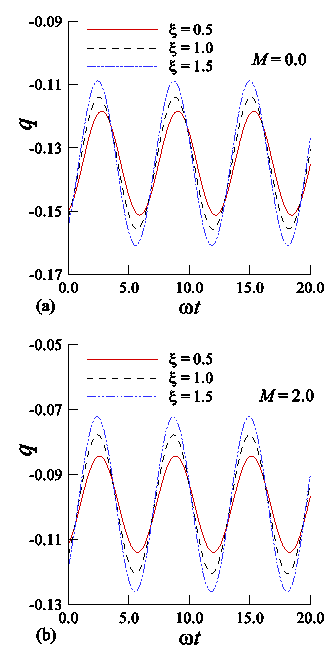 | Figure 6. Numerical values of transient heat transfer coefficient against ωt while (a) M = 0.0 and (b) M = 2.0 |
4.2. Effects of the Physical Parameters on the Streamlines and Isolines of Temperature
- Now we discuss the effects of the magnetic field parameter, M, on the streamlines and isolines of temperature in the boundary layer regimes that are shown in Figures 7(a) and (b), respectively. From the figures it is evident that both the momentum boundary layer and thermal boundary layer increase because of the increases of the magnetic field parameter, M. The reason behind these observations is that the magnetic field applied to the flow field accelerates the fluid flow as the fluid is assumed to be electrically conducting.
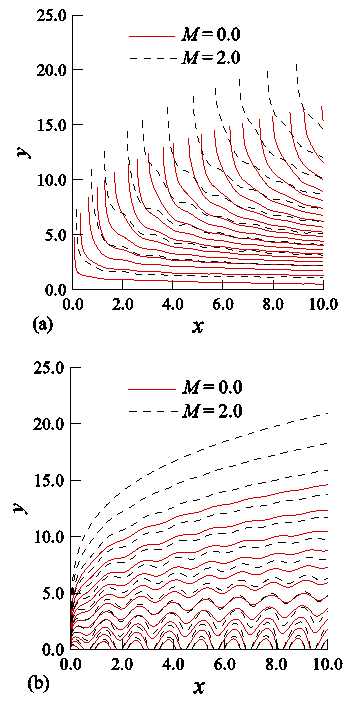 | Figure 7. The curves represent (a) streamlines and (b) isolines of temperature in the boundary layer for different values of M when τ is 5 times of x |
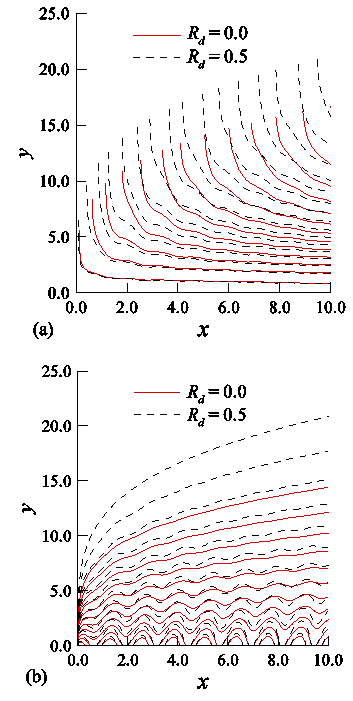 | Figure 8. The curves represent (a) streamlines and (b) isolines of temperature in the boundary layer for different values of Rd when τ is 5 times of x |
5. Conclusions
- Unsteady MHD free convection flow along a vertical plate is studied in the presence of magnetic field with thermal radiation. Two distinct methods, namely, the primitive variable formulation method and the Keller-box method are used. Detailed numerical calculations have been carried out to examine the effects of the Prandtl number, Pr, the magnetic field parameter, M, and the conduction-radiation parameter, Rd, on the amplitude and phase angle of the skin friction, transient skin friction and heat transfer as well as streamlines and isolines of temperature. Solutions obtained by primitive variable formulation method are compared with that of Keller-box method and found to be in excellent agreement.From the present analysis, it is seen that the amplitude of skin friction decreases and the phase angle of the skin friction increases with the increase of the Prandtl number, Pr and the magnetic field parameter, M. On the other hand, the amplitude of the skin friction become higher and phase angle of the skin friction decreases for lager conduction-radiation parameter. In addition, the amplitude of oscillation of the transient skin-friction decreases but that of transient heat transfer increases when the magnetic field parameter is increased. As the frequency parameter ξ increases, the amplitude of oscillation of the transient skin-friction decreases while the transient heat transfer increases.It is also found that both the momentum boundary layer and thermal boundary layer increase owing to the increase of the magnetic field parameter, M. The thicknesses of both the thermal boundary layer and momentum boundary layer increase with an increase of the conduction-radiation parameter, Rd.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML