1. Introduction

Finding a root of an algebraic and transcendental equation is always curiosity for many researchers because of its applications in many areas of science and engineering problems. Among the various existing techniques, it is well known that Newton’s method is the most popular and having quadratic convergence [1-4]. Of course, many authors have proposed new iterative scheme(s) for better and faster convergence. Some selected recent references in this regard are as follows:

He in [5] proposed new coupled iterative method for solving algebraic equations and claimed that convergence is quicker than Newton’s formula. Frontini et. al. in [6] studied about some variant of Newton’s method of third-order convergence. Because of having some mathematical mistake in [5], Luo [7] published corrected version with the discussion of some more examples and confirms that the method proposed by [5] fails to obtain expected results and no more quickly convergent than Newton’s method. Mamta et. al. in [8] proposed a new class of quadratically convergent iterative formulae and conclude that the scheme can be used as an alternative to Newton’s technique or in cases where the Newton’s technique is not successful. The same authors in [9] carried forward the discussion of [8] and derived two classes of third order multipoint methods without using second derivative and claimed about guaranteed super linear convergence of the method. Also, they claimed that the method works even if derivative of the function is either zero or very small in the vicinity of the required root. In [10], Ujevic’ has developed a method for solving nonlinear equations using specially derived quadrature rules. The author gave some numerical examples and claimed that the proposed method gives better result than the Newton’s method. Kanwar in [11] modified the method of [8] and proved that the modification converges cubically. A new family with cubic convergence by using discrete modifications is also obtained in this paper with a comment that the method is suitable in the cases where Steffensen or Newton-Steffensen method fails. In [12], Chen et. al. using [8] developed a class of formulae enclosing simple zeros of nonlinear equation and compared the method with Newton’s method. Peng et. al. in [13] proposed a new family of iterative methods without second or higher derivatives with a higher order convergence (more than three) by using Newton’s-Cotes quadrature formulas with different algebraic precision. Also, they have mentioned that in the case of multiple roots the method converges linearly only. In [14], Abu-Alshaikh et. al. proposed two algorithms by using Adomian decomposition method (ADM) [15-17]. These algorithms require two starting values that do not necessarily bracketing the root of a given nonlinear equation. However, when starting values are closed enough then the method converges faster than secant method. Another advantage of the method is that it converges to two distinct roots (one at odd iterations and other at even iterations) when the nonlinear equation has more than one root. In [18], Noor et. al. analyse new three step iterative method dependent on Adomian decomposition method [19] and claimed for third order convergence. In [20], Fang et. al. proposed new cubic local convergent iterative method and claimed about better performance of this method over Newton’s Method. Some examples are compared with [6]. In [21], Chen suggested some modifications in regula falsi method and compared some examples with regula falsi as well as Newton’s method. In [22], Kahya et. al. suggested some modifications to secant method for solving nonlinear, univariate and unconstrained optimization problems based on the development of the cubic approximation method. The performance of this method is analyzed in terms of the number of iterations in comparison with the secant methods using six test functions. In [23], Sharma suggested a new one-parameter family of second-order iteration method and shown that the method is comparable with Newton’s Method. In [24], Noor et. al. proposed two step fifth order iterative method by rewriting given nonlinear equation as a coupled system of equations and viewed the method as an improvement of the Halley’s method [25]. In [26], Chun proposed a new one-parameter family of methods comparable with [23] having second order convergence and claimed about better performance than Newton’s method. In [27], Noor et. al. suggested new three-step iterative method of fourth order convergence for solving nonlinear equation involving only first derivative of the function. Chun in [28] suggested an approach for constructing third-order modifications on Newton’s method using second - order iteration formula. Some examples are also discussed. Again, Chun in [29] presented a basic tool for deriving new higher order iterative methods that do not require the computation of the second-order or higher-order derivatives. The presented convergence analysis shows that the order of convergence of the obtained iterative methods are three or higher. In [30] Saeed et. al. suggested a new two-step and three-step iterative methods. It is shown that the three-step iterative method has fourth-order convergence. Several examples are discussed and compared with Newton’s and the method suggested by Noor et.al. [31]. In [32], Maheshwari suggested fourth order iterative method and compared the result with the results of [7, 8, 12] and others. In [33], Chun et. al. suggested new third-order and fourth-order schemes based on the method of undetermined coefficients. Singh in [34] suggested six-order variant of Newton’s Method based on contra harmonic mean for solving nonlinear equations with efficiency index 1.5651. The number of iterations taken by the proposed method is lesser than Newton’s method and the other third order variants of Newton’s method. In [35], Thukral suggested new eight order iterative method with efficiency index . Matinfar et. al. in [36] suggested two-step iterative method of six-order convergence and claimed that the method is better than Newton’s method. In [37], Shah et. al. suggested new ordinate-abscissa based iterative schemes to solve nonlinear algebraic equations which works even if

In most of the above referred papers authors have claimed that their formula can be used as an alternative to Newton’s method or in the cases where Newton’s method is not successful or fail. Also, they have claimed for higher order convergence.

In this paper new two step iterative method for solving single variable nonlinear equation is proposed. The method is having at least second order convergence and also works better than the method proposed by others who claimed for convergence higher than or equal to order two. The advantage of the method is that it also works even if, which is the limitation of the Newton-Raphson method as well as the methods suggested by [10, 18, 23, 27, 30, 32, 34-36]. The method also works even if , which is the limitation of the methods suggested by [5, 7, 20, 28]. It should be noted here that the above methods ranges the order of convergence from second to eight orders. More than fourty test functions are taken from various papers and compared with Newton’s as well as other methods. In many cases the proposed method is having faster convergence than Newton’s as well as the methods proposed by other authors.

2. Proposed Two Step Iterative Method

Let us first outline the proposed method graphically and then analytically using Taylor series expansion.

Assume that and are continuous nearer to exact root where is a simple root in some open interval I R. Let be the initial guess value sufficiently close to , then the point lie on the curve y = f (x) (Refer Figure 1). Let L₁ be a line (ordinate) joining the points (x₀, 0) and . Consider a point on line L₁ where m > 1; mR. Draw a line L₂ perpendicular to L₁ at which intersects the curve y = f(x) either at when < or when > (commonly referred as. Draw tangent to the curve at the point of intersection which intersects x-axis at x₁. The procedure discussed above can be repeated to obtain a sequence of approximations for n ≥ 1 that converges to the root .

Figure 1. The proposed method

2.1. Analytical Development of the Method

Theorem 2.1 Assume that f and there exist a number , where . Then there exists a real number > 0 such that the sequence for n ≥ 1 defined by two point iterative formulae

(1)

(2)

will converge to for the initial guess .

Proof Using Taylor series expansion and neglecting the terms containing and higher yields

(3)

Using the fact that

(4)

equation (3) with some simplification implies

(5)

Solving equation (5) for h and using the fact implies

provided

(6)

Again, using Taylor’s expansion of f(x) = 0 in power of and truncating the series after second term, implies

provided

(7)

Equation (6) shows that the continuity of are essential. Moreover, from equation (7) it is also required that () should be sufficiently close which ultimately implies should be sufficiently close.

3. Convergence Analysis

Theorem 3.1 Let f : for an open interval I. Assume that f has first, second and third derivatives in I. If f(x) has simple root at and x₀ is an initial guess sufficiently close to x^*, then the formula defined by (1) satisfies the following error equation

where

and

.

Proof

Let be the error in the n^th iteration then

(8)

Similarly, let be the error in the (n + 1)^th iteration then

(9)

Substituting (8), (9) in (1), the separate simplifications of each term using Taylor’s expansion in (1) gives

(10)

(11)

(12)

(13)

(14)

Using (10) – (14), formula (1) becomes

(15)

which implies

where

and

.

Thus, formula (1) converges linearly.

Remark It is observed from equation (15) that when m is large enough then the order of convergence of formula (1) is 3/2.

Theorem 3.2 Let f : for an open interval I. Assume that f has first, second and third derivatives in I. If f(x) has simple root at and x₀ is an initial guess sufficiently close to x^*, then the proposed method have at least quadratic convergence.

Proof By Theorem 3.1, formula (1) converges linearly and when m is large enough, the order of convergence is 3/2. Formula (2) is a Newton’s method having quadratic convergence. Hence, the order of convergence of the proposed method is at least two.

4. Discussion of Some Examples

Example 1. Consider the equation f (x) = sin(x) = 0

Table 1. Comparison of various methods for f (x) = sin(x) = 0

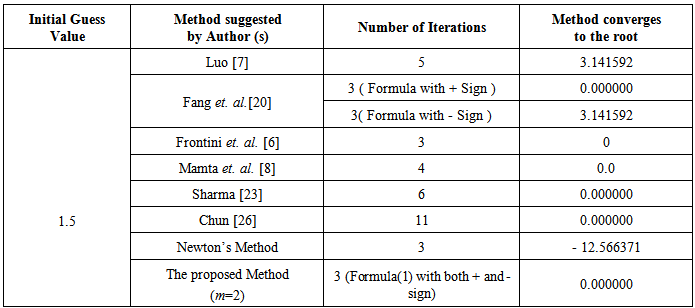
Referring to Table 1 for an initial guess value, it is interesting to note the following:

Luo [7] at 5^th iteration converges to the root 3.141592. Fang et. al. [20] considering various formulae converges to the root either 0.000000 or 3.141592 at the 3^rd iteration. Frontini et. al. [6] at 3^rd iteration converges to the root 0. Mamta et. al. [8] at the 4^th iteration converges to 0.0. Sharma [23] converges to the root 0.000000 at the 6^th iteration whereas Chun [26] converges to the same root at 11^th iteration. By Newton’s method the approximate root is - 12.566371 at the 3^rd iteration whereas the proposed method with + and - sign in the formula (1) converges to 0.000000 at 3^rd iteration as shown below in Table 2 and Table 3.

Table 2. The results for f (x) = sin(x) = 0 using + sign in formula (1) and m=2

Table 3. The results for f (x) = sin(x) = 0 using - sign in formula (1) and m=2

It is well known that, the better approximation to the exact root is always nearer to initial guess value, thus the result obtained by the proposed method as well as by Fang et. al. [20], Frontini et. al. [6], Mamta et. al. [8], Sharma [23] and Chun [26] are nearer to initial approximation , therefore, these methods works better against Luo’s method [7] and Newton’s method. But the minimum numbers of iterations are taken by the methods suggested by [20, 6] and the proposed method.

Moreover, it is interesting to note that, the proposed method using same initial guess value with two iterative directions ( from right and left ), giving same approximation to the desired root which is close to the initial guess are obtained.

Fang et. al. [20] and Frontini et. al. [6] claimed for cubic convergence for their formula whereas Mamta et. al. [8], Sharma [23] and Chun [26] claimed for quadratic convergence for their formula. So by comparison with these methods and Newton’s method, the proposed method works better. Moreover, the methods suggested by [23] and Newton’s will not work when, which is not a restriction of the proposed method. In the case of [23] the formula takes negative number under square root sign in the denominator. The proposed method is also not restricted for , which is the limitation of the methods suggested by [7] and [20].

Example 2. Consider the equation

Table 4. Comparison of various methods for

As mentioned earlier, the better approximation to the root is always nearer to initial guess value and from above Table 4 it is clear that the proposed method gives better approximation - 0.660624 with minimum number of iterations 3 or 4.

While discussing the above example, it is observed some mistake in comparison table of Mamta et. al. [8] that they have mentioned number of iterations for Newton’s method as 71 and root as -7.3182411194 which is contrary to the fact as shown in Table 4. Also, does not tend to zero.

Example 3. Consider the equation

Table 5. Comparison of various methods for

This example also shows that the proposed method works better.

Example 4. Consider the equation

Table 6. Comparison of various methods for

From the above example it is shown that the method is again quite comparable with other methods who claimed for third order convergence.

Example 5. Consider the equation

Table 7. Number of iterations by various methods

As per conclusion of Mamta et. al. [8] in applying Newton’s method to solve the equation , problems arise if the points cycle back and forth from one to another. The points cycle, each leading to other and back. It is shown that for this problem (Refer Table 7, equation number (4)) Mamta et. al. [8] took 31 iterations to converge to the root 0.0, Frontini [6] took 74 iterations to converge to the root -1 or 1 whereas the proposed method takes at the most 13 iterations to converge to the root 0.000000 or - 1.000000.

In [8], Mamta et.al. mentioned that Newton’s method diverge for this problem with initial guess value which is contradiction to the fact that it converges to the root 0.000000 at 30^th iteration (Refer Table 7). In [9], Mamta et. al. mentioned that this problem have horizontal tangents for . However, they have obtained solution 1 or -1 with number of iterations 37 ( for method (1.1) of their paper ), 38 ( for method (1.3) of their paper ) and 4 ( for method (2.12) of their paper ). The proposed method (m=2) with initial guess value converges to 0.000000 at the 13^th iteration. Also, the method with initial guess value converges to - 1.000000 at 5^th (- sign in formula(1)) and 4^th ( + sign in formula(1)) iterations. However, Halley’s method diverges in this case [9].

Again in [9], Mamta et. al. mentioned that Newton’s method with initial guess value took 59 iterations to converge to the root -1 or 1 which is contradictory to the fact they have mentioned in the conclusion that the horizontal tangents are obtained at . It is well known that at horizontal tangents, Newton’s method fails to converge.

Example 6. Consider the equation

Table 8. Root by various methods corresponding to Table 7

This example was discussed by many authors, for example, Steffensen discussed it with different initial guess values as - 3.0, - 0.5, - 0.1, 0.1 and shown that the method diverges (Refer [11]). Kanwar [11] discussed this example with the same initial guess value and shown that the method diverges in the case of - 0.1 and 0.1. Thukral [35] discussed the same example and shown that the method diverge for the initial guess value - 2.0. It should be noted here that Thukral has claimed for eight-order method. Referring to Table 9, the proposed method converges to the root - 1.207648 using initial guess value -2.0. Chun [33] also discussed the same example and compared with some third and fourth order methods. In this case for all the methods the number of iterations ranges from 4 to 7 to get the root - 1.2076478271309189270094167584 for the initial guess value -1.0. Referring to Table 9 equation (40), the proposed method (m=2) with - sign takes only 4 iterations for the root -1.207648. Matinfar et. al. [36] also discussed the same example to get the root -1.207647827130919 with initial guess value -1.0 without specifying the number of iterations. Also, [36] claimed for sixth-order convergence.

The other comparative studies are mentioned in Table 7 and Table 8. Table 7 indicates the number of iterations for various methods. Table 8 indicates the corresponding convergence to the root of the equation.

Table 9 shows the comparative studies of the proposed method with Newton’s method.

Table 9. Comparison of the Proposed Method with the Newton’s Method

5. Conclusions

The present paper proposes two step iteration schemes for finding root of a single variable nonlinear equation f (x) = 0. The following are the major conclusions:

(1) The method in formula (1) converges linearly. However, when m is large enugh then the order of convergence is 3/2. The method in formula (2) is a Newton’s method.

Hence, the present proposed two step iterative method (1) and (2) combine converges at least quadratically.

(2) The necessary condition for convergence of the formula (1) is

Also, the condition of validity of the above method is

which implies

(3) The proposed method works even if

which is the limitation of the Newton’s method as well as the methods suggested by [10, 18, 23, 27, 30, 32, 34-36].

(4) The method also works even if

,

which is the limitation of the methods suggested by [5, 7, 20, 28].

It should be noted here that the above methods in conclusion (3) and (4), ranges the order of convergence from second to eight orders.

(5) The beauty of the present method is of choosing value m which is in our control.

(6) From the above Section 4 of discussion of some examples it can also be concluded that the proposed iterative scheme gives faster convergence as compared to other quadratic, cubic and higher order convergence formulae.

(7) From Theorem 3.1, it is observed that, the proposed method have higher ( > 2 ) order of convergence when and C₃ takes negative values.

(8) From the examples discussed in Table 9, it can be concluded that the method is stable as it gives same root by considering various initial guess value in the vicinity of x^*.

(9) The formula (1) of the proposed method can also be considered as a predecessor to the Newton’s method with violation of the restriction.

(10) When both and, then the proposed method fail, this is the limitation of the method.