Abah Sunday Ojima1, Omagwu Samson1, Abah Roseline Toyin2
1Department of Mathematics, Statistics and Computer Science, Kaduna Polytechnic, Kaduna, Nigeria
2Department of Mathematics, University of Abuja, Nigeria
Correspondence to: Abah Sunday Ojima, Department of Mathematics, Statistics and Computer Science, Kaduna Polytechnic, Kaduna, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The effects of mass and radiative heat transfer on free convective flow of a viscous incompressible optically thick fluid towards a vertical surface has been investigated. The nonlinear non-dimensional, similarity-transformed boundary-layer equations governing the problem are solved using an efficient numerical method based on the fourth-order Runge-Kutta integration scheme and shooting iteration technique. Numerical calculations were carried out for different values of the various non-dimensional quantities governing the flow regime. The analysis shows that as the radiation parameter, N, increases, the temperature decreases; an increase in the prandtl number leads to a decrease in the temperature profile; a rise in the thermal Grasshof and the mass transfer number leads to increase in the velocity profile and a rise in the Schmidt number Sc leads to a decrease in the concentration profile.
Keywords:
Radiation, Free Convective Flow, Mass and Heat Transfer, Vertical Plate
Cite this paper: Abah Sunday Ojima, Omagwu Samson, Abah Roseline Toyin, Conceptual Study of the Effect of Radiation on Free Convective Flow of Mass and Heat Transfer over a Vertical Plate, Applied Mathematics, Vol. 4 No. 2, 2014, pp. 56-63. doi: 10.5923/j.am.20140402.03.
1. Introduction
The phenomenon of free or natural convection arises in fluids when temperature changes cause density variations leading to buoyancy forces acting on the fluid particles. Such flows which are driven by temperature differences abound in nature and have been studied extensively because of its applications in engineering, geophysical and astrophysical environments.When technological processes take place at higher temperatures thermal radiation heat transfer has become very important and its effects cannot be neglected (Siegel & Howel, 2001). The effect of radiation on MHD flow, heat and mass transfer become more important industrially. Many processes in engineering areas occur at high temperature and knowledge of radiation heat transfer becomes a very important for the design of the pertinent equipment. The quality of the final product depends to a great extent on the heat controlling factors, and the knowledge of radiative heat transfer in the system can lead to a desired product with sought qualities. Different researches have been forwarded to analyze the effects of thermal radiation on different flows (Shateyi and Motsa, 2009).Several people have shown considerable interest in studying the problem of free convection boundary layer flow and heat transfer as it is being affected by radiation. For example Aziz A.(2009), Vleggaar J (1977), Sivaiah M., Nagarajan A.S., Reddy P. Sreehari (2010), B. Vasu, V. Ramachandra Prasad and N. Bhaskar Reddy (2011), A. Raptis (2001), A. Raptis and C. Perdikis (2004) V.R. Prasad and N.B. Reddy (2008), M.A. Hossain, M.A. Alim, D. Rees (1999) and R.C. Bataller (2008).Hence, in the present study, we investigate the effects of mass and radiative heat transfer on free convective flow of a viscous incompressible optically thick fluid towards a vertical surface. Such a flow problem occurs in many industrial and technological applications which include the aerodynamic extrusion of plastic sheets cooling of metallic plates in a cooling bath, cooling of nuclear reactors, drawing, annealing and tinning of copper wires. Ishak, Nazar and Pop(2008) The nonlinear nondimensional, similarity- transformed boundary-layer equations governing the problem are solved using an efficient numerical method based on the fourth-order Runge-Kutta integration scheme and shooting iteration technique. Numerical calculations were carried out for different values of the various non-dimensional quantities governing the flow regime.
2. Mathematical Analysis
An unsteady one-dimensional laminar boundary layer flow of a viscous, incompressible, radiating fluid along a semi-infinite vertical plate in the presence of thermal and concentration buoyancy effects is considered, by taking the effect of viscous dissipation into account. The x′-axis is taken along the vertical infinite plate in the upward direction and the y-axis normal to the plate. Under these assumptions the Boussinesq’s approximation, for the flow field is governed by the following equations: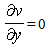 | (1.0) |
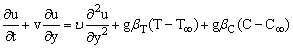 | (1.1) |
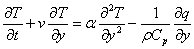 | (1.2) |
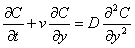 | (1.3) |
With the following the Boundary conditions,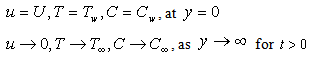 | (1.4) |
Nomenclature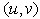 = Velocity components,
= Velocity components, 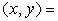 Coordinates,
Coordinates, 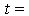 Time,
Time, 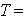 Temperature of flow,
Temperature of flow,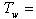 Plate surface temperature,
Plate surface temperature, 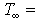 Temperature outside the flow,
Temperature outside the flow, 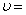 Kinematic viscosity,
Kinematic viscosity, 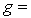 Gravity,
Gravity, 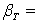 Heat transfer coefficient,
Heat transfer coefficient, 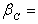 Mass transfer coefficient
Mass transfer coefficient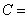 Concentration of the fluid,
Concentration of the fluid, 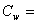 Concentration at the plate surface,
Concentration at the plate surface, 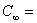 Concentration outside the flow
Concentration outside the flow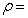 Density,
Density, 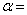 Thermal diffusion and
Thermal diffusion and 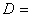 Coefficient of mass diffusion.In order to write the governing equations and the boundary condition in dimension less form, the following non- dimensional quantities are introduced
Coefficient of mass diffusion.In order to write the governing equations and the boundary condition in dimension less form, the following non- dimensional quantities are introduced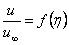 , where
, where 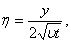
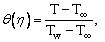

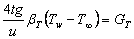 ,
, 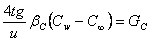
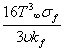 =
=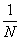 ,
, 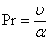 ,
, 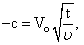
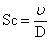
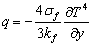 this is Rosseland approximation. (Brewster 1992)Where
this is Rosseland approximation. (Brewster 1992)Where 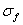 is the Stefan-Boltzman constant and
is the Stefan-Boltzman constant and 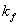 is the absorption coefficient.It should be noted that by using the Rosseland approximation the present analysis is limited to optically thick fluids.In view of the above dimensionless quantities, the governing equations is reduce to the following dimensionless form,
is the absorption coefficient.It should be noted that by using the Rosseland approximation the present analysis is limited to optically thick fluids.In view of the above dimensionless quantities, the governing equations is reduce to the following dimensionless form,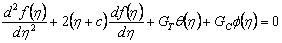 | (1.5) |
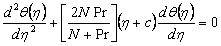 | (1.6) |
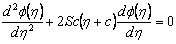 | (1.7) |
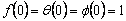 | (1.8) |
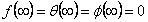 | (1.9) |
Where,c = Unsteadiness parameter, 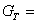 Thermal Grashof number
Thermal Grashof number 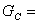 Concentration Grashof number
Concentration Grashof number 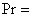 Prandlt number,
Prandlt number, 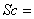 Schmindt number and
Schmindt number and 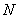 = Radiation Parameter.Numerical SolutionThe numerical solutions were obtained using an efficient numerical method based on the fourth-order Runge-Kutta integration scheme and shooting iteration technique as embedded in Maple 16. The values of the skin-friction coefficient, the local Nusselt number and the local Sherwood number are presented in table 1 and depicted graphically in Figures 1 to 8 to illustrate the influence of the various studied physical parameters.
= Radiation Parameter.Numerical SolutionThe numerical solutions were obtained using an efficient numerical method based on the fourth-order Runge-Kutta integration scheme and shooting iteration technique as embedded in Maple 16. The values of the skin-friction coefficient, the local Nusselt number and the local Sherwood number are presented in table 1 and depicted graphically in Figures 1 to 8 to illustrate the influence of the various studied physical parameters.
3. Discussion of the Results
The numerical simulation depicted by the table 1 and Figures in 1 - 8 shows that Skin-friction decreases with increasing thermal Grashof number when the Nusselt and Sherwood numbers are kept constant. The same phenomenon is observed with variation in the Solutal Grashof number. Increase in the magnitude of the Prandtl Schmidt and the radiation numbers results in corresponding increase Skin friction. In Figures 1 and 2, it is also observed that velocity varies directly with both thermal and mass Grashof number. Figure 3 demonstrates the effect of the radiation parameter on the temperature profile showing an inverse relation. The effect of the unsteadiness parameter on the velocity, temperature and concentration profile is demonstrated in Figures 4 to 6 which vary inversely with the parameter. Figure 7 shows that the temperature decreases with increase in Prandtl number. Finally Figure 8 shows that concentration varies inversely with the Schmidt number.Table 1. Numerical computations showing the Skin-friction
 the Nusselt number the Nusselt number
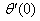 and the Sherwood number and the Sherwood number
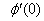 for various embedded flow parameters for various embedded flow parameters
 |
| |
|
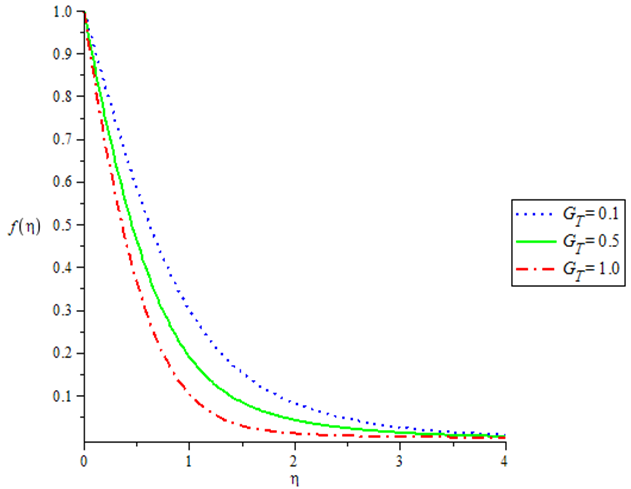 | Figure 1. Velocity profiles for various values of GT when GC = 0.1, N = 0.1, c = 0.5, Pr = 0.72, Sc = 0.24 |
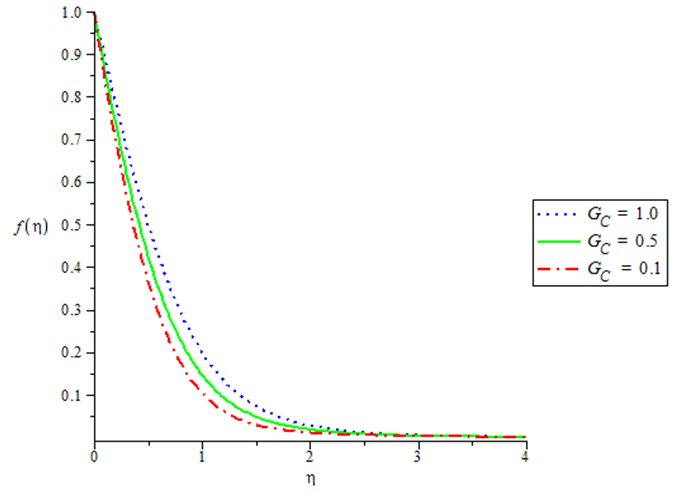 | Figure 2. Velocity profiles for various values of GC when GT = 0.1, N = 0.1, c = 0.5, Pr = 0.72, Sc = 0.24 |
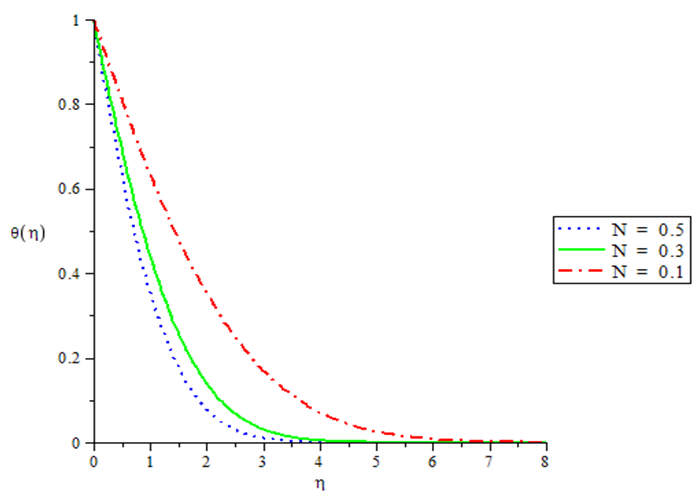 | Figure 3. Temperature profiles for various values of radiation parameter N when GT = 0.1, GC = 0.1, c = 0.5, Pr = 0.72, Sc = 0.24 |
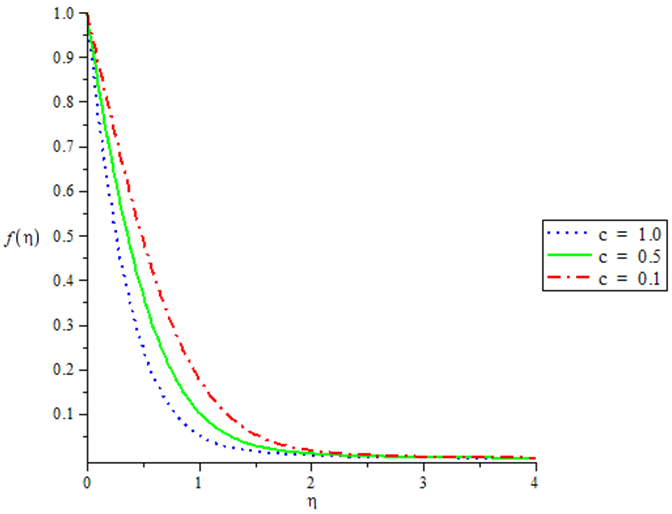 | Figure 4. Velocity profiles for various value of c when GT = 0.1, GC = 0.1, N = 0.1, Pr = 0.72, Sc = 0.24 |
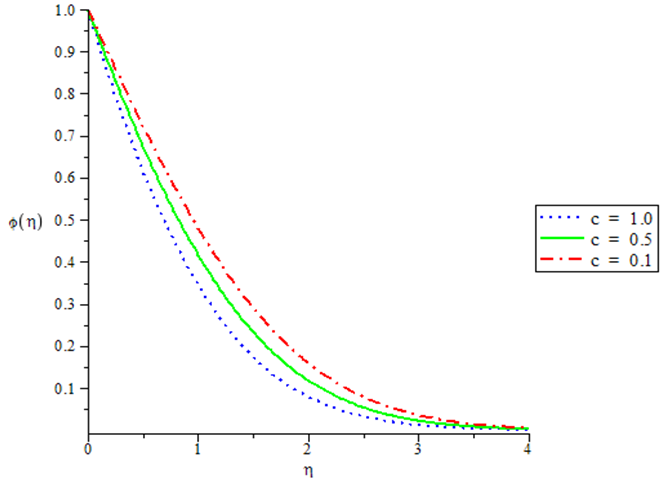 | Figure 5. Concentration profiles for various value of c when GT = 0.1, GC = 0.1, N = 0.1, Pr = 0.72, Sc = 0.24 |
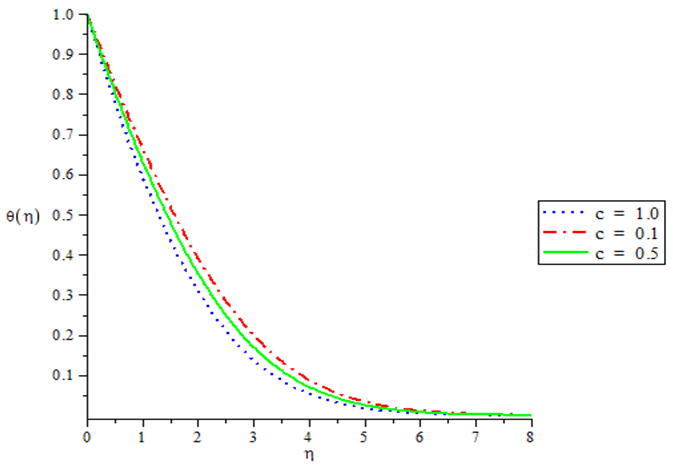 | Figure 6. Temperature profiles for various value of c when GT = 0.1, Gc = 0.1, N = 0.1, Pr = 0.72, Sc = 0.24 |
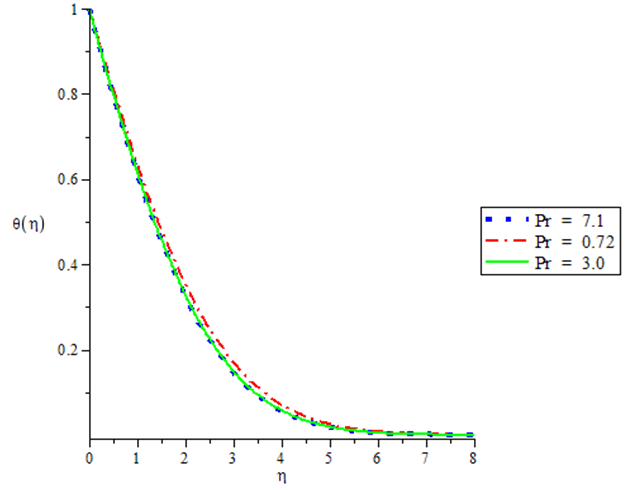 | Figure 7. Temperature profiles for various values of Prandtl number Pr when GT = 0.1, GC = 0.1, N = 0.1, c = 0.5, Sc = 0.24 |
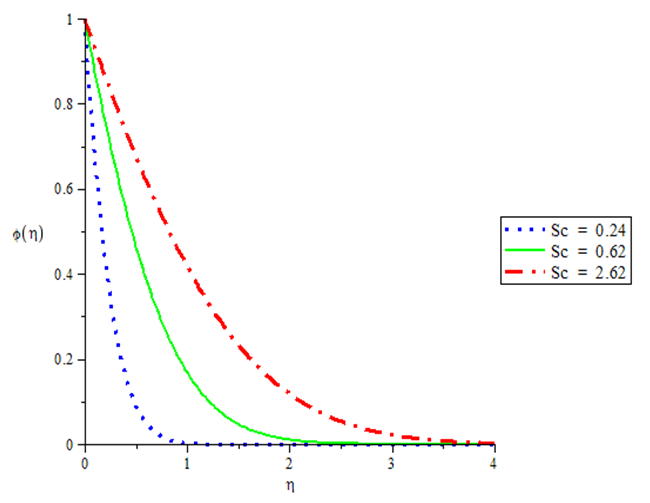 | Figure 8. Concentration profiles for various values of Schmidt number Sc when GT = 0.1, GC = 0.1, N = 0.1, c = 0.5, Pr = 0.72 |
4. Conclusions
In this paper, we have investigated numerically the effects of mass and radiative heat transfer on free convective flow of a viscous incompressible optically thick fluid towards a vertical surface, using the method of similarity transform and the resulting coupled ordinary differential equations solved using the shooting technique embedded in Maple 16.The particular conclusion drawn from this study reveals the following;l As the radiation parameter, N, increases the temperature decreases.l An increase in the Prandtl number leads to a decrease in the temperature profile.l A rise in the thermal Grashof and the mass transfer number leads to increase in the velocity profile.l A rise in the Schmidt number Sc leads to a decrease in the concentration profile.
References
| [1] | Aziz A. (2009) A Similarity Solution For Laminar Thermal Boundary Layer Over Flat Plate With Convective Surface Boundary Condition, Commun. Nonlinear Science Numerical Simulation, Vol.14, 1064-1068. |
| [2] | Sivaiah M., Nagarajan A.S., Reddy P. Sreehari (2010) Radiation Effects On MHD Free-Convection Flow Over A Vertical Plate With Heat And Mass Flux. Emirates Journal for Engineering Research, 15 (1), 35-40. |
| [3] | B. Vasu, V. Ramachandra Prasad and N. Bhaskar Reddy (2011), Radiation and Mass Transfer Effects on Transient Free Convection Flow of a Dissipative Fluid Past Semi-Infinite Vertical Plate with Uniform Heat and Mass Flux. Journal of Applied Fluid Mechanics, Vol 4 No. 1, 15-26. |
| [4] | Shateyi, S., & Motsa, S.S. (2009). Thermal Radiation Effects on Heat and Mass Transfer over an Unsteady Stretching Surface. Mathematical Problems in Engineering, Volume 2009, Article ID 965603, 13 pages doi:10.1155/2009/965603. |
| [5] | Siegel, R., & Howell, J.R. (2001). Thermal Radiation Heat Transfer, Speedy Hen, London, CA, United Kingdom, (ISBN: 1560328398 / 1-56032-839-8). |
| [6] | Vleggaar J (1977). Laminar boundary layer behavior on continuous accelerating surfaces. Chem. Eng. Sci., 32: 1517-1525. |
| [7] | A. Raptis (1998), Radiation and free convection flow through a porous medium, Int. Commun. Heat Mass Transf., 25, 289-295. |
| [8] | A. Raptis, (2001), Radiation and flow through a porous medium, J. Porous Media, 4, 271-273. |
| [9] | A. Raptis and C. Perdikis, (2004), Unsteady flow through a highly porous medium in the presence of radiation, Transport in Porous Media, 57, 171-179. |
| [10] | V.R. Prasad and N.B. Reddy (2008), Radiation effects on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a porous medium, J. Energy, Heat and Mass Transfer, 30, 57-78. |
| [11] | M.A. Hossain, M.A. Alim, D. Rees (1999), The effect of radiation on free convection from a porous vertical plate, Int. J. Heat Mass Transfer 42 181-191. |
| [12] | R.C. Bataller (2008), Radiation effects for the Blasius and Sakiadis flows with a convective surface boundary condition, Applied Mathematics and Computation 206 832-840. |
| [13] | Ishak A, Nazar R. and Pop I. (2008) Hydromagnetic Flow and Heat Transfer Adjacent To a Stretching Vertical Sheet, Heat and Mass Transfer, 44, 921-927. |

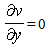
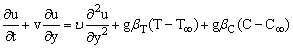
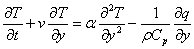
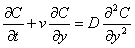
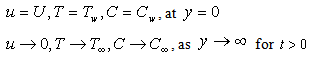
 = Velocity components,
= Velocity components, 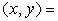 Coordinates,
Coordinates, 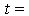 Time,
Time, 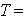 Temperature of flow,
Temperature of flow,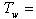 Plate surface temperature,
Plate surface temperature, 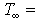 Temperature outside the flow,
Temperature outside the flow, 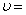 Kinematic viscosity,
Kinematic viscosity, 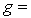 Gravity,
Gravity, 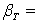 Heat transfer coefficient,
Heat transfer coefficient, 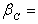 Mass transfer coefficient
Mass transfer coefficient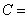 Concentration of the fluid,
Concentration of the fluid, 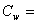 Concentration at the plate surface,
Concentration at the plate surface, 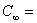 Concentration outside the flow
Concentration outside the flow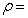 Density,
Density, 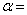 Thermal diffusion and
Thermal diffusion and 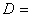 Coefficient of mass diffusion.In order to write the governing equations and the boundary condition in dimension less form, the following non- dimensional quantities are introduced
Coefficient of mass diffusion.In order to write the governing equations and the boundary condition in dimension less form, the following non- dimensional quantities are introduced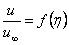 , where
, where 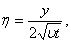
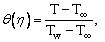

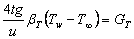 ,
, 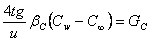
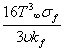 =
=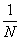 ,
, 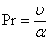 ,
, 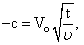
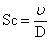
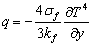 this is Rosseland approximation. (Brewster 1992)Where
this is Rosseland approximation. (Brewster 1992)Where 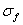 is the Stefan-Boltzman constant and
is the Stefan-Boltzman constant and 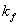 is the absorption coefficient.It should be noted that by using the Rosseland approximation the present analysis is limited to optically thick fluids.In view of the above dimensionless quantities, the governing equations is reduce to the following dimensionless form,
is the absorption coefficient.It should be noted that by using the Rosseland approximation the present analysis is limited to optically thick fluids.In view of the above dimensionless quantities, the governing equations is reduce to the following dimensionless form,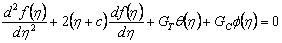
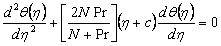
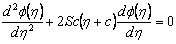
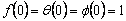
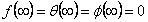
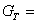 Thermal Grashof number
Thermal Grashof number 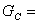 Concentration Grashof number
Concentration Grashof number 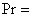 Prandlt number,
Prandlt number, 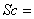 Schmindt number and
Schmindt number and 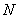 = Radiation Parameter.Numerical SolutionThe numerical solutions were obtained using an efficient numerical method based on the fourth-order Runge-Kutta integration scheme and shooting iteration technique as embedded in Maple 16. The values of the skin-friction coefficient, the local Nusselt number and the local Sherwood number are presented in table 1 and depicted graphically in Figures 1 to 8 to illustrate the influence of the various studied physical parameters.
= Radiation Parameter.Numerical SolutionThe numerical solutions were obtained using an efficient numerical method based on the fourth-order Runge-Kutta integration scheme and shooting iteration technique as embedded in Maple 16. The values of the skin-friction coefficient, the local Nusselt number and the local Sherwood number are presented in table 1 and depicted graphically in Figures 1 to 8 to illustrate the influence of the various studied physical parameters.







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML the Nusselt number
the Nusselt number 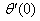 and the Sherwood number
and the Sherwood number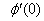 for various embedded flow parameters
for various embedded flow parameters