-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2014; 4(2): 47-55
doi:10.5923/j.am.20140402.02
Statistical Properties of the Exponentiated Generalized Inverted Exponential Distribution
Oguntunde P. E.1, Adejumo A. O.2, Balogun O. S.3
1Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria
2Department of Statistics, University of Ilorin, Kwara State, Nigeria
3Department of Statistics and Operations Research, Modibbo Adama University, Yola, Adamawa State, Nigeria
Correspondence to: Oguntunde P. E., Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
We provide another generalization of the inverted exponential distribution which serves as a competitive model and an alternative to both the generalized inverse exponential distribution and the inverse exponential distribution. The model is positively skewed and its shape could be decreasing or unimodal (depending on its parameter values). The statistical properties of the proposed model are provided and the method of Maximum Likelihood Estimation (MLE) was proposed in estimating its parameters.
Keywords: Distributions, Estimation, Exponentiated, Generalization, Inverse Exponential, Positively Skewed
Cite this paper: Oguntunde P. E., Adejumo A. O., Balogun O. S., Statistical Properties of the Exponentiated Generalized Inverted Exponential Distribution, Applied Mathematics, Vol. 4 No. 2, 2014, pp. 47-55. doi: 10.5923/j.am.20140402.02.
Article Outline
1. Introduction
- The Exponentiated distributions have been studied widely in statistics since 1995 and a number of authors have developed various classes of these distributions; Lemonte et al [1]. Mudholkar et al [2] introduced the Exponentiated Weibull distribution and since then, a number of authors have proposed and generalized many standard distributions based on the Exponentiated distributions. The Exponentiated Exponential distribution; Gupta and Kundu [3-5], The Exponentiated Gamma, Exponentiated Weibull, Exponentiated Gumbel and Exponentiated Frechet distributions; Nadarajah and Kotz [6], The Exponentiated Exponential-Geometric distribution; Silva et al [7], The Exponentiated Generalized Inverse Gaussian distribution Lemonte and Cordeiro [8], The Exponentiated Kumaraswamy distribution; Lemonte et al [1], The Exponentiated Inverted Weibull Distribution; Flaih et al [9] and the Exponentiated Generalized Inverse Weibull; Elbatal et al [10] distribution are examples of such in the literatures.The Exponentiated distribution is derived by raising the cumulative density function (cdf) of an arbitrary parent distribution to an additional non-negative parameter, say
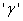 . According to Lemonte et al [1], the parameter
. According to Lemonte et al [1], the parameter 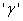 characterizes the skewness, kurtosis and tails of the resulting distribution.Let X denote a random variable from an arbitrary parent distribution G, the cumulative density function (cdf) of the resulting Exponentiated distribution is given by;
characterizes the skewness, kurtosis and tails of the resulting distribution.Let X denote a random variable from an arbitrary parent distribution G, the cumulative density function (cdf) of the resulting Exponentiated distribution is given by;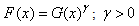 | (1) |
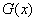 is the cdf of the parent distribution.The corresponding probability density function (pdf) is obtained by differentiating Equation (1) with respect to
is the cdf of the parent distribution.The corresponding probability density function (pdf) is obtained by differentiating Equation (1) with respect to 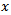 to give;
to give;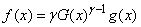 | (2) |
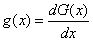 Once the cdf is obtained as in Equation (1), getting the pdf is quite simple; it only involves the knowledge of differentiation in calculus.On the other hand, Cordeiro et al [11] proposed a new class of distributions as an extension of the Exponentiated type distribution which can be widely applied in many areas of biology and engineering. Given a non-negative continuous random variable X, the cdf of the Exponentiated Generalized (EG) class of distribution is defined by;
Once the cdf is obtained as in Equation (1), getting the pdf is quite simple; it only involves the knowledge of differentiation in calculus.On the other hand, Cordeiro et al [11] proposed a new class of distributions as an extension of the Exponentiated type distribution which can be widely applied in many areas of biology and engineering. Given a non-negative continuous random variable X, the cdf of the Exponentiated Generalized (EG) class of distribution is defined by;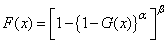 | (3) |
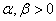 are additional shape parameters.It was noted in their research that the model in Equation (3) has a tractability advantage over the Beta Generalized family of distributions; Eugene et al [12] since Equation (3) does not involve any special function like the incomplete beta function. Equation (3) also has mild algebraic properties for simulation purposes because its quantile function takes a simple form. Hence, the corresponding pdf for Equation (3) is given by;
are additional shape parameters.It was noted in their research that the model in Equation (3) has a tractability advantage over the Beta Generalized family of distributions; Eugene et al [12] since Equation (3) does not involve any special function like the incomplete beta function. Equation (3) also has mild algebraic properties for simulation purposes because its quantile function takes a simple form. Hence, the corresponding pdf for Equation (3) is given by;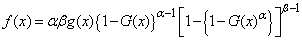 | (4) |
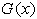 is the cdf of the baseline distribution and
is the cdf of the baseline distribution and 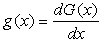 According to Cordeiro et al [11], even if the baseline pdf;
According to Cordeiro et al [11], even if the baseline pdf; 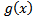 is a symmetric distribution, the resulting model in Equation (4) will not be a symmetric model because the two additional parameters
is a symmetric distribution, the resulting model in Equation (4) will not be a symmetric model because the two additional parameters  and
and  can control the tail weights and possibly add entropy to the center of the Exponentiated Generalized family of distributions.A two-parameter Generalized Inverted exponential (GIE) distribution was proposed by Abouammoh and Alshingiti [13] as a generalization of the Inverted Exponential (IE) distribution and it was shown that the Generalized Inverted Exponential distribution is better than the Inverted Exponential distribution in terms of application to a real data set when goodness of fit was assessed using the Likelihood Ratio and Kolmogorov-Smirnov tests.The probability density function of the GIE distribution is given by;
can control the tail weights and possibly add entropy to the center of the Exponentiated Generalized family of distributions.A two-parameter Generalized Inverted exponential (GIE) distribution was proposed by Abouammoh and Alshingiti [13] as a generalization of the Inverted Exponential (IE) distribution and it was shown that the Generalized Inverted Exponential distribution is better than the Inverted Exponential distribution in terms of application to a real data set when goodness of fit was assessed using the Likelihood Ratio and Kolmogorov-Smirnov tests.The probability density function of the GIE distribution is given by;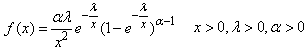 | (5) |
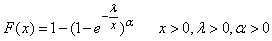 | (6) |
2. The Exponentiated Generalized Inverted Exponential Distribution
- The pdf and the cdf of the Inverted Exponential distribution are given respectively by;
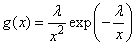 | (7) |
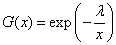 | (8) |
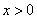 , the scale parameter
, the scale parameter 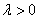 Hence, the proposed Exponentiated Generalized Inverted Exponential (EGIE) distribution is derived by substituting Equations (7) and (8) into Equation (4). Therefore, if a continuous non-negative random variable X is such that;
Hence, the proposed Exponentiated Generalized Inverted Exponential (EGIE) distribution is derived by substituting Equations (7) and (8) into Equation (4). Therefore, if a continuous non-negative random variable X is such that; 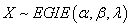 , its pdf is given by;
, its pdf is given by;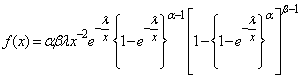 | (9) |
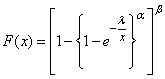 | (10) |
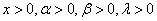
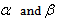 are shape parameters
are shape parameters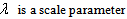 Special Cases:Let X denote a non-negative random variable with the pdf in Equation (9), some other well-known distributions are found to be sub-models of the proposed distribution. For instance;1. For
Special Cases:Let X denote a non-negative random variable with the pdf in Equation (9), some other well-known distributions are found to be sub-models of the proposed distribution. For instance;1. For 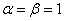 , Equation (9) reduces to the Inverse Exponential distribution which was introduced by Keller and Kamath [14]2. For
, Equation (9) reduces to the Inverse Exponential distribution which was introduced by Keller and Kamath [14]2. For 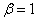 , Equation (9) reduces to the Generalized Inverse Exponential distribution which was introduced by Abouammoh and Alshingiti [13].The plots for the pdf of the proposed model at various values of parameters
, Equation (9) reduces to the Generalized Inverse Exponential distribution which was introduced by Abouammoh and Alshingiti [13].The plots for the pdf of the proposed model at various values of parameters 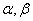 and
and 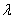 is shown in Figure 1 and Figure 2.Figure 1 shows a decreasing curve (that is, the curve decreases as the value of x increases), which means, the shape of model proposed in this article could be “decreasing”.
is shown in Figure 1 and Figure 2.Figure 1 shows a decreasing curve (that is, the curve decreases as the value of x increases), which means, the shape of model proposed in this article could be “decreasing”.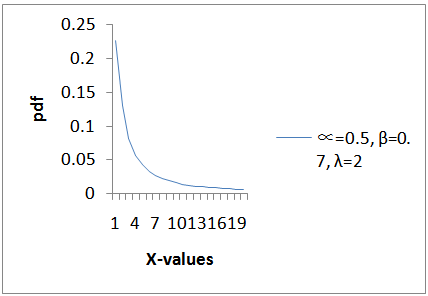 | Figure 1. Plot for the pdf at 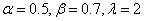 |
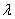 , the more spread out the curve becomes and the lower the value of
, the more spread out the curve becomes and the lower the value of 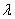 , the more compacted the curve becomes. This indicates that parameter
, the more compacted the curve becomes. This indicates that parameter 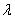 is a scale parameter.
is a scale parameter.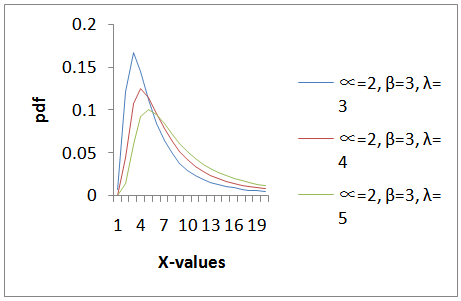 | Figure 2. Plot for the pdf at constant values of  and and  but at varying values of but at varying values of  |
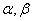 and
and 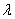 is shown in Figure 3.
is shown in Figure 3.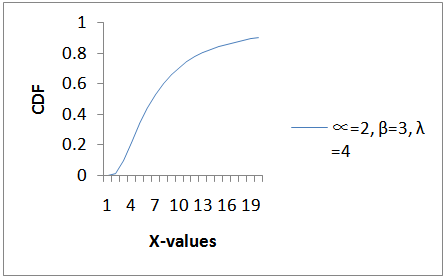 | Figure 3. Plot for the cdf at 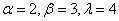 |
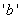 is a positive real non-integer and
is a positive real non-integer and 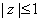 , we consider the power series expansion;
, we consider the power series expansion;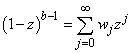 | (11) |
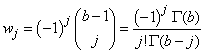 Hence, the cdf in Equation (10) can be re-written is power series representation as;
Hence, the cdf in Equation (10) can be re-written is power series representation as;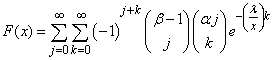 | (12) |
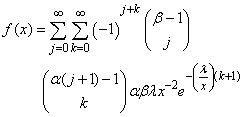 | (13) |
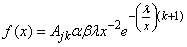 | (14) |
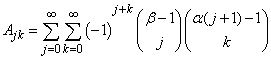 For more on the properties of the existing Exponential Models, see Anake et al [15], Oguntunde et al [16-19], Singh et al [20].
For more on the properties of the existing Exponential Models, see Anake et al [15], Oguntunde et al [16-19], Singh et al [20].3. Properties of the Proposed Model
- In this section, we present the statistical properties of the Exponentiated Generalized Inverted Exponential distribution.
3.1. Asymptotic Behavior
- We seek to investigate the behavior of the proposed model as given in Equation (9) as
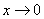 and as
and as 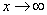 . This involves considering
. This involves considering 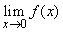 and
and 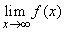 .As
.As 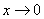 ;
;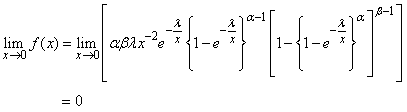 As
As 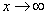 ;
;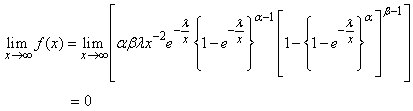 These results confirm further that the proposed distribution has a mode.
These results confirm further that the proposed distribution has a mode.3.2. Reliability Analysis
- The reliability (survival) function is given by;
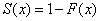 Hence, we present the reliability function of the Exponentiated Generalized Inverse Exponential distribution as;
Hence, we present the reliability function of the Exponentiated Generalized Inverse Exponential distribution as;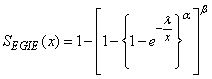 | (15) |
 units of time will survive up to
units of time will survive up to  units of time for
units of time for 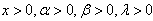 and
and 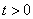 is given by;
is given by;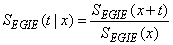
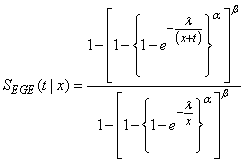 | (16) |
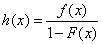 We thus present the hazard function for the proposed distribution as;
We thus present the hazard function for the proposed distribution as;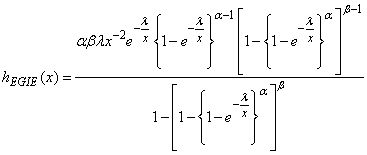 | (17) |
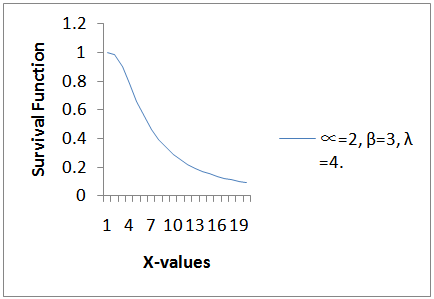 | Figure 4. Plot for the survival function at  |
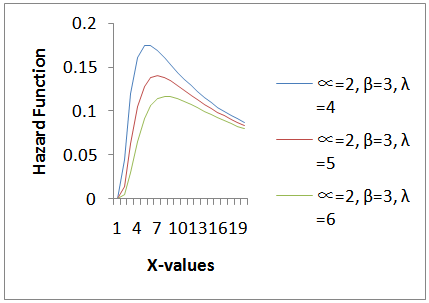 | Figure 5. Plot for the hazard function at varying values of 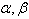 and and 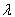 |
3.3. Quantile Function and Median
- The Quantile function is given by;
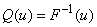 Therefore, the corresponding quantile function for the proposed model is given by;
Therefore, the corresponding quantile function for the proposed model is given by;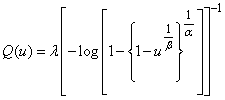 | (18) |
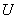 has the uniform
has the uniform 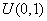 distribution. We obtain the median by substituting
distribution. We obtain the median by substituting 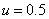 . Hence, the median of the proposed model is given by;
. Hence, the median of the proposed model is given by;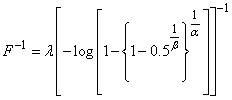 | (19) |
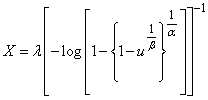 | (20) |
3.4. Moments
- The r-th moment of a continuous random variable X is given by;
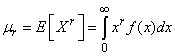 If a continuous random variable X is such that;
If a continuous random variable X is such that; 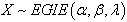 , using Equation (14),
, using Equation (14),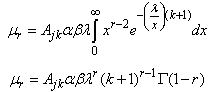 | (21) |
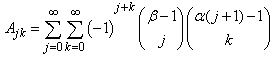
3.5. Parameter Estimation and Inference
- We estimate the parameters of the proposed distribution using the method of maximum likelihood estimation (MLE) as follows;Let
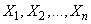 be a random sample of ‘n’ independently and identically distributed random variables each having an Exponentiated Generalized Inverse Exponential distribution defined in Equation (9), the likelihood function L is given by;
be a random sample of ‘n’ independently and identically distributed random variables each having an Exponentiated Generalized Inverse Exponential distribution defined in Equation (9), the likelihood function L is given by;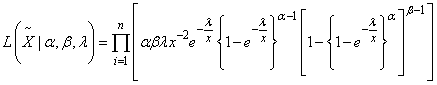 Let
Let 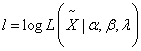
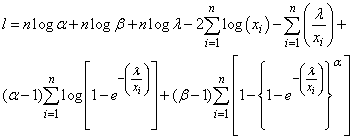 Differentiating
Differentiating 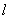 with respect to each of the parameters;
with respect to each of the parameters;  and
and 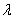 gives;
gives;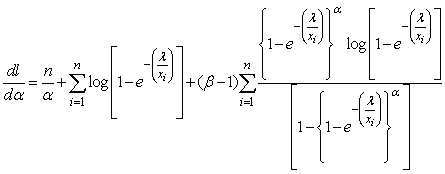 | (22) |
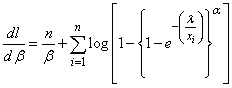 | (23) |
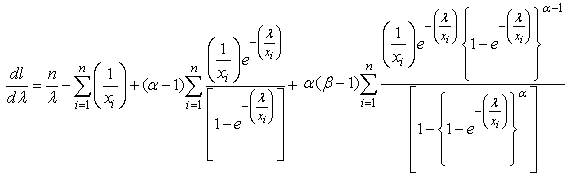 | (24) |
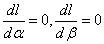 and
and 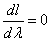 gives the maximum likelihood estimates of
gives the maximum likelihood estimates of 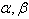 and
and 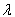 respectively.We obtain the 3 x 3 observed information matrix through;
respectively.We obtain the 3 x 3 observed information matrix through;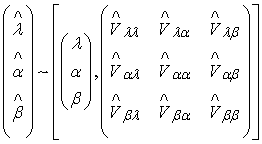
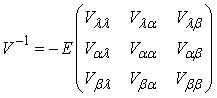 where
where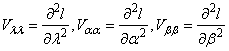
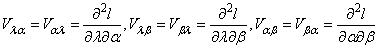 The solution of the above inverse dispersion matrix yields the asymptotic variance and covariance of the maximum likelihood estimators
The solution of the above inverse dispersion matrix yields the asymptotic variance and covariance of the maximum likelihood estimators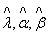 . Hence, the approximate
. Hence, the approximate 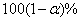 confidence intervals for
confidence intervals for 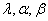 are given respectively by;
are given respectively by;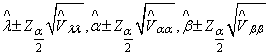 where
where 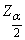 is the
is the 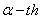 percentiles of the standard normal distribution.
percentiles of the standard normal distribution.4. Conclusions
- We define a three-parameter Exponentiated Generalized Inverted Exponential Distribution as a generalization of the Inverse Exponential distribution. The model is positively skewed, its shape could be decreasing or unimodal (depending on the values of the parameters) and it has an inverted bathtub failure rate. We provide explicit expressions for the quantile function, reliability function, failure rate and the r-th moment. The Generalized Inverse Exponential Distribution and the Inverse Exponential Distribution are found to be sub-models of the proposed model. The behavior of the failure rate shows that the proposed model is applicable in situations where the Generalized Inverse Exponential Distribution and the Inverse Exponential Distribution are used and can as well serve as an alternative to both of them. We propose the use of the new model in situations where the risk is low at the initial stage, increases with time and then decreases (for example breast cancer, bladder cancer). Further research would involve comparing the performance of this model to the Beta, Kumaraswamy, Generalized and Transmuted counterpart distributions with the aid of a real data set.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML